基于深度学习的集群式供应链应急物资需求预测研究*

薛 红，徐锐迪，王 圆，廖智峰，徐卓然

(北京工商大学计算机与信息工程学院,北京100048)

1 引言

中国是全球受到自然灾害侵袭最多的国家之一，当前，超过30种新传染病被发现，其中有一半是在中国被发现的。2002年广东省出现的SARS病毒在中国持续8个月，2019年12月湖北省武汉市发现的COVID-19直到2020年5月仍然在持续，给我国经济和人民生命财产造成不可估量的损失。当前我国应急物资的需求量大部分是根据专家的经验进行判断，由于受害程度不同，影响因素不同，只根据专家的主观性判断，会造成很大的需求误差，影响政府开展救援工作。

至今为止，国内外专家学者已经取得很多应急物资需求预测方面的研究成果。赵小柠等[1]先剖析影响应急物资需求量的有关因素，在此基础上创建以范例属性相似度为基础的后期应急物资需求序贯预测模型；刘德元等[2]假设信息不完全，将案例间的相似度结合，创建了一种预测应急物资需求量的案例模糊推理法；王兰英等[3]从应急物资需求预测的独特之处入手，构建了应用于应急物资需求量预测研究的基于模糊案例推理的预测模型；王正新等[4]将Fourier级数和GM模型结合，针对应急物资需求量小样本振荡特点，创建了以Fourier-GM为基础的应急物资需求预测模型；Liu等[5]根据模糊粗糙集理论，构建了以模糊粗糙集为基础的应急物资需求预测模型；Sheu等[6]根据大量的自然灾害案例，建立了以不完全信息为基础的应急物资需求预测模型。这些研究大部分都是相对静态的模型，并且通常以决策者的完全理性为前提，当出现相似的灾难时，决策者会更相信自己的经验，导致决策质量较低、决策效果较差。

本文从受灾地区的等级、持续时间、人数等因素进行考虑，建立基于数据流模糊C均值聚类的集群式供应链应急物资需求重要度决策算法；提出基于长短期记忆LSTM(Long Short-Term Memory)网络的集群式供应链互联大系统应急物资需求动态预测算法，提取集群式供应链子系统应急物资需求的时序特征，动态地对互联大系统的应急物资需求不确定性进行系统辨识估计，本文提出的算法不仅考虑了不同供应链之间的独特性和关联性，还考虑了受灾地区前一时刻状态对后一时刻状态的影响，即集群式供应链动态预测的概念，对于整个救援工作有着十分重大的意义。

2 集群式供应链应急物资重要度决策

2.1 集群式供应链应急物资重要度决策算法模型

因为模糊聚类算法可以更准确地展现不同模式之间的不确定关系，所以成为了近些年来学术界的研究热点，以目标函数为基础的模糊聚类算法最受青睐。本文依据模糊C均值FCM(Fuzzy C-Means)聚类算法理论，创建集群式供应链应急物资需求重要度决策算法。基于数据流模糊聚类的集群式供应链应急物资需求重要度决策算法模型为：

最小化目标函数:

(1)

其中，Jm是供应链应急物资需求重要度的目标函数，m是大于或等于1的任意实数，Uij是每个供应链子系统应急物资需求重要度评价指标Xi对于类j的隶属度，Xi为第i个拥有d个指标属性的应急物资重要度评价指标，cj为类j的聚类中心，N为拥有d个指标属性的应急物资重要度评价指标的数量，C为类的总数，‖*‖是任意一个供应链子系统应急物资需求重要度评价指标与聚类中心的相似度。

基于数据流模糊聚类的供应链应急物资需求重要度决策算法的步骤如下所示：

步骤1初始化：进行供应链应急物资需求重要度评价指标的隶属度初始化U(0)。

步骤2根据式(2)对供应链应急物资需求重要度评价指标的隶属度进行k次迭代，用U(k)计算中心向量c(k)=[cj]。

(2)

步骤3根据式(3)对供应链应急物资需求重要度评价指标的隶属度矩阵U(k)进行更新，获得U(k+1)。

(3)

步骤4根据式(4)计算数据点权值。

wi=2-λ(t-t0),i=1,2,…,N

(4)

其中，λ是衰减因子，t0是数据点到达的时刻。λ取值越大，旧数据衰减越快，对最终簇的形成影响越小。

步骤5根据式(5)计算簇权值。

(5)

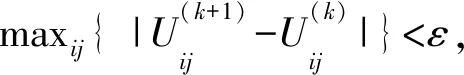
2.2 数值分析

本文研究对象是包含3条零售供应链的集群式供应链。首先将受灾情况预先设置为3个等级；然后选取集群式供应链应急物资需求预测指标体系中的3个参数——灾难级数、灾难影响时间和受灾人数，并且根据基于数据流模糊聚类的集群式供应链应急物资需求重要度决策算法进行应急物资需求重要度聚类；最后根据聚类后的簇权值判断3条供应链应急物资需求的重要度。3条供应链应急物资需求重要度决策聚类结果如图1所示。

Figure 1 Clustering results of emergency material demand importance decision of cluster supply chain图1 集群式供应链应急物资需求重要度决策聚类结果

3条供应链聚类簇权值如图2所示。

Figure 2 Cluster weights of emergency material demand importance decision of cluster supply chain图2 集群式供应链应急物资需求重要度决策聚类簇权值

根据集群式供应链应急物资需求重要度决策的聚类结果和聚类后供应链的簇权值结果，可以判断出：3条供应链应急物资需求重要度分别是一级、二级和三级。

3 集群式供应链非互联子系统应急物资需求预测

3.1 集群式供应链应急物资需求预测评估指标体系构建

在突发事件风险与大数据的情景下，本文构建的集群式供应链应急物资需求预测评估指标体系如表1所示。其中+表示影响因素与物资需求量成正比，-表示影响因素与物资需求量成反比。

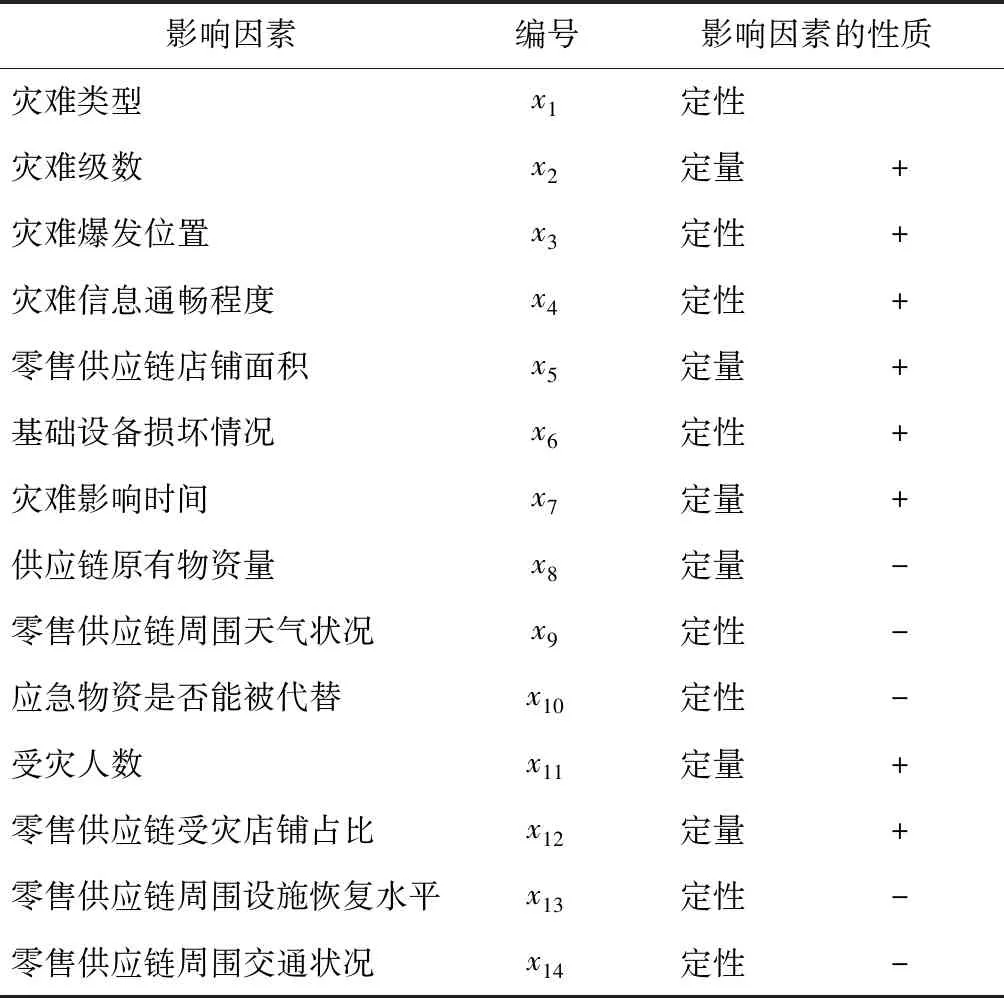
Table 1 Assessment indicator system of emergency material demand forecasting in cluster supply chain

应急物资需求预测是以剖析应急物流需求量的影响因素为先决条件的，不仅要考虑定量的影响因素还要考虑定性的影响因素。影响零售供应链应急物流需求预测的主要因素有灾难类型、灾难级数、灾难发生的地点和季节、灾难信息通畅程度、灾民数量、基础设备损坏情况、灾难影响时间和灾难发生前物资量等。

3.2 集群式供应链非互联子系统应急物资需求预测算法

本节首先运用邻域粗糙集NRS(Neighborhood Rough Set)[7]对样本指标的信息进行有效降维，改进训练样本的有效性；然后运用非线性支持向量机回归理论构建预测模型，对供应链非互联子系统的应急物资需求量进行预测。

基于邻域粗糙集的集群式供应链非互联子系统应急物资需求预测评估指标约简步骤如下所示：

步骤1∀α⊆A,根据系统应急物流需求预测样本属性指标生成分类，得到邻域关系矩阵Nα。其中A是非空有限属性集，α为其中任意长度的属性子集。

步骤2∅→red。

步骤3针对某一属性αi∈A-red，利用式(6)和式(7)求出重要度：

SIG(α,red,D)=γred∪{αi}(D)-γred(D)

(6)

(7)

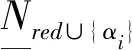
步骤4得到重要度最大的属性及其正域Posred∪{αi}(D)。

步骤5若SIG(αi,red,D)>0，red∪{αi}→red，返回步骤3；反之，转步骤6。

步骤6将被约简集合输出red，终止约简。

基于遗传算法优化支持向量机的集群式供应链非互联子系统应急物资需求预测步骤如下所示：

步骤1编码和初始种群的产生。本文采用二进制方法对支持向量机算法的惩罚因子CSVM、不敏感损失系数εSVM和核函数参数σSVM进行编码，初始种群为随机产生的。

步骤2计算适应度。采用测试样本的平均相对百分比误差MAPE作为适应度函数，基定义如式(8)所示：

(8)

其中,M表示应急物资需求预测评估指标个数；ySVMt表示实际输出值；f(xt)表示预测值。

步骤3运用交叉、变异等遗传算子对当前一代种群进行处理，产生下一代群体。

步骤4判断终止条件是否满足。如果满足，进入下一步，否则返回步骤2。

步骤5依据遗传算法优化获得支持向量机的最佳参数，采用基于支持向量机的应急物资需求预测模型进行集群式供应链非互联子系统应急物资需求预测。

3.3 数值分析

本节先运用基于邻域粗糙集[8]的应急物资需求预测评估指标约简算法对集群式供应链非互联子系统应急物资需求预测影响因素进行约简。集群式供应链非互联子系统应急物资需求预测影响因素数据如表2所示。

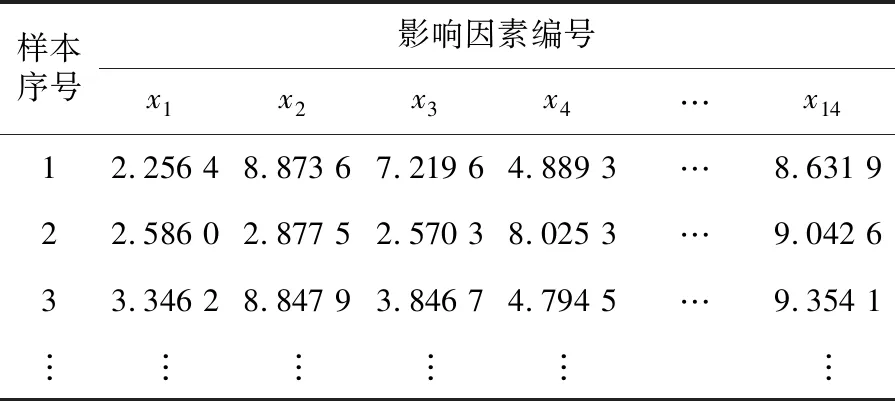
Table 2 Evaluation index data of emergency material demand prediction in cluster supply chain non-interconnected subsystem

集群式供应链非互联子系统应急物资需求预测影响因素样本数据集原有14个属性数据，经过邻域粗糙集算法约简后，最后剩下4个关键属性数据，如表3所示。

Table 3 Reduced data of emergency material demand prediction evaluation indexes for cluster supply chain non-interconnected subsystem

根据约简后的4个关键评估指标数据流，采用基于遗传算法优化支持向量机的集群式供应链非互联子系统应急物资需求预测算法进行应急物资动态需求预测，同时与原始需求数据进行比较，实验结果如图3所示。

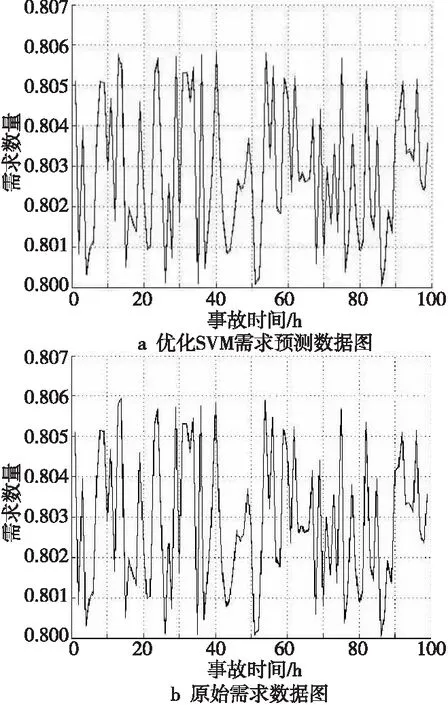
Figure 3 Comparison of raw demand data and demand forecast data图3 原始需求数据与需求预测数据对比图

本文分别采用基于邻域粗糙集(NSR)-遗传算法(GA)-支持向量机(SVM)的应急物资需求预测算法(NRS-GA-SVM)、支持向量机预测算法(SVM)[9]、BP神经网络预测算法(BP神经网络)对集群式供应链非互联子系统应急物资需求进行预测，应急物资需求预测误差如表4所示。

Table 4 Error of three prediction algorithms

通过分析平均相对误差计算结果能够发现，基于NRS-GA-SVM的应急物资需求预测算法的预测能力是最好的，其平均相对百分比误差较支持向量机的下降了约7.8435%，与BP神经网络相比下降了约14.0635%。

4 集群式供应链互联大系统应急物资需求动态预测

4.1 循环神经网络(RNN)及长短期记忆网络(LSTM)

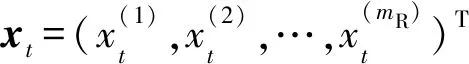
在t+1时刻，网络神经元得到的总输入为：

st+1=wyyt+wxxt

(9)

而t+1时刻神经元k的输出为：

(10)

其中，f(k)是神经元k的激活函数。

假设输入层到隐层的权重为U，隐层到输出的权重为V，自身递归的权重为W,将循环神经网络[11]在时间维度展开如图4所示。

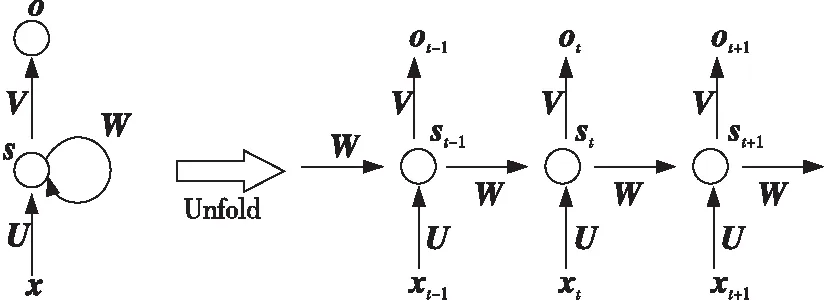
Figure 4 Expanded graph of recurrent neural network (RNN) in time dimension图4 循环神经网络(RNN)在时间维度展开图

隐层的输出为：

st=f(Uxt+Wst-1)

(11)

则输出层的输出为：

ot=g(Vst)

(12)

其中，g为激活函数。

但是，RNN有着梯度消失问题，所以需要引入LSTM[12]。LSTM的网络结构如图5所示，它的隐层依靠一个指向自身的环把此刻所处理的信息传递给下一时刻。LSTM记忆单元结构如图6所示，由记忆单元[13]的模块组成。

Figure 5 LSTM network structure图5 LSTM网络结构

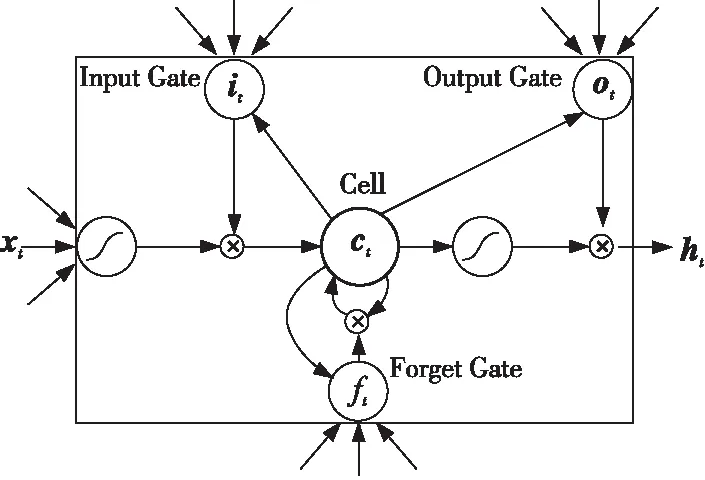
Figure 6 LSTM memory unit structure图6 LSTM记忆单元结构

当网络输入新的数据x1，并且激活函数将遗忘门ft激活时，记忆单元中上一时间段的保存数据ct-1将被清除，然后，激活函数需要将输入门it激活，新数据xt就被记忆单元ct保存。输出门ot决定是否将LSTM网络输出数据ht传输到下一个网络。

4.2 集群式供应链互联大系统应急物资需求动态预测算法模型

单条供应链应急物资需求动态预测网络结构图如图7所示。

Figure 7 Network diagram of emergency material demand dynamic prediction of cluster supply chain non-interconnected subsystem图7 集群式供应链非互联子系统应急物资需求动态预测网络图

基于长短期记忆网络的集群式供应链互联大系统应急物资需求动态预测算法模型如图8所示。

Figure 8 Network diagram of emergency material demand dynamic prediction for cluster supply chain interconnected system图8 集群式供应链互联大系统应急物资需求动态预测网络图

(13)

(14)

(15)

(16)

其中，Wxf、Wxi、Wxc、Wxo为t时刻影响集群式供应链互联大系统应急物资需求量的指标因素的权重，Whf、Whi、Whc、Who为t-1时刻影响集群式供应链互联大系统应急物资需求量的指标因素的权重，LSTM单元状态ct-1的权重为Wcf、Wci、Wco，bi、bf、bc、bo为偏置条件，向量ct-1为t-1时刻的单元状态,σ为Sigmoid函数，tanh为双曲正切函数。

集群式供应链互联大系统应急物资需求预测LSTM的t时刻隐层输出ht的计算公式为：

ht=ot×tanh(ct)

(17)

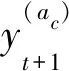
(18)

其中，ac=1,2,3;Wc1是LSTM隐层与输出层间的权重，b1是输出层的偏置。

LSTM输出是集群式供应链互联大系统应急物资需求量的特征指标因素，将其作为全连接层的输入，通过式(19)得到集群式供应链互联大系统应急物资的需求量。

(19)

最后通过式(20)计算集群式供应链互联大系统应急物资需求预测结果与真实值间的误差。

(20)

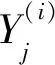
4.3 数值分析

基于长短期记忆网络的集群式供应链互联大系统应急物资需求预测算法的实验仿真结果如图9所示，图中3幅图为3条供应链的应急物资需求预测结果，其中，图9a为应急物资需求真实值图，图9b为应急物资需求预测值图。

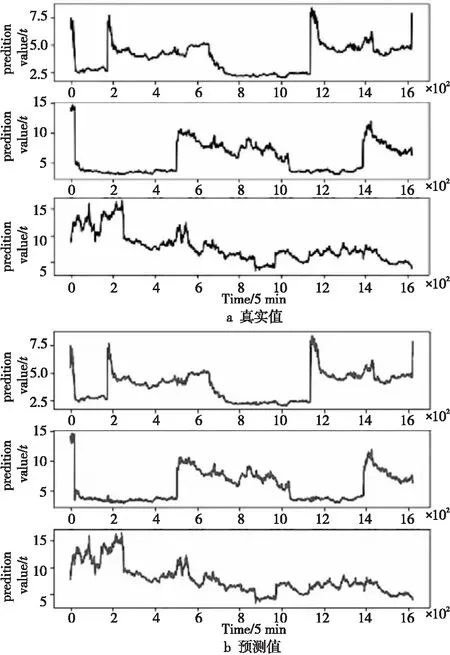
Figure 9 Prediction results of emergency material demand for cluster supply chain interconnected system图9 集群式供应链互联大系统应急物资需求预测结果

将集群式供应链互联大系统应急物资需求预测结果与基于邻域粗糙集约简、遗传算法优化支持向量机参数的集群式供应链非互联子系统应急物资需求预测结果进行比较，计算误差结果如表5所示。

Table 5 Error comparison表5 误差比较表

通过比较基于长短期记忆网络的集群式供应链互联大系统应急物资预测算法与基于NRS-GA-SVM的集群式供应链非互联大系统应急物资需求预测算法的应急物资预测结果可知，基于长短期记忆网络的集群式供应链互联大系统应急物资需求预测算法的预测精度高于基于NRS-GA-SVM的集群式供应链非互联大系统应急物资需求预测算法。

5 结束语

突发事件所影响的地区地域广袤，受灾地区通常会有多条供应链[14]，它们既相互独立又存在紧密的联系。在预测集群式供应链应急物资需求时，即要考虑单条子供应链的特征，还要考虑不同供应链之间的相互影响，因此从集群式供应链的角度开展应急物资需求预测研究是必要的。此外，突发事件对受灾地区的影响时间较长，若想在突发事件发生后最大程度地减小损失，除了需要考虑集群式供应链所在地区的受灾程度外，还要考虑受灾地区前一时刻灾情对受灾地区后一时刻灾情的影响，提高应急物资需求预测的精确水平，减少灾民的生命财产损失。因此，集群式供应链应急物资需求动态预测研究有着非常重要的理论意义和很高的应用价值。