LCL型并网逆变器的网压滤波前馈控制策略
(四川大学电气工程学院,四川 成都 610065)
LCL型并网逆变器是连接分布式发电系统与公共电网之间的核心设备,其入网电流质量问题受到国内外专家和学者的关注[1-4]。目前,广泛使用的电网电压比例前馈策略虽然能显著增强LCL型并网逆变器的谐波抗扰能力[5],保证了入网电流质量,但在拥有丰富背景谐波和电网阻抗宽范围变化的弱电网下,该策略的稳定性较差,易受来自电网阻抗变化的影响,进而大幅放大入网电流中的谐波分量[6]。国家电网已明确规定,分布式发电系统需满足在最小短路比10所对应的电网阻抗下稳定运行[7],因此,提高网压比例前馈策略在弱电网下的适应性已成为近年来研究的热点,国内外学者对此已作出相关研究。
文献[8-9]提出了基于电网阻抗测量技术的自适应控制策略,在内环中引入了自适应相位补偿环节,用于消除稳定性下降的不利影响,但是该策略的补偿效果依赖于阻抗测量技术的精准度,并且阻抗测量技术的应用会一定程度地恶化入网电流质量,其实际应用价值有限。文献[10]提出一种基于加权系数的网压比例前馈策略,实现方式简单有效,但该方法是以牺牲一定的谐波抗扰能力来提升其稳定性的,系统适应性的提升空间有限。文献[11-12]采用构建虚拟阻抗的方法来实现稳定性的提升,但是其构建函数引入了微分项,将严重放大入网电流中高频谐波,且在实际工程中,微分环节也难以实现。
本文首先推导了LCL型并网逆变器的输出阻抗模型,明晰了网压比例前馈对弱电网的适应性;之后提出一种基于多二阶滤波器的网压前馈控制策略,详细分析了该策略的实现方式,滤波器参数设计,谐波抗扰能力以及应对电网阻抗宽范围变化的稳定性;同时与现有策略以及传统策略进行了对比。对比结果表明,该策略对弱电网同样拥有优越的适应性,可在恶劣的弱电网条件下输出质量良好的入网电流,无需复杂的电网阻抗测量技术,系统计算量更小,并且,引入的新环节也无微分项,无放大高频谐波的副作用。
1 弱电网下LCL型并网逆变器的输出阻抗模型
含网压比例前馈策略的单相LCL型并网逆变器的模型结构图如图1所示。
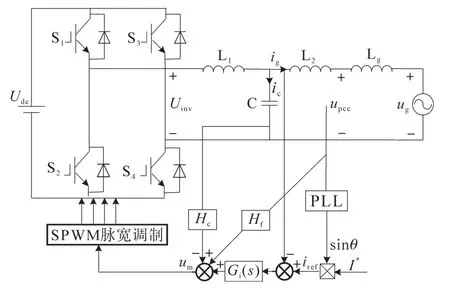
图1 含网压比例前馈的LCL型并网逆变器模型结构图Fig.1 Model structure diagram of LCL-type grid-connected inverters with grid voltage proportional feedforward
图 1 中,Udc为直流侧电压源;S1,S2,S3,S4为IGBT开关管;Uinv为逆变器输出电压;L1,C,L2分别为LCL滤波器的电感电容元件;ic,ig分别为逆变器电容电流以及入网电流;upcc为公共耦合点电压;Lg为弱电网下呈感性的电网阻抗;ug为电网电压;I*为指令电流幅值;upcc经过锁相环(phase locked loop,PLL)得出电网电压相位 θ,与 I*结合后形成指令电流iref;Gi(s)为电流控制器;Hc为电容电流采样系数,用于抑制LCL滤波器的谐振;Hf为网压比例前馈系数;um为控制环路得出的调制波,um经过正弦脉宽调制后,将占空比信号传递至4个开关管,从而控制开关管的工作。
图2为LCL型并网逆变器的结构控制框图。

图2 LCL型并网逆变器的控制框图Fig.2 Control block diagram of LCL-type grid-connected inverters
图2中,Gkd(s)为数字控制下零阶保持器,一拍计算延时,采样开关以及脉宽调制增益系数Kpwm共同构成的延时环节,其表达式如下式所示:

式中:Ts为采样周期。
Gkd(s)结构如图3所示,其中,Kpwm通常等效为下式[13]:

式中:Utri为三角载波幅值。
另外,图2中网压比例前馈系数Hf的表达式如下式所示:

电流控制器Gi(s)采用准比例谐振控制器,实现对基波频率信号的良好跟踪,Gi(s)的传递函数如下式所示:
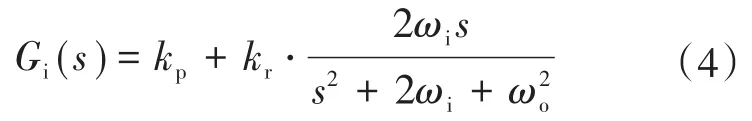
式中:kp为控制器的比例系数;kr为控制器的基波增益系数;ωi为控制器带宽调整参数;ωo为基波信号的角频率。
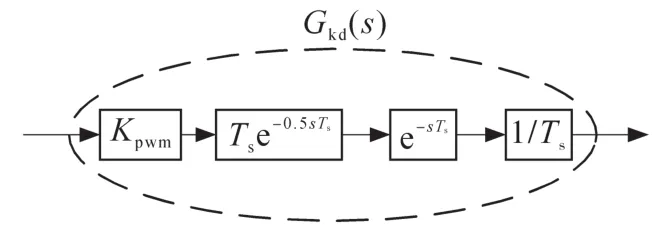
图3 延时环节Gkd(s)的结构图Fig.3 Structure diagram of delay link Gkd(s)
并网逆变器控制框图如图4所示。
对图2进行等效变换,将网压反馈点前移至Gi(s)的输入端,则图2可进一步等效为图4a。其中,Gx1(s)与Gx2(s)的表达式分别如下所示:
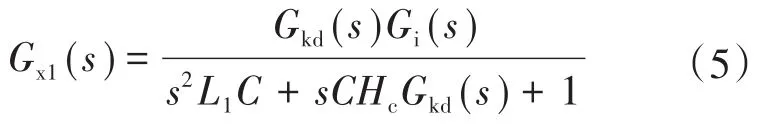
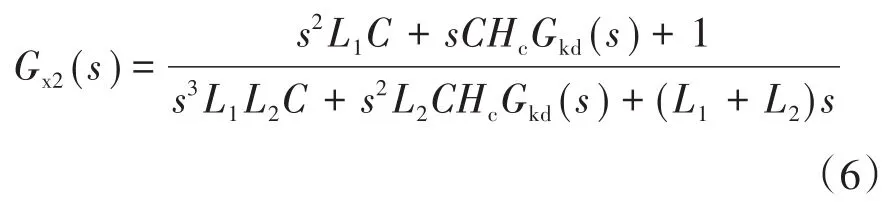
由图4a可得出系统的环路增益T(s)为
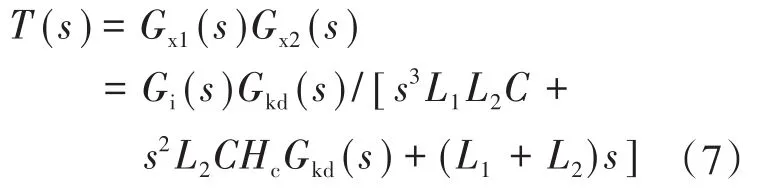
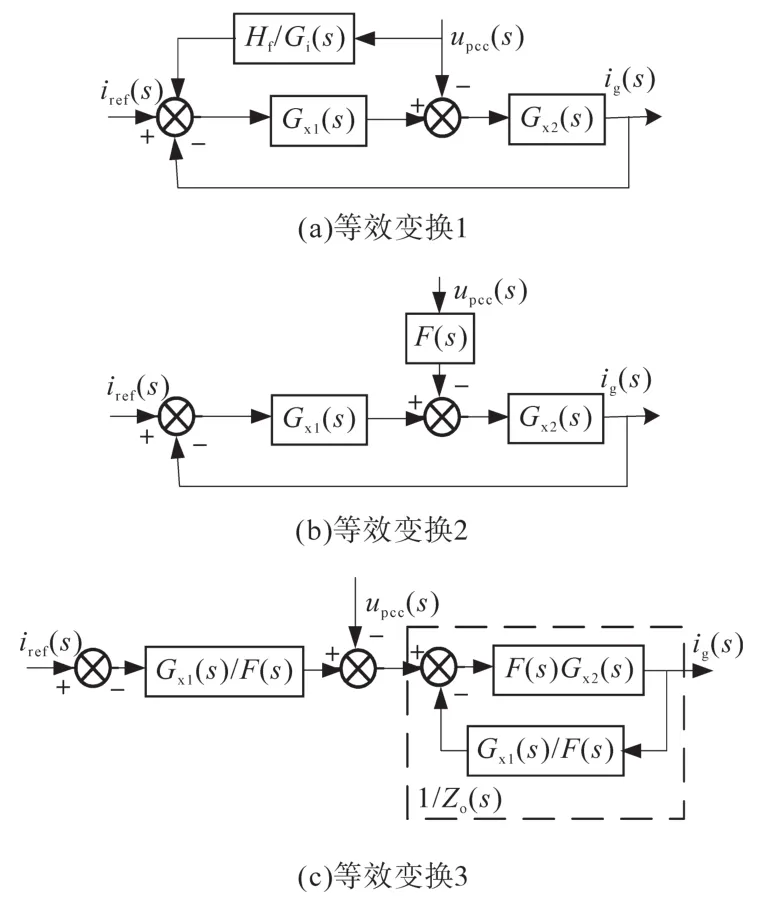
图4 并网逆变器控制框图的等效变换Fig.4 Equivalent transformation of control block diagram of grid-connected inverters
将图4a的网压前馈点提前至Gx1(s)输入端,并合并upcc(s)的所有输入项,可进一步得到图4b。其中,F(s)为电网电压扰动函数,表达式如下式所示:

式(8)反映了upcc点的扰动对并网逆变器的影响程度。
进一步将图4b中入网电流ig(s)的反馈端前移至Gx2(s)的输入端,同时把F(s)移动至Gx2(s)的输入端,可得到图4c所示的等效框图。其中,Zo(s)表示并网逆变器的输出阻抗,其表达式如下:
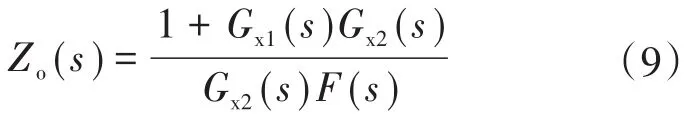
根据图4c,可建立LCL型并网逆变器的输出阻抗模型图,如图5所示。
图5中,ieq(s)为并网逆变器的等效电流源,同时把弱电网等效为电压源ug(s)与电网阻抗Zg(s)串联的电路,Zg(s)与ieq(s)的表达式如下式所示:
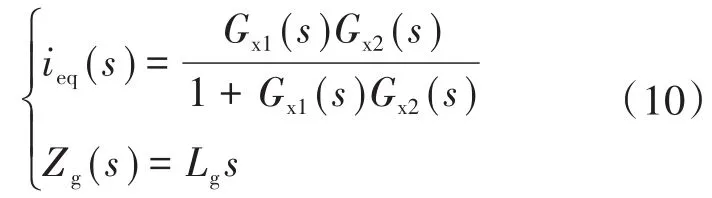

图5 并网逆变器的输出阻抗模型图Fig.5 Output impedance model diagram of grid-connected inverters
根据叠加定理,可推导出图5的电路关系式如下:
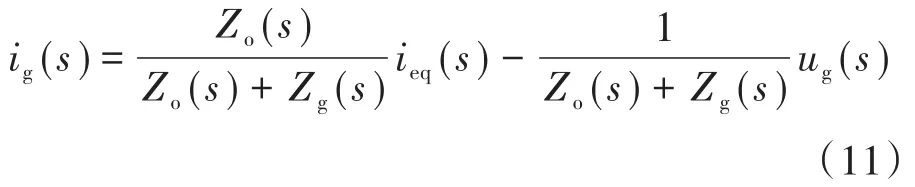
由式(11)可知,并网逆变器若想抑制来自电网ug(s)的谐波干扰,必须提高分母上Zo(s)+Zg(s)的模值,其中,Zg(s)为一阶微分项,相位始终为90°,而且其阻抗值会随着频率的增大而增大,所以必然存在某一交截频率fi处,Zo(2πfi)的模值等于Zg(2πfi)的模值,若在该交截频率fi处,两者的相位相反,即Zg(2πfi)+Zo(2πfi)=0,根据式(11),则电网背景谐波将被无穷放大。
综上所述,若要求并网逆变器系统拥有良好的谐波抗扰能力和稳定性,需要其输出阻抗Zo(s)在背景谐波频率处拥有高阻抗幅值,在阻抗交截频率fi处拥有充足的相位裕度PM,一般工程要求PM>40°,PM的表达式如下:
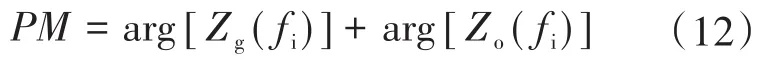
2 弱电网下网压比例前馈策略的适应性分析
2.1 系统谐波抗扰能力分析
图6为网压比例前馈策略下电网电压扰动函数F(s)的波德图。由图6不难发现,比例前馈策略在小于fu的频段里,皆可实现电网电压扰动的抑制,且频率越低,抑制效果越好,故网压比例前馈策略基本可以消除电网中低次谐波的干扰,但是受系统中固有的延时环节Gkd(s)的影响,导致系统相位随频率的增加不断滞后,影响了网压比例前馈策略的谐波抑制效果,甚至在大于fu的频段里,网压比例前馈还放大了电网中的高次谐波,但通常来说,实际电网当中高次谐波含量较少,所以放大效果可忽略不计。综上所述,网压比例前馈在谐波抗扰能力上表现良好,对电网中含量较高的低频奇次谐波有着很好的抑制效果。
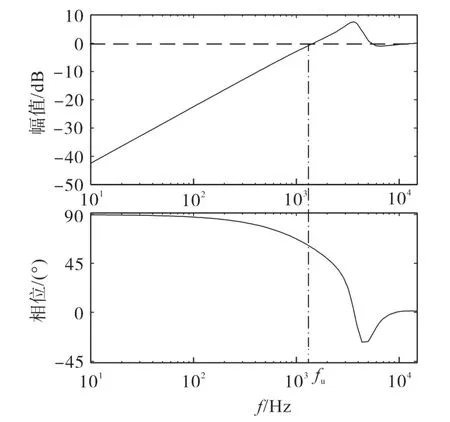
图6 电网电压扰动函数F(s)的波德图Fig.6 Bode diagram of grid-voltage disturbance function F(s)
2.2 系统应对电网阻抗变化的稳定性分析
图7为网压比例前馈策略下并网逆变器输出阻抗Zo(s)的波德图。同样由图7可知,网压比例前馈策略能显著提高并网逆变器输出阻抗的模值,但是却大幅降低了其稳定性,输出阻抗Zo(s)在低频段处的相位基本低于-90°,导致该策略难以适应弱电网下宽范围变化的电网阻抗,当电网阻抗较小为2.5 mH时,在交截频率f2处,逆变器拥有较好的相位裕度,但是随着电网阻抗的增大,PM将下降至3.2°,不能满足工程要求的相位裕度标准,导致f1频率附近的电网背景谐波大幅放大,恶化了入网电流质量,故有必要进一步改善网压比例前馈策略在弱电网下的稳定性。
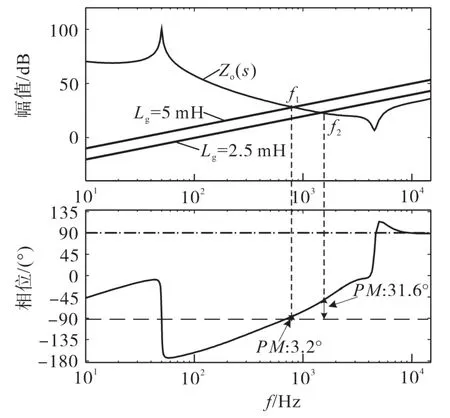
图7 输出阻抗Zo(s)的波德图Fig.7 Bode diagram of output impedance Zo(s)
3 提出基于多二阶滤波器的网压前馈控制策略
3.1 网压滤波前馈控制策略的实现原理
考虑到网压比例前馈策略是牺牲系统在弱电网下的稳定性来提升中低频段的谐波抗扰能力,但是在实际电网当中,主要存在13次以下的谐波分量,故网压比例前馈策略无需实现整个中低频段的谐波抑制,只需对特定次谐波进行抑制即可,而其余频段不引入网压反馈,便可恢复系统在中频段的稳定性,故本文可利用多个二阶滤波器来提取前馈通道上特定次谐波信号进行网压反馈,而对其余频段的信号不进行提取和反馈。改进后的系统框图如图8所示。
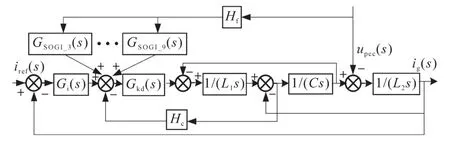
图8 改进后LCL型并网逆变器的控制框图Fig.8 Control block diagram of the improved LCL-type grid-connected inverters
3.2 二阶滤波器的参数设计
图8中,GSOGI_n(s)为二阶滤波器,其实质上是带通的二阶广义积分器,能实现特定次频率信号的提取,其表达式如下式所示:
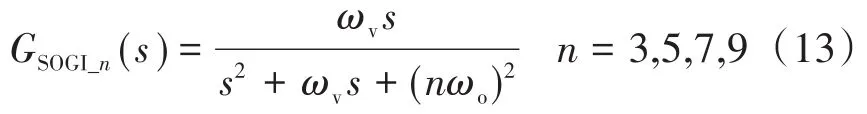
式中:ωv为带宽系数;ωo为基波角频率;n为谐波次数,为了实现电网中低频谐波的抑制,本文中n取3,5,7,9。
二阶滤波器GSOGI_n(s)的波德图如图9所示,该环节只对角频率为nωo的信号表现为通路特性,而对其余频段的信号表现为高阻特性,并且带宽系数ωv越大,滤波器的带宽越窄,信号提取的能力越强,故本文中ωv取30π。
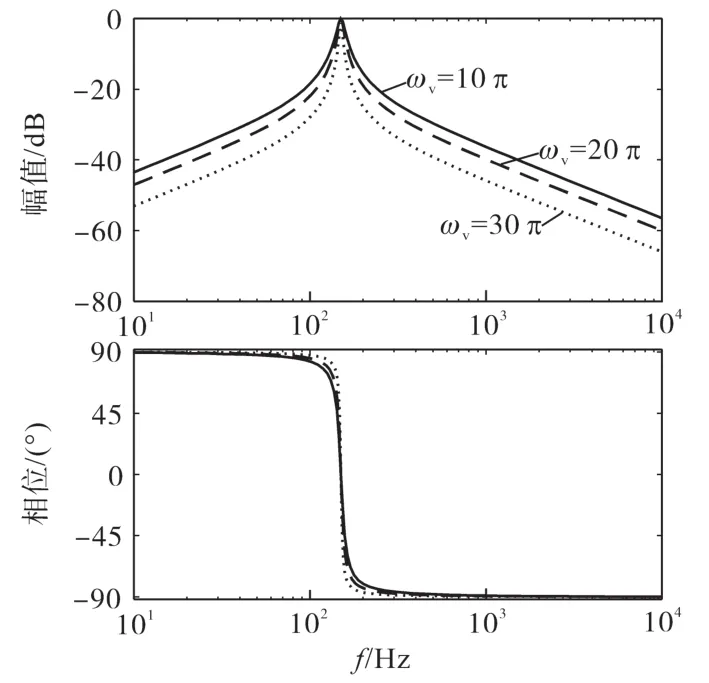
图9 二阶滤波器GSOGI_n(s)的波德图Fig.9 Bode diagram of second-order filter GSOGI_n(s)
为了描述所有的二阶滤波器对前馈通路幅频特性的影响,令所有滤波器并联构成的传递函数为Gt(s),其波德图如图10所示,表达式如下:
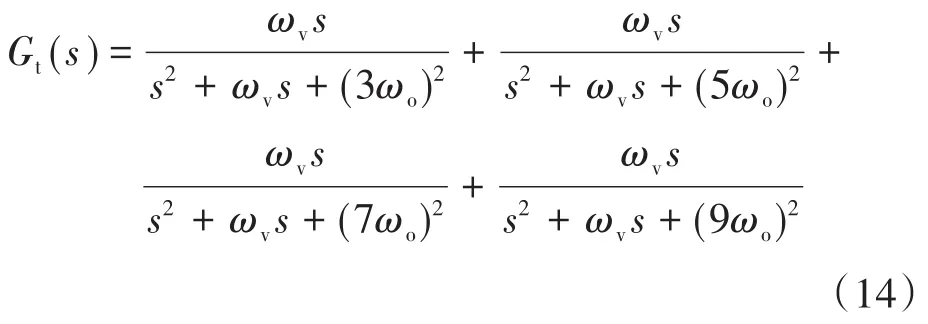
由图10不难发现,各特定次谐波信号的提取是互不影响,并联式的多二阶滤波器可以很好地提取各自的谐波信号,因此,我们可认为每个二阶滤波器之间是解耦的,所以在设计滤波器参数时,只需整定谐波信号的频率即可。
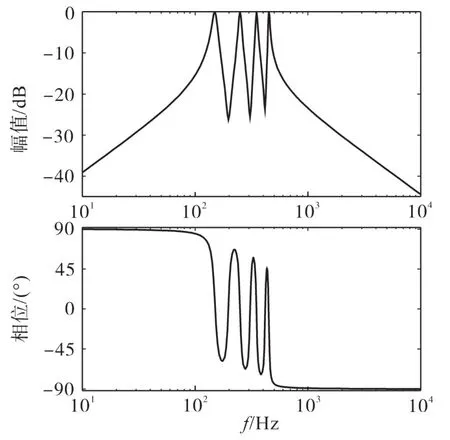
图10 并联式多二阶滤波器Gt(s)的波德图Fig.10 Bode diagram of parallel multiple second-order filter Gt(s)
3.3 改进后系统谐波抗扰能力分析
采用与第2节相同的分析方法,网压滤波前馈策略的电网电压扰动函数可列写为
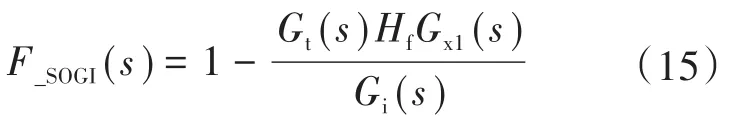
图11为F_SOGI(s)的波德图。
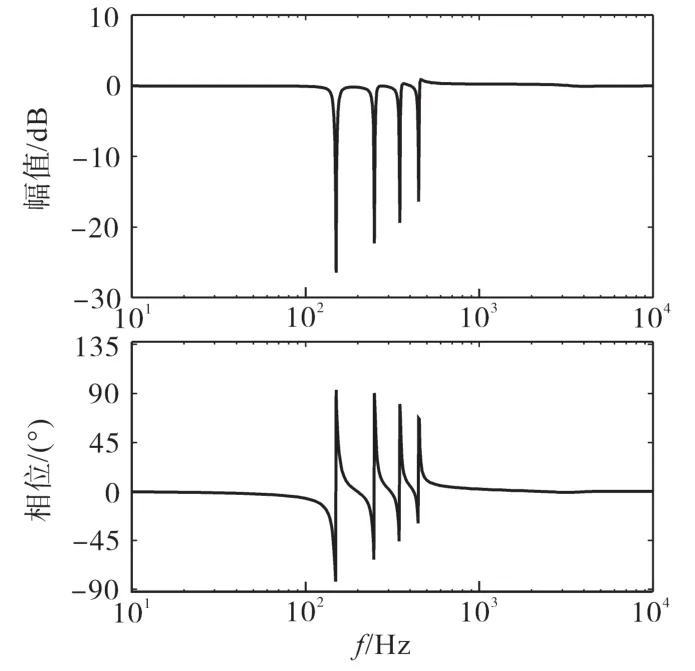
图11 电网电压扰动函数F_SOGI(s)的波德图Fig.11 Bode diagram of grid-voltage disturbance function F_SOGI(s)
从图11中可以发现,F_SOGI(s)在电网低次谐波频率处有很低的幅值增益,说明在这些频率处,F_SOGI(s)引入的upcc点等效干扰量基本趋近于0,表明并网逆变器可以很好地抑制这些低次谐波的干扰。但是同样的,由于延时环节Gkd(s)的存在,导致该策略的谐波抑制效果随着频率的增加而削弱,但upcc点的等效干扰量仍被抑制在-15dB以下,所以延时环节对该策略的谐波抑制效果影响可忽略不计。
3.4 改进后系统应对电网阻抗变化的稳定性分析
网压滤波前馈策略的输出阻抗Zo_SOGI(s)的表达式如下式所示:
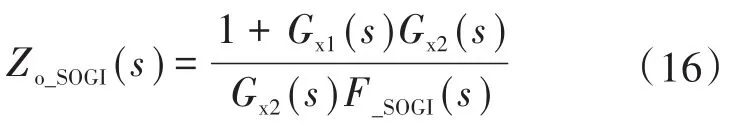
图12为Zo_SOGI(s)的波德图。从图12中可看出,相比网压比例前馈策略,该策略的输出阻抗Zo_SOGI(s)在中频段的相位远大于-90°,在电网阻抗Lg宽范围变化时始终拥有令人满意的相位裕度PM,表明了该策略在弱电网下具有良好的阻抗稳定性,而且从图12还可看出,该策略大大提升了并网逆变器在低次谐波频率处的阻抗幅值。
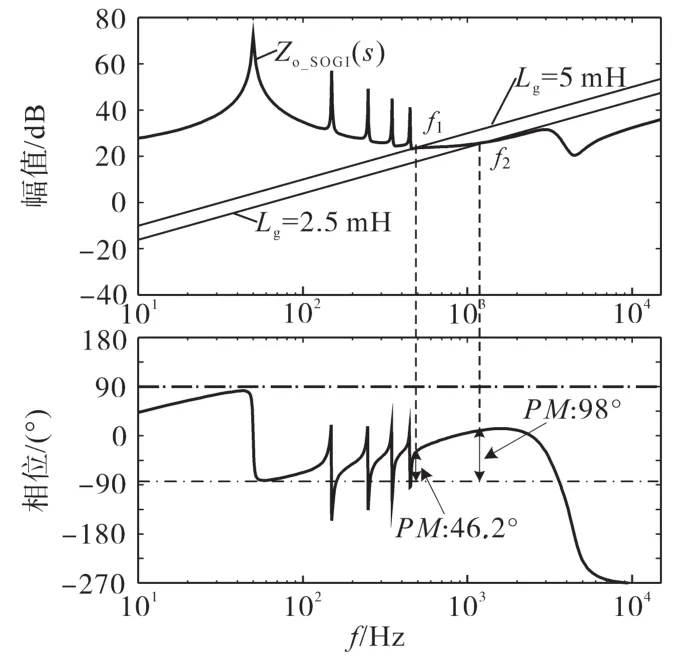
图12 输出阻抗Zo_SOGI(s)的波德图Fig.12 Bode diagram of output impedance Zo_SOGI(s)
综上所述,该策略既改善了并网逆变器应对电网阻抗宽范围变化的稳定性,又能提高对背谐波的抗扰能力,从而显著加强了并网逆变器对弱电网的适应性
4 仿真验证
为了验证本文提出的网压滤波前馈策略的有效性与正确性,通过仿真软件搭建了输出功率为4.5 kW的单相LCL型并网逆变器模型,并且对本文提出的策略与现有文章提出的自适应补偿策略,以及网压比例前馈策略进行了详细对比,仿真参数如表1所示。同时,为了模拟拥有丰富背景谐波和电网阻抗宽范围变化的弱电网,在仿真模型的电网电压中,加入了各次谐波与电感,各次谐波的含量用电网电压幅值的百分比来描述,如表2所示,三个策略入网电流的总谐波失真(total hormonic distortion,THD)在25个公频周期内进行快速傅里叶变换分析。
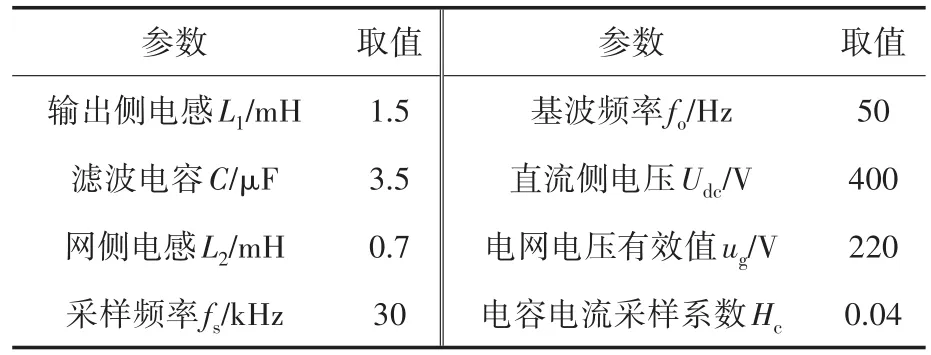
表1 单相LCL型并网逆变器的仿真参数Tab.1 Simulation parameters of single-phase LCL grid-connected inverter
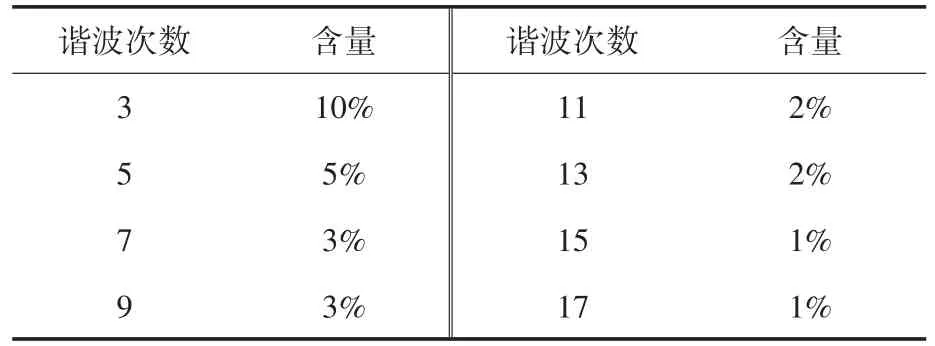
表2 仿真模型中弱电网的各次背景谐波含量Tab.2 Background harmonic content of weak grid in the simulation model
图13为Lg=0 mH时三个策略的入网电流ig和公共耦合点电压upcc的仿真波形。从图13a中可看出,网压比例前馈策略在强电网条件下有很好的谐波抗扰能力,各次谐波分量都能得到有效抑制,使得并网逆变器的入网电流质量较高;在图13b中,本文提出策略的入网电流的THD同样保持良好,验证了本文提出策略对电网低频背景谐波同样具有较好的抗扰能力;而在图13c中,自适应补偿策略需要间歇性注入一定的高频谐波电流用于检测电网阻抗,导致入网电流质量被恶化,但是谐波注入周期仅为2个周期,所以对系统的影响不大。
图14为Lg=2.5 mH时三个策略的入网电流ig和公共耦合点电压upcc的仿真波形。由图14可看出,网压比例前馈策略受到电网阻抗变化的影响,背景谐波被一定程度地放大,入网电流的THD增加,而本文提出策略对电网阻抗变化的敏感度较低,基本不受影响,另外,自适应补偿策略的实现效果同样较为理想,与本文提出策略的入网电流THD基本一致。
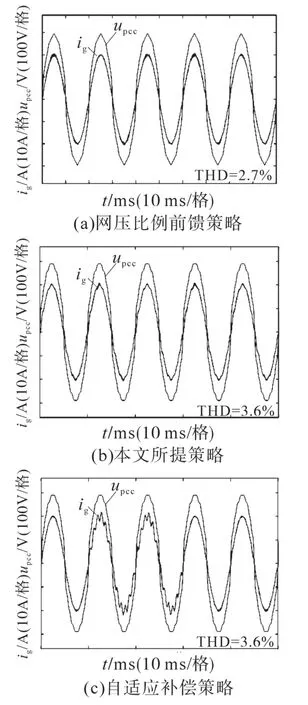
图13 Lg=0 mH时三个策略的仿真波形对比Fig.13 Simulation waveforms comparison of three strategies when Lg=0 mH
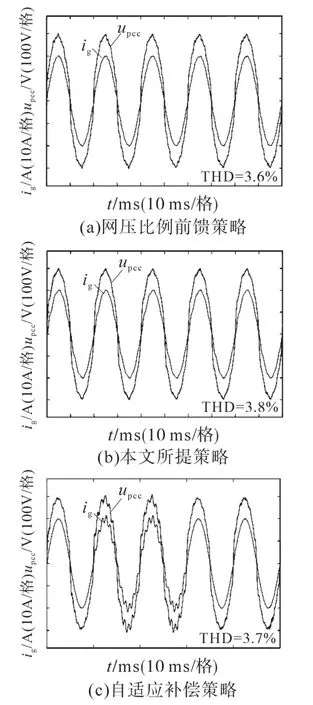
图14 Lg=2.5 mH时三个策略的仿真波形对比Fig.14 Simulation waveforms comparison of three strategies when Lg=2.5 mH
图15为Lg=5 mH时三个策略的入网电流ig和公共耦合点电压upcc的仿真波形。不难发现,网压比例前馈策略中的背景谐波被大幅放大,入网电流质量糟糕,无法满足分布式发电系统的并网标准,验证了第2节分析的正确性,而本文提出策略兼顾良好的谐波抗扰能力与稳定性,电网阻抗Lg在0~5 mH内变化内,并网逆变器均能输出质量良好的入网电流,相比于自适应补偿策略,本文提出策略的最终实现效果与其几乎相近,但是自适应补偿策略需要复杂的电网阻抗测量技术,严重加大了系统的计算量,而本文提出策略的计算复杂度远小于自适应补偿策略,实现方式简单有效,并且,新引入的二阶滤波器也不含微分项。
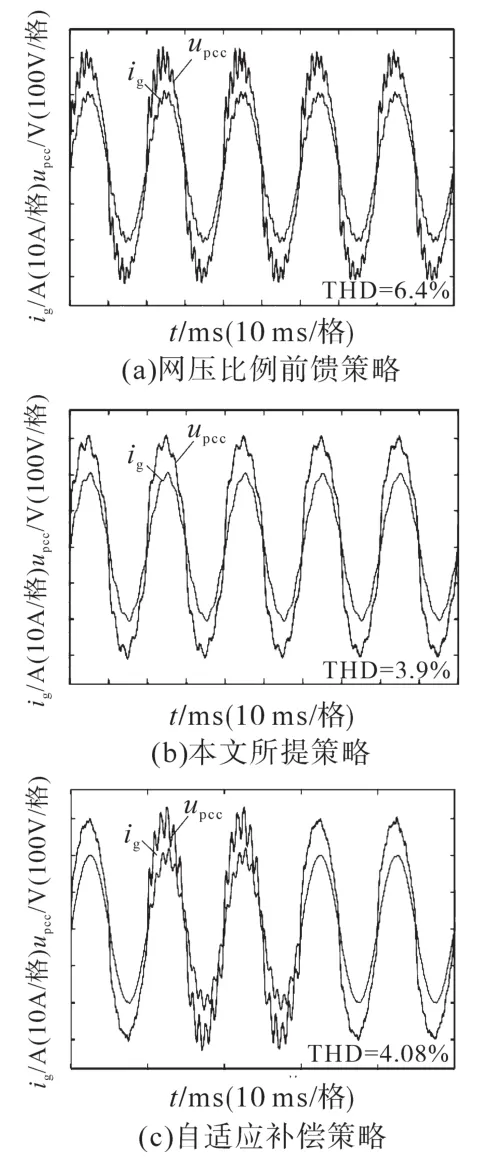
图15 Lg=5 mH时三个策略的仿真波形对比Fig.15 Simulation waveforms comparison of three strategies when Lg=5 mH
5 结论
本文首先详细推导了并网逆变器在弱电网下的输出阻抗模型,输出阻抗能反映并网逆变器对谐波的抗扰能力和对电网阻抗变化的稳定性,当前广泛使用的网压比例前馈策略在弱电网下的适应性糟糕,不宜采用。为此,本文提出一种网压滤波前馈策略,该策略可使系统在弱电网下同时兼顾良好的谐波抗扰能力与稳定性,显著提升了并网逆变器在弱电网下的适应性,并且与已有文献提出的自适应补偿策略相比,本文提出策略的实现效果与其接近,但是系统计算复杂度远小于自适应补偿策略,且不含微分项,无放大高频谐波的副作用。接下来将针对二阶滤波器的算法复杂度作进一步简化,并将该策略应用于三相并网逆变器。

