生态河道中多尺度水力学及水动力学问题浅谈
潘文浩,尚 钦,汪洹湛
(长江勘测规划设计研究有限责任公司,湖北 武汉,430010)
0 引言
在生态文明建设的大背景下,河道的生态环境治理问题显得日益迫切和必要。根据生态环境部对于相关中小河流河道生态修复的技术指南要求,河道的生态治理的基本需求为在保证河道防洪、航运、灌溉等基本功能的前提下,充分考虑生态环境、水质净化、亲水景观等需要,使河道资源可持续利用和生态环境健康紧密结合[1]。以往在河道生态修复研究中,从事生态环境及动植物研究的学者习惯于从河道生物群落结构、水质净化、水生生物的生存习性等方面来进行研究,而长期从事水动力学和河道研究的学者则往往是出于防洪、航运、灌溉等方面的需求来进行研究,两者缺乏对河势控制、水流条件与河道生态功能定位之间的有机结合。事实上,水动力学过去几十年的发展已有相当可观的成果,而生态河道中的一系列生态问题如生物物理过程、污染物输移、营养物输运等均与不同尺度的水力学及水动力学问题有着密切联系。比如从微观上讲,泥沙颗粒能为微生物提供生存环境;合适密度的水生植被通过改变河道流速分布和泥沙输运,能提供空间上非均匀的栖息地条件,从而促进生物群落的多样性;卵石河床在河道表层水流动量输运与潜流带渗流过程的综合作用下,能为底栖生物提供良好的生存环境[2];从流域及更大的时间尺度上讲,大洪水引起的河道形态调整往往能极大地摧毁并重建整个河道的生态系统。因此,在河道的生态治理中应充分结合水力学及水动力学与生态问题。本文拟对生态河道中涉及的不同尺度的水力学及水动力学问题进行定义和分类,并初步探讨各尺度水力学及水动力学问题的基本理论方法以及它们之间的结合。
1 单棵植被尺度
1.1 单棵植被尺度的基本理论
在单棵植被尺度时,水流流经植物表面,其水动力学过程符合最基本的边界层流动特性,该过程对植被附近的质量(如溶质、气体等)扩散起到重要作用,其基本水动力学模型可见图1(图中,x表示距离,u表示流速,下标1、2、3分别表示纵向、横向、垂向,下同)。植被与水流的边界形成一个粘性边界层,其厚度δ随着水流方向增加并符合如下分布特性(其中U为水深平均流速,ν为运动粘度,x1为沿水流方向距离)。在一定的扰动条件下,发展成紊流边界层,转戾点一般发生在R=x1U/ν≈5×105处。紊流边界层在垂向上则可分为粘性底层、缓冲层和半对数层。粘性底层和半对数层的物理过程(包括动量、质量输运)有着数量级的区别,前者主要由壁面摩阻流速u*、分子运动粘度ν、分子扩散系数Dm决定,而后者则主要由离植物表面或床面的距离x3、粗糙度Δ来决定,这对于生物生长所需的氧、氮、磷等溶质输运起到重要作用。具体来说,在粘性底层,质量通量dm/A12dt符合菲克定律
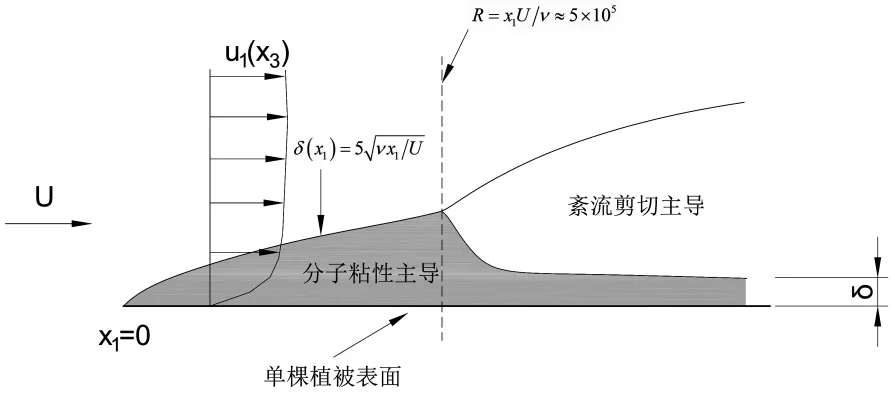
图1 植被表面紊流发展过程

式中,m为质量,A12为垂直于x3方向的单位面积,∂C/∂x3为沿垂向的浓度梯度,C为溶质浓度。由式(1)可知,在植物表面,营养物溶质的输运取决于两方面,一是植物本身对营养物溶质的吸收速率,另一个就是式(1)所示的物理扩散速率。若植物的吸收速率足够大,植物表面的溶质浓度趋于零,则粘性底层可以不断地形成较大的浓度梯度。关键在于找到植物本身吸收和物理输运供给两者的平衡。我们首先要把浓度梯度∂C/∂x3简化为更易测量的物理量,由于粘性底层足够薄,假设∂C/∂x3=C/δ,代入(1)则有

如此,质量通量便与自由流的平均速度有直接关系。从物理-生物过程来理解,随着流经植物表面的平均流速增加,粘性底层变薄,垂直于叶片表面的物质输运增加。所以对于流速缓滞区,在不考虑沉积等其他作用的前提下,植物所得到的养分会比较少,适当的流速对植物生长是有好处的,而流速过大,植物本身的吸收速率小于供给量。国内外已有学者对这个特征流速进行过研究。如文献[3]通过实验观测到对于海草的平衡流速为U=4~6cm/s。这说明在流速小于4~6cm/s的水流中,植物会因为养分供给不足而影响生长,因此,在河道与湖泊的生态绿化中,需保持河流、湖泊的水系连通性和一定的生态流速。
1.2 小结
在单颗植被尺度时,植被的生长条件与水流流速有着密切关系,在河道、湖泊的生态绿化中,应保证水系的连通性,避免形成死水,以保证植物的营养吸收,同时,应根据河道、湖泊水文特性选用合适植被品种,如在流速较小的湖泊,可选用枝叶较小的植被,在流速较大的河道,可选用根系发达、耐冲刷的品种,并结合混凝土网格块、格宾网箱等护坡固土结构栽种。
2 植被丛尺度
2.1 植被丛的水流运动方程


图2 河道生态系统中不同尺度的水动力学过程

图3 单位体积迎流面面积示意图
植被丛里的水流流态可以认为是圆柱绕流的叠加,因此,从单棵植被尺度来看,其流场是空间上非均匀的。为求解植被丛尺度的流场,我们则可以引入双平均法来消除流场局部的非均匀性。双平均法类似于雷诺平均法,包括时间和空间上的平均。采用角括号来表示双平均的流场统计量,双撇号表示因局域平均产生的空间脉动量,即对于场变量ψ,有

根据以上双平均方法,我们可得到双平均处理后的水流运动方程如下
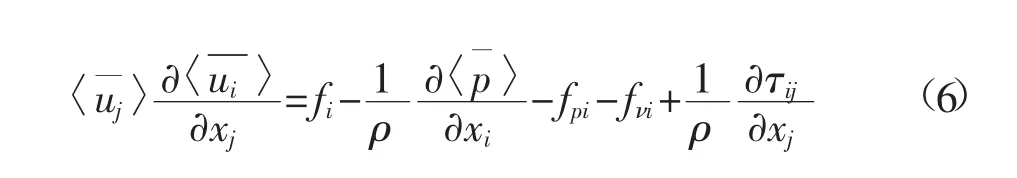
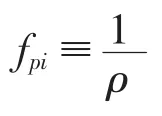
对水流流场的二阶统计量如紊动能、雷诺应力也进行相应的双平均,便可进一步构建流场的封闭模式。具体的推导可见文献[4]。
2.2 植被丛分布对水动力特性的影响
对于生态河道,在植被丛的尺度上,如图4所示,有几种不同尺度的紊动能产生项。第一种是茎秆尺度的紊动能。首先,定义Red≡Ud/ν为植被茎秆雷诺数,当Red足够大时,植被茎秆直径d远大于Kolmogorov微尺度η,受植被茎秆的阻水作用,会产生茎秆尺度(包括茎秆直径d、茎秆间距S)的紊动。若植被分布稀疏(d<S),则紊动能产生的尺度为d,反之则是S。根据相关实验证明,即使在植被分布非常稀疏的情况下,植被茎秆产生的紊动能也要强于河道床面剪切作用产生的紊动能,也就是说,在植被丛中,床面摩阻流速u*基本可以忽略,水流的平均动能全部由茎秆阻水作用转化为茎秆紊动能,并进一步通过能级耗散。据此,茎秆紊动能的平衡方程可简化为
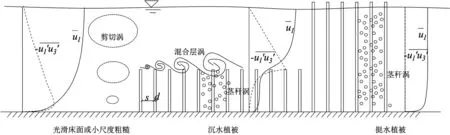
图4 植被丛的不同尺度紊动能产生项

式中,k为紊动能,CDp为植被拖曳力系数,u1为纵向流速。上式可直接应用于挺水植被流或沉水植被流中植被层部分。其物理意义与我们对植被丛中水动力学特性的直观认识是相符的:紊动能在植被丛沿垂向的分布基本是均匀的,紊动能的产生和耗散达到平衡,且雷诺应力趋于零,沿垂向的动量交换非常微弱。也就是说,在植被分布密度足够大时,水体中的溶质输运在植被丛内仍然是以分子扩散作用为主,垂向的剪切弥散起到的作用相对较小。
第二种是明渠床面剪切紊动能,其尺度与离床面距离相关,它与光滑床面的明渠中的剪切紊动能没有太大区别,所不同的只是其产生是由植被扰动形成,且由植被顶部而不是床面发展至自由面。第三种则是植被层顶部形成的Kelvin-Helmholts涡结构[5],一般称为混合层紊动能,其产生机制可理解为平均动能和剪切紊动能为克服植被阻力作用而形成的涡结构,它的平衡过程为:不断从平均动能和剪切紊动能吸取能量,并转化为更小尺度的茎秆紊动能,因此其尺度介于第一种和第二种紊动能之间,相关实验也证实了它与植被的拖曳长度尺度(CD)a-1相关[6]。这个尺度的紊动能对植被顶部的动量输运起到了非常关键的作用,根据Nepf等[7]的实验观测,它向植被层以内渗入的深度为
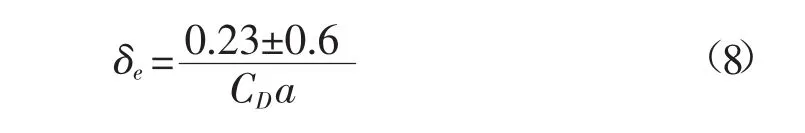
式中,CD为拖曳系数。上式对于生态河道中的植被床面和卵石床面均有一定的指导意义。植被顶部以下一定深度内的动量交换与表层水流仍然十分密切,这就决定了水体中的溶质交换主要以水动力剪切弥散作用进行。相关实验和原观资料也验证了这一点,比如针对山区河床生态群落的研究表明,相对于潜流带,水生生物在顶部河床处分布密度最大,多样性最广。
综合以上分析可知,植被丛的分布密度对水动力特性有着极大影响,进而也影响相应的溶质输运。
3 河道尺度
在河道尺度上,水流边界条件更为错综复杂,如河道形态是蜿蜒曲折的,河道的缓冲带、岸坡带、基底带的动植物和微生物分布各不相同,这就需要对前两节中的相关尺度描述进行升级。在河道尺度上,我们要讨论河道总体阻力、过流流量、水质净化能力、合适的植被分布等问题时,再对整个河道的水动力学特征量求解到植被丛尺度已是不现实的,这就需要对相应的物理量进行概化描述。具体来说,需要对植被丛尺度内的水动力特征量进行一定体积上的积分,并建立其与更易于测量的植被特性之间的关系。
3.1 植被丛的积分描述
对于植被丛,沿水流方向的运动方程(6)可简化为

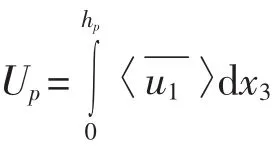

式中,hp为植被高度;H为水深;τh为植被层和水流层交界面(x3=hp)的切应力。根据沿湿周平均的切应力与能量损失系数及平均流速的关系,有
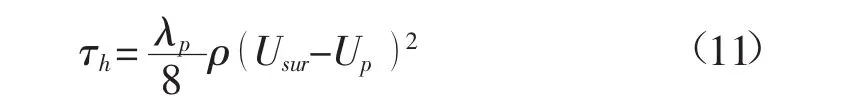
式中,λp为由于植被层阻力造成的表层流动的能量损失系数。要求得植被层和表层的水深平均流速,需要确定λp的先验值。
根据文献[4]对大量实验数据的统计分析,λp与植被分布的密度、相对水深等特性的相关性相对较弱,其取值区间位于 λp≈0.02~0.5,且在 λp≈0.16 时,各种工况条件下的数据均方差最小。这里采用该值来计算水深平均流速。将式(11)代入式(10)便可得到
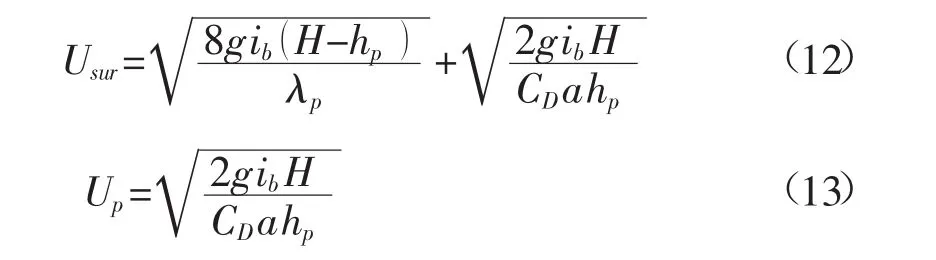
沿水深平均的流速则为
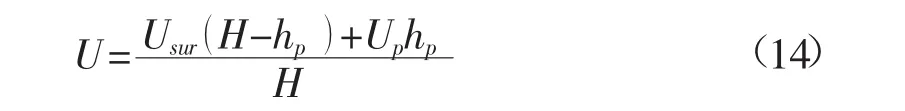
对于圆柱形刚性植被,取CD=1.7时,计算值与不同实验值比较如图5所示。图中给出了原观数据以及相应实验数据[4]。由图可知,计算值与不同的实验数据均基本吻合。
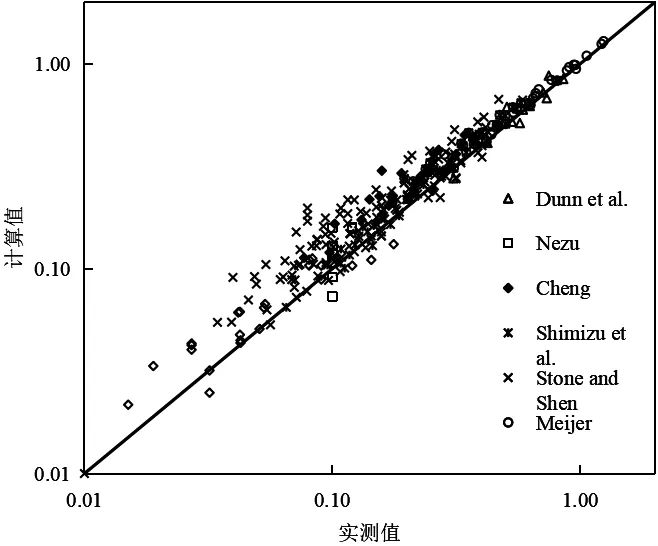
图5 计算水深平均流速与实测值的比较
3.2 河道尺度的植被阻力
植被片区由不同的植被丛部分组成。定义植被阻水率△Sp为植被片区占河道过水面积的比例,如图6(a)所示。图中,Uw为水流区的流速,Up为植被区流速,Bpi为植被片宽度。对植被片区宽度进行一定的区域平均,得到横断面上的植被片宽度为

概化后的横断面图如图6(b)所示,图中,B为明渠底宽,Lb为植被片间距之和。沿水流方向单位长度的横断面上植被区与水流的交界面面积Lp为
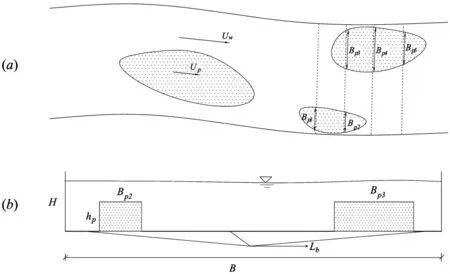
图6 河道尺度的植被特性概化图

其中N为横断面上植被片区的数量。
则植被区的阻水率,△Sp为

当植被布满河床时,Bp≈B,阻水率即为相对淹没度△Sp=hp/H。
对运动方程在沿流向单位长度的控制体上积分,得到:
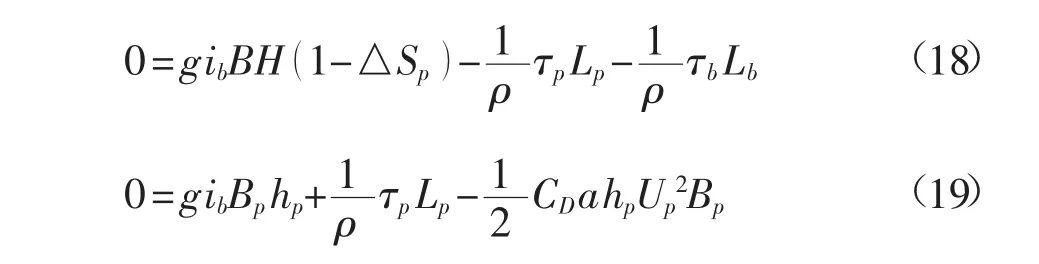
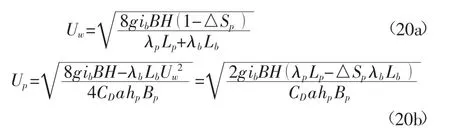
断面平均流速为
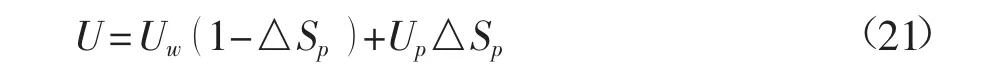

采用上式来计算天然河道的糙率系数时,时均流速计算式中的系数较多,根据天然河道的一些特征,可对其进行相应的简化。
当明渠足够宽浅且植被片在河道中的分布较稀疏时,可认为Lp+Lb≈B,进一步采用统一的能量损失系数λ0代替λp和λb,再比较植被区和水流区的时均流速计算式(20a)与(20b),由于△Sp较小,且在植被茎秆分布较密的情况下,因此植被区的流速在量级上要小于水流区的流速,在式(22)中忽略掉植被区流速,得到
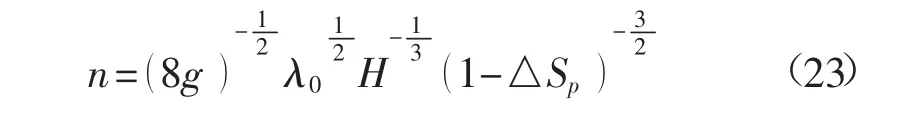
经过上述简化,糙率系数变为植被的阻水率的函数,仅需率定λ0的取值。采用文献[8,9]的原观资料来与上式计算成果进行比较,如图7所示。
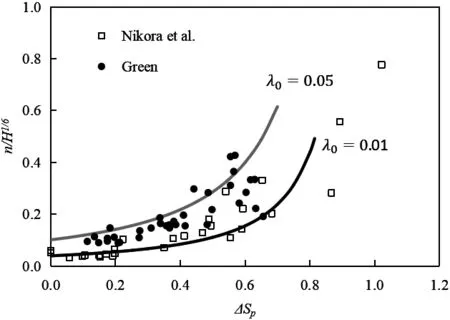
图7 天然河道糙率系数与植被群阻水率的关系
图中采用H1/3来对糙率系数无量纲化,当λ0的取值在0.01~0.05之间时,采用式(23)计算所得的糙率系数能基本包络相应的实测值,特别是在阻水率较小时;在阻水率大于0.8之后,式(23)与实测成果有一定偏差,此时忽略植被区的流速的假设不成立,仍需要采用式(22)来进行计算。
4 总结与展望
4.1 总结
本文对生态河道中不同尺度的水动力学问题作了基本的概述和初步探讨,主要结论总结如下:
(1)在单颗植被尺度时,水流中植被表面的溶质输运包括分子粘性扩散和紊流弥散两种尺度,将其简化后可采用水流平均流速来描述。当水流的流速达到4~6cm/s时,对于海草等水生植被,水流的溶质供应与植被表面对溶质的吸收速率达到平衡。因此,河流、湖泊的水系连通与一定的生态流速对于植被生长有着重要作用。
(2)在植被从尺度时,宜采用双平均法来建立植被水流的水动力学模型,植被特性可采用单位体积迎流面面积以及拖曳系数来描述,并据此建立流速分布与植被特性的关系。理论模型及相关实验表明,水流的剪切弥散作用对植被丛中的溶质输运具有重要作用,合理的植被高度、分布密度能保证植被层的养分供应。
(3)在河道尺度,对于足够宽浅且植被区阻水率不大的情况下,河道的糙率系数可进一步简化为植被阻水率的函数,根据简化后的计算式所得的计算成果与天然河道的原观成果吻合较好。因此,在计算生态河道的水力学特征量时,可测量植被丛的阻水率,并根据本文率定的相关参数来进行计算。
4.2 展望
本文仅对生态河道中的水力学及水动力学问题作了初步探讨,以求抛砖引玉,引起更多从事水力学和水动力学方面研究的学者从河道生态角度来考虑一些基本问题。本文的初步探讨也表明,植被的生物-物理特性、植被丛分布等均与水流之间有着非常强的相互作用,在河道治理中应选择合理的治理方式来兼顾河道的生态治理与水利需求。
在不同尺度描述以及之间的结合仍然大量地依赖于简单概化的水槽试验成果,生态河道中的原型观测成果以及一些流体力学与水动力学方面相关的理论基础还待进一步补充完善,对于生态河道中更为复杂的柔性植被、浮游生物、植物-泥沙交界面等边界条件下的水动力学问题仍然需要更进一步的研究。

