求解变分不等式问题的惯性次梯度外梯度算法

米特特， 方长杰

（重庆邮电大学 理学院，重庆400065）

考虑如下变分不等式问题（VIP），即寻找点x*∈C使得

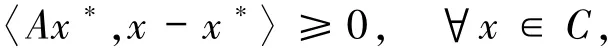
其中，A：H→H是一个连续映射，H为Hilbert空间，C⊂H是H中的非空闭凸集，〈·，·〉和‖·‖分别表示H中的内积和范数.记Ω为变分不等式问题（VIP）的解集，即点x*∈Ω满足上式.用PC（x）表示点x到非空闭凸集C上的投影，即PC（x）＝argy∈mCi n ‖x-y‖.

变分不等式理论已广泛应用于障碍问题、力学中的单边问题、平衡问题等，参见文献［1-3］及其参考文献.为了探索和分析相关的收敛结果与误差界，求解变分不等式问题（VIP）算法的研究引起了许多学者的关注.例如外梯度算法［4］、次梯度外梯度算法［5-6］.另外，惯性算法在近些年也引起了大家的兴趣，参见文献［7-8］.

最近，Thong等［8］提出了求解变分不等式问题（VIP）的如下算法：

在映射A是单调且Lipschitz连续的假定下，证明了上述算法所产生的迭代序列｛xn｝强收敛到点p∈Ω，其中p＝PΩ◦f（p）.

另外，Migórski等［9］提出了求解变分不等式问题（VIP）一种新的次梯度外梯度算法：

其中在映射A是单调且Lipschitz连续的假定下（Lipschitz常数不需要知道），他们证明了算法迭代所产生的序列｛xn｝强收敛到点p∈VI（C，A），其中p＝PVI（C，A）◦f（p）.

Bot等［10］提出了Hilbert空间中求解变分不等式问题（VIP）的如下Tseng向前向后算法：

在映射为伪单调，Lipschitz连续且序列弱-弱连续的假定下，他们证明了由上述算法所产生的迭代序列｛xn｝弱收敛到点p∈Ω.

从以上工作中得到启发，本文提出了求解变分不等式问题的一种惯性次梯度外梯度算法，并且在映射A是伪单调，Lipschitz连续的（Lipschitz常数不需要知道）且序列弱-弱连续的假定下，证明了算法所产生的迭代序列｛xn｝强收敛到点p∈Ω，其中p＝PΩ◦f（p）.最后通过数值实验将所提的算法与文献［9］中的算法1和文献［8］中的算法3.1进行了比较.与此同时，在文献［8-9］中，映射A假定是单调的，而在我们的算法中，映射A只需要是伪单调的.相比较文献［10］中的弱收敛性，得到了强收敛性的结果.

1 预备知识

本节将介绍一些将在下文中使用的引理.首先，有如下定义.

1）xn→x表示序列｛xn｝弱收敛到x；

2）xn→x表示序列｛xn｝强收敛到x.

定义1.1 设A：H→H为映射算子，则：（i）称A是单调的，如果

（ii）称A是伪单调的，如果对于∀x，y∈H，都有

（iii）称映射A是Lipschitz连续的，如果存在常数L＞0满足下式

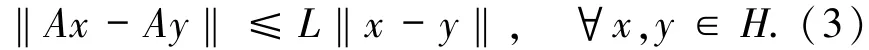
（iv）称算子A是序列弱-弱连续的，如果对任意的序列｛xn｝弱收敛到x，则序列｛Axn｝弱收敛到Ax.

注1.1 在定义1.1（iii）中，如果L∈［0，1），则映射A称为压缩映射.

引理1.1［11］设H为实Hilbert空间，则有：

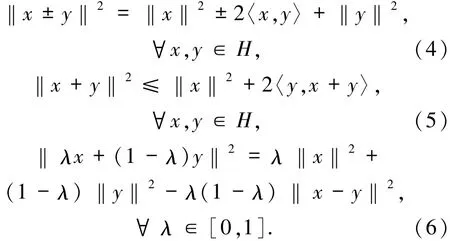
在证明以下算法2.1的收敛性时，以下2个引理起着十分重要的作用.

引理1.2［12］设｛an｝和｛αn｝为非负实序列且αn∈（0，1），∑∞n＝0αn＝ ∞.如果存在序列｛bn｝，limn→s∞u pbn≤0，当N＞0时使得an+1≤（1-αn）an+αnbn，∀n≥N成立，则有liman＝0.

2 主要结果

3 数值实验

本节将对所提出的算法进行了一些对比数值实验.MATLAB代码运行在PC（AMD酷睿（TM）A8-4500M APU＠1.90 GHz）下，在Matlab版本8.4.0.150421（R2014b）Service Pack 1上运行.当‖xn-x*‖≤ε时，迭代停止.用“ISEA”“iTEM”“MSEM”分别表示本文中算法2.1、文献［8］中算法2.1和文献［9］中算法1.

例3.1 设H＝Rn，n＝10且

定义映射A：Rn→Rn为A（x）＝Mx+d.M由下式随机生成：

其中，N是n×n阶矩阵，B是n×n阶斜对称矩阵，且矩阵N和B中的元素都属于（-2，2）.矩阵D是n×n阶对角矩阵，且对角线元素取值范围为［0，2］.所以易证矩阵M是正定矩阵.方便起见，选取向量d为零向量.

例3.1能在文献［18］中发现，其中算子A为单调的.由于矩阵M是正定矩阵，所以A是L-Lipschitz连续的且L＝‖M‖.取f（x）：＝x/2.迭代初始点为x0＝x1＝（1，0，…，0）∈Rn，容易证明x*＝0是变分不等式问题（VIP）的解.进一步，选取λ0＝τ＝0.9，μ＝0.5以及

针对文献［8］中算法2.1，取λ＝0.8，αn、βn和上述相同.针对文献［9］中算法1，选取αn＝0.53，γ＝0.4，λ0＝0.7.数值对比结果图参见图1.

图1 例3.1中‖x n-x*‖随时间变化曲线图Fig.1 Time curve corresponding to‖x n-x*‖in Example 3.1

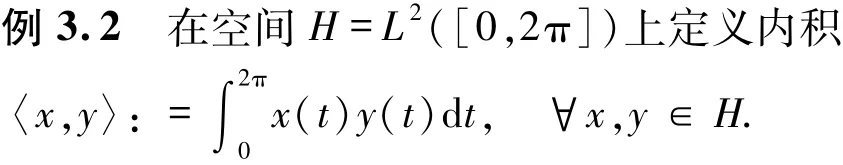
定义范数为

图2 例3.2中‖x n-x*‖随时间变化曲线图Fig.2 Time curve corresponding to‖x n-x*‖in Example 3.2