观点动力学研究现状及进展述评
刘举胜, 何建佳,韩景倜,于长锐
(1.上海财经大学信息管理与工程学院,上海 200433;2.上海理工大学管理学院,上海 200093;3.上海金融智能工程技术研究中心,上海 200433)
0 引言
观点作为个体的一种思维、意见和态度的表现形式,广泛存在于公众生活之中。近年来,随着Web2.0的迅速崛起,利用互联网平台在网络社区中进行发声与评议逐渐成为公众的日常活动。在网络社区中,公众利用微信,微博,QQ等互联网平台表达自我观点,发表个体看法。多个观点的出现以及个体间观点的不断交互,使得群体观点逐步呈现出一致、分散和极化等不同现象。不同的观点演变结果在传播信息的同时也为网络舆情治理带来了各种挑战,如消极观点的蔓延和恐慌观点的传播就会给舆情的治理带来一定困难。因此如何对不同观点的演化进行深入研究,对理清观点演变机制,实现舆情的合理管控,构建媒体融合发展态势具有重要的理论与现实意义。
演变作为一种动态变化过程广泛存在于自然界与人类发展史中,一致、分裂与极化是演变过程中存在的三种现象。观点作为个体主观意愿的表现形式,也具有上述特征。学术界最早对观点的演化研究起始于Degroot[1]在《Journal of the American Statistical Association》发表的“Reaching a Consensus”一文,在该文中Degroot探讨并解析了群体观点的共识过程,指出观点是服从于含参的某种概率分布。在此基础上,研究者们结合社会学、心理学、组织行为学等多种学科知识,对观点演化模型进行了大量研究,形成了不同的观点演化模型。其中根据观点的表现形式将观点分为离散形式和连续形式;根据个体的数量将观点演化模型又分为二元观点演化模型和群体观点演化模型。
目前,已有文献[2-3]对观点动力学现有研究进展进行了相关综述,然而,研究多集中于展现国外研究成果,对国内观点动力学研究进展介绍较少,虽然任立肖等[4]也对国内观点动力学研究现状进行了梳理,然而该文献对二元观点演化动力学介绍较少,难以呈现二元观点演变研究范式以及二元观点与群体观点之间的联系。基于此,本文通过对国内外二元观点动力学及群体观点动力学的基本模型及现有研究进展进行梳理,以期为未来观点动力学研究提供一定启示与参考。
1 国内外观点动力学研究现状
从国内外现有观点动力学研究来看,根据个体的数量,观点演化可以分为二元观点演化和群体观点演化,此处,“元”代表个体数量。其中,在二元观点演化研究方面,现有研究在充分考虑个体交互过程中呈现的“经济人”特征和“有限理性”特征基础上,大多借鉴博弈论思维进行研究。其中,Mare[5]和Ding[6]较早对二元观点演化动力学进行了探究,作者将观点的演化过程类比为两个体博弈过程,并假定参与方的博弈策略选择分别为改变,保持和同意三种策略,通过求解不同条件下系统的均衡状态,最后得出了若干有价值的结论。该研究为二元观点演化提供了一定研究范式,后续研究在此基础上进行了大量改进,为探究二元观点演化提供了很好的研究基础。在群体观点动力学方面,研究者根据观点的离散和连续表现形式,综合个体交互形式,提出了一系列群体观点演化模型。其中较为经典的离散观点动力学模型有:Ising模型[7];Sznajd模型[8];投票模型(Voter model)[9];大多数模型(Majority Vote model)[10]。连续观点动力学模型主要包括DW模型[11]和HK模型[12]。观点动力学研究框架如图1所示。

图1 观点动力学研究框架
2 二元观点动力学模型及研究现状
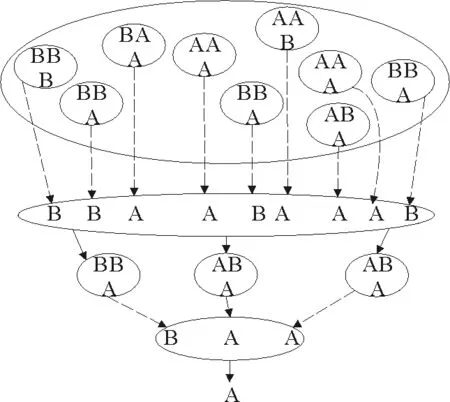
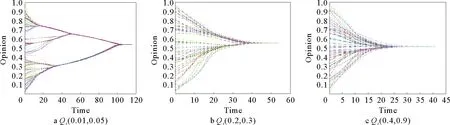
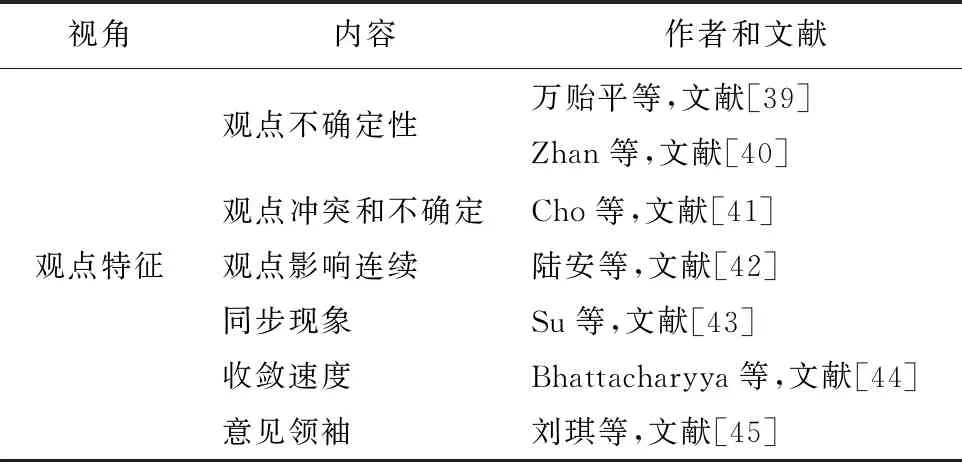
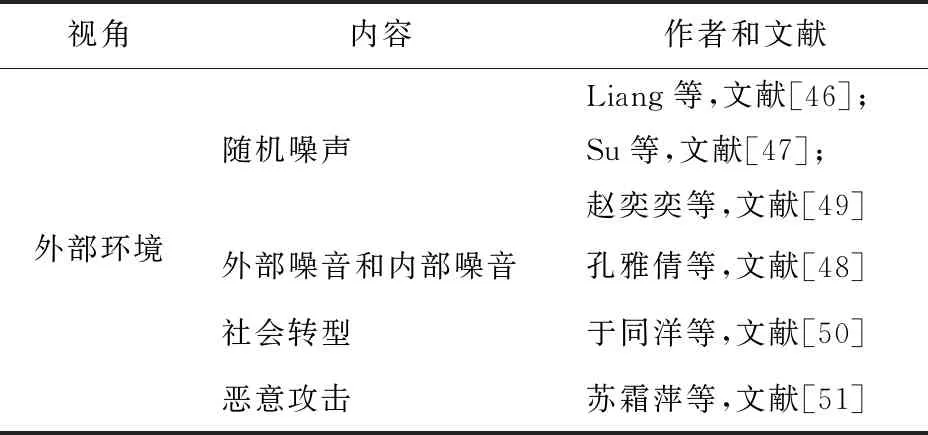
博弈论作为一种策略选择和演化理论,在二元观点动力学建模过程中,发挥了重要的作用。国外方面,现有研究大多借鉴Mare等[5]和Ding等[6]的研究思想,将改变观点、保持观点、妥协到中间值,以及退出交互等策略作为博弈方的策略空间,对二元观点的演化进行探究。其中,Mare等较早对二元观点动力学演化进行了建模,提出一种包含改变观点、保持观点、妥协到中间值的观点博弈模型。在该模型中,作者分别利用Si(t)和Sj(t)表示参与者i和j的观点,利用d=Sj(t)-Si(t)表示观点的距离。并且定义各策略收益:令j的观点完全改变时,i获取的收益为a;j的观点没有改变时,i损失的收益为b;j的观点改变一半,即达到中间值时,i获得的收益为c;其中0 在该模型中,当d≤1/(b+c),支付矩阵的纳什均衡策略为(3,3),这意味着两个参与者观点将达到一致;当d≥1/(b+c),支付矩阵的纳什均衡策略为(2,2),这意味着两参与者都选择保持策略。此时,该博弈模型可以简化为一个固定参数a,b,c,阈值ε=1/(b+c),u=0.5的一个DW观点动力学模型,具体表达形式为:Si(t+1)=Si(t)+μ[Sj(t)-Si(t)],Sj(t+1)=Sj(t)+μ[Sj(t)-Si(t)],这种转化体现了二元观点动力学与群体观点动力学之间的内在联系。Mare主要对博弈双方交互过程中观点的演化过程进行模型化,该模型能够较好地展现参与方观点演化特征,对后续在二元观点建模方面的研究提供一定参考。 随后Ding在Mare的基础上,进一步考虑了交流成本和交流可退出的情形,设计了保持观点、改变观点到中间值,交互退出三策略的博弈模型,具体博弈支付矩阵如表2所示。在该模型中,e表示参与讨论所浪费的时间和精力,此处,e 表1 i的博弈支付矩阵[5] 表2 i的博弈支付矩阵[6] 基于上述研究,后续研究大多通过对博弈双方收益函数的精确刻画并利用参与方观点相互博弈的思维范式对二元观点动力学展开探究,如Abtoy[13]利用Petri网刻画收益函数,提出了一种基于在线视频社交网络(OVSN)的在线用户个体意见模型;Chen[14]等通过引入社会偏好理论将互联网用户分为利己、利他和公平偏好三种群体,并采用收益函数对不同偏好个体在互动过程中所获得的收益进行定义,分析了不同偏好以及个人收入对舆论两级分化效应的影响;Bu等[15]将情感计算与观点演化进行结合,利用博弈理论以天涯论坛的评论对情感的进化进行了预测研究。在该研究中,作者认为若一方对另一方的评论是积极的,另一方就会感到高兴,其效用就会增加,反之其效用就会衰减,研究从评论交互视角出发,对二元观点演化机制进行了新的拓展。 国内方面,学者们从个体交互特征出发对二元观点动力学进行了进一步拓展,如引入话题引力和阻力概念,决策主体的记忆和学习机制等,并将二元观点动力学应用于舆情治理和行为决策中。熊菲等[16]根据个体观点的更新过程,将改变观点和保持观点作为博弈方的策略空间,建立了不完全信息下连续观点演化博弈模型;宋彪等[17]将话题阻力和引力概念引入观点演化过程中,构建了信任与不信任某一话题观点博弈策略空间,对网络舆情的疏导进行了相关研究;雷丽彩等[18]在考虑决策者不同个性特征的基础上,通过引入决策主体的记忆和学习机制,将改变观点、保持观点和妥协到中间值三种策略作为博弈方的策略选择,对大型工程复杂大群体动态决策行为进行了研究。 上述研究从研究方法和个体交互特征出发,利用博弈论对二元观点演化模式进行了探究,指出了探究二元观点演化的研究途径和方法,为后续研究提供了一定的启示。然而关于二元观点动力学研究仍存在一定探索空间:首先,现有研究没有结合具体场景,对特定群体的观点演化研究比较缺乏,如医患二元交互与观点演化,电商平台买家卖家观点演化相关研究等。事实上,不同群体的特征其实有所差异,如医患交互对话时,医生由于具有较高的专业素养,丰富的专业知识,因此,医生和患者容易产生信息不对称现象,也即医患观点博弈属于不完全信息博弈,同理,电商平台的买卖家观点交互同样如此。因此,如何将信息不对称考虑到观点交互模型中,也是对现有观点动力学模型进行拓展的一种尝试。其次,现有研究多从模型层面出发,较少从实证研究视角,基于现实生活挖掘个体观点演化机制,由于观点是个体的一种主观态度、想法与思维结晶,会受到个体的心理因素和外部复杂环境的干扰,因此,仅从数值建模层面对观点演化进行研究,难以发掘观点演化的全部特征。如个体在交互过程中,交互的频次、交互的语气、交互的环境、交互的媒介(文本,语音,表情)都可能影响双方观点的演化,借鉴语言学与传播学的相关理论与知识,利用实证研究方法对观点的演化进行研究,也是对现有研究多集中于模型层面的一个补充。 目前,在群体观点演化方面,学者们根据观点的表示形式将观点的动态变化分为离散型和连续型。其中,离散模型通常会将观点赋值为离散的数值,如+1表示赞同,0.5表示中立,-1表示反对。连续型观点演化模型会对观点进行连续取值,如[-1,1]表示观点从反对到赞同的变化。从研究模型来看,现有研究主要对离散和连续观点演化模型进行相关探究。 3.1.1 Ising模型 Ising模型作为离散模型的一种,是一类描述物质相变的随机过程,最初被应用于物理和计算机领域[19]。在Ising模型中,其构成的系统由多维周期性阵点组成,每一个阵点表示一个自旋方向,相邻的阵点之间在一定磁场下可以与其最近的邻居相互作用,进而改变自身的旋向,若自旋方向向上,该点取值为+1,自旋方向向下,该点取值为-1。每个阵点上动力学方程可表示为[20] (1) (2) 其中,kB是玻尔兹曼常数,T是无量纲温度,单位为J/kB。参数T反映了热涨落的影响,T越大,表明节点旋向改变的概率越大。随着Ising模型以及统计物理学的不断发展,学者们逐步将Ising模型应用于社会科学领域,利用节点的旋向表示观点的赞成和反对,积极或者消极等,探究了观点的演化等社会现象。 3.1.2 Sznajd模型 Ising模型根据节点的旋向将观点取值为+1或者-1,Sznajd模型中同样利用Si=+1以及Si=-1表示观点的正反两面[8]。Sznajd模型可以用以下3个步骤进行描述:1)一对相邻的自旋态Si和Si+1将会影响并改变其周围最近的邻居节点Si-1和Si+2;2)如果Si=Si+1,那么Si-1=Si且Si+2=Si;3)如果Si=-Si+1,那么Si-1=Si+1且Si+2=Si。该模型主要借鉴磁场的顺铁和反铁磁性对观点的演化进行类比,反映的主要思想为“团结生存,分化消亡”,最终观点的演化结果为完全一致或者一半一致,一半反对。上述模型为Sznajd一维模型,由于一维模型将维度仅仅限定为一维视角,难以展现现实世界中个体与周围邻居的交互状态,因此,在社会科学中较少使用。Stauffer[21]进一步对一维Sznajd模型进行改进,形成了Sznajd二维模型,Sznajd二维模型演化如图2所示。 3.1.3 Voter模型 Voter模型表示个体受相邻个体的影响,并且从相邻个体中随机选择一个个体的观点作为自身的观点,其观点的演化受周围大多数个体观点演化的影响较小,具体如图3所示。若两节点距离最近,并产生连接,该节点向其周围距离最近节点转化的概率为[22] (3) 此处,ki是节点i的度,也是节点i的最近邻居数,νi即为节点i的邻居。 3.1.4 Majority Vote模型 Majority Vote模型作为一种多数决定少数的模型,在社会生活中得到了广泛应用,在Majority Vote模型中,存在N个节点,每个节点的取值为+1或者-1,节点将根据其周围大多数邻居节点的取值更新自我观点,单位时间内节点值变化概率为[23] (4) (5) 此处,0 3.2.1 DW模型 DW模型作为连续模型的一种,其主要的演化规则为选取群体中任意两个体,若其观点差值|x′-x|≤d,d为信任半径,则该观点将会改变,若大于该阈值,则该观点不会改变。DW模型与HK模型相类似,然而HK模型是个体观点需要与其周围所有个体进行比较,DW模型则是个体观点与其周围个体中的任意一个比较即可。DW模型动力学方程可以表示为 (6) 此处,μ表示收敛参数,其取值范围为[0,0.5]。 3.2.2 HK模型 (7) 此处,aij为观点影响权重,ε为观点影响阈值。DW和HK观点动力学模型均属于连续观点动力学模型,连续观点动力学模型如图5所示。 图4 Galam模型[24] 图5 连续观点动力学模型 从群体观点动力学提出以来,学者们围绕群体观点动力学融合个体交互的新特征对群体动力学模型进行了广泛研究,本文主要从个体特征、行为特征、观点特征、外部环境、观点动力学的应用等方面对观点的演化进行了相关梳理。 个体作为群体中的一员,会在群体观点演化中表现出自身的某些特征,如个体的坚定性、对观点的偏见性和极端性以及个体的知识水平等。在此方面,邓磊和刘云[25]研究了极端个体的建模与观点演化情况,发现社区中的个体观点总具有极端化趋势;杨雷和习鹏[26]以DW模型为例,在考虑群体异质性的基础上,探究了无主见型个体,偏执型个体,以及固执型个体对观点演化的影响,发现不同类型个体的增加将会使群体观点达到一致的步长呈现不同程度的增加;张亮等[27]在DW模型上通过引入个体信息量研究了个体知识水平对舆论传播的影响,发现当信息量服从均匀分布或者幂律分布时,群体认知能力与观点收敛速度成反比,服从正态分布时,认知能力正比于观点收敛速度;邵鹏和胡平[28]从偏执度、影响程度、影响范围界定了粉丝用户、权威用户、大V用户,研究了三类特殊用户对网络群体观点演化的影响,发现特殊用户特征并非直接作用于群体观点形成,而是作为调节变量在特殊用户初始观点与群体平均观点的关系中起到正向或负向调节作用。国外方面,Fu等[29]通过对HK模型进行改进,研究了群体中包含开放型,随和型和封闭型个体情况下观点的动态演化,发现开放型个体观点最容易形成一致,随和型次之,封闭型个体最不容易形成一致观点;Fan和Pedrycz[30]研究了知情个体在观点演化中的作用,发现如果普通个体的初始意见接近于零,知情个体可以在观点演化过程中发挥作用,影响观点的演化,如果普通个体初始时刻有明确的意见,就无法在预先设定的意见上达成充分一致的意见;Xie等[31]研究了群体中含有固执个体的观点演化动态过程,发现固执个体的存在会促使共识的出现;Proskurnikov等[32]对群体中含有偏见个体的观点演化进行了研究,发现偏见个体对观点“锚定”可能会妨碍达成共识,并在社会影响网络中引起分歧。上述研究主要通过改变部分群体观点阈值ε,使得群体内部成员产生异质性(如开放型、随和型和封闭型),进而影响观点的演化结果。若ε较小,该个体则为封闭型,其观点不容易被改变,观点最终结果会比较分散;若ε较大,该个体则为开放型,其观点容易被改变,观点最终结果会比较一致。个体特征视角下的观点演化研究如表3所示。 表3 个体特征视角下的观点演化研究 综上所述,现有研究从个体的坚定性,认知水平,固执性等个体特征视角出发对观点的演化进行了相关研究,这类研究以个体特征为研究对象,通过充分挖掘个体的诸多特性,将这些特性与观点的演化联系起来,为丰富观点动力学研究提供了很好的素材,也为学者们从个体特征视角研究观点动力学开辟了新的视角。 图6 亲和度对舆论观点演化的影响[34] 综上所述,现有研究结合个体在观点演化过程中出现的诸多行为特征对观点的演化进行了相关分析,研究主要基于个体在观点演化过程中所表现出的相关行为,进行提炼和分析,进而找到影响观点演化的相关因素,如个体之间的信任、亲和度、社会相似性、认知失调、篡改行为等,最后将上述因素进行模型化表达。因此,基于个体行为视角,将个体在观点演化过程中表现出的行为特征,考虑到观点演化模型之中,也是当前学界进一步丰富观点动力学模型的一种方法。 在个体表达观点时,部分群体表达的观点处于一个区间之中,是一个不确定值,此外,在观点演化过程中,部分观点信息也可能会相互冲突,学者们对上述情况进行了相关探究。在不确定观点方面,万贻平等[39]探究了个体观点不确定对群体观点多元化的影响,发现观点呈现出类似均匀分布或正态分布时容易形成群体观点多元化,而呈现出“极端子群体”分布时难以形成观点多元化;Zhan等[40]研究了不确定观点在社交网络上的演化,发现初始意见的不确定将会使得群体意见的不确定程度增大,但是随着时间的推进,群体中不确定意见的平均宽度将会小于初始意见的宽度;Cho等[41]通过构建一个主观逻辑(Subjective Logic,SL)观点演化模型,探究了当个体面对冲突信息和不确定信息时,个体意见的演化过程,区别于传统研究利用数值对观点进行表示,该模型从不同维度出发对个体的观点进行了组合定义,利用wi从不同维度对个体的观点进行了表示,wi={bi,di,ui,ai},其中,bi为个体对观点的相信程度,di为个体对观点的不相信程度,ui表示个体对观点的不确定程度,ai表示个体的背景知识;考虑到观点的影响是连续的,陆安和刘业政[42]提出了一种区别于HK模型中观点影响是间断的情形(个体观点之差小于观点影响阈值ε则发生作用,大于ε则不发生作用),提出了一种基于连续影响函数的群体观点演化模型,该模型对现有的观点演化模型进行了一定补充;此外学者们还对观点演化过程中出现的同步现象[43]、收敛速度[44]、意见领袖[45]等现象进行了相关研究。观点特征视角下的观点演化研究如表5所示。 表4 行为特征视角下的观点演化研究 表5 观点特征视角下的观点演化研究 综上所述,现有研究挖掘了观点的不确定性、模糊性、观点冲突等特征,从观点特征视角丰富了观点演化相关结论。对观点特征的挖掘,不仅有利于对个体的观点产生机制有进一步的认识,而且还有利于从不同视角对观点动力学展开研究,未来可进一步在明确观点产生机制上,结合心理学、语言学等多种学科知识,从观点的产生、表达特征、影响特征等多个层面出发,对观点演化模型更为客观地建模。 表6 外部环境视角下的观点演化研究 上述研究将观点演化过程中所面临的外部环境因素纳入到观点演化过程中,构建了考虑外部环境的观点演化动力学模型,研究从个体所处的环境视角对观点动力学模型进行了进一步改进,具有一定的启示意义。在观点演化过程中,基于外部环境视角,若进一步考虑外部压力(群体中包含上级领导)、群体偏好等因素对观点演化的影响,将会使观点动力学模型更为合理地展示现实情况。 部分学者也研究了观点动力学在不同领域内的应用情况。如表7所示,Dou等[52]将Hegselmann-Krause模型引入到产品改进过程中,从观点动力学的角度建立了一个动态模型,研究了不同意见之间的相互作用机制以及意见与产品方案之间的作用机制;林自展等[53]以“大众点评”为例,将观点动力学应用于在线点评,构建了适用于在线点评的观点动力学模型,该模型的提出有助于提高对在线点评观点演化内在机理的深入认识;Wan等[54]提出了一种适用于在线消费者的意见演化动力学模型,该模型可以有效分析消费者的意见随时间的演变情况;雷丽彩等[18]利用观点动力学对大型工程复杂大群体决策的个体观点交互过程和自主博弈行为进行仿真和分析,使得大型工程群体决策管理方法更加贴近项目决策者实际决策心理和行为特征;Gonzalez等[55]提出了一个基于Sznajd模型的选举模型,该模型可应用于选举过程中;此外,部分学者将观点动力学研究成果应用于交通[56]和市场营销[57]等领域。 表7 观点动力学的应用场景 现有研究将观点动力学模型及其演化机理应用于不同的领域之中,使得观点动力学模型的实践价值得以体现。在进行观点动力学研究时,将理论与实践进行结合,不仅有利于创新现有模型,而且还将使得研究更为严谨与可靠,因此,研究者可以基于不同场景,对观点动力学展开研究,这样不仅可以将模型与场景结合起来,而且可以利用应用场景实际数据验证模型的正确性与合理性。未来研究同样可以将观点演化模型应用于假新闻的检测、群体中易感染个体的识别以及推荐系统等领域[3]。 综上所述,现有研究从不同视角出发,对观点的演化进行了大量探索,就观点动力学模型而言,部分学者也利用SJBO模型[58-59]、多智能体模型[60]、贝叶斯网络模型[61]、马尔可夫链模型[62]、网络意见动态模型[63]、社会级联影响模型[64]对观点的演化问题进行了相关研究,这些研究都拓宽了观点动力学研究边界,对后续观点动力学研究具有一定启示意义。 观点作为个体的一种态度、情感与意见,在舆情演化过程中具有重要的地位。对观点的演化进行合理探究对促进舆情合理治理、明确意见演变机理具有重要作用。鉴于当前国内较少研究对观点动力学研究现状进行梳理,本文对国内外现有观点动力学研究现状进行了回顾与梳理,最后对现有研究进行了述评,并对未来研究进行了展望。 现有研究大多基于数值仿真与模拟分析,所使用的数据集往往为随机模拟数据,很少有研究用真实数据进行动力学仿真分析。这使得现有研究缺乏一定的验证过程,难以明晰观点演化的相关作用机理。此外,现有研究虽然已经在观点动力学方面进行了诸多探索,然而在观点的演化方面,仍有较大探索空间,如在群体中含有虚假观点的观点动力学建模方面[2]现有研究较少涉及。现有研究从个体特征、行为特征、观点特征、外部环境对观点动力学进行了诸多有益探索,对观点动力学的建模具有一定的启示意义,然而对观点和意见的强化与争议的消减研究较少。从实践层面来看,对观点演化进行研究,其目的是将研究成果应用于舆情治理、市场营销、公共管理等诸多实践领域中,然而现有的成果却主要集中于观点动力学模型的设计层面,没有对观点演化过程中意见的强化以及争议的消减进行探索,这使得研究成果的实践意义体现较少。现有研究在观点的表示与演化方面进行了相关研究,研究多注重利用数值仿真方法对二元及群体观点的演变进行建模与仿真,对观点与决策之间的作用机制探究较少,这使得观点与决策之间产生了一定研究鸿沟。对观点与决策之间的作用和影响机制进行研究,不仅有利于发掘观点与决策之间的作用路径,而且对弥合观点与决策之间的鸿沟具有重要作用。 观点演化作为一种物理现象和社会行为广泛存在于社会生活中,如何深入挖掘观点和意见的演变机制,对理清清观点作用机理和明确观点演化过程具有重要的理论与实践意义。在观点演化动力学方面,现有研究已经取得了一定的研究进展,然而较少有学者在实证视角下的观点演化机制、意见的强化和争议的消减、观点演化与群体决策的联系等方面进行探究。结合本文研究发现,未来可从以下方向对观点演化进一步探究:1)实证视角下的观点演化机制。现有研究多集中于模型层面,利用随机模拟数据对观点演化进行建模。然而,单一的数理模型方法和随机模拟数据难以揭示观点演化的微观机理[2]。如在二元观点演化过程中,医生和个体的观点如何演化?在线消费者与卖家的观点如何演化?这些问题的解决离不开从实证层面对观点演化进行有效探究,然而现有观点动力学研究对这些问题没有深入探讨。随着海量数据的涌现以及大数据分析技术的不断成熟,利用实证数据和方法对观点的演变机制进行研究成为可能,这对挖掘观点演化机理,构建更加稳健的观点演化模型具有重要理论意义。2)意见的强化和争议的消减”对观点和意见的强化和争议的消减机制进行探究,有利于挖掘观点相互作用机理。在实际生活中,对观点和意见强化以及争议消减进行研究,往往会对解决实践问题如矛盾的消减和积极意见的加强具有重要意义。未来可在明确观点和意见强化以及争议消减机制的基础上,结合语言学、沟通学以及心理学等多种学科知识,构建意见强化和争议消减模型,对意见的强化和争议的消减进行研究,这对解决争议消减如医患对话矛盾以及促使正向舆情传播和演化等相关问题具有一定启示意义。3)观点演化与群体决策的联系。对观点演化与群体决策的作用路径和机制展开研究,有利于弥合观点的演化与决策之间的鸿沟,对建立观点演化与决策之间的联系也具有重要意义[2]。决策存在于生活中的方方面面,尤其离不开人的参与。而观点也是决策过程中存在的一种形式。现有研究多集中于观点的演化,对观点与决策之间的关系探究较少,未来研究可注重探究观点与决策之间的关系,建立观点演化与群体决策之间的联系。如可利用多属性决策和模糊决策方法对群体决策进行建模[65],其表达式可初步写成v=f(a,b,u,w),v表示群体的决策,a表示观点的一致性,b表示专家的权威性,u表示专家的知识水平,w表示专家的偏好。虽然上式给出了观点与群体决策之间的模型表达,然而单就如何衡量群体观点的一致性这一问题,学者们已经进行了大量讨论[66],并且仍在继续探究这一问题。因此,建立观点演化与群体决策的联系,对于解决群体决策问题以及弥合观点与决策之间的关系具有重要的研究价值。
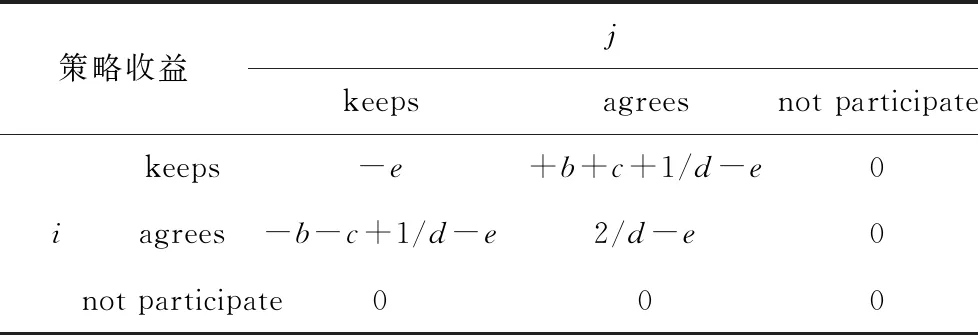
3 群体观点动力学模型
3.1 离散模型
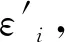
3.2 连续模型



4 群体观点动力学模型研究现状
4.1 个体特征

4.2 行为特征
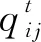
4.3 观点特征

4.4 外部环境

4.5 观点动力学的应用

5 研究述评与展望

