考虑设施可靠性的线状需求物流节点选址研究

周 浩，周建勤

(北京交通大学 经济管理学院，北京 100044)

大型交通线路工程的建设过程中，为更好地解决工程的物资配送问题，需对提供物料供应服务的物流节点进行选址，而所需物料沿着建设线路连续分布，形成与传统的需求离散选址问题不同的线状需求物流节点选址问题。现实中，物流服务设施存在一定的故障概率而中断服务的情况，即设施是不完全可靠的。同时考虑到混凝土类时间敏感型物料作为交通线路建设工程的重要材料，使用量大且对运输时间有一定约束[1]，因此在设施不完全可靠的情况下，对服务时间敏感型物料的物流节点进行选址决策更值得本文探讨。

设施选址问题中，针对需求呈空间连续分布的情形，Domschke等[2]率先将空间连续需求的选址作为单独的一类设施选址问题。Love[3]假定区域内需求均匀分布，构建基于二重积分的选址模型。周建勤[4]提出利用线积分表示物料需求，构建线状需求物流节点选址模型。陈明[5]将一种考虑空间内需求连续分布的集合覆盖模型运用到银行的选址中。计明军等[6]针对长江航道的危险品应急中心进行选址研究，将点状需求的设施选址延伸到线状需求的设施选址领域。但论文最终止步于将整条线路进行分段使线状需求离散化，并没有深入探讨刻画线状需求的方法。

传统设施选址问题一般假设设施是完全可靠的，但在自然灾害、事故灾害、恐怖袭击等其他不可抗力因素下，设施存在故障或损毁的风险。此时，需求就需要距离更远的正常设施来满足，最终总运输成本增加，严重影响整个系统的服务效率和响应能力，最初的选址决策不再适用。Drezner[7]最先研究考虑设施可靠性的选址问题，通过给定一个或多个设施故障的概率拓展了经典p-中值问题。Snyder等[8]研究考虑可靠性的设施选址问题，假设设施中断以相同的概率独立发生，将问题建模为混合整数规划模型，并用拉格朗日松弛法解决。Cui等[9]进一步研究设施故障概率与设施位置相关时的选址决策问题，使模型更加贴近现实情境。Ouyang等[10]、Li等[11-12]将这类选址模型应用于铁路网络缺陷检测系统的部署，提高了给定预算下的总检查效益。Berman等[13]研究客户需求在整个线路上连续均匀分布，设施不完全可靠，且设施间故障概率具有相关性的选址问题，但该问题仅考虑运输成本。本文在此基础上进一步考虑了时间惩罚成本对选址结果的影响。

在选址问题中，针对时间因素的处理，一般有2种方法，分别是将时间作为约束和将时间转化为成本。李延晖等[14]对配送系统中的具有时间约束的单源、p个中转点进行选址研究。Berman等[15]将提供可靠服务的概率设置为客户到设施所需的时间递减函数，解决了在网络上定位多设施，以最大化所有需求点期望服务可靠性的问题。郭毓婷[16]和苏兵等[17]根据时间敏感型产品在运输过程中产品质量呈连续可变的情况，结合配送时间要求，研究以总费用最小为目标的选址问题，但都未考虑设施的可靠性因素对选址结果的影响。

综上所述，已有文献多是针对设施可靠性、需求连续线状和时间约束三者中一种或两种影响因素建立选址的优化模型。本文综合考虑以上3种影响因素，以沿线路连续分布的时间敏感型物料混凝土为需求研究对象，建立总成本最小的可靠性设施选址模型，并证明目标函数在给定区间内为凸函数，利用二次插值和黄金分割相结合的算法求解得到模型的最优解，最后分析设施可靠性以及可靠性间的相关性对选址结果的影响，为复杂情景下的设施选址决策提供较好的参考价值。

1 问题描述和模型假设

1.1 问题描述

本文研究的是铁路线上存在故障概率的混凝土拌和站选址问题。在一段大型线路工程的建设过程中，混凝土物料需求沿建设线路连续分布。而整段线路的需求由位于线路上的2个混凝土拌和站满足，拌和站按照就近原则将混凝土沿线运输至施工区域。考虑自然灾害或人为因素影响，拌和站存在一定的故障概率，当拌和站故障时便丧失所有运力，完全不能提供服务。由于考虑2个设施服务的情形，针对设施的2种运营状态，所以本文共需研究4种问题情形。针对混凝土这类建设物资，除了降低系统的运输成本之外，还要尽量降低物料的运输时间，保证运输至施工区域的混凝土质量。

1.2 模型假设

本文研究一条单位长度的需求线路。假设混凝土需求在线上连续分布，线路上任意点 x的需求密度为 ρ (x) ， x ∈[0,1]。不失一般性假设该线路上需求均匀分布，即ρ (x)=1。2个完全相同混凝土拌和站位于该线路上，为整段线路运输混凝土，考虑拌和站产能足够大忽略其产能限制，整段线路需求都在拌和站的运输能力范围内，且假设单位运输费率为1。用 Xi表 示拌和站在该线段上的位置坐标；i =1,2；X1、 X2∈[0,1]。不失一般性，假设拌和站1位于拌和站2的左边，即0 ≤X1≤X2≤1。

拌和站运营过程中可能会出现故障，本文假设2个拌和站故障的概率都为p ， p ∈(0,1)， 用 p表示拌和站的可靠性，即故障概率 p越大，则拌和站越不可靠。为了简便，下文将2个混凝土拌和站简称为2个设施，参考文献[13]得设施故障的联合概率分布如表1所示。

造成设施故障的自然灾害等涉及空间范围较大，而2个设施位于同一条建设线路上，考虑设施的覆盖范围，与自然灾害涉及的范围相比，其空间距离相距并不远。因此，两设施因自然灾害而故障的概率在空间上呈现一定的正向关性，且两设施的具体选址对其故障概率间相关性影响可忽略不计。同理，其他影响因素导致设施故障概率间相关性为负或者为零的情况类似。综上，为研究方便，本文假设故障概率的相关性与选址的实际位置无关。用r表示2个拌和站故障的相关系数，易得[13]

表1 两设施故障的联合概率分布Table 1 Joint failure probability distribution

由2个拌和站故障的边际概率相同的假设可知p2=p4，则用相关系数 r 和故障概率 p表示2个拌和站可能存在状态的概率为

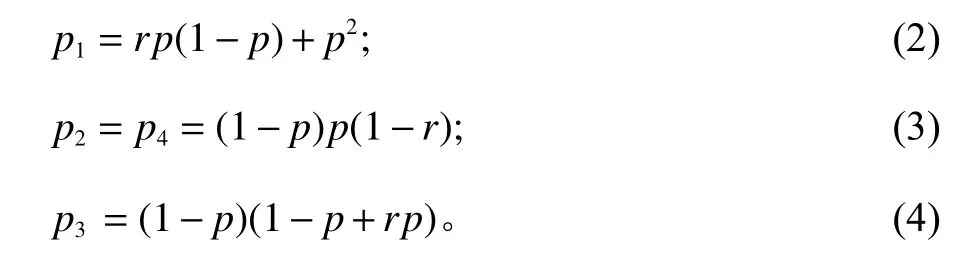
根据文献[18]知，当 (r,p)满足一定相容性，该故障概率的联合分布才有效。则2个拌和站故障的相关系数满足

当设施派出运输车运输混凝土时，必须要考虑混凝土此类时间敏感型物料的运输时间。为了研究方便，本文假设设施的运输车运行平均速度为，则混凝土的运输时间 T 可由运输距离 d来表示，即。本文假设混凝土质量在其可用时间范围内，性能随时间单调递减。

2 模型构建

2.1 距离、需求及运输成本函数

对于位于线上的任意点x ， x ∈[0,1]，其到设施Xi(i ∈{1,2} ) 的距离为直线距离 | Xi−x|。由于服务设施存在一定的故障概率，假设2个设施间为完全信息状态，彼此知道各自位置和运营状态。由文献[19]可知，在本文研究中，为满足2个设施总期望运输距离最短，2个设施负责服务范围的分界点为两设施位置中点。如果两设施都正常运营，则线路上的需求直接由离其最近的设施服务，用 X(x)表示离需求线路上点v 最近的设施，则 X (x)满足

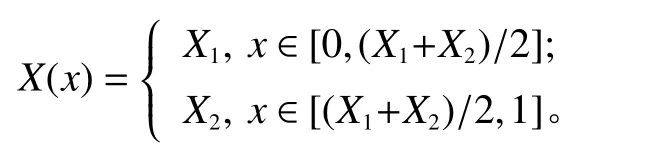
如果只有1个设施故障，则整段线路需求由另一个正常设施服务；如果2个设施都故障，整段线路需求无设施服务，则设施运营商需要受到固定惩罚成本 cf。各种运营状态情况下，为满足 x点需求，设施运行距离及相应惩罚如表2所示。

表2 不同运营状态情况下运行距离及惩罚Table 2 Distance and punishment under different operating conditions

又由 p2=p4，则设施满足需求线路上点v 的期望运输距离为

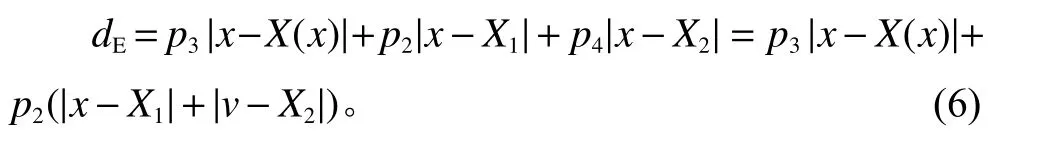
由于线路上需求密度均为 ρ(x)，则线路上某段[x,x+Δx]上 需求可表示为 ρ (x)·Δx。因单位运输费率为1，再根据文献[4]，可考虑物流节点运输费用由物料的需求量、运输的距离和运输费率共同决定，则该段线路需求到服务设施的总期望运输成本可表示为 ρ(x)·Δx·|x−X(x)|。 又由 p2=p4，则2个设施到该段需求线路的运输成本可以表示为

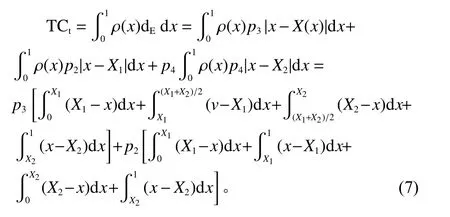
在2个设施同时故障时，系统无运输成本，由表2计算得设施的无服务惩罚成本为定值 p1cf。由分析知， p1cf对线路上设施的选址决策无影响，因此在之后的目标成本函数构成中忽略。

2.2 时间惩罚成本函数

针对混凝土这类随运输时间增加，性能变化幅度较大的建设物资，一般要求运输时间越短越好。而当运输时间增加导致混凝土质量下降时，会产生一定的物料损耗，增加成本。本文研究的是混凝土拌和站的选址问题，因此需要构建关于混凝土期望运输时间的惩罚成本，以保证混凝土质量和选址的总成本最小。根据文献[15]、[16]可知，当物流设施点为所需线路运送混凝土类具有时间敏感型的物料时，可以建立关于运输时间的惩罚成本函数为

在确定的外部条件下， α、 µ为可测、非负的时间敏感系数。

混凝土时间惩罚成本不仅与时间惩罚成本函数有关，而且与需求线路的需求量有关。未满足的需求量越多，惩罚成本便越大，因此时间惩罚成本应该为时间惩罚成本函数与需求量的乘积。则从2个设施到整段需求线路运输混凝土的总惩罚成本为

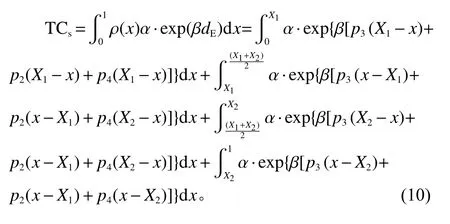
2.3 目标函数及性质分析

本文研究需求线路上仅有2个设施的选址问题，因此在设施数量确定的情况下，设施建设费用和运营费用固定。本文主要以设施承担的物料运输费用、无服务惩罚成本和时间惩罚成本之和最小为目标，根据前文分析知，无服务惩罚成本为定值p1cf，对线路上设施的选址决策无影响，因此在目标成本函数中忽略，即目标函数为

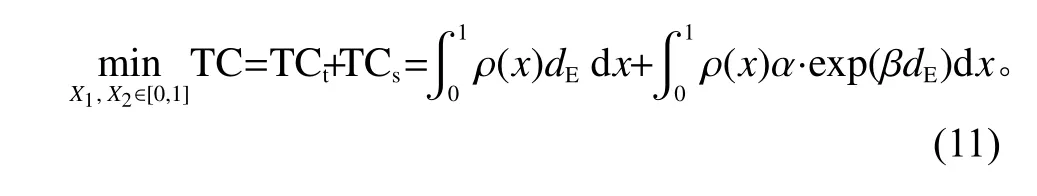
根据模型性质和文献[13]知，该2个设施沿线路中点对称分布，且2个设施都位于单位线段内，则X1+X2=1。 又由假设知 0≤X1≤X2≤1， 所以 X1∈[0,1/2]。

用 X1表 示 X2，计算式(7)和式(10)分别得

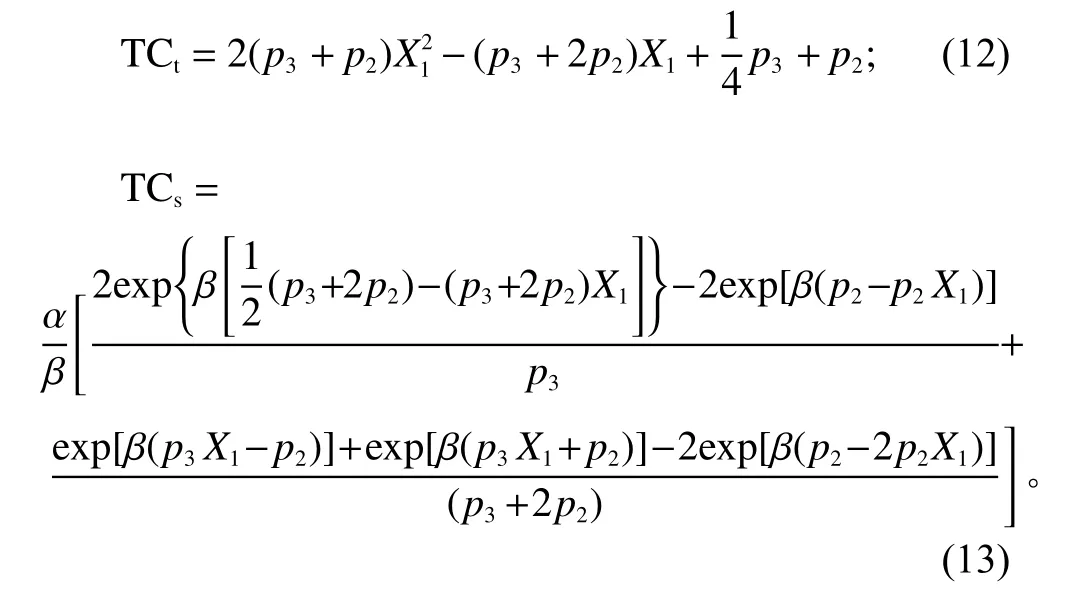
本文旨在研究故障概率p 、概率间相关系数 r以及时间惩罚成本函数中参数 α和 β 对设施选址和目标总成本的影响。则进一步由式(12)和式(13)计算目标函数式(11)，得

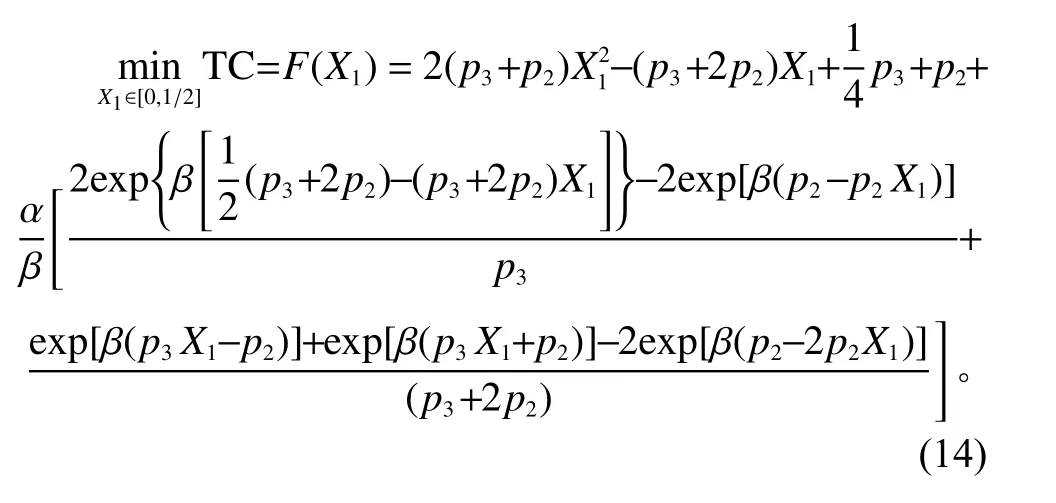
则目标函数关于 X1的一阶导与二阶导分别为

当设施故障概率p 、相关系数 r 给定，可得 p2和p3。在确定的外部条件下，服务时间惩罚成本函数中的参数 α、 β取值也可测得。上述参数给定情况下，可根据式(16)得出目标函数关于 X1的凹凸性再进行求解。

上述参数给定情况下，可知式(17)是关于 X1的超越方程，从而难以给出设施位置最优决策以及最低成本的解析表达式，但可以使用二次插值和黄金分割法相结合的算法进行求解。本文将在算例中通过具体的参数假设，给出设施位置的最优决策以及最低成本随各参数的变化关系。

3 算例求解及模型参数分析

本文的数值计算实验将围绕以下3个方面展开：1) 分析故障概率对两设施选址的影响；2) 分析故障概率间的相关系数对两设施选址和目标成本的影响；3) 分析时间惩罚成本的参数对两设施选址和目标成本的影响。

以建设线路工程的某一直线标段为例，经过实际评估，确定2个拌和站故障的边际概率为 p=0.3，且2个拌和站间故障的相关系数 r=0。根据混凝土产品性质及文献[16]，本算例中设置混凝土运输服务的时间惩罚系数为 α =0.1， β=0.5。在以上给定参数情况下，易证式(16)非负，则目标函数 F(X1)为关于 X1在 X1∈[0,1/2]的凸函数。本文最终建模为一个带约束的单目标最优化问题。

若设施1的最优位置为 X1时，满足目标总成本最小，则有

根据式(17)，可求得设施1最优位置。上述参数给定情况下，式(17)是关于 X1的超越方程，难以给出设施位置最优决策以及最低成本的解析表达式，但根据目标函数F (X1)在 X1∈[0,1/2]区间为凸函数，可利用二次插值和黄金分割法相结合的算法用Matlab R2018b对式(14)进行编码求解，给定容差后求出2个拌和站坐标位置最优决策为(0.324 3，0.675 7)，系统最低成本为0.284 9。由结果可知，即使考虑的设施相同，且服务需求沿线路均匀分布，但由于设施存在一定的故障概率和可靠性服务惩罚成本，设施的最佳选址结果与文献[19]经典的2-median问题的结果，即设施坐标为(1/4, 3/4)，存在明显不同。

3.1 设施故障概率和相关系数对设施选址决策和总成本的影响

以算例中运输混凝土物料为为例，即时间惩罚成本参数 α =0.1， β=0.5时，针对设施故障概率的独立分布，即 r =0， 设施故障概率 p对设施1的最佳位置和系统总成本的影响如图1所示；正负相关系数r下，故障概率 p对2个设施最佳位置的影响如图2所示。

图1 不同故障概率p情况下，设施的最佳位置和最优目标Figure 1 Optimal position and optimal target of the Facility for different probability of failure p

图2 不同相关系数下，设施的最佳位置随故障概率p的变化情况Figure 2 Optimal position of the facility changes with the probability of failure p for different correlation coefficient r

图1 中每个圆圈表示不同 p取值下的设施最佳位置及其对应的最小总成本。对于常规的确定性2-median问题，经典文献[19]给出最优的设施位置为(1/4, 3/4)，与图1中 p=0对应的情况一致，证明模型的合理性。此外，综合图1和图2可知，随着设施故障概率 p的增加，2个设施表现出一种“集中效应”，即随着 p的增加，2个设施不断向彼此移动，更加靠近线段中点。这符合实际情境，即当2个设施的故障概率增加，其可靠性降低时，为了减少总的运输费用和可靠性惩罚成本，设施之间的距离相应减小。由图1可知，随着故障概率 p的增加，目标总成本(TCt+TCs)先增加后减少。这也说明当故障概率在较小范围增大时，系统的运营总成本先是增加的，而当故障概率超过一定的范围，在忽略设施无服务的可靠性惩罚成本 p1cf时，设施的总体运营成本降低。这是因为随着设施故障概率增加，整个系统的可靠性降低，设施因故障而无法服务线路需求的概率增加，因此运输费用和服务可靠性惩罚成本降低的程度逐渐大于因设施位置改变带来的成本增加，因此目标总成本随故障概率先增加后减少。可想而知，当设施故障概率 p=1的极限情况下，设施一直处于故障状态，根本不会产生运输费用和服务可靠性惩罚成本，系统总成本为0。

在现实世界中，许多设施故障的情况表现出强烈的空间相关性。由图2可知，当故障的相关性为正时(例如，由于自然灾害，电网中断)，2个设施同时故障的可能性增加，与故障相关性为0时相比，两设施表现的“集中效应”减弱，为了避免总运营成本增加，相邻的设施倾向于相互靠近的趋势降低。相反，在设施故障概率呈负相关的情况下，彼此相邻的设施更倾向于相互靠近以避免总运营成本增加。同时由图2可知，当故障的相关性为正时，即r=0.3时，满足式(5)，即使在设施故障概率接近1时，2个设施也不会集中在标段中点；而当故障的相关性为负时，即 r =−0.3时，满足式(5)，2个设施在 故障概率接近0.75时就集中在标段中点。

3.2 时间惩罚成本参数对设选址决策和总成本的影响

当设施的故障概率 p=0.3、 相关系数 r=0和固定惩罚成本 p1cf一定时，考虑到设施负责运输的物料的性质不同， α和 β不同取值对设施1最佳位置影响如图3所示，对系统总成本影响如图4所示。图3和图4中数据点为算例所对应的求解结果。

图3 α和β不同取值时设施1的最佳位置Figure 3 Optimal location of facility 1for the different values of α and β

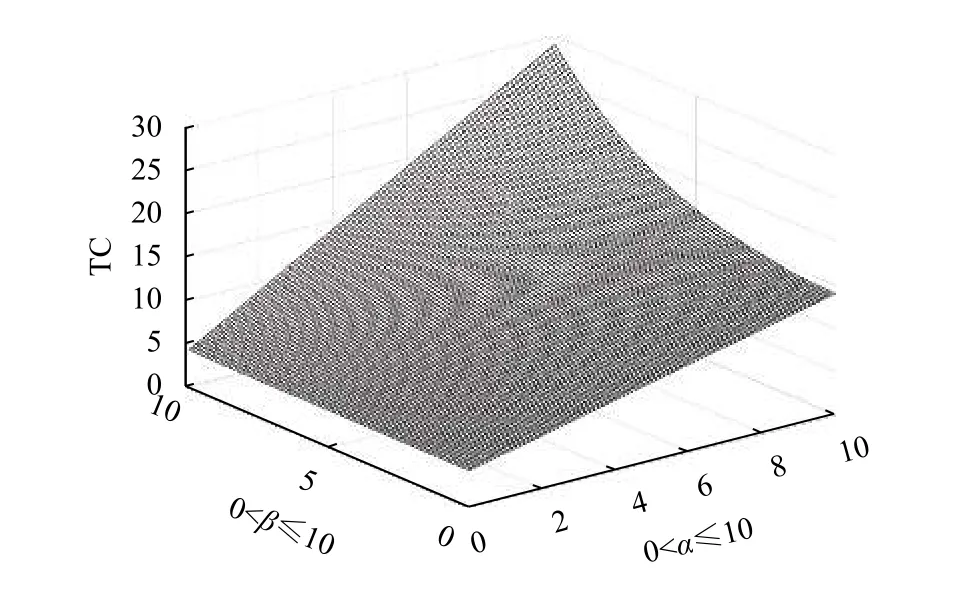
图4 α和β不同取值时目标值的变化Figure 4 Optimal target values changes for different Values of α and β

由图3分析可得，在α 和 β取值范围都为(0,10)时，在刚开始阶段， α和 β的取值对于此参数设置下的2个物流设施点选址的影响很大；在取值都较大时， α和 β的取值对设施点选址的影响程度降低，且在总体的影响过程中，设施1的位置随α /β不同呈现有规律的变化，而 β对设施点选址的影响程度都大于 α。进一步分析得出，负责运输服务可靠性对时间敏感型程度越高物料的设施点位置，更趋向于“去集中效应”，即2个设施彼此背离，设施间距离趋向增加。这定量反映了时间惩罚成本对设施选址的影响增大，同样反映到现实情境中，就是负责运输对时间敏感型程度不同物料的设施选址受到其运输产品性质的影响。由图4可以看出，在 α和 β取值范围都为(0,10)时， α和 β的取值对于此参数设置下的2个物流设施点选址总目标费用的影响不如对设施点位置的影响大，但 β对设施点选址的目标总费用影响程度同样大于α。

4 结束语

针对线状连续需求，本文构建了考虑设施可靠性和时间惩罚的双物流节点选址模型，确定给定故障概率和时间惩罚参数下的选址决策和目标总成本。在经典选址研究基础上，针对问题特性，利用二次插值和黄金分割法相结合的算法用Matlab进行求解。通过算例及模型参数分析，验证本文构建模型的合理性和有效性，分析了故障概率、故障相关性系数、时间惩罚函数参数对设施最佳位置和目标总成本的影响，为线路工程实施企业的可靠性设施选址决策提供辅助决策支持和依据。

针对双设施的选址问题，本文研究设施可靠性之间具有相关性的情况，由于多设施可靠性间具有相关性的选址问题情况较为复杂，所以未来应尝试研究独立故障概率下，连续需求下的多设施选址问题，对双设施选址的研究结果进行拓展分析。