高阶微分方程边值问题正解的存在性

达佳丽， 王 婷， 张丽娟

（西北师范大学知行学院 数学系，甘肃 兰州730070）

本文将利用文献［1］中已有的Green函数，给出它的上下界估计，然后借助不动点指数去讨论（1）式正解的存在性，再利用锥拉伸与压缩不动点定理讨论（2）式存在正解时λ的范围.

1 预备知识

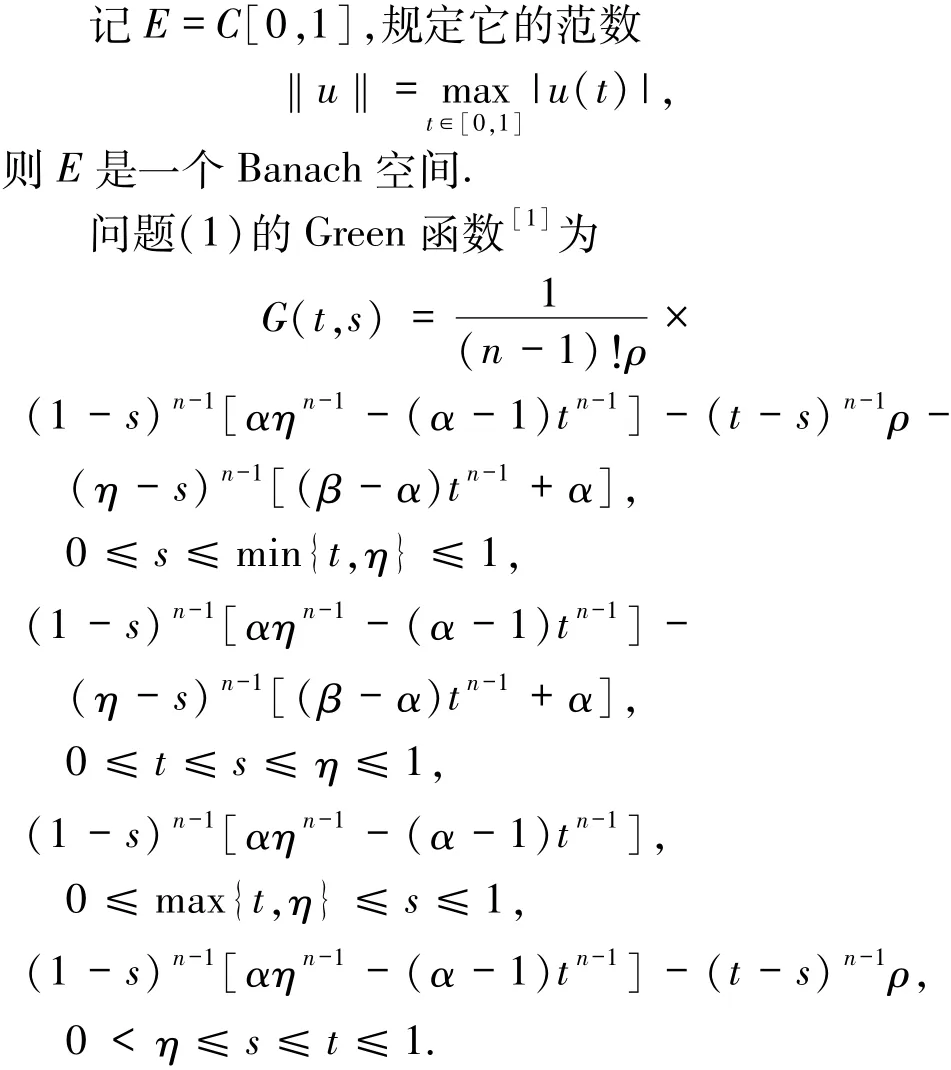
定义算子T：P→P，

本文主要用到推论1.1和推论1.2.

2 主要结果

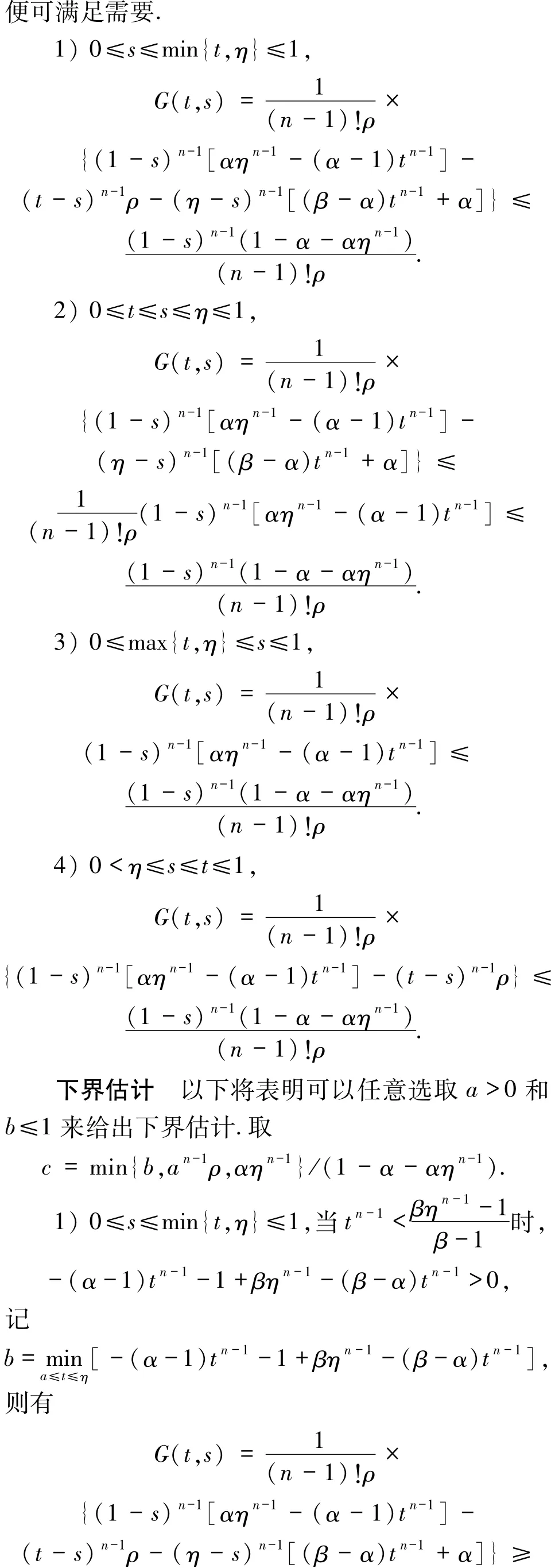
其中η∈（0，1），α，β≥0.参数λ＞0，

应用锥拉伸与压缩不动点定理讨论使得正解存在的λ的范围.

其Green函数为

其中

3 第二部分主要结果及证明

则

故边值问题（2）至少有一个正解.

高阶微分方程解的研究在实际应用中比较广泛，便于对实际问题监控和预测，更多深入系统的研究可以参考文献［3-9］.

致谢 西北师范大学知行学院2019年校级科学研究项目（2019002KA）对本文给予了资助，谨致谢意.