材料中含记忆项的非自治分数阶随机热方程的渐近行为

李林妍， 舒 级， 李 辉， 白欠欠

（四川师范大学 数学科学学院 可视化计算与虚拟现实四川省重点实验室，四川 成都610066）

近十多年来，分数阶微积分理论受到国内外学者的广泛关注，特别是从实际问题抽象出来的分数阶偏微分方程成为大家的研究热点，在化学、物理、生物、人口动力学和金融等领域都有涉及，一些含有分数阶导数的经典数学物理方程能更好地描述复杂现象和复杂系统，包括分数阶Schrödinger方程［1-3］、分 数 阶Landau-Lifshitz方 程［4］、分 数 阶Landau-Lifshitz-Maxwell 方 程［5］、分 数 阶Ginzburg-Landau方程［6-11］和分数阶随机反应扩散方程［12-13］.

研究如下带记忆项的分数阶随机反应扩散方程

其初边值条件分别为

其中，O为R3上带有光滑边界∂O的有界区域，α∈（0，1），ε为正常数，u（x，t）是未知函数，μ是一个非负记忆核，f是非线性项，k（·）∈L2loc（R，L2（O）），h（·）∈H2α，W是概率空间上的双边实值Winner过程.在本文中，u的动力学行为依赖于扩散项过去的历史，即

当α∈（0，1）时，称（-Δ）α为分数阶拉普拉斯算子.在有界区域O上，分数阶拉普拉斯算子有不同的定义，包括积分分数阶拉普拉斯算子和谱分数阶拉普拉斯算子两种定义.当α＝1时，-Δ是标准的拉普拉斯算子.文献［14-19］提出拉回随机吸引子的概念，是确定系统的整体吸引子的推广［20-23］，很好地刻画了随机动力系统的长时间行为.近年来，许多学者已深入研究带有标准拉普拉斯算子的随机方程的随机吸引子，比如自治方程［19，22，24-44］和非自治方程［12，38，45-50］.特别地，文献［51］证明了（1）式的随机吸引子的存在性.当α∈（0，1）时，目前只有几篇文献讨论了随机分数阶偏微分方程解的渐近行为［7，12，52］.注意到，当等［53］用谱分数阶拉普拉斯算子定义证明了方程（1）随机吸引子的存在性.受文献［12，53］的启发，本文将用积分分数阶拉普拉斯算子定义来研究方程（1）在时的随机吸引子的存在性和上半连续性.另外，当有记忆项时，由于包含现象过去的全部历史，不能证明方程（1）产生的随机动力系统的紧性，但是，可以通过分解方法证明其渐近紧性，从而得到紧随机吸收集的存在性.

1 预备知识

最后，为了方便起见，全文用c或者C表示正常数，特别地，用c（·）或C（·）表示与·有关的正常数，这些常数可能不同.

2 随机动力系统

方程（10）-（12）能产生一个连续的随机动力系统.

由于（4）式给出的分数阶拉普拉斯算子（-Δ）α是非局部算子，类似于文献［51］，可将（2）式中条件x∈∂O换为x∈R3＼O，即对α∈（0，1），有

其中非线性函数f满足

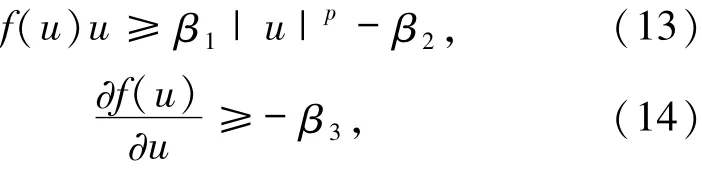
3 随机吸引子

对（46）式右边第一项，由于φτ-t∈D（τ-t，θ-tω）（∈D）及z（ω）是缓增的，于是存在T（τ，ω，D，ε）＞0使得对所有t＞T（τ，ω，D，ε），有

对（46）式右边第二项，由（34）式知

接下来证kε是缓增的，即kε∈D.由（50）式可得

由（35）式可知

又r（ω）及z（ω）均是缓增的，则根据（52）式可得Rε是缓增的，即

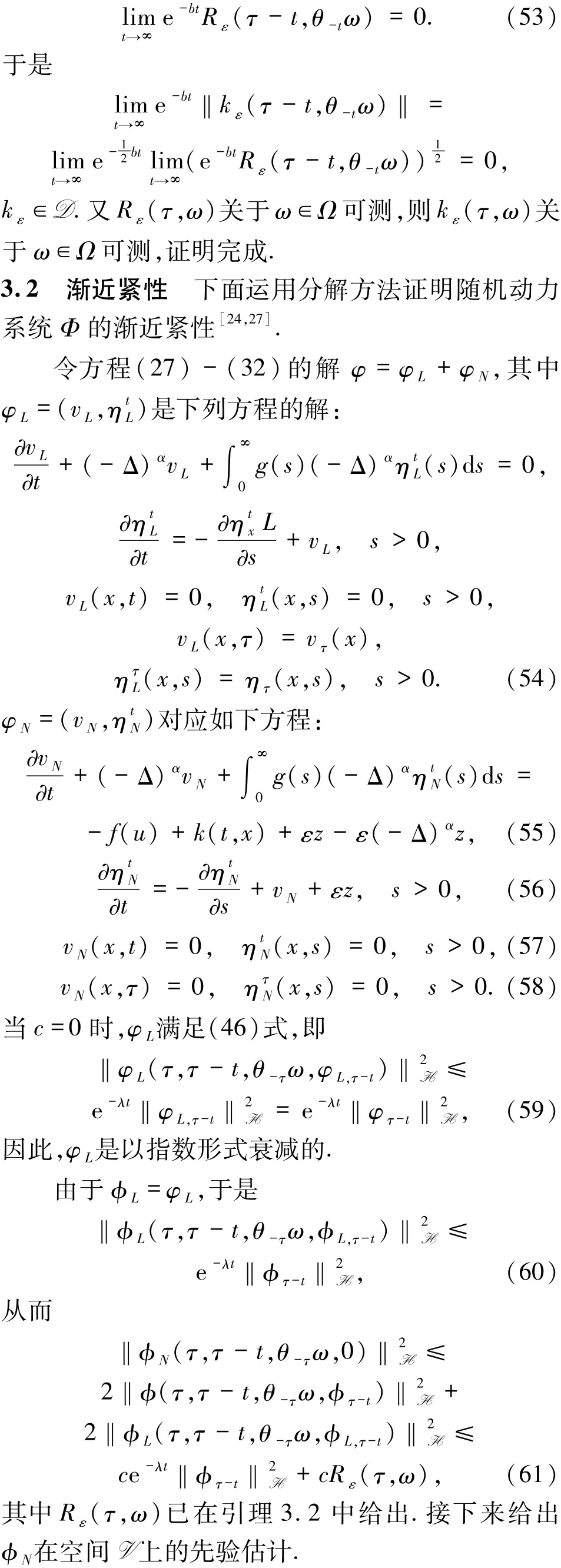
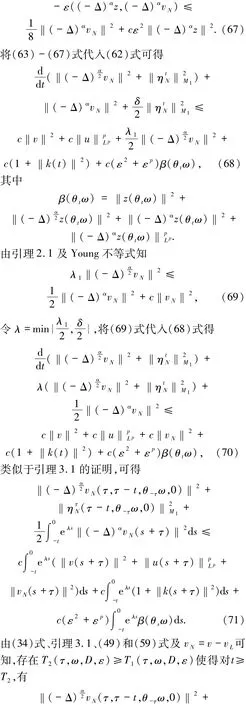
4 上半连续性

由（8）及（88）式得

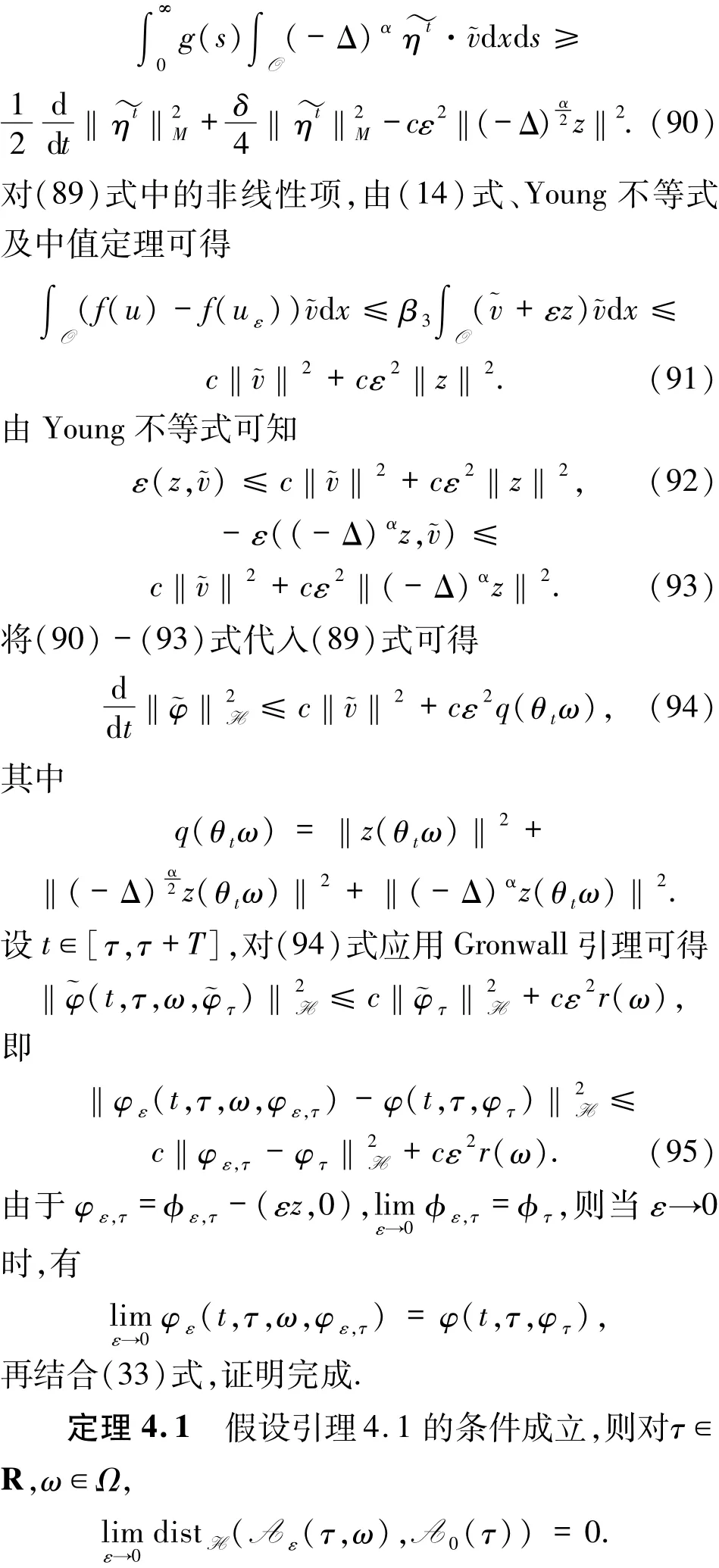
证明 由文献［39］中的定理3.2、（82）和（86）式及引理4.1，结论成立.

致谢 四川师范大学2019年研究生优秀论文培育基金项目（201903-12）和四川省可视化计算与虚拟现实重点实验室对本文予以资助，谨致谢意！