高阶Allen-Cahn系统吸引子的正则性
2021-05-10 02:27潘娇娇
四川师范大学学报(自然科学版) 2021年3期
潘娇娇, 罗 宏
(四川师范大学 数学科学学院,四川 成都610066)
Allen-Cahn方程由文献[1]引入,用于描述微观扩散运动,在反映扩散问题和材料流体动力学中有广泛应用,如图像修复处理[2]、肿瘤生长[3]、随机扰动[4]和晶体模型问题[5-6]等.该方程已有相关研究,Maicon[7]研究了在诺伊曼边界条件下的一维Allen-Cahn方程,证明了解的存在性以及该系统在H1a(0,1)中至少存在一个非常数稳态解.刘桂兰[8]考虑了具有非局部项的Allen-Cahn方程的初边值问题,利用Schauder不动点定理得到了该初边值问题解的存在性.
本文研究高阶Allen-Cahn系统的初边值问题
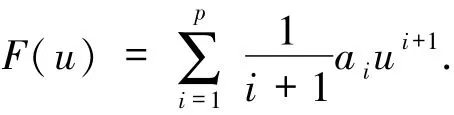
Cherfils等[9]研究了系统(1)在L2(Ω)空间中吸引子的存在性,本文利用算子半群理论和迭代方法研究系统(1)在Hγ(γ>0)空间中全局吸引子的存在性,该方法广泛地应用于数学物理问题[10-13].
1 预备知识


其中Hα=D(Lα)是Lα的定义域.由算子半群理论
可知,对于∀α>β,Hα⊂Hβ是一个紧嵌入.
定义线性算子L:H1→H和非线性算子G:H1→H

2 主要结论





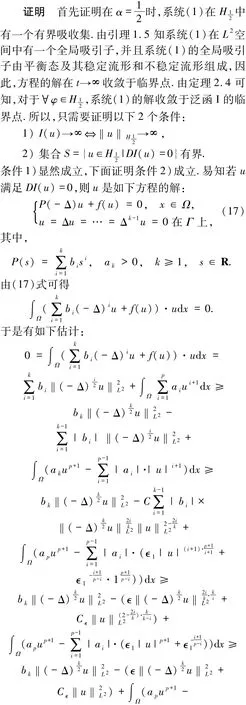

其中,β=α,0<β<1,C>0是与φ无关的常数.使用迭代方法可得‖u(t,φ)‖Hα≤C,α≥0对∀t≥T,φ∈U成立,即对∀α≥0,系统(1)在Hα中存在有界吸收集,定理2.5得证.
最后,由引理1.4、定理2.4和定理2.5可以得到本文的主要定理2.6.
定理2.6 若φ∈Hγ,则系统(1)在空间Hγ(∀γ≥0)中存在全局吸引子.
猜你喜欢
数学物理学报(2022年5期)2022-10-09
数学物理学报(2022年4期)2022-08-22
数学物理学报(2022年1期)2022-03-16
数学物理学报(2021年5期)2021-11-19
数学物理学报(2021年2期)2021-06-09
数学物理学报(2021年1期)2021-03-29
数学物理学报(2021年1期)2021-03-29
哈尔滨轴承(2020年1期)2020-11-03
北京航空航天大学学报(2016年7期)2016-11-16
湖南师范大学学报·自然科学版(2014年3期)2014-10-24

