p阶强度量正则性的扰动稳定性

许文丁， 何诣然

（1.四川师范大学 数学科学学院，四川 成都610066； 2.四川旅游学院 旅游文化产业学院，四川 成都610100）

1 引言及预备知识

定理1.1称为Graves定理.若映射f：X→Y在x¯处严格可微，则由严格可微（不妨设f在x¯处的导数为f′（x¯））的定义可知，对任意ε＞0，存在x¯的邻域U，使得对任意x，x′∈U，有

有

其中记号d（z，A）表示点z到集合A的距离，即

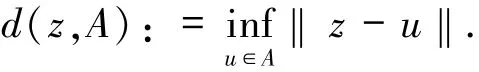
使（1）式成立的所有常数c关于邻域U×V的下确界称为F在x¯处的度量正则模，记为reg F（x¯｜y¯）.F在x¯处度量正则当且仅当reg F（x¯｜y¯）＜∞.

众所周知，对单值映射g：X→Y，常数L≥0，若存在x¯的邻域U，使得对任意x，x′∈U，都有

则称g在x¯处关于常数L局部Lipschitz连续，常数L关于邻域U的下确界称为Lipschitz模，记为Lip（g；x¯）.

由经典的Banach开映像定理可知，连续线性映射A：X→Y是度量正则的当且仅当它是满射.对于非线性映射f：X→Y，文献［1］得到如下结论.

定理1.1 设f：X→Y为映射，A：X→Y为连续线性映射，κ，μ＞0满足κμ＜1.若以下条件成立：

（i）映射A关于常数κ度量正则；

（ii）映射f-A关于常数μ全局Lipschitz连续；

即映射f-f′（x¯）在x¯处是局部Lipschitz连续的，且其Lipschitz常数可以任意小.这样，由定理1.1便容易证得如下推论.

推论1.1 设映射f：X→Y在x¯处严格可微，若其导数为f′（x¯）是满射，则其自身为度量正则的.

事实上，以上推论为充分必要条件，其逆命题的证明可由被称为“推广的Lyusternik-Graves定理”（见文献［2-4］等）所得到.

定理1.2 设κ、μ为2个非负常数满足κμ＜1，F：XY为集值映射，（x¯，y¯）为F的图像上一点，g：X→Y为在x¯处局部Lipschitz连续的单值映射.若F在x¯处度量正则且

同时有

则映射F+g在x¯处度量正则，且

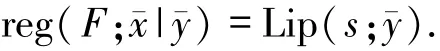
关于强度量正则性，也有以下相应的结论（见文献［3］等）.

定理1.3 设κ、μ为2个非负常数满足κμ＜1，F：X Y为集值映射，（x¯，y¯）为F的图像上一点.g：X→Y为在x¯处局部Lipschizt连续的单值映射.若F在x¯处强度量正则且reg F（x¯｜y¯）≤κ，同时有Lip（g；x¯）≤μ，则映射F+g在x¯处强度量正则，且（2）式成立.

定理1.2与定理1.3说明，（强）度量正则的映射经满足一定条件的Lipschitz映射的扰动后所得映射仍是（强）度量正则的.近几十年来，定理1.2与定理1.3在不同情形下的推广形式被学者们广泛研究和讨论，有兴趣的读者可参见文献［2-9］及其参考文献.下面介绍有关p阶度量正则性的概念及相关结论.

定义1.2 设p＞0为一常数，F：X Y为集值映射，（x¯，y¯）为F的图像上一点.称映射F在x¯处p阶度量正则，如果存在常数c＞0以及x¯与y¯的邻域U和V，使得对任意（x，y）∈U×V，有

使（3）式成立的所有常数c关于邻域U×V的下确界称为F在x¯处的p阶度量正则模，记为regpF（x¯｜y¯）.类似地，F在x¯处p阶度量正则当且仅当

关于p阶度量正则性的扰动稳定性，文献［10］中给出了如下结论（由于本文所涉及的空间均为赋范空间，因此将该结论中的距离空间统一换成赋范空间，距离统一换成范数）.

定理1.4 设X为Banach空间，Y为赋范空间.考虑映射H：＝G+h，其中G：XY为集值映射，h：X→Y为单值映射.设y¯∈G（x¯），常数η＞0.假设：

（i）映射G的图像在（x¯，y¯）处是局部闭的；

（ii）存在c，p＞0，使得对任意（x，y）∈B（x¯，η）×B（y¯，η），有

同时，对任意x，x′∈B（x¯，η），都有

其中k∈（0，c-1p），则存在r＞0，使得满足（4）式的单值映射h称为在处阶Hölder连续，常数k称为h在x¯处的Hölder常数.

定理1.4说明了在一定条件下（度量正则常数与Hölder常数的乘积严格小于1），p阶度量正则的映射经阶Hölder连续的函数扰动后所得函数仍为p阶度量正则的.显然，当p＝1时，定理1.4便退化为定理1.2.

类似于强度量正则性，可以定义如下p阶强度量正则性.

定义1.3 设p＞0为一常数，F：X Y为集值映射，（x¯，y¯）为F的图像上一点.称F在x¯处p阶强度量正则，如果其逆映射F-1在y¯处存在一个p阶Hölder连续的单值局部化，即存在x¯与y¯的邻域U′和V′，使得映射

为单值映射且在y¯处局部p阶Hölder连续.

自然要问，关于强度量正则性的经典扰动稳定性结论（定理1.3），是否也有类似于定理1.4的，推广至p阶情形的结论？本文的主要结论回答了上述问题的答案是肯定的.

2 主要结论

为证明本文的主要结论，需要用到关于p阶Aubin连续性的概念及相关结论（见文献［11-12］）.首先，对于集合A、B，记

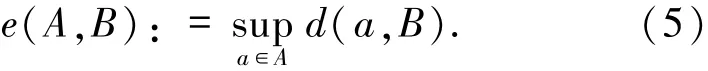
定义2.1 给定常数p＞0，设T：X Y为集值映射，y¯∈T（x¯），且T的图像在（x¯，y¯）处局部闭.称T在x¯处p阶Aubin连续，如果存在常数κ≥0以及x¯的邻域U与y¯的邻域V，使得对任意x′，x∈U，都有

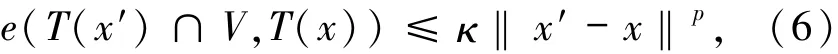
或者，等价地

其中B：＝｛y｜‖y‖≤1｝.使得（6）式成立的所有κ关于邻域U×V的下确界记为Lipp（T；x¯｜y¯）.显然，当映射T取单值时，其在x¯处的p阶Aubin连续性即为p阶Hölder连续性.此时，记Lipp（T；x¯｜T（x¯））为Lipp（T；x¯）.

文献［3］等证明了映射F的度量正则性等价于其逆映射F-1的Aubin连续性.为了证明该等价性可推广至p阶情形［11-12］，首先证明如下引理.

引理2.1 设常数p＞0，点（x¯，y¯）在映射T：X Y的图像上.若T在x¯处p阶Aubin连续，则对于y¯的任一邻域V，存在x¯的邻域U，使得对任意x∈U，有T（x）∩V≠∅.

证明 由映射T在x¯处的Aubin连续性可知，存在x¯的邻域U′与y¯的邻域V′，使得对任意x∈U′，有

于是，对任意x∈U′，有

因此，存在y∈T（x），v∈B，使得

进而有

注意到，对于y¯的任一邻域V，都存在x¯的邻域U，使得U⊂U′，并且对于任意x∈U，有

这样便得到对于任意x∈U，有

引理得证.

对于映射F，其强度量正则性等价于其逆映射F-1具有Aubin连续性且处处不取多值，以下引理说明了该等价性可推广至p阶情形.

引理2.2 设T：X Y为集值映射，y¯∈T（x¯），则下列2个命题等价：

（i）T在x¯周围存在一个以κ为Hölder常数的p阶Hölder连续的单值局部化；

（ii）T在x¯处关于常数κ是p阶Aubin连续的且在x¯处存在一个不取多值的局部化t：X→Y.

证明 （i）⇒（ii）是显然的.下面证明（ii）⇒（i）.

设T在x¯处关于常数κ是p阶Aubin连续的，则由引理2.1可知t为T在x¯周围的一个局部化.因此，存在a，b＞0，使得T（x）∩B（y¯，b）≠∅，并且

为单值映射.取a′＞0使得

这样，对任意x，x′∈B（x¯，a′），都有

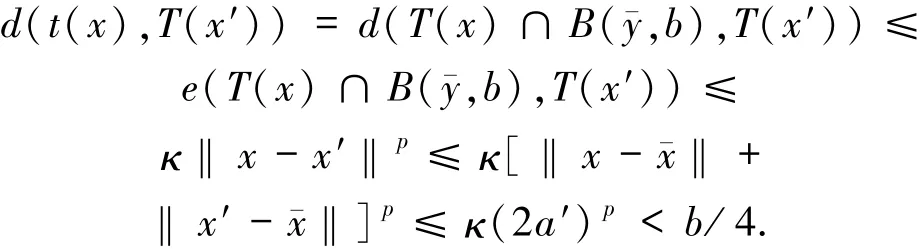
于是，存在y′∈T（x′），使得

由于映射t取单值，故而由t的构造知

于是得到

因此，有y′∈B（y¯，b）.进而

于是可知

即t为T在x¯周围的以κ为常数的p阶Hölder连续的单值局部化.引理得证.

此外，类似于1阶Aubin连续性，p阶Aubin连续性也具有如下性质［3］.

引理2.3 设p＞0为常数，T：XY为集值映射，y¯∈T（x¯），且T的图像在（x¯，y¯）处局部闭，则T在x¯处p阶Aubin连续当且仅当存在x¯的邻域U及y¯的邻域V，使得对任意x′∈X，x∈U，有

证明 若对任意x′∈X，x∈U都有（9）式成立，则由p阶Aubin连续性的定义可知T在x¯处显然是p阶Aubin连续的.

结合（b）并运用定理1.4，可知映射H＝g+F在x¯处p阶度量正则，且

3 结论

本文的主要结论（定理2.3）给出了关于p阶强度量正则性的扰动稳定性结论.该结论指出，p阶强度量正则的集值映射在经阶Hölder连续的单值映射扰动后，所得到的映射仍然是p阶强度量正则的.显然，当p＝1时，定理2.3便退化为经典结果定理1.3.

致谢 四川旅游学院2019年度校级科研项目（19SCTUZZ02）对本文给予了资助，谨致谢意.

定理得证.