应用SARIMA和ETS模型对湖南省肾综合征出血热发病趋势的预测*

哈尔滨医科大学卫生管理学院社会医学与卫生事业管理教研室(150081) 邵瑛琦 刘 欢 李晨希 孟祥伟 李 乐 王 星 吴群红

【提 要】 目的 探讨比较SARIMA模型和ETS模型在湖南省肾综合征出血热的发病预测的应用，为肾综合征出血热的防控提供依据。方法 利用2005-2014年肾综合征出血热月度发病数据建立SARIMA模型和ETS模型，并通过模型预测2015年1～12月的肾综合征出血热发病数，用均方根误差(root mean square error，RMSE)和绝对百分比误差(absolutc percentage error，MAPE)作为评价指标。结果 SARIMA(1，0，0)(3，0，0)12模型是肾综合征出血热发病趋势的最优拟合预测模型，SARIMA模型的MAPE为13.18%，低于ETS模型31.14%，SARIMA模型的RMSE为16.27%也低于ETS模型的25.88%。结论 SARIMA(1，0，0)(3，0，0)12模型模拟拟合效果较好，预测结果可为今后肾综合征出血热的预防和控制提供理论支持。

肾综合征出血热(hemorrhagic fever with renal syndrome，HFRS)是由汉坦病毒(hantaviruses，HV)引起的一种自然疫源性疾病，鼠类为自然宿主和主要传染源，临床表现以高热、腰痛、眼眶痛及肾功能损害为特征[1]。我国是全球HFRS发病最多的国家，累计报告病例占全球病例总数的90%以上[2]。2014年监测结果显示，湖南省为肾综合征出血热高发省份之一，全年发病584人[3]。为了解湖南省HFRS流行特点及未来的流行趋势，本研究通过季节自回归移动平均(seasonal auto regressive integrated moving average，SARIMA)模型和指数平滑模型(exponential smoothing，ETS)对湖南省 HFRS流行趋势进行预测，探讨 SARIMA模型和ETS模型在 HFRS中的预测效果，为湖南省HFRS防控提供科学依据[4]。

资料与方法

1.资料来源

资料来源于公共卫生科学数据中心(http：//www.phsciencedata.cn/)中湖南省HFRS 2005-2015年的月度数据，根据逐月发病数据建立模型，2015年1～12月HFRS逐月发病人数实际值验证模型预测效果。

2.方法

使用Excel 2016建立HFRS数据库，利用R 3.4.2软件。利用R软件对湖南省2005-2015年的HFRS月度发病数据进行处理和分析。选择2005年1月-2015年12月的数据进行建模，通过指数平滑模型ETS和SARIMA模型对2015年发病人数进行预测。

(1)指数平滑模型(ETS)

基于Hyndman等人描述的方法及R软件环境中的预测包建立ETS预测模型。指数平滑法是用序列以往实际观测值的加权平均来预测未来数值，序列中近期的数据赋予较大的权重，远期的数据赋予较小的权重[5]。指数平滑法通过误差(error)、整体趋势(trend)和季节性(seasonal)三个主要参数之间的相加、相乘或无运算进行模型拟合。在参数选择过程中，自动选择ETS模型来拟合具有可乘成分的指数模型，并评估替代模型以选择性能最佳的模型模拟数据。在模型选择过程中，基于赤迟信息准则(Akaike information criterion，AIC)的最小值、校正的Akaike信息准则(the corrected Akaike information criterion，AICc)或贝叶斯信息准则(Bayesian information criterion，BIC)选择最佳模型。Ljung-Box Q检验用于诊断残留错误序列是否为白噪声序列。

(2)季节性自回归综合移动平均模型(SARIMA)

季节性差分自回归滑动平均模型(seasonal autoregressive integrated moving average，SARIMA)建立在差分自回归移动平均模型(autoregressive integrated moving average model，ARIMA)[6]基础上，增加了对季节性和周期性的分析，表达为SARIMA(p，d，q)′(P，D，Q)s，其中p为自回归阶数，d为一般差分阶数，q为移动平均阶数，P为季节性自回归阶数，D为季节性差分阶数，Q为季节性移动平均阶数，s为季节周期[7]。SARIMA(p，q)模型的数学表达式为：Yt=μ+β1Yt-1+β2Yt-2+…+βpYt-p-θ1εt-1-θ2εt-2，-…-θqεq-2+εt。其中Yt是级数的给定值，β和θ是权重，μ是级数的平均值，而εt是预测误差。其中k表示模型中将包括的最大时滞数，而Yt是经过差分后获得的新序列，φ是相应的系数。

本研究使用R 3.4.2软件进行SARIMA 模型的建模，其过程主要包括序列平稳性检验、模型识别、模型的参数估计、模型的检验和优化。①序列样本平稳化检验：通过差分使非平稳时间序列平稳。预测包中的ndiffs函数可用于帮助确定d的最佳值。利用单位根(augmented dickey-fuller，ADF)检验进行平稳化处理。当ADF测试的结果为P<0.05，则证明该序列是稳定的。②模型识别：根据自相关函数(autocorrelation function，ACF)图和偏自相关(partial autocorrelation，PACF)图估算SARIMA模型的参数。③参数估计和检验：利用预测包中的auto.arima函数根据AIC、AICc或BIC中的最小值来选择最佳的SARIMA模型。最后还要对模型的参数进行显著性检验和对残差进行白噪声检验，使用Ljung-Box Q检验来验证估计的残差是否满足白噪声序列的要求，若残差为非白噪声序列，则需要对模型的参数重新估计和拟合。

(3)效果评估指标

采用均方根误差(root mean squared error，RMSE)和绝对百分比误差(mean absolute percentage error，MAPE)2个指标评价ETS和SARIMA模型的拟合、预测效果，其中，2个指标均最小者，拟合(预测)效果最好。

结 果

1.2005年至2015年HFRS报告发病数和时空分布情况

湖南省2005-2015年HFRS月发病情况见表1。基于表1的数据运用R语言中的“decompose”函数分解时间序列的趋势性、季节性和随机误差[8]并绘制时间序列分解图(图1)。时序图显示了2005年1月至2014年12月期间每月的HFRS发病趋势。HFRS发病情况季节特征明显，呈双峰型。春季为HFRS的第一个发病高峰期，随后有短暂的下降趋势，秋季面临一个发病小高峰。2005-2010年与2011-2014年发病人数均呈现出先升高后降低的趋势，发病最高峰为2013年(图1)。

表1 2005-2015年湖南省HFRS逐月发病人数

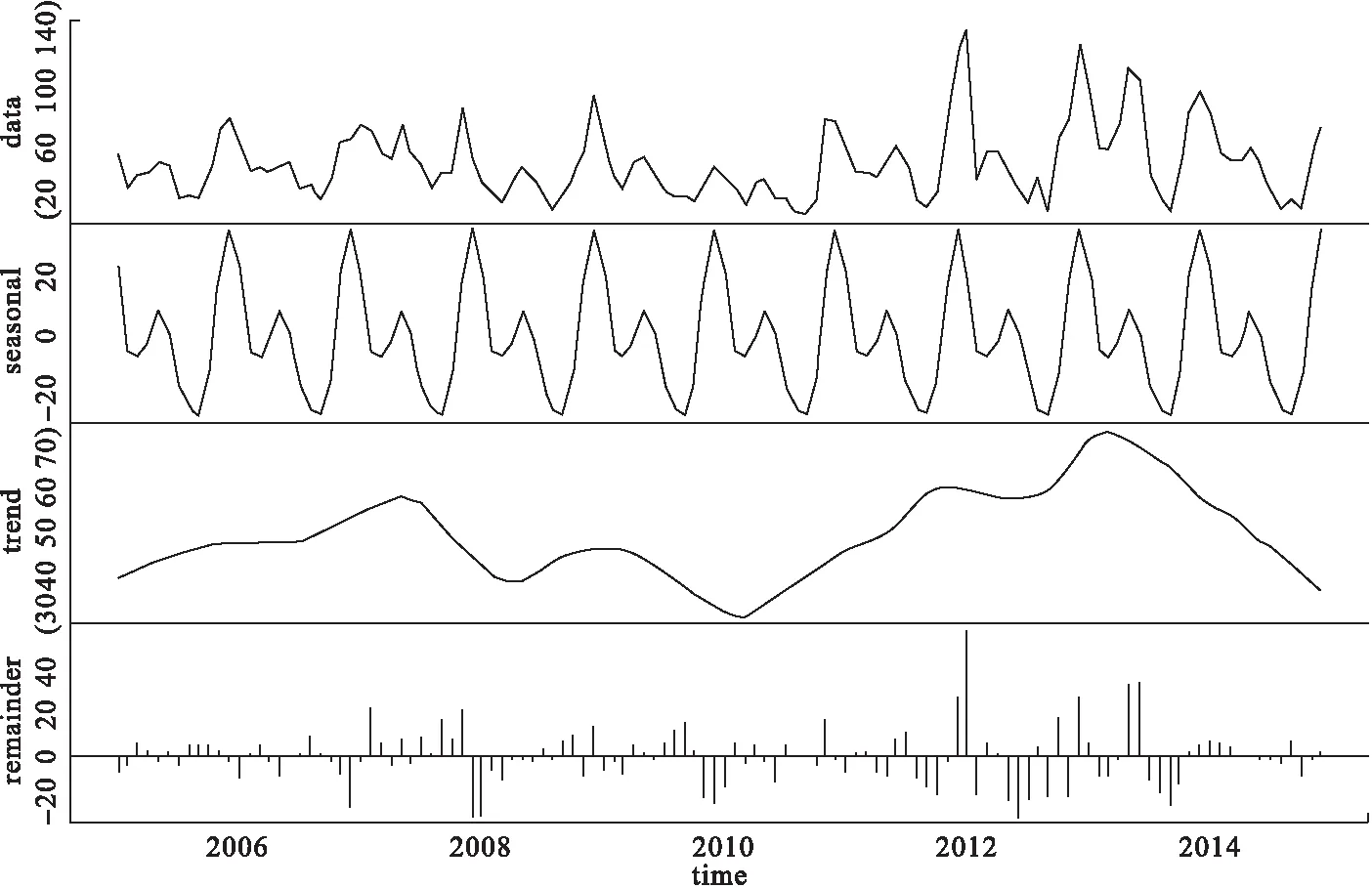
图1 2005年1月至2014年12月湖南省HFRS发病时间序列分解图

2.模型检验与处理

软件中的nddifs代码结果显示HFRS时间序列不需要差分平稳化处理(d=0)。ADF测试结果表明统计学上有意义(P=0.01)，这表明时间序列是稳定的。对模型进行残差检验以估算其他参数，绘制残差序列的自相关(ACF)和偏自相关图(PACF)(图2)。在样本数据中使用时间序列建模器构建SARIMA模型，软件自动选择SARIMA(0，0，1)(3，0，0)12作为最佳拟合模型(AIC=1025.19，BIC=1041.92，AICc=1025.94)。Ljung-Box Q检验进一步表明，残留误差序列包含白噪声(χ2=0.014229，df=1，P=0.905)。在运行ETS代码时，软件自动选择ETS(M，N，M)模型(AIC=1199.165，BIC=1240.977，AICc=1203.780)作为性能最佳的ETS模型。ETS(M，N，M)模型的Ljung-Box Q测试结果表明，残留误差序列也包含白噪声(χ2=0.45363，df=1，P=0.5006)。

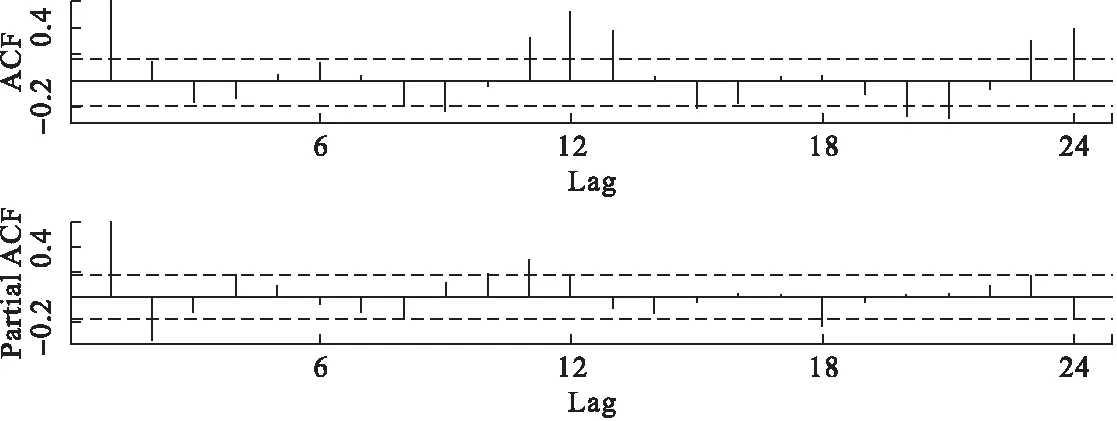
图2 差分HFRS时间序列的自相关和偏自相关图

3.模型预测

运用模型SARIMA(0，0，1)(3，0，0)12和ETS(M，N，M)模型对2015年1月至2015年12月的HFRS疾病逐月发病人数进行回代预测，得到发病人数预测表(表2)和发病趋势图(图3)，结果显示SARIMA模型和EST模型拟合的2015年每月HFRS实际观测发病人数均落入95%的置信区间之内。

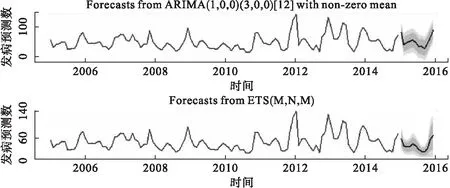
图3 2015年湖南省HFRS发病趋势预测

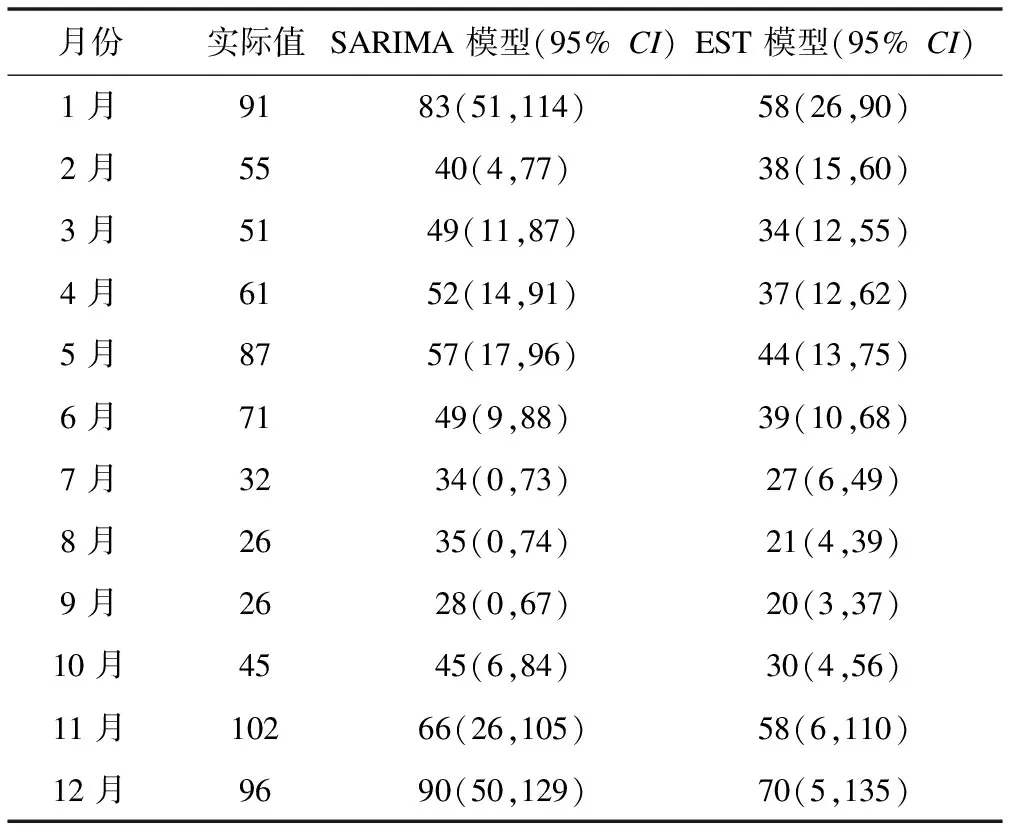
表2 湖南省2015年1～12月HFRS发病人数预测

4.评价拟合效果

SARIMA(1，0，0)(3，0，0)12和ETS(M，N，M)模型的性能度量结果如表3所示。从仿真的两个方面比较两个模型的性能结果表明，SARIMA(1，0，0)(3，0，0)12模型的均方根误差(RMSE)和平均绝对百分比误差(MAPE)均低于ETS(M，N，M)模型。基于湖南省2005年1月-2015年12月短期HFRS预测结果，表明SARIMA模型的预测值与真实值更为吻合，模拟效果较好。

表3 SARIMAM模型、ETS模型与真实值对比

讨 论

传染病具有一定的发病规律，如线性趋势、季节性、周期性等，通过时间序列分析数据探索传染病在时间上的变化规律，能够预测其未来发展趋势[9]。总体来看湖南省HFRS在2005-2015年期间发病表现为上升到下降，再上升至下降的波动状态，HFRS的防控取得了一定的成效，疫情有所缓解，这和相关报道一致[10]。但因存在疫情反复的可能，仍是当前需要重点关注的公共卫生问题[11]。

随着预测理论及预测技术的发展与完善，越来越多的模型被应用于探索传染病的发生规律及预警分析中，SARIMA模型、ETS模型及ARIMA模型均是经典、成熟的时间序列预测方法，也是我国疾病监测工作者应用最为广泛的预测模型[12-13]。而HFRS作为具有典型季节性发病特征的传染病，适用于SARIMA模型，能够弥补既往研究中未纳入HFRS季节性、周期性发病规律的ARIMA预测模型[4，13，16]的不足。ETS模型则利用序列以往实际观测值的加权平均来预测未来数值，兼容全期平均和移动平均的优势，从远到近给予呈指数形式逐渐减弱的权重[14]，同样适用于预测HFRS的发病趋势。本研究分别用SARIMA模型和ETS模型构建湖南省HFRS病例预测模型，从模型的预测结果来看，SARIMA(1，0，0)(3，0，0)12预测结果平均绝对百分比误差为13.18%，ETS模型预测结果平均绝对百分比误差为31.14%，一般认为MAPE低于10%～15%时预测精度较好，SARIMA模型的预测精度要高于ETS模型。原因可能是ETS预测的前提是，历史数据存在的各种因素的影响趋势将持续保持，但是影响肾综合征出血热发病的因素是众多的，当HFRS的发病情况出现上升或下降的趋势时，指数平滑法就难以适应。因此，SARIMA(1，0，0)(3，0，0)12模型更适合用于湖南省HFRS病例发病的短期预测[15]。

本研究所采用的SARIMA模型预测方法虽然较好地模拟和预测了湖南省HFRS发病趋势，但无法揭示引起湖南省HFRS发病变化的各种影响因素[16]，同时所建模型是以历史监测数据序列为依据而建立的，仅适用于短期预测，仍需不断用新的监测数据对所建模型进行修正，并利用多种方法对影响HFRS发病的各种因素展开进一步研究[17]。