一种基于MOVER法中介效应置信区间的构造方法*

南方医科大学公共卫生学院生物统计学系(510515) 杨梓滢 余雯薏 张 玉 周基元

【提 要】 目的 提出一种基于MOVER法中介效应置信区间的构造方法，并与Sobel法、百分位数bootstrap法、偏差校正的百分位数bootstrap法、乘积分布法和Monte Carlo法进行比较。方法 借鉴MOVER法的思想，提出一种新的构造中介效应置信区间的MMA方法。在不同参数设置下，通过计算机模拟，比较MMA法与现有方法的第一类错误率、检验效能、覆盖率及区间宽度。同时，将MMA法与现有方法应用于多发性硬化患者数据，对这些方法做进一步的比较。结果 MMA法在样本量大于25时均能控制第一类错误率，偏差校正的百分位数bootstrap法的第一类错误率可能会膨胀；除了偏差校正的百分位数bootstrap法，MMA法的检验效能明显高于其余方法；随着样本量的增大，MMA法的覆盖率逐渐趋近0.95；在部分模拟背景下，MMA法的区间宽度最窄。结论 MMA法是一种稳健且检验效能有明显提高的中介效应置信区间构造方法。

中介分析广泛应用于心理学[1-2]、流行病学[3-5]等研究领域，其目的不仅要研究自变量和因变量之间的直接关系，还要探索它们之间是否存在中介效应。目前，一般是通过估计中介效应的置信区间进行检验[6]，常用的估计方法有Sobel法[7]、百分位数bootstrap法[8]、偏差校正的百分位数bootstrap法[8]、乘积分布法[9]和Monte Carlo法[10]。其中，偏差校正的百分位数bootstrap法的检验效能最高，然而其第一类错误率可能会膨胀；Sobel法的区间宽度最窄，但其在小样本下的第一类错误率偏保守。因此，有必要提出一种新的中介效应置信区间的构造方法，以提高其检验效能，并缩短其区间宽度[11]。另一方面，Zou等人[12]提出了基于MOVER法(method of variance estimates recovery)构造比值置信区间的方法，该方法是Fieller法[13]的拓展，其基本思想是利用比值中分子、分母的置信区间来构造比值的置信区间。当分子、分母服从偏态分布时，该方法的覆盖率要优于Fieller法，并且估计的区间宽度更窄；当分子、分母都服从正态分布时则与Fieller法等价。因此，本文提出一种基于MOVER法中介效应置信区间的构造方法(MOVER-based mediation analysis，MMA)，并与上述五种方法进行模拟比较，同时将这些方法应用到多发性硬化患者数据[14]，对这些方法做进一步的比较。

原理和方法

考虑如下模型：

Y=β0+cX+e0

(1)

M=β1+aX+e1

(2)

Y=β2+c′X+bM+e2

(3)

其中X、Y与M分别是自变量、因变量与中介变量；β0、β1、β2是截距项；c是X对Y的总效应；ab是X对Y的间接效应；c′是扣除M的影响后X对Y的直接效应；e0、e1、e2是残差。检验中介效应有两种方式[11]，一是检验公式(1)、(3)中回归系数的差c-c′是否为0；二是检验公式(2)、(3)中回归系数的乘积ab是否为0。由于检验前者的第一类错误率通常会膨胀[7，11]，因此在中介分析中一般直接对ab进行检验。

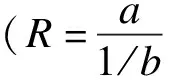
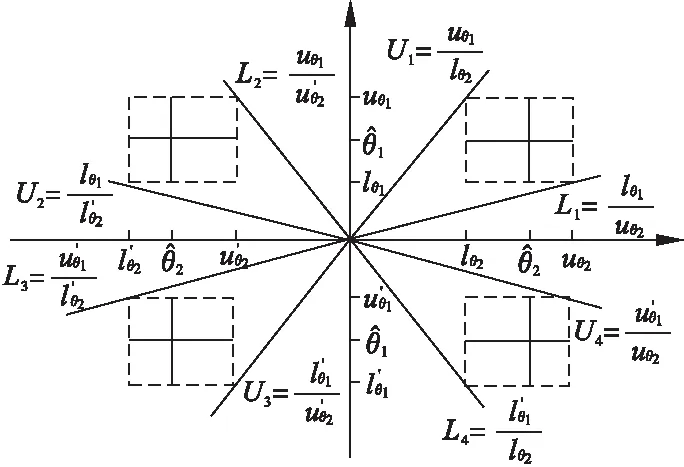
图1 四种情况下比值R的置信区间上、下限取值

(4)

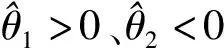
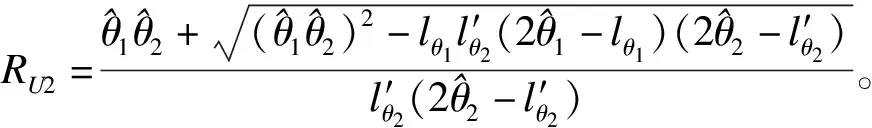
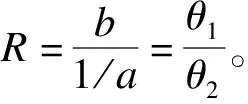
将上述构造中介效应置信区间的方法记为MMA法。

模拟实验

用R语言对新提出的MMA法与现有的Sobel法(Sobel)、百分位数bootstrap法(percentile)、偏差校正的百分位数bootstrap法(BC)、乘积分布法(dop)和Monte Carlo法(MC)在不同样本量(N)、不同中介效应强度(ab)下的第一类错误率、检验效能(power)、覆盖率和区间宽度(width)进行模拟比较。首先从标准正态分布随机抽样分别产生样本量为N的变量X、e1、e2，然后根据公式(2)、(3)计算得到中介变量M和因变量Y。取N=25，50，100，200，500，1000。参照方杰等人的模拟研究[6]，设置三种中介效应为0的参数组合：a=0，b=0；a=0.39，b=0；a=0，b=0.59；设置三种中介效应不为0的参数组合：a=0.14，b=0.14；a=0.39，b=0.39；a=0.59，b=0.59，分别对应中介效应强度为小、中、大的情形。由于MacKinnon等人的模拟研究[7]表明中介分析的模拟结果不受直接效应变化的影响，因此设c′=0。为简化模型，β1、β2也设为0。模拟次数设为1000次，显著性水平设为α=0.05；bootstrap法和Monte Carlo法的重抽样次数分别设为5000次和1000次。

六种方法第一类错误率的模拟结果见表1。由表1知，当a=b=0时，MMA法和其余五种方法的第一类错误率都远低于0.05，且均低于a=0，b≠0与a≠0，b=0情况下的第一类错误率；当a、b中至少有一个不为0时，Sobel法偏保守，偏差校正的百分位数bootstrap法和乘积分布法的第一类错误率可能会膨胀，这与文献[6-7]的研究结果一致。MMA法、百分位数bootstrap法和Monte Carlo法在N>25时能很好地控制第一类错误率。六种方法覆盖率的模拟结果见表2。由表2知，随着样本量和中介效应强度的增大，六种方法的覆盖率逐渐趋于0.95。六种方法检验效能和区间宽度的模拟结果见图2。由图2知，随着样本量和中介效应强度的增大，六种方法的检验效能均逐渐增大。其中偏差校正的百分位数bootstrap法的检验效能最高，MMA法次之。针对区间宽度方面的表现，当N=25时，Sobel法最优；当50≤N≤200时，总的来讲，MMA法最优；N≥500时，Monte Carlo法最优。此外，我们还模拟了a、b至少有一个为负情况下的结果，与上述结果类似，此处不再赘述。

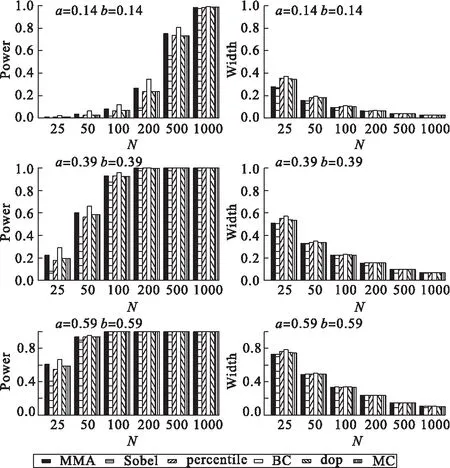
图2 六种方法检验效能和区间宽度的模拟比较

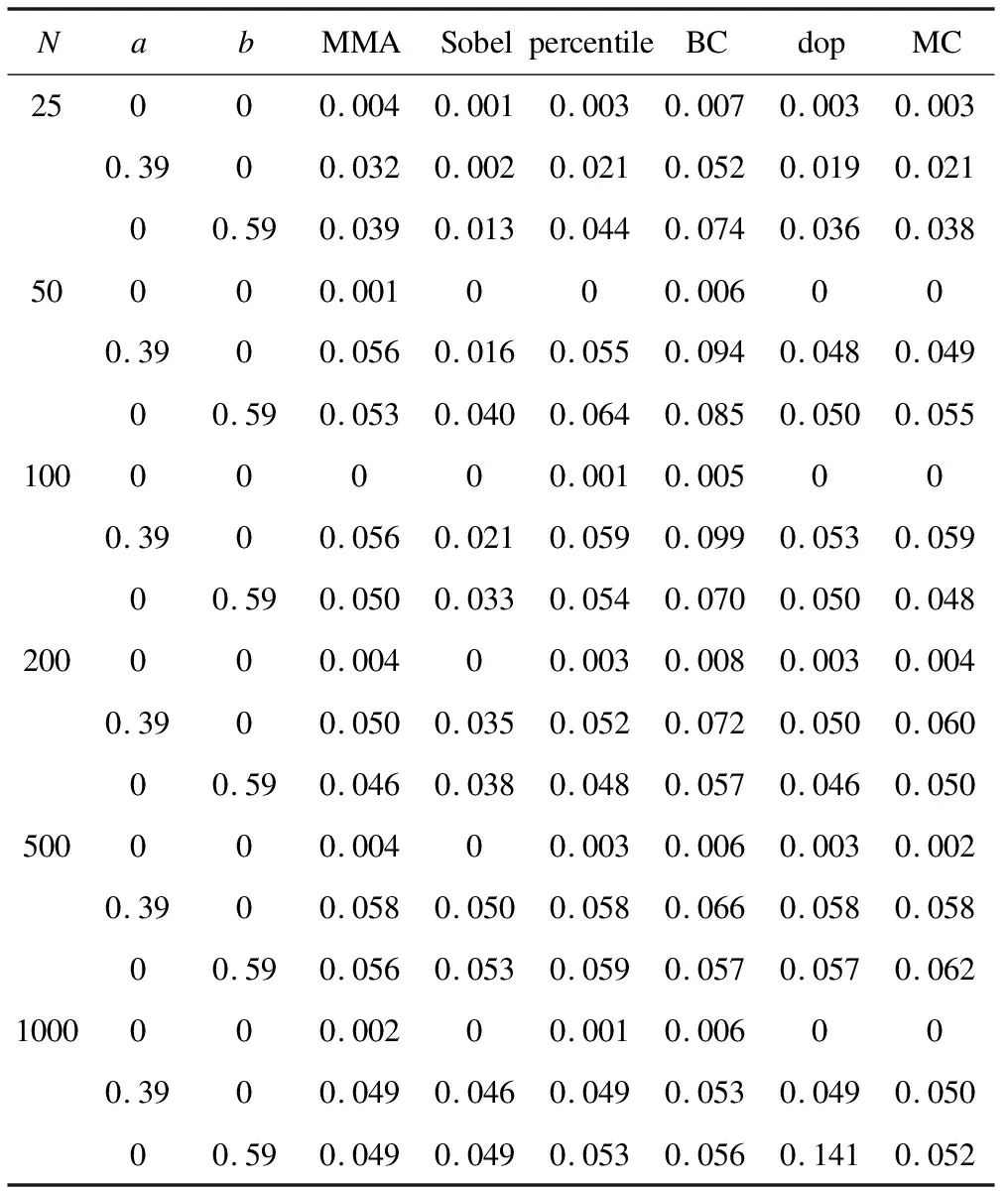
表1 六种方法第一类错误率的模拟比较

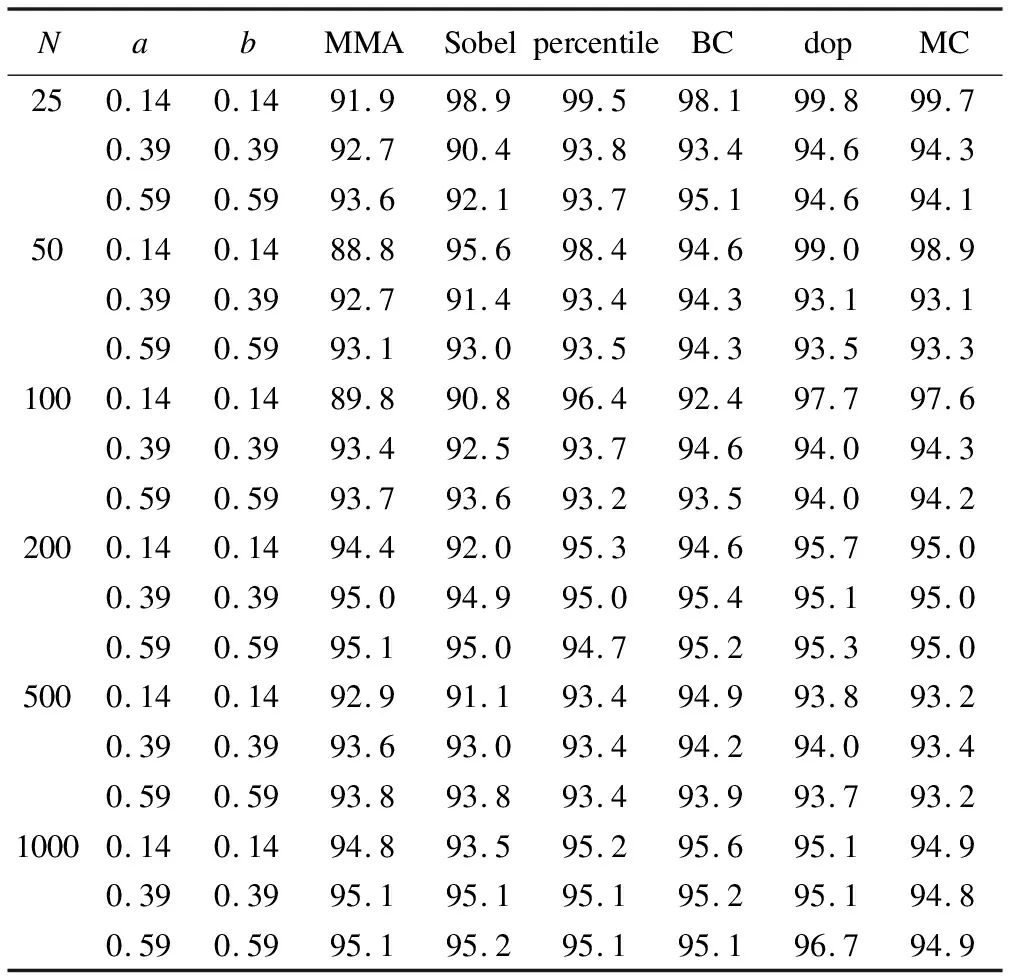
表2 六种方法覆盖率(%)的模拟比较

实例分析

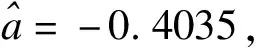
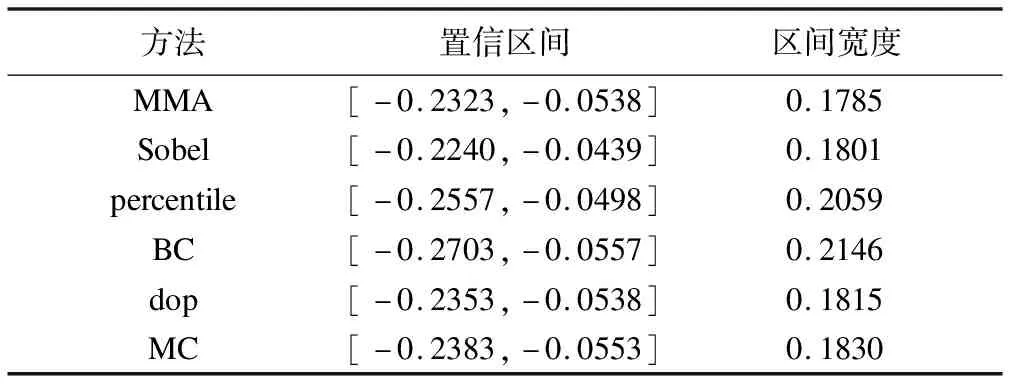
表3 六种方法在实例分析中的中介效应置信区间及区间宽度

讨 论

本文提出了一种基于MOVER法中介效应置信区间的MMA构造方法。模拟结果显示：现有偏差校正的百分位数bootstrap法的检验效能最高，MMA法次之。然而，注意到偏差校正的百分位数bootstrap法的第一类错误率可能会膨胀，其检验效能的结果不一定可靠。另一方面，实例分析结果提示：MMA法的中介效应置信区间的宽度最窄。因此，MMA法是一种稳健、检验效能较高的中介效应置信区间构造方法。此外，本研究仍然存在一些不足。由于新提出的MMA法将中介效应ab转换为比值的形式进行估计，所以当a、b的置信区间都以0为端点、不能取倒数时，无法求解分母的置信区间，因此MMA法不再适用。然而，当a、b的置信区间中至少有一个区间不以0为端点时，即使a、b的置信区间均以0为内点，MMA法仍然适用。另一方面，该方法只考虑了单个中介变量以及因变量仅为计量资料的情况，提示该方法需要向多个中介变量或因变量为计数资料等方向进行拓展，我们将在今后的研究中予以改进。