基于逆重复m序列的岩矿石标本电性参数测量方法研究
程辉, 崔峻卿, 付国红, 傅崧原
1 湖南科技大学先进矿山装备教育部工程研究中心, 湘潭 411201 2 桂林理工大学广西隐伏金属矿产勘查重点实验室, 桂林 541006
0 引言
岩矿石电性参数研究是电法(电磁法)领域的一项重要基础性工作,其研究程度直接影响到方法理论研究与勘查实践工作.众多学者进行了卓有成效的研究工作.Wait(1959a,b)、Madden 和Cantwell(1967)、Ward和Fraser(1976)、Zonge等(1972)、Zonge和Wynn(1975)、Pelton(1977)、Pelton等(1978)、Dias(2000)、Gurin等(2015)、Zhdanov等(2018)、Gurin等(2018)进行了大量露头、标本以及人造标本的测定工作,先后提出了不同的导电机理与导电模型以及相应的参数定义,如阻容模型、德拜模型、瓦尔堡模型、Cole-Cole模型、Dias模型、Gemtip模型等;何继善(2006)、张赛珍等(1984)、王庆乙和徐立忠(2012)、底青云等(2008,2009)、薛国强等(2020)、陈儒军等(2004)、黄理善等(2014)、柯式镇等(2006)、李建军等(2005)、赵云山等(2015)、何兰芳(2014)、程辉等(2010,2014)、付国红等(2020)进行了不同的实验与理论研究工作.
以上研究多是基于变频法进行的频率特性测量,然而,使用变频法观测有着明显不足(何继善,2010):(1)频率改变前后的外部条件与干扰因素各不相同,抗干扰能力相对较弱;(2)各个频点的观测时间不同,观测效率较低且增加了观测数据一致性降低的可能性;(3)为了保证必要的稳流条件,会增加发送端的复杂性.
为了达到实验目的,研究人员使用了各类仪器设备进行观测,包括阻抗分析仪(Solartron 1250、1260,Agilent4294A,HP4263B等)、LCR测试仪(数字电桥测试仪)(ZL5,Hioki 3522-50等)、岩心测试设备(LDT-10发射机与接收机组合形式、GDD公司生产的样本岩芯IP测量仪SCIP等)、激电仪、电化学工作站等.虽然这些观测装置类型不一,但大多是基于变频法思想逐个频点观测.
何继善(2010)以2n序列伪随机波形作为信号源应用于电法勘探,提出了双频激电法与广域电磁法.近年来基于相关辨识的检测技术应用到了电磁法勘探中,赵璧如等(2006)、万健如等(2005)、罗维斌等(2012)、武欣等(2015)、罗延钟等(2015,2020)、王显祥等(2016)、王若等(2016)将m序列(或逆重复m序列)应用于电法勘探中,并进行相应的理论、实验与野外对比观测研究.若将相关辨识技术应用于岩矿石标本电性参数实验,观测数据的抗干扰能力将显著提高,有利于提高测量精度与测量效率.
在针对岩矿石标本的室内电性参数观测工作中,岩矿石标本受其岩性、结构与构造、导电矿物类型与含量及其导电矿物空间分布与接触关系、导电矿物与围岩的接触关系等多方面因素共同影响,即使同一类岩性的标本,在电性参数表现上也可能有数量级的区别.针对观测对象的特殊性与复杂性,一般地,选用频率域信号为激励源进行实验时,有以下要求:(1)实验频带要足够宽;(2)为保证标本的电性参数为线性响应,流过标本的电流激励信号幅值最小仅需维持在10-6A量级;(3)信号源要有较强的负载驱动能力;(4)为了保证观测数据的可靠,要求发送端的电流输出模块必须保证具有较高的输出稳定度.
本文针对以上问题,提出基于逆重复m序列伪随机电流信号的岩矿石标本电性参数观测方案.研发了μA级编码双极性电流源,产生实验所需的高精度小电流,测量频带宽度设置为10-3~104Hz,通过合理改变m序列的编码参数,覆盖整个测量频带,能有效抑制周期性干扰,满足岩矿石标本电性参数观测过程中的特殊要求.文中介绍了逆重复m序列的产生方法与频谱特征,分析了不同阶数序列的测量效率,针对工频干扰提出编码参数选择要求;围绕岩矿石标本电性特征,从观测装置角度论述了发送端驱动能力及接收端阻抗匹配、相关辨识法校正测试系统频率响应以及高频微弱电流信号的产生与拾取等关键技术问题,并对所研发的电流源进行了实验验证.
1 逆重复m序列的产生及其频谱特征
1.1 逆重复m序列伪随机信号的产生
逆重复m序列是将 2 个周期的m序列隔位取反后得到的一种伪随机序列,并且与m序列互不相关.因此由m序列可方便得到逆重复m序列.
m序列伪随机信号在电法勘探中采用二进制、双极性的信号形式,n阶m序列的周期长度为N=2n-1.m序列可由n级线性反馈移位寄存器生成,也可使用线性递推公式产生:
ai=p1ai-1⊕p2ai-2⊕…⊕pnai-n,i≥0,
(1)
式中,⊕表示异或运算,pi为n阶m序列的本原多项式系数.表1列出部分阶数m序列的递推公式.

表1 递推公式表Table 1 Recursive formula
令初始条件a-1,a-2,…,a-n不全为 0 (一般取初始条件全为 1),则m序列{ai} 可通过式(1)获得.通过映射关系:
(2)
使用周期为Δt的时钟控制ui输出,则可获得双极性m序列伪随机信号,周期为T=NΔt=N/fc(fc=1/Δt,为码元频率).同样地对逆重复m序列进行处理,可得到周期为2T的逆重复m序列伪随机信号L(t),图1为fc=3.1 Hz的5阶L(t)波形图.

图1 5阶L(t)伪随机信号波形(fc=3.1 Hz)Fig.1 Waveforms of 5th-order L(t) pseudo-random singal (fc=3.1 Hz)
1.2 逆重复m序列的频谱特征
L(t)属于循环平稳随机过程,其自相关函数为(钟延炯,1979):
RLL(τ)=
(3)
其中:
式(3)中第一项为三角脉冲函数,第二项为周期三角波函数,其自相关函数为三角脉冲函数与周期三角波之和,归一化自相关函数图如图2a所示.由式(3)中各项的系数可知,阶数n越大,周期长度N越大,周期三角波的幅值越小,自相关函数越接近脉冲函数,辨识误差越小.因此选取适当大的阶数n,可以提高辨识精度.
根据维纳—辛钦定理,将L(t)的自相关函数RLL(τ)进行傅里叶变换即可得到L(t)的功率谱:

(4)
将式(3)代入式(4),求得:

(5)
考察函数 sinc(f/fc),令sinc(f/fc)=1/2,求得f≈0.44fc,即 -3 dB带宽截止频率.
(6)


图2 5阶L(t)自相关函数图(a)及理论功率谱图(b)Fig.2 The 5th-order L(t)-signal autocorrelation function (a) and theoretical power spectrum (b)
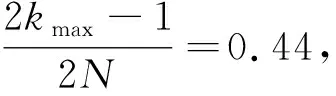
kmax=0.44(2n-1)+0.5,
(7)
式中,kmax向左取整.
(8)
L(t)的周期公式为:
(9)
因此两种方法所用时间之比为:
(10)
根据式(10)可知,测量效率与阶数n有关,n越大,测量效率提升越明显,表2列出了部分阶数序列对应的测量频点个数以及测量效率提高的倍数.
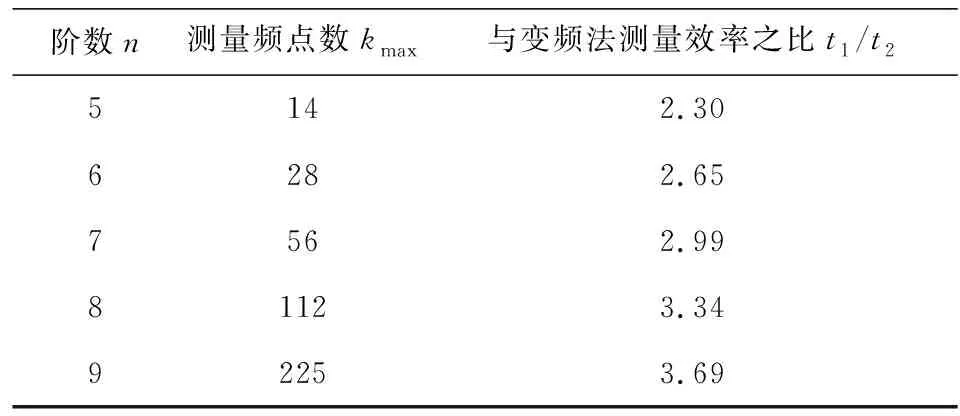
表2 不同阶数L序列测量效率表Table 2 Efficiency of L-sequence measurement with different orders
2 抗工频干扰参数选取条件
岩矿石频谱测量工作中观测数据受自身固有特性、外部因素、溶液条件、仪器和实验条件的共同作用,从干扰类型与强度分析,工频干扰最为明显且难以屏蔽.由于L(t)具有良好的自相关性,通过合理选择编码参数,可以使工频干扰信号正交于L(t),从而通过相关辨识的方法压制工频干扰.
工频干扰为典型的周期性干扰信号,在接收端表现为L(t)经过岩矿石标本后的响应信号与干扰信号叠加.设周期干扰信号n(t)=Acos(ω0t+φ),周期为T0=2π/ω0,其自相关函数为:
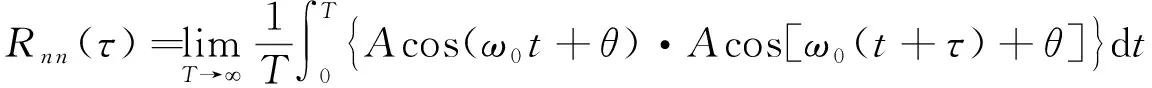
(11)
功率谱为:
Sn n(ω)=F[Rn n(τ)]
(12)
(13)
式中,f0=1/T0,其自功率谱也是离散谱,只在±f0处取值.设两信号的互功率谱为SLn(f),则有不等式:

(14)

RLn(τ)=F-1[SLn(f)]=0.
(15)
因此,当L(t)信号中不包含工频频率分量时,其与工频干扰的互相关函数为0,可以有效压制工频干扰.考虑到实际测量过程中存在工频干扰频率偏移等问题,在选取码元频率fc时,可根据实际工作条件,避开工频干扰的频率.
图3为抑制工频干扰效果仿真图,L(t)参数为:fc=2000 Hz,n=7,在50 Hz附近的频点为39.37 Hz和55.12 Hz,波形如图3a.经过图10所示的系统后,输出响应为图3b.引入信噪比为-20 dB的50 Hz干扰信号后,输出响应如图3c.未被干扰信号和被干扰信号的辨识结果如图3d,两曲线基本吻合,50 Hz附近无明显波动,按照此要求选择频组,具有良好的工频干扰抑制效果.

图3 工频干扰压制仿真(a) 系统输入信号; (b) 系统输出响应; (c) 被50 Hz干扰的输出响应; (d) 测得系统频率响应对比.Fig.3 Suppression simulation of power frequency interference(a) System input signal; (b) System output response; (c) Output response disturbed by 50 Hz; (d) Comparison of measured system frequency responses.
3 观测系统精细测量的解决方法
在实现精准的测量过程中,面临电阻率分布跨度大、频率响应存在观测误差大、频率分布范围宽等问题,在开展被测对象特征的研究基础上,确定观测系统精细测量的解决方法.
针对岩矿石标本电阻率分布跨度大(n×10~106Ωm),采用高驱动能力设计及阻抗匹配技术;针对频率响应存在观测误差,采用系统频率响应校正技术;针对频率分布范围宽(10-3~104Hz)以及非线性效应问题,采用高频微弱信号产生与拾取的相关技术.图4为观测系统示意图,由发送机产生逆重复m序列电流信号,作为待测标本的激励源,使用数据采集卡采集标本响应.

图4 观测系统示意图Fig.4 Schematic diagram of the observation system

图5 激发极化效应等效电路(a)及恒流源供电示意图(b)Fig.5 Equivalent circuit of IP effect (a) and power supply of constant current source (b)
3.1 发送端驱动能力及接收端阻抗匹配问题
岩矿石标本电阻率可达n×106Ωm,以长l为5 cm,半径r为2 cm的标准圆柱体标本为例,其直流阻值约为n×39.8 MΩ.W.H.Pelton经过对岩矿石的大量实验和研究,提出岩矿石激发极化效应可以等效为图5a的等效电路.
此模型复阻抗可由式(16)计算得到:
(16)

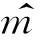
恒流信号源通常采用压控电流源的方式实现,其驱动能力主要受限于最高输出电压,原理如图5b所示.恒流源输出恒定电流,当负载RL发生变化时,输出电压UO亦随负载变化.实际器件输出电压受供电电源限制,当负载足够大时,输出电压达到最大值,此时恒流源将输出恒定电压,反馈回路失效,类似于恒压源,电流将随负载变大而减小,输出信号将严重失真.另一方面,在频率较高时,过大的负载将与线路间的杂散分布电容CP形成RC网络,使τ值变大,导致输出波形上升沿平缓,增大测量误差.

图6 测量回路阻抗等效电路Fig.6 Measurement circuit impedance equivalent circuit
对于接收端而言,测量回路阻抗等效电路如图6所示,实际测得阻抗为负载RL与测量系统输入阻抗Rin的并联阻抗,测量时必须加以考虑.
因此在系统设计时,发送端要保证较高的输出电压范围,选用高带宽、高压摆率的运放器件,并尽量降低回路分布电容,以扩大测量负载范围,提高频率响应范围.接收端应采用差分输入模式,并设置几组不同的输入阻抗,根据负载阻抗大小合理切换,在保证测量精度的前提下,保持较高的信噪比.
3.2 系统频率响应校正
在实际工作中,尽管测试系统采用高性能器件,但系统频率响应误差仍然存在且不可避免.下面根据相关辨识测量原理,给出系统频率响应误差校正方法.相关辨识测量原理如图7所示,L(t) 经过测试系统H′(ω)后,引入干扰信号e(t),最终测得输出信号y(t).然后将y(t)与L(t)通过前文第一小节的方法,分别计算出互功率谱和自功率谱并相除,即可求得系统响应H′(f).

图7 相关辨识原理图Fig.7 Schematic diagram of correlation identification
测试系统H′(ω)简化框图如图8所示.信号L(t)经过发送通道的V-I转换后变为电流型激励信号,激发标本产生响应,后经接收端测量通道进行采集,记录为时间序列y[n].

图8 测量系统信号传递框图Fig.8 Signal transmission block diagram of the measuring system
对测得数据处理后,得到的系统响应为发送通道响应h0(t)、标本响应h(t)和测量通道响应h1(t)共同作用的结果,最终测得系统频率响应H′(ω)可用式(17)表示:
(17)
其中,H0(ω)、H(ω)、H1(ω)分别对应图7中各部分的频率响应,X(ω)、Y(ω)为系统输入输出采样信号x[n]、y[n]的傅里叶变换.由式(18)可得标本真实频率响应的修正公式:
(18)
根据式(18)可知,采用标准电阻作为负载,测得系统频率响应即可修正误差.
3.3 避免非线性效应的高频弱信号产生及拾取
对于岩矿石的非线性效应,何继善等(1995)提出不同矿物出现非线性特征所需的电流密度不同,最小仅1 μA/cm2,因此发送信号的电流幅值需实现μA级稳定输出.本文提出的观测方法,所用信号采用双极性形式,且码元频率fc是测量带宽上限频率的2.23倍,逆变频率至少应达到22.3 kHz.微弱电流的高速逆变,不仅要保证电流的直流输出精度,还要保证高频时电流不会因寄生感抗而衰减,实现较为困难.经过研究与多次试验,采用图9所示的运放级联技术,实现了设计要求.输入级采用带宽尽量高的精密运放(对应图9中的A1、A3),输出级采用高速运放(对应图9中的A2),保证精度与带宽.输入信号Uin为电压信号L(t),经过运放电路实现电压-电流转换,将电压信号转换为电流信号输出.输出电流信号幅值由输入信号幅值决定,通过调节输入端电压信号幅值获得不同输出电流幅值.

图9 恒流源级联原理示意图Fig.9 Schematic diagram of the flow source cascade
接收端采集的信号是电压信号,在测量低阻标本时,电压通常只有n×100 μV,因此测量端至少需要保证0.1 μV测量分辨率.根据采样定理,采样频率至少为44.6 kHz才能保证频率不失真.在室内环境中,工频干扰耦合在测量回路中的幅值可达几十毫伏,为了提高测量信噪比,在分辨率足够的前提下,可在测量回路中串联精密电阻提高输出响应幅值,再根据基尔霍夫电压定理(KVL)校正为标本响应.
4 实验测试
为验证方法的可行性与设计仪器的性能,实验分别对所研发电流源样机的直流恒流性能和交流测量精度进行测试,根据本文提出的测量方法,研制了信号发送样机,电路板实物图如图10所示,采用NI公司的NI-PXIe4497数据采集卡采集数据,最大采样率为204.8 kS/s,具有24位A/D转换精度.

图10 样机电路板实物图Fig.10 Real object diagram of prototype circuit board
直流恒流性能选取输出电流幅值为2 μA,依次使用阻值为100 Ω、1 kΩ、10 kΩ、100 kΩ、1 MΩ的电阻作为负载,采用电流-电压(I-V)转换增益为104的I-V转换电路,测量I-V转换电路的输出电压,测量结果如图11所示.在不同负载下,电流输出稳定度较高,整体波动范围小于0.5%.从图11中可以看到,在高阻负载情况下输出电流偏低,是因为电阻存在制造公差,导致恒流源V-I转换电路的反馈回路电阻阻值不严格匹配,可经过调试进一步降低误差,获取更高的输出稳定度.

图11 不同负载的稳定性Fig.11 Stability under different loads
交流精度测试采用阻容模型模拟岩矿石标本,图12给出了测量所用阻容模型及其幅频特性曲线.

图12 阻容模型及其幅频特性Fig.12 Resistive and capacitive model and amplitude-frequency characteristics

图13 转折频率附近频组响应波形及功率谱(a) (e) fc=62 Hz; (b) (f) fc=625 Hz; (c) (g) fc=6.25 kHz; (d) (h) fc=62 kHz.Fig.13 Response waveforms of the frequency group near the turning frequency and power spectrum
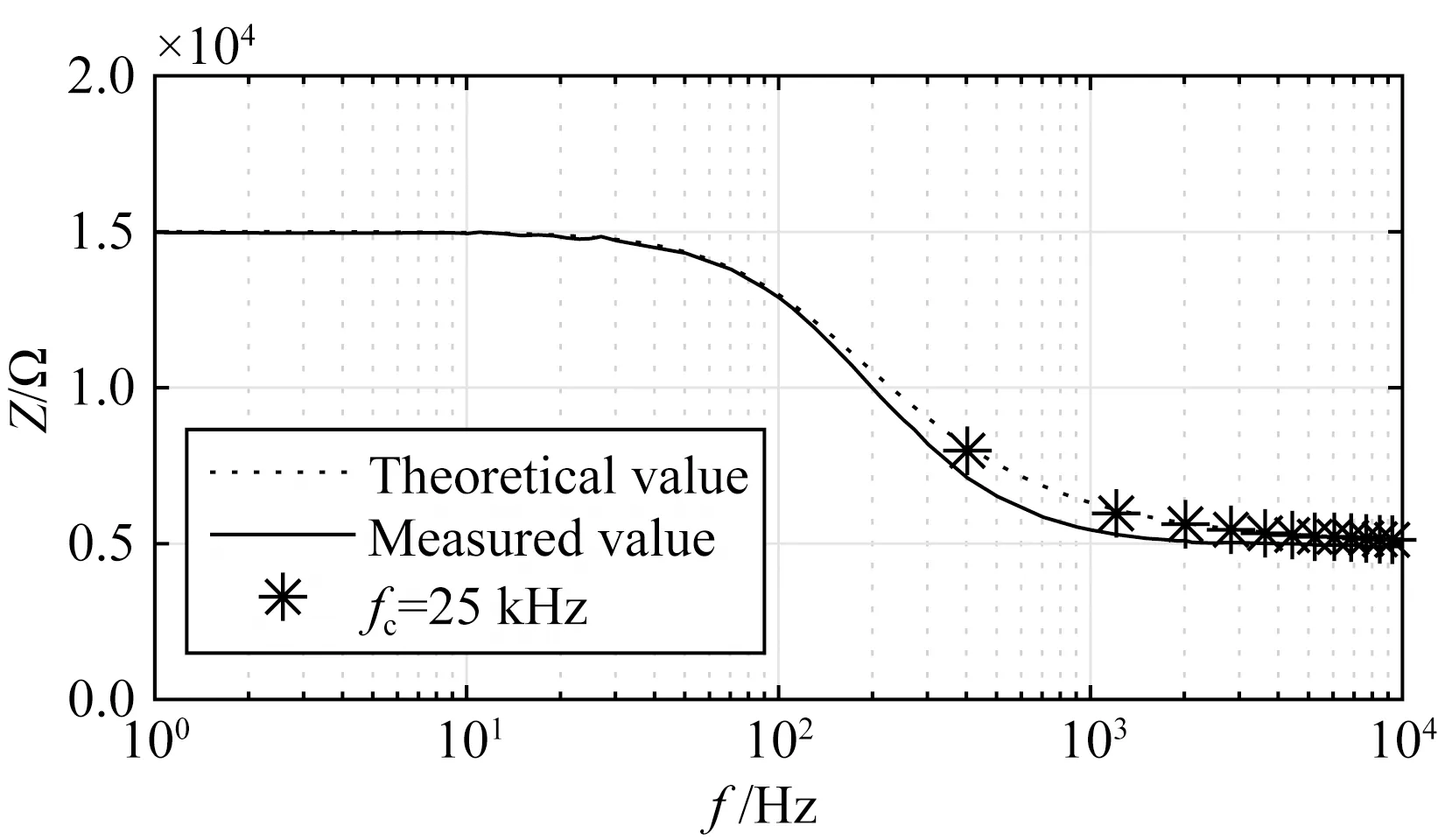
图14 频率响应对比图Fig.14 Comparison of frequency response
发送信号详细参数为I=50 μA,n=5,fc=0.062 Hz、0.62 Hz、6.2 Hz、62 Hz、625 Hz、6.25 kHz、62 kHz.测量频带范围为0.001~11 kHz,按十倍频设置频组,两相邻频组间有重复频段,共包含90个频点如表4所示,实现单次单周期覆盖测量频带用时约18.5 min,采用变频法单次单周期测量以上频点需要耗时约42.6 min,与变频法相比测量效率提高2.3倍.图13展示了转折频率附近频组的波形及其功率谱,图13a—d依次为fc=62 Hz、625 Hz、6.25 kHz、62 kHz的时域响应波形图,图13e—h为对应的功率谱图.
图14为测得频率响应与理论值对比图,从图中可知测得幅频曲线在工频附近无明显变化.频率较大时存在系统误差,按照式(18)的修正方法,计算出系统频率响应并标定后,另取fc=25 kHz的频组重新测量,测得响应呈现于图14中,测量误差如表3所示,标定后的测量误差小于0.5%.
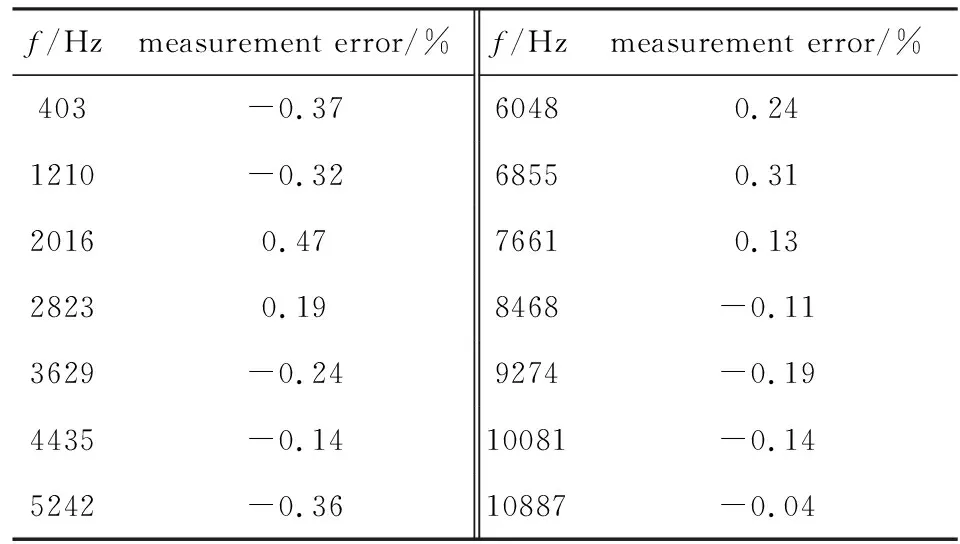
表3 测量误差表Table 3 Measurement errors
5 结论与展望
本文基于逆重复m序列的编码原理,论述了逆重复m信号的功率谱特点,推导了抗工频干扰的参数选择方法.从观测装置角度详细分析了驱动能力及阻抗匹配、测试系统的频率响应、以及高频微弱信号的产生与拾取等关键问题.以5阶序列为例的实验结果表明:
(1)该方法可在10-3~104kHz频带内测量90个有效频点,实现宽频带、多频点的观测目的;同时,可根据需要改变逆重复m信号参数加密频点,获得更高的频率分辨率.
(2)抗工频干扰能力强,通过合理选择信号参数,使发送信号不包含工频分量,可以有效压制工频干扰.
(3)测量精度高,通过系统响应修正公式对系统进行标定后,测量误差小于0.5%.
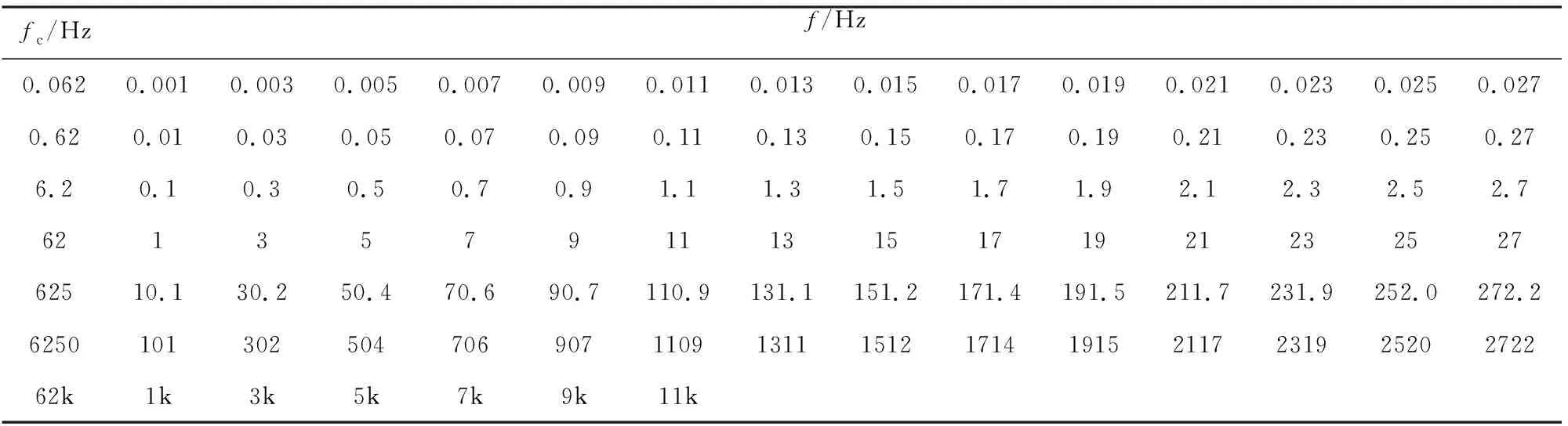
表4 5阶信号在测量频带内包含的频点Table 4 Frequency points of 5th-order signal contained in the measurement frequency band
(4)测量效率高,测量效率由逆重复m序列阶数决定,5阶序列的测量效率相比变频法测量提高2.3倍,在实际观测工作中可根据需要适当提高阶数以获得更高测量效率.
(5)恒流源输出采用分档连续可调方案,在μA 级精度上可实现以1 μA为单位的输出电流调整.
(6)观测数据中有效频点增加,为岩矿石电性参数计算与分析提供了基础数据保证.
通过理论分析与实验结果,可以展望下一步工作重点:
(1)接收系统通过MN拾取大于3 dB有效信号后利用虚拟仪器技术上传至上位机(PC机)对时间波形保存,以便于进行后续计算与分析.
(2)通过时间波形的时频计算,可在一次测量中,分别求取到时间域与频率域电性参数的各类曲线,同时可利用导电模型,得到模型的各二级谱参数,进一步增强观测数据的通用性.
感谢在文章撰写过程,得到中国科学院地质与地球物理研究所底青云研究员的指导,在此表示感谢.

