基于二维图像的数字岩心电导率计算方法研究

包宏帅， 韩同城,2* ， 符力耘,2

1 中国石油大学(华东)地球科学与技术学院， 山东 青岛 266580 2 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室， 山东 青岛 266071

0 引言

电导率是表征岩石电学性质的重要物理参数之一，不仅在探索岩石矿物微观导电机制和研究地球内部物质结构组成等方面作用显著(Glover et al.，1994；Calleja et al.，2001；Nover，2005；蒋建军等，2013；郭颖星等，2018)，还对地质资源勘查和测井解释等领域有着重要的指示作用(Archie，1942；Duba et al.，1978；方胜和罗延钟，1991；李剑浩，1993；Revil et al.，1998).因此，准确、快速地确定岩石的电导率具有巨大的研究和应用价值.

作为近年来发展的一种岩石物理数值模拟工具(朱伟和单蕊，2014；孔强夫等，2015；Saxena and Mavko，2016；Saxena et al.，2017)，数字岩心技术已经成为有效计算岩石电导率等物性参数的重要方法(Arns et al.，2001；孙建孟等，2012；Andrä et al.，2013b；林承焰等，2018).此外，数字岩心技术可以在微观尺度上定量分析孔隙尺寸、湿润性、泥质等因素对岩石电导率的影响(Yue and Tao，2008；Liu et al.，2009；Yue et al.，2011；Miller et al.，2015)，这为系统地研究岩石的导电特性奠定了基础.

一般情况下，数字岩心技术基于三维微观结构生成的三维网格(Arns et al.，2005；Golab et al.，2010；Andrä et al.，2013a)对岩石电导率进行数值计算(Andrä et al.，2013b).许多学者利用数字岩心技术对岩石的导电特性开展了大量研究.Arns等(2001)在早期研究(Fredrich et al.，1993；Schwartz et al.，1994；Spanne et al.，1994；Auzerais et al.，1996)的基础上讨论了有限体积、离散化和统计波动等误差源的影响，通过数字化三维微观结构图像计算了枫丹白露砂岩的电导率特性.Liu等(2009)利用有限元方法计算了三维数字岩心的电阻率和地层因素，研究了岩石湿润性对岩石电学性质的影响.Zhan等(2010)通过X射线CT图像计算了贝雷砂岩的电导率，并建立了考虑表面电导的三相导电模型.Andrä等(2013a，b)系统总结了数字岩心图像处理手段和有效性质计算方法，形成了一套数字岩石物理工作的流程基准.Miller等(2015)通过数字岩心技术对橄榄石-玄武岩熔体电导率进行了估算，讨论了挥发组分和熔体膜对部分熔融岩石电导率的潜在影响.Yue(2019)利用格子气自动机方法研究了岩石的导电性质，并将孔隙复杂度随孔隙度的变化率与岩石胶结系数相联系，进而揭示了岩石胶结系数的各向异性和物理意义.上述研究验证了数字岩心技术计算岩石电导率的可行性和有效性，特别是在考虑微观因素对岩石电导率的影响方面，三维数字岩心技术丰富了我们的研究手段，有助于对岩石的电学性质展开系统的研究.数字岩心技术计算岩石电导率的关键是岩石三维微观结构的获取，但是利用X射线CT扫描等方法直接获取岩石三维微观结构既费时又昂贵(姚军等，2005；Saxena et al.，2017)，这限制了数字岩心技术在一系列地球物理研究中的大规模应用.

相比于三维微观结构，岩石的二维微观结构信息更易获得、更加普遍(朱益华和陶果，2007；Saxena and Mavko，2016).因此，许多学者在岩石二维微观结构信息的基础上，通过重建方法(例如随机法、过程法等)来构建三维数字岩心(Quiblier，1984；Bakke and Øren，1997；Hazlett，1997；Liang et al.，2000；Hidajat et al.，2002；Keehm et al.，2004；朱益华和陶果，2007；刘学锋等，2013；莫修文等，2016)，进而开展对岩石电导率等性质的研究.此外，有学者选择通过岩石二维信息来直接研究二维微观结构与岩石物性之间的联系(Saxena and Mavko，2016；Saxena et al.，2017).Adler等(1992)、Øren和Bakke(2002)利用二维图像微观结构信息成功重建了三维数字岩心，并计算了岩石的电导率和地层因素，在与实验数据对比的基础上验证了通过重建三维数字岩心开展物性研究的可行性.利用岩石二维信息来重建三维数字岩心在理解复杂介质物理性质方面具有重要指导意义，然而重建算法复杂多样，并有着不同的适应性和局限性(刘学锋等，2013；Saxena et al.，2017)，因此重建的三维数字岩心存在着许多问题(例如，孔隙连通性不充分、重构孔形状失真或统计特性与真实岩样不符).另一方面，Saxena和Mavko(2016)直接计算了岩石二维微观结构的弹性特性，并与三维数字岩心的弹性特性进行了关联，在此基础上通过经验变换计算了三维数字岩心的弹性模量和声波速度.Saxena等(2017)用相似的方法研究了二维薄片与岩石的渗透率关系，并通过一个可校准的模型对三维数字岩心的渗透率进行了计算.上述方法不需要通过岩石二维微观结构来重建三维数字岩心，成本低、耗时短，并且有效避免了重建算法的局限性，为准确快速确定岩石的物性提供了思路.此外，在相同的计算机内存条件下，可以从更大的二维视场来估计三维数字岩心的性质，这具有重要的现实意义，但是利用二维微观结构信息估算岩石电导率的研究尚未见到报道.

本文研究了岩石二维与三维数字岩心的电导率联系.我们对2个贝雷砂岩和1个枫丹白露砂岩样品进行了微米级X射线CT扫描，得到了岩石的三维微观结构信息，经图像分割处理等操作后建立了三维数字岩心.通过有限元法计算的三维数字岩心电导率与实验数据的对比，验证了数值计算方法的有效性.随后我们数字地扩展了岩石的孔隙，产生了新的三维数字岩心样本，在此基础上，利用有限元方法计算了三维数字岩心以及相应岩石二维数字岩心的电导率.随后基于二维与三维数字岩心胶结系数之间的联系建立了二维与三维电导率变换关系，并通过与有限元法计算的三维数字岩心电导率的对比验证了基于二维图像的数字岩心电导率计算方法的可行性和有效性.

1 数值计算

1.1 有限元数值计算方法

有限元法是数字岩心技术计算岩石电导率的经典方法(Garboczi，1998；Liu et al.，2009；Yu and Wu，2010；Andrä et al.，2013b；Miller et al.，2015；孔强夫等，2015)，在复杂微分方程近似解的求取方面优势明显(底青云和王妙月，1998).有限元方法的基本思想是“离散逼近”，即在离散的单元中利用一系列的基底函数组合来近似代替求解函数(曾攀，2009).利用有限元方法计算岩石电导率的理论基础是变分原理，我们基于Garboczi(1998)的有限元方法计算了三维数字岩心和相应岩石二维数字岩心的电导率.Andrä等(2013b)将这种有限元法与其他数值计算方法进行了比较，并在各种数值方法之间找到了合理的一致性.

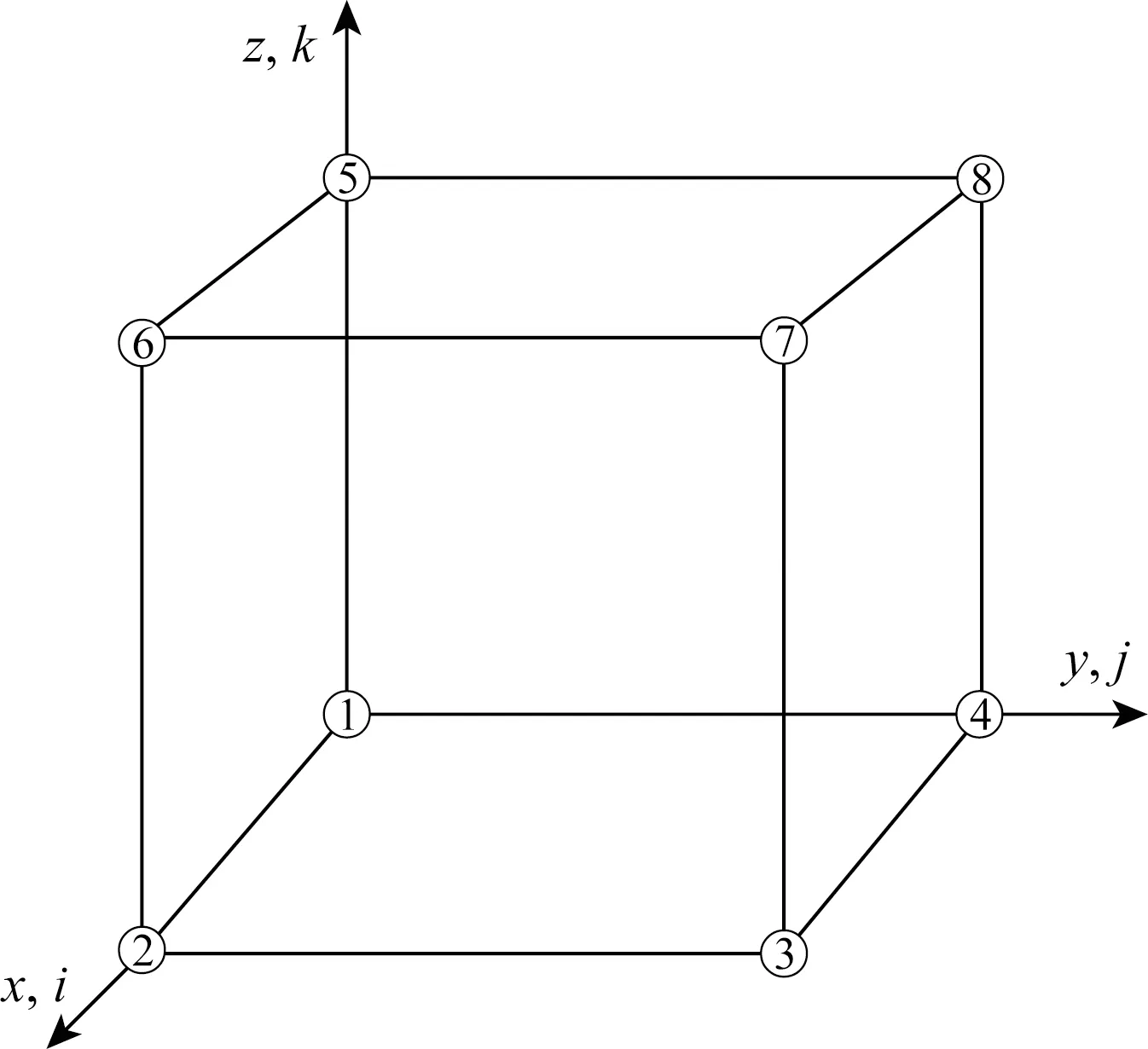
图1 像素(单元)结点编号示意图Fig.1 Diagram of labeled node with one pixel

三维数字岩心的每一个像素可视为一个8结点的立方体单元，像素内的结点编号如图1所示.在三维数字岩心上的任意两端施加电场，每个像素上最终的电压分布确定了三维数字岩心的能量.根据变分原理，求解每个像素上的电压分布问题转化为求解系统能量极小值问题，即需要使得系统能量满足对节点电压的偏导数为零.在数值求解过程中，当系统能量对节点电压的偏导数构成的梯度矢量的平方和小于某一给定允许误差时，可近似认为系统能量取得了极小值，即确定了三维数字岩心的电压分布和有效电导率(Garboczi，1998).

(1)

其中，ur是结点上的电压(r的变化范围为1到8，s与r的变化范围一致)，Drs是通过Simpson公式精确计算的刚度矩阵(Garboczi，1998；曾攀，2009)，大小取决于该像素所代表的岩石组分的电导率张量.为了将单个像素的能量与三维数字岩心的总能量联系起来，需要将像素内的结点编号与整体的结点编号相联系.在三维数字岩心中，非边界上的结点m(i,j,k)被相邻8个像素所共用，即结点m有27个与之相邻的结点，相邻的结点位置可由结点m的坐标加减0或1计算.对于周期性边界条件，相邻结点可能处于三维数字岩心的另一侧.应用周期性边界条件，并考虑由边界条件引起的边界单元上的电压跨度，则给定像素的能量可表示为

(2)

其中，δr是三维数字岩心边界和端点处的结点电压校正值，与施加的外部电场E=(Ex,Ey,Ez)有关.利用总能量取极小值，采用共轭梯度法求解所有结点上的电压值(Garboczi，1998；曾攀，2009)，能量梯度为

(3)

其中，Am n和bm为全局变量，与每个像素的刚度矩阵Drs有关.在确定了结点上电压后，利用三线性插值函数可计算三维数字岩心的平均电流和总能量等参数.最后，通过电场和计算的体积平均电流密度，应用欧姆定律可得到岩石的等效电导率：

〈jp〉=〈σp qeq〉=σpEp，

(4)

其中，〈jp〉表示p方向(下标p分别为x、y、z方向，q与p表示的含义一致)的体积平均电流密度，eq为像素的内部电场(定义为像素内部电压的偏微分，内部电压可由8个结点的电压线性插值确定)分量，σp q为像素的电导率张量，取决于该像素所代表的岩石组分，σp表示p方向的等效电导率.

1.2 有限元法有效性验证

为了验证Garboczi(1998)有限元方法计算岩石电导率的有效性，我们首先选取了两个不同孔隙度的贝雷砂岩(分别记作贝雷砂岩1和贝雷砂岩2)和一个枫丹白露砂岩样品进行实验室电导率测量，然后利用有限元方法计算了三个样品的三维数字岩心电导率，最后对有限元法计算的三维数字岩心电导率与实验室测量的电导率数据进行了对比.

由于X射线CT扫描的分辨率有限，因此无法识别岩石中存在的所有微孔隙.为了能够通过对比验证有限元法计算三维数字岩心电导率的有效性，我们对岩石样品施加围压以期关闭岩石中无法被识别的微孔隙，降低微孔隙对岩石导电性质的影响.实验前，将三个砂岩样品置于温度为70 ℃的干燥箱中干燥24 h，得到完全干燥的岩石样品.随后，在含有矿化度为80 g·L-1的氯化钠溶液(实验室测定电导率为11.3 S·m-1)的真空容器中持续抽真空12 h，并在16 MPa的压力下对岩石样品加压饱和12 h，以确保岩石样品完全饱和.然后，分别在5、10、15、20、30、40、50和60 MPa的围压条件下，通过型号为TH2822A电阻测量仪测量了岩石样品的电阻，测量频率为1 kHz.每次改变压力时，将样品静置10 min，使岩石骨架与孔隙流体之间达到稳定状态，确保岩石样品电阻测量结果的准确性.在得到不同压力下的岩石样品电阻R后，岩石的电导率可由公式(5)计算得到：

(5)

其中，L和S分别是砂岩样品的实测长度和横截面积.

岩石电阻测量完成后，分别在与电阻测试相同的围压条件下，通过CMS300覆压孔隙度渗透率测量系统测量了砂岩样品的孔隙度，其中贝雷砂岩1、贝雷砂岩2和枫丹白露砂岩在5 MPa压力下的孔隙度分别为20.06%、14.59%和8.87%.贝雷砂岩1和贝雷砂岩2在5 MPa压力下的渗透率分别约为288.304 mD和22.001 mD.随后，我们对实验所用的岩石样品进行切割取样，分别在贝雷砂岩1和贝雷砂岩2上钻取了直径约为4 mm的小型柱状岩样，在枫丹白露砂岩样品上钻取了直径约4.5 mm的小型岩样.通过微米级X射线CT技术分别对三个小型岩样进行扫描，获得了其岩心横截面的一系列微观结构信息，扫描图像的像素分辨率均为1.7 μm.在分辨率一定的情况下，三维数字岩心包含的像素越多，越能准确反映岩石的微观结构，并且岩石物理数值模拟的结果可靠性越强，但考虑到计算机存储和运算能力的限制，需要对三维数字岩心的尺寸大小进行权衡.参考Andrä等(2013a)对岩心CT扫描图像的处理步骤，我们通过Avizo软件进行分水岭分割等操作将灰度图像转变为具有颗粒和孔隙体素的二值化数字样本(如图2所示)，其中贝雷砂岩1和贝雷砂岩2数字样本的大小为600×600×600像素，枫丹白露砂岩数字样本的大小为700×700×700像素，体素边缘长度均为1.7 μm，孔隙显示为黑色，矿物为灰色.贝雷砂岩1、贝雷砂岩2和枫丹白露砂岩的三维数字岩心孔隙度分别为20.02%、14.38%和8.52%，良好的阈值划分使其孔隙度均在5～10 MPa压力下的实测岩石孔隙度范围内，与岩石孔隙的相关统计特性相吻合.图3显示了从三维数字岩心的xz剖面中计算的岩石二维图像(二维数字岩心)的孔隙度分布，每个二维图像可视为在y方向具有一个像素厚度的三维数字岩心，其孔隙度分布较为广泛.为了计算结果的一致性和可对比性，我们选取与实验室测量相同的z方向进行三维数字岩心的电导率数值计算，用石英作为岩石骨架中的矿物，电导率设为1×10-5S·m-1，孔隙流体电导率为11.3 S·m-1.

病株主要特点：病株矮小、生长速度慢、并且叶片失水较重呈灰绿色，随后叶片由下向上黄化，茎部会因为病菌侵袭发生水渍状腐烂。最后使苗株死亡，造成苗株缺失断垄，严重些会导致整亩没有植株存活。

图2 数字岩心样本(a) 贝雷砂岩1，600×600×600像素； (b) 贝雷砂岩2，600×600×600像素； (c) 枫丹白露砂岩，700×700×700像素.孔隙显示为黑色，矿物为灰色.体素边缘长度均为1.7 μm.Fig.2 Binary digital rocks(a) Berea sandstone sample 1 of size 600×600×600; (b) Berea sandstone sample 2 of size 600×600×600; (c) Fontainebleau sandstone sample of size 700×700×700. Pores are shown in black and mineral in grey. Voxel edge length for all sandstone samples is 1.7 μm.

图3 岩石二维图像(数字岩心)的孔隙度分布直方图(a) 贝雷砂岩1； (b) 贝雷砂岩2； (c) 枫丹白露砂岩.平均孔隙度用黑色五角符号表示.Fig.3 Histograms of porosity estimated from 2D images (digital rocks) for rock samples(a) Berea sandstone sample 1; (b) Berea sandstone sample 2; (c) Fontainebleau sandstone sample. Average porosity from 2D images is shown with the black pentagon symbol.

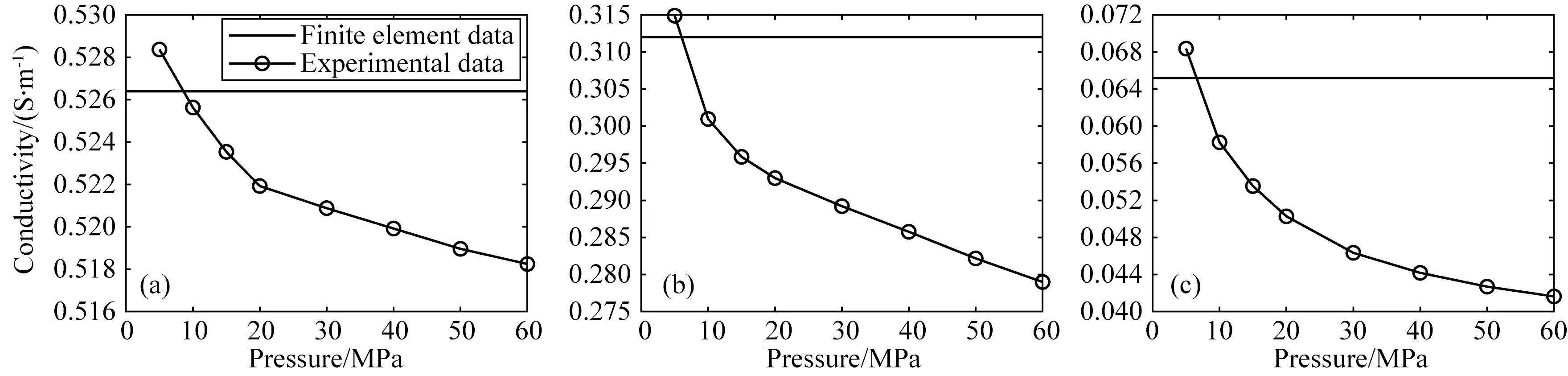
图4 实验测量与有限元法计算的电导率对比(a) 贝雷砂岩1； (b) 贝雷砂岩2； (c) 枫丹白露砂岩.三维数字岩心的电导率显示为黑色直线.Fig.4 Comparison of electrical conductivity between experimental measurement and finite element method(a) Berea sandstone sample 1; (b) Berea sandstone sample 2; (c) Fontainebleau sandstone sample. The electrical conductivity data point of 3D digital rock is displayed as black straight line.

三维数字岩心的电导率与岩石样品的实测值之间存在着差异，除实验操作和仪器误差外，主要受两方面客观因素的影响.一方面，由于岩心CT扫描图像的分辨率有限，因此岩石样品的所有微孔隙不能完全被识别，使得三维数字岩心的孔隙度和导电路径与实际样品存在偏差，进而造成了电导率之间的差异.另一方面，岩石样品存在着非均质性，尺寸大小有限的三维数字岩心无法完全代表岩石的整体孔隙结构和物理特性，因此也会导致三维数字岩心与岩石样品之间的电导率存在着差异.图4显示了有限元法计算的三维数字岩心电导率与不同压力下电导率测量值的对比，为便于比较，三维数字岩心电导率数据点显示为黑色直线.随着压力的增加，砂岩样品中的许多微孔隙被关闭，有效的导电路径随之减少，使得岩石的电导率降低. 岩心CT扫描图像经阈值分割处理后使得三维数字岩心的孔隙度均在5～10 MPa压力下的实测岩石孔隙度范围内，而有限元法计算的三维数字岩心电导率也在5～10 MPa压力下的实测电导率范围内，三维数字岩心相应的孔隙度和电导率均与实测结果有良好的对应，这不仅验证了Garboczi(1998)有限元方法的有效性，还侧面反映了对岩心CT扫描图像的良好分割处理，为利用有限元法计算三维数字岩心的电导率奠定了基础.

1.3 二维和三维数字岩心电导率计算

在本文中，我们基于Garboczi(1998)的有限元方法对三维和二维数字岩心的电导率进行计算，其方法原理和有效性验证已进行了阐释.为了建立岩石三维和二维数字岩心之间的电导率联系，我们需要对相应数字岩心的电导率和孔隙度进行关联，即通过不同孔隙度的三维和二维数字岩心来进行电导率的有限元计算.我们将图2a所示的样本记为贝雷砂岩1的数字样本A(如图5a所示)，假设贝雷砂岩1的岩石骨架矿物全为石英，并且颗粒表面生长均匀，通过Avizo软件相关模块数字地缩小原始贝雷砂岩1样本A的颗粒，产生了另外两个数字岩石样本B和C(如图5b、5c所示).同样地，我们分别对贝雷砂岩2和枫丹白露砂岩的原始数字样本进行相关操作，得到了孔隙度较大的两个数字样本B和C，贝雷砂岩2和枫丹白露砂岩的三个三维数字岩心样本分别如图6和图7所示.表1给出了各岩石的三维数字样本的孔隙度信息.另外，本文提到的岩石二维数字岩心是从图5、6、7所示的相应三维数字岩心样本的xz剖面得到的，可视为在y方向具有一个像素厚度的三维数字岩心，从原始三维数字样本(即各岩石的样本A)中得到的岩石二维数字岩心的孔隙度分布已由图3给出.最后，我们选取与实验室测量相同的z方向对上述二维与三维数字岩心进行电导率计算模拟，以保证计算结果的一致性和可对比性.

表1 三维数字砂岩样本的孔隙度信息Table 1 Porosity information of 3D digital sandstone samples

图5 贝雷砂岩1的三个数字样本(a) 图2a显示的原始贝雷砂岩1，记为贝雷砂岩1的“样本A”，孔隙度为20.02%； (b) 数字地缩小贝雷砂岩1的“样本A”的颗粒形成的贝雷砂岩1“样本B”，孔隙度为22.21%；(c)数字地缩小贝雷砂岩1的“样本A”的颗粒形成的贝雷砂岩1“样本C”，孔隙度为24.40%.Fig.5 Three digital samples of Berea sandstone 1(a) Original image of Berea sandstone sample 1 shown in Fig.2a is referred as Berea sandstone 1 “sample A”, with porosity of 20.02%; (b)Berea sandstone 1“sample B” is derived by reducing numerically the grains in Berea sandstone 1 “sample A” , with porosity of 22.21%; (c) Berea sandstone 1 “sample C” is derived by reducing numerically the grains in Berea sandstone 1 “sample A” , with porosity of 24.40%.

图6 贝雷砂岩2的三个数字样本(a) 图2b显示的原始贝雷砂岩2，记为贝雷砂岩2的“样本A”，孔隙度为14.38%； (b) 数字地缩小贝雷砂岩2的“样本A”的颗粒形成的贝雷砂岩2“样本B”，孔隙度为16.34%； (c) 数字地缩小贝雷砂岩2的“样本A”的颗粒形成的贝雷砂岩2“样本C”，孔隙度为18.36%.Fig.6 Three digital samples of Berea sandstone 2(a) Original image of Berea sandstone sample 2 shown in Fig. 2b is referred as Berea sandstone 2 “sample A”, with porosity of 14.38%; (b) Berea sandstone 2 “sample B” is derived by reducing numerically the grains in Berea sandstone 2 “sample A” , with porosity of 16.34%; (c) Berea sandstone 2 “sample C” is derived by reducing numerically the grains in Berea sandstone 2 “sample A” , with porosity of 18.36%.

图7 枫丹白露砂岩的三个数字样本(a) 图2c显示的原始枫丹白露砂岩，记为枫丹白露砂岩的“样本A”，孔隙度为8.52%； (b) 数字地缩小枫丹白露砂岩的“样本A”的颗粒形成的枫丹白露砂岩“样本B”，孔隙度为10.47%； (c) 数字地缩小枫丹白露砂岩的“样本A”的颗粒形成的枫丹白露砂岩“样本C”，孔隙度为12.42%.Fig.7 Three digital samples of Fontainebleau sandstone(a) Original image of Fontainebleau sandstone sample shown in Fig.2c is referred as Fontainebleau sandstone “sample A”, with porosity of 8.52%; (b) Fontainebleau sandstone “sample B” is derived by reducing numerically the grains in Fontainebleau sandstone “sample A” , with porosity of 10.47%; (c) Fontainebleau sandstone “sample C” is derived by reducing numerically the grains in Fontainebleau sandstone “sample A” , with porosity of 12.42%.

2 基于二维图像计算三维数字岩心电导率

2.1 基于二维图像的三维电导率计算方法

岩石的等效电导率与岩石骨架矿物和孔隙填充流体的电导率有关.在大多数沉积岩中，固体颗粒的电导率通常比孔隙流体的电导率低一个或几个数量级，在这种情况下，等效电导率由流体性质及含量、样品孔隙度和孔隙空间连通性等因素决定.Archie(1942)给出了常用于表征岩石电导率和孔隙度关系的公式：

(6)

其中，σw是岩石孔隙中流体的电导率，σ0是完全饱和该流体时的岩石电导率，φ是孔隙度分数，m是胶结系数.

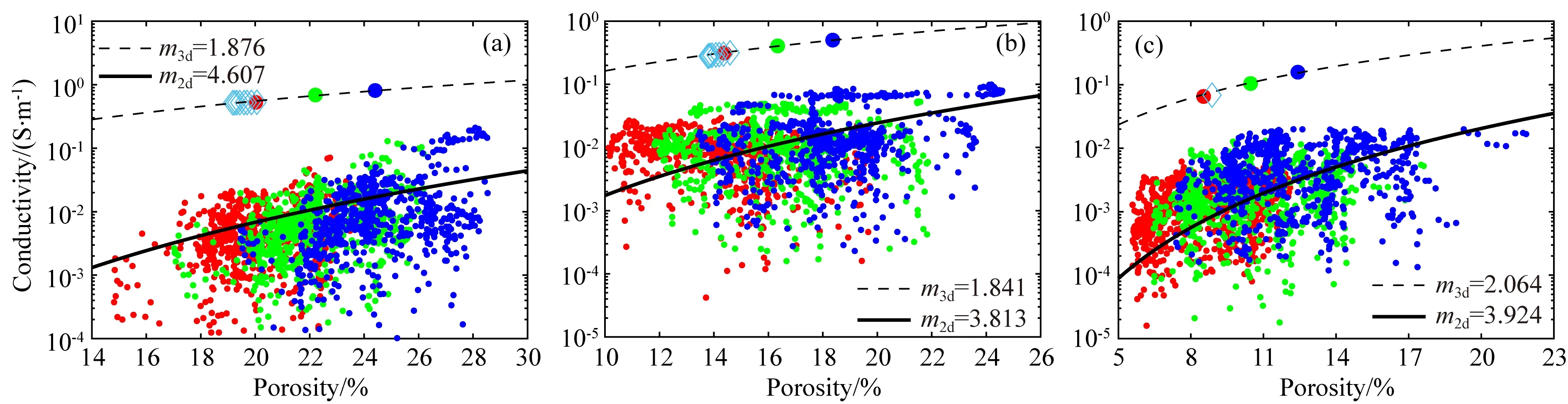
图8 岩石数字样本的电导率与孔隙度关系(a) 贝雷砂岩1； (b) 贝雷砂岩2； (c) 枫丹白露砂岩.计算结果显示了三块岩石的三维数字样本(大圆点符号，红色、绿色、蓝色分别表示各岩石的样本A、B、C，与图5、6、7中所示的三维数字岩心样本相对应)以及相应的二维数字岩心(小圆点符号，红色、绿色、蓝色分别表示各岩石的样本A、B、C的二维数字岩心)的电导率.虚线与实线分别代表通过Archie公式拟合得到的三维数字样品以及相应的二维数字岩心电导率-孔隙度关系，m3d和m2d分别为其胶结系数.实验室测量的岩石电导率如菱形符号所示.Fig.8 The electrical conductivity versus porosity for different rock samples(a) Berea sandstone sample 1; (b) Berea sandstone sample 2; (c) Fontainebleau sandstone sample. Calculations are shown for the 3D digital samples of three rocks (large dot symbols; red, green and blue represent samples A, B and C of each rock, respectively, corresponding to the 3D digital rock samples shown in Fig.5, 6, and 7) and the corresponding 2D rocks (smaller dot symbols; red, green and blue represent 2D rocks of samples A, B and C of each rock, respectively). The dashed curve and solid curve represent the conductivity-porosity trend (fitted by Archie equation) of 3D digital samples and the corresponding 2D digital rocks respectively, m3d and m2d are the cementation coefficients. Laboratory data points of rock conductivity are shown in diamond symbol.

图8显示了有限元方法计算的三维数字岩心(图中的大圆点)以及相应岩石二维数字岩心(图中的小圆点)的电导率与孔隙度之间的关系，红色、绿色、蓝色分别代表图5、6、7中所示的各砂岩的样本A、B、C.结果表明，三维数字岩心的电导率随着孔隙度的增大而增大，与实验室得到的电导率随孔隙度的变化趋势(如图8中的菱形符号所示)相吻合.另外，由于二维数字岩心之间的孔隙度、孔隙分布以及孔隙连通性存在差异，使得图8中相应岩石二维数字岩心整体的电导率计算结果约在两个数量级范围内分布，并且在局部可能出现随着孔隙度增加而电导率增幅不明显的现象，但综合图8中所有的小圆点符号来看，总体上呈现二维数字岩心的电导率随孔隙度增加而增大的趋势.相比岩石单个的二维数字岩心，三维数字岩心的孔隙连通性更好、导电路径更多，使得三维数字岩心的电导率更大.此外，我们利用Archie公式分别对三维数字岩心和二维数字岩心的电导率-孔隙度关系进行拟合，确定了相关胶结系数，其拟合结果如图8中的虚线和实线所示，三维数字岩心的胶结系数小于二维数字岩心的胶结系数.拟合的三维数字岩心电导率-孔隙度关系和岩石二维数字岩心电导率-孔隙度关系可由下式表示：

(7)

(8)

其中，σ3d和σ2d分别是拟合的三维数字岩心电导率和岩石二维数字岩心电导率，σw是孔隙中流体的电导率，m3d和m2d分别是三维和二维数字岩心的胶结系数.通过对三个岩石样品的三维与二维数字岩心的胶结系数进行分析计算，我们发现二者之间存在着数量关系，即存在系数M=m3d/m2d.

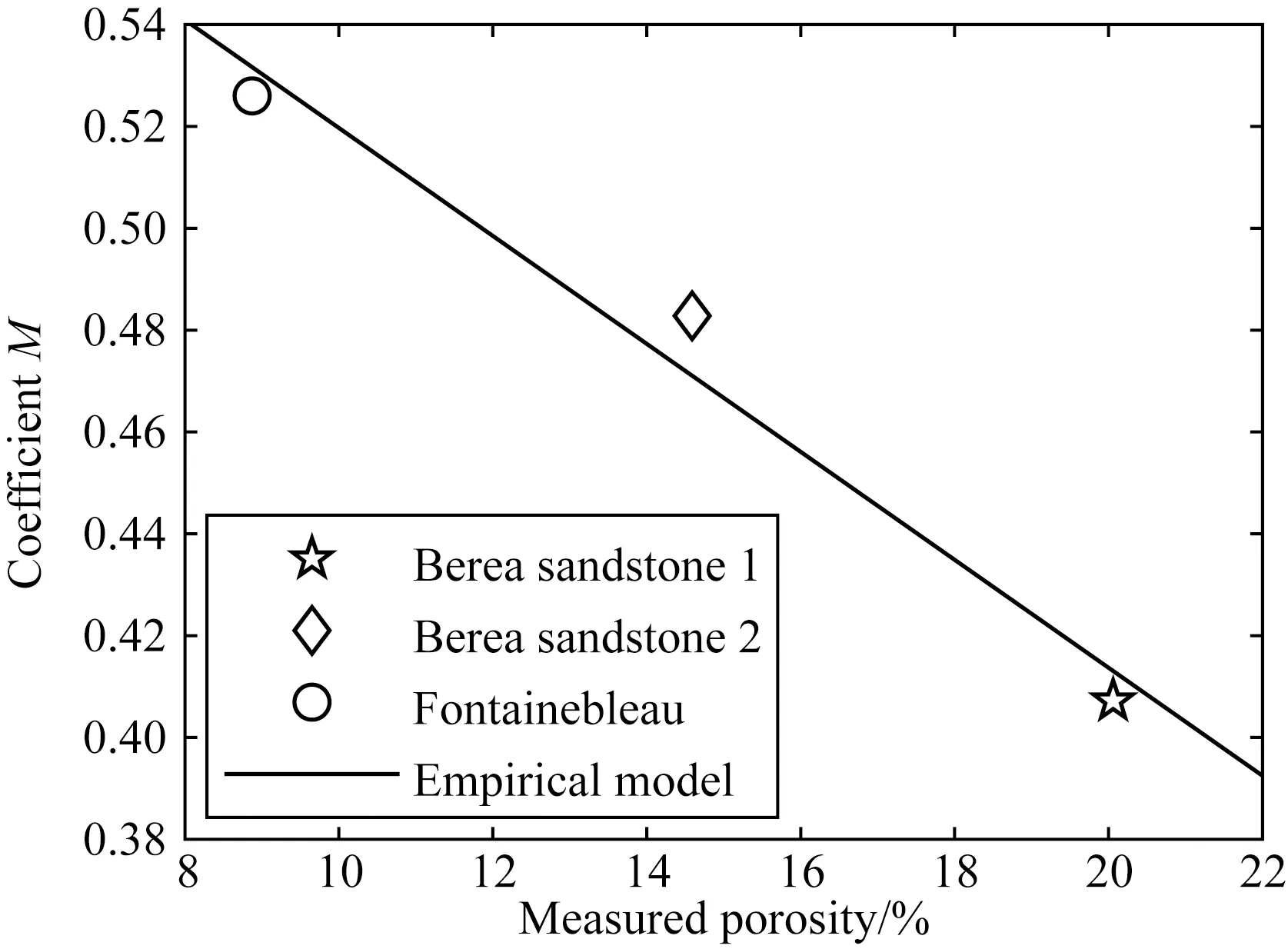
图9 三块岩石的系数M与5 MPa压力下的实测孔隙度的关系.经验模型的解为孔隙度的函数，相关系数R2=0.9717Fig.9 Coefficient M of three rocks (as shown in the legend) versus measured porosity under 5 MPa pressure. Solution of the empirical model is shown as a function of porosity, and the correlation coefficient R2=0.9717

系数M是三维和二维数字岩心的胶结系数的比值，有许多因素可以影响系数M的大小，如孔隙结构形状、泥质含量、孔隙流体矿化度等.对所有可能影响系数M变化的参数进行详尽研究超出了本文的范围.孔隙度是岩石孔隙结构的一种表象，也是表征岩石孔隙的重要参数之一，并且与胶结系数有良好的正相关性.因此，我们研究了岩石孔隙度对系数M的影响.为了实现这一目的，我们根据图8显示的三维与二维数字岩心的胶结系数对M进行了计算，并对M的结果与5 MPa压力下各岩石的实测孔隙度φ进行了拟合(相关系数R2为0.9717)，其结果如图9所示，拟合模型为

M=-1.06φ+0.6257.

(9)

我们发现，在本文岩石样品所涉及的孔隙度范围内，系数M随着孔隙度的增加而线性减小，并且该孔隙度范围已涵盖了使得Archie公式成立的大部分常规储层岩石的孔隙度，其应用性可以得到保证.结合公式(7)、(8)和(9)，利用M的经验模型以及拟合的二维数字岩心电导率-孔隙度关系进行变换，可得到三维数字岩心的电导率-孔隙度关系，变换过程为

(10)

基于二维图像快速计算得到的电导率与孔隙度关系，通过公式(10)可得到三维数字岩心的电导率-孔隙度关系，并进一步利用三维数字岩心的孔隙度计算其电导率.

2.2 方法验证

为了验证基于二维图像的数字岩心电导率计算方法的有效性，我们利用从Yang等(2015)处得到的人工砂岩样品的三维数字岩心进行了相关数值模拟.该三维数字岩心的大小为120×110×100像素，体素边缘长度为5.92 μm，其孔隙度为17.49%.假设其岩石骨架矿物为石英，我们数字地拓展了其孔隙大小，分别得到了孔隙度约为18.45%、19.31%、20.24%和21.59%的三维数字岩心样本，并参考第1节内容通过有限元法对其二维和三维电导率进行了计算，确定了二维数字岩心的胶结系数.利用M的经验模型以及拟合的二维数字岩心电导率-孔隙度关系对三维数字岩心电导率-孔隙度关系进行了预测，其结果如图10a中的黑色点线所示.为了更加清晰地显示图10a中基于二维图像的数字岩心电导率计算方法得到的电导率结果，我们将有限元方法计算的三维数字岩心电导率与其进行了比较，其结果如图10b所示，相关系数R2为0.9689.基于二维图像的数字岩心电导率计算方法得到的电导率结果与有限元方法计算的三维数字岩心电导率有良好的一致性，验证了该计算方法的有效性.本文研究得到的基于二维图像的数字岩心电导率计算方法为快速确定岩石电导率提供了思路，将在研究较大尺寸的三维数字岩心的电导率方面发挥巨大作用，同时为进一步准确地揭示岩石二维与三维数字岩心的物性联系奠定了基础.

图10 (a) 通过公式(10)预测的三维数字岩心电导率-孔隙度关系； (b) 从预测的三维数字岩心电导率-孔隙度关系中得到的三维数字岩心电导率与有限元法计算的三维数字岩心电导率的比较，相关系数R2=0.9689.三维数字岩心的电导率-孔隙度关系是利用M的经验模型以及二维数字岩心电导率-孔隙度关系变换得到的，预测结果显示为黑色点线Fig.10 (a) The conductivity-porosity trend of 3D digital rock samples predicted by equation (10); (b) The electrical conductivity of 3D digital rock samples obtained from predicted conductivity-porosity trend of 3D digital rock samples versus calculated by finite element method, and the correlation coefficient R2=0.9689. The conductivity-porosity trend of 3D digital rock sample is obtained by using the empirical model of coefficient M and the conductivity-porosity trend of two-dimensional digital rocks, and the transformation result is shown in dotted black curves

3 结论

为了合理快速地计算岩石电导率，我们通过微米级X射线CT扫描得到的岩石微观信息建立了三维数字岩心，然后利用有限元法计算了三维数字岩心以及相应岩石二维数字岩心的电导率，并基于电导率与孔隙度的关系对岩石二维与三维数字岩心的电导率联系进行了研究.我们得到以下结论：

(1)基于Archie公式拟合的电导率-孔隙度关系可知，岩石三维数字岩心的胶结系数小于二维数字岩心的胶结系数，并且在本文涉及的孔隙度范围内，二者之间的比值随着岩石实测孔隙度的增加而线性减小.

(2)以岩石三维和二维数字岩心两者胶结系数间的联系为纽带，可利用快速计算得到的二维数字岩心电导率-孔隙度关系进行变换，得到三维数字岩心的电导率-孔隙度关系，进而通过三维数字岩心的孔隙度计算其电导率，并且基于二维图像的数字岩心电导率计算方法得到的电导率结果与有限元法计算的三维数字岩心电导率有良好的一致性.