基于深度学习的接收函数自动挑选方法
李志强, 田有,2,3* , 赵鹏飞,2, 刘财,2, 李洪丽,2
1 吉林大学地球探测科学与技术学院, 长春 130026 2 吉林大学地球信息探测仪器教育部重点实验室, 长春 130026 3 长白山火山综合地球物理教育部野外科学观测研究站, 长春 130026
0 引言
海量地震数据的取得为人类认识地球带来了可能.随着计算机硬件水平的快速提高,应用计算机自动处理地震数据,替代繁复机械的人工流程进行诸如震相识别、走时初至拾取、接收函数挑选、余震序列识别等工作是十分必要的.传统的自动处理算法包括:利用短长时平均比值的STA/LTA方法(Allen, 1978; Withers et al., 1998)进行震相识别,利用“V”字分形曲线首个突变点拾取震相的分形分维法(Sleeman and Van Eck, 1999;赵大鹏等, 2013),利用不同波震相信噪比挑选接收函数等(Gao and Liu, 2014).然而这些方法在处理精度和效率上各有局限,仍需发展更加全面快捷的计算机自动处理方案.
自Hinton等(2006)的开创性工作以来,深度学习蓬勃发展,并在地震大数据的自动处理和油气藏研究中崭露头角.付超等(2018)将卷积神经网络与支持向量机方法结合,提出了多波地震油气储层分布预测的深度学习方法;林年添等(2018)利用卷积神经网络预测地震油气储层;赵明等(2019a,b)利用U型卷积神经网络进行Pg和Sg震相的识别和到时提取,常规的U网络用来处理二维或者三维数据,将其降维设计即可用来处理一维地震波形;蒋一然和宁杰远(2019)利用支持向量机设计了地震信号探测器SSD和震相分离器SPS用来震相的分类和到时的拾取;李健等(2020)利用美国南加州地震台网的200万条震相和噪声数据训练的卷积神经网络模型应用到实际地震数据的震相拾取当中取得了较好的效果;地震紧急预警中的应用可见胡安冬和张海明(2020)的文章;奚先和黄江清(2020)应用卷积神经网络进行地震剖面中散射体的定位和成像.许多优秀的模型和程序包也被分享到开源社区当中供研究人员学习和使用,如用于识别震相的PhasePApy (Chen and Holland, 2016);泛化能力较强的ConvNet (Ross et al., 2018);断层自动识别软件FaultSeg3D (Wu et al., 2018);用以地震走时初至拾取的PickNet等(Wang et al., 2019; Geng and Wang, 2020).
深度学习在地震震相识别、走时拾取、断层识别等领域的发展和应用较快并取得了较好的成果,但是在接收函数研究中仍少有应用.接收函数和地震波一样都是一种时间序列,常规处理中同样需要人工重复机械的挑选.将应用于地震波中的深度学习方法迁移到接收函数挑选是可行且必要的.接收函数在特定的区域具有较为一致的形态,通常会根据P波、Ps转换波以及PpSs+PsPs的震相是否清晰一致选择保留或舍弃,这实质上构成了一种二分类问题,且特征数量较少,使得接收函数的挑选训练不需要巨量的数据,也不需要过于复杂的网络即可达到令人满意的准确度.这一前提保证了即使是流动台站或其他观测周期较短的台站,也可以通过手动挑选少量接收函数来构建训练集,使用训练后的模型对剩余数据以及小于5.5级的小震数据进行挑选,以实现节省人工、提高整体接收函数质量的目的.而对于永久台站,训练一次模型就可以供以后本台所有数据的挑选使用,若能建立起区域台网模型字典,将具有较高的应用价值.
卷积神经网络(Convolutional Neural Network, CNN)是深度学习中具有代表性的一种,其人工神经元可以使邻近的神经元之间互相产生影响.常规的卷积神经网络包括卷积层(Convolutional Neural Layers)、池化层(Max Pooling)和全连接层(Fully Connected Neural Layers,FCN).相比其他深度学习结构,CNN在图像识别和语音识别方面具有一定优势,且已经有很成熟的开源框架,可以较容易的搭建出面向接收函数挑选问题的网络结构.据此本文设计了一种CNN网络来挑选接收函数,并采用实际观测数据来验证方法的可行性.
1 数据和方法
1.1 接收函数提取
本文所使用的数据取自中国地震局的两台永久台站,黑龙江省牡丹江地震台(MDJ)和北京地震台(BJT).两个地震台都具有较长的地震观测周期,能够提取大量接收函数应用模型训练.两个台站使用的数据下载自美国地震学研究联合会(Incorporated Research Institutions for Seismology, IRIS)网站(http:∥ds.iris.edu),选取2000年到2019年的震级大于5.1级、震中距30°~ 90°的三分量事件波形数据.根据P波理论到时截取波形P波前20 s,后60 s.之后进行去均值、尖刺、倾斜操作,并对数据进行0.05~10 Hz的带通滤波,并由ZNE(垂、北、西)坐标系旋转至ZRT(垂、径向、切向)坐标系.采用时间域迭代反褶积方法(Ligorria and Ammon, 1999)计算接收函数,高斯因子设置为2.5.
对得到的MDJ台15329条接收函数、BJT台14524条接收函数进行人工挑选和标签的制作.接收函数保存为sac文件格式,截取P波前5 s,后25 s共30 s的数据,采样率20 Hz,保留的接收函数头文件中t1参数设置为1,舍弃的t1参数设置为0.
1.2 神经网络搭建
本研究搭建的神经网络基于LeNet-5(LeCun et al., 1998, 2015)手写数字识别模型.如图1所示,整个网络有7层,前4层为卷积层和池化层交替,输入为一维序列,对其进行卷积,使用大小为1×5的一维卷积核,滑动步长1,深度16,选用ReLU函数作为激活函数,此时神经元数量为600×16=9600个.后接一层池化层,设定一个1×2的滑动窗口,滑动步长为2,选取其中的最大值输出到下一层,神经元数量减少到4800个.重复进行一次卷积、池化操作,神经元数目进一步减少到2400个.后3层为全连接层,大小设置为256、60和2,采用Dropout(Srivastava et al., 2014)方法,按照0.5的概率舍弃部分神经元以防止训练过程中的过拟合情况发生.
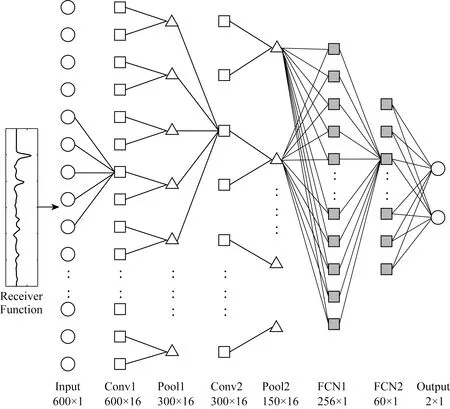
图1 深度学习自动挑选接收函数网络结构每个几何图形代表网络中的一个节点. 网络下方列出了每一层的类型以及对应的节点数、通道数.Fig.1 Architecture of the deep learning network used for receiver functions auto-pickingEach shape corresponds to a node in the net. The characteristics of each layer, number of nodes and channels are also listed at the bottom.
对于接收函数挑选,只有两种结果:保留、舍弃.这本质上构成了一种二分类问题,我们可以对输出结果进行One-hot编码,保留编码为[1,0],舍弃编码为[0,1].基于TensorFlow(ver:1.15.0, https: ∥www.tensorflow.org)软件平台和Python(ver:3.7.3)语言环境搭建深度学习模型,每次输入100个带标签的接收函数作为一个训练批次,采用加入L2正则化的交叉熵损失函数作为Loss函数,利用Adam优化算法(Kingma and Ba, 2014)训练网络参数,最大训练次数设置为30000次.训练采用一块NVIDIA Quadro P5200显卡,训练耗时140 s左右.
1.3 网络训练
接收函数形态受地形影响较大,不同的地壳结构获得的接收函数具有一定的差异.例如高原地区的接收函数由于地壳过于复杂,各个震相会难以辨别(Shi et al., 2015),而沉积盆地地区的接收函数直达P波、转换波和多次反射波会被沉积层混响所覆盖(朱洪翔等, 2018).因此采用单台计算出的接收函数,每台训练一个属于自己的模型,将在一定程度上保证训练和测试样本的相关性,从而降低学习难度,提高识别准确率.
首先要构建训练集和测试集,我们将两个台站的所有数据进行人工挑选,并按照上文所述对t1参数进行标记.训练集使用2000年到2016年的数据,测试集使用2017年到2019年的数据.MDJ训练集13531个接收函数中带有保留标签的有1969个,占比14.5%;测试集1798个接收函数中带有保留标签的有283个,占比15.7%;BJT训练集12730个接收函数中带有保留标签的有3285个,占比25.8%;测试集1812个接收函数中带有保留标签的有496个,占比27.3%.
两个台站的网络结构从8000次训练左右开始收敛稳定,如图2所示的Loss变化曲线.二分类问题常用的评价标准包括准确率和召回率,准确率表示正负样本被正确分类的比例,召回率表示在实际为正的样本中被预测为正样本的比例,二者计算公式如公式(1)、(2)所示:
(1)

(2)
其中ACC表示准确率,TPR表示召回率,NTP表示正类样本被正确分类的数目,NTN表示负类样本被正确分类的数目,NFP表示负类样本被分为正类的数目,NFN表示正类样本被分为负类的数目.
使用最终训练模型测试两个台站的测试集,MDJ台的准确率达到92.3%,召回率达到71.0%,BJT台的准确率达到93.1%,召回率达到84.8%.两台测试集的挑选情况以混淆矩阵热力图的形式在图3给出.MDJ台召回率较BJT台低,经分析是MDJ台测试集正类样本所占比例较低所致.两台站原始接收函数见图4(a、e),自动挑选结果见图4(b、f),人工挑选结果见图4(c、g),可以看出自动挑选结果与人工挑选结果具有较高的相似性.由于标签的制作具有比较大的主观因素,因此存在将质量稍差
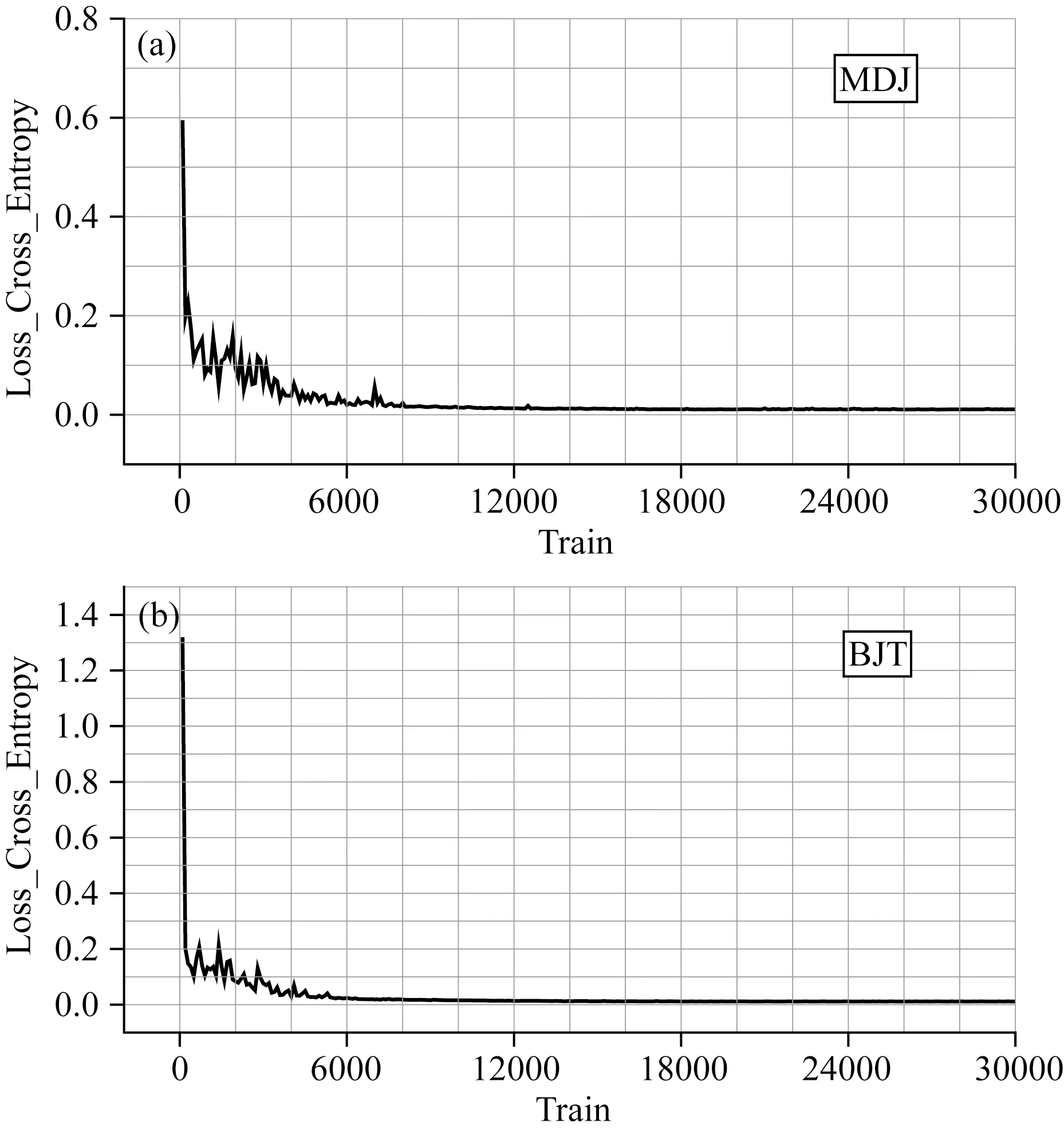
图2 Loss函数随训练次数变化曲线(a) MDJ台; (b) BJT台.Fig.2 Variation curve of loss function during the training processing(a) MDJ station; (b) BJT station.

图3 测试集混淆矩阵热力图(a) MDJ台; (b) BJT台.Fig.3 Heatmaps showing confusion matrix of testing datasets(a) MDJ station; (b) BJT station.
的接收函数标记为保留,将质量较好的接收函数标记为舍弃,甚至会有某些接收函数在挑选时保留亦或舍弃都可以的情况.根据大多数正确分类接收函数规律训练出的模型,在测试时也会受到人为因素导致的错误标签的影响,这些错误分类的接收函数具有一定的“模糊性”,即使人工挑选也可留可弃,对后续处理影响较小.自动挑选而未被人工挑选的接收函数见图4(d、h),可以看到这些接收函数分布没有明显规律,同时按人工挑选经验,这些接收函数也是可以保留的.
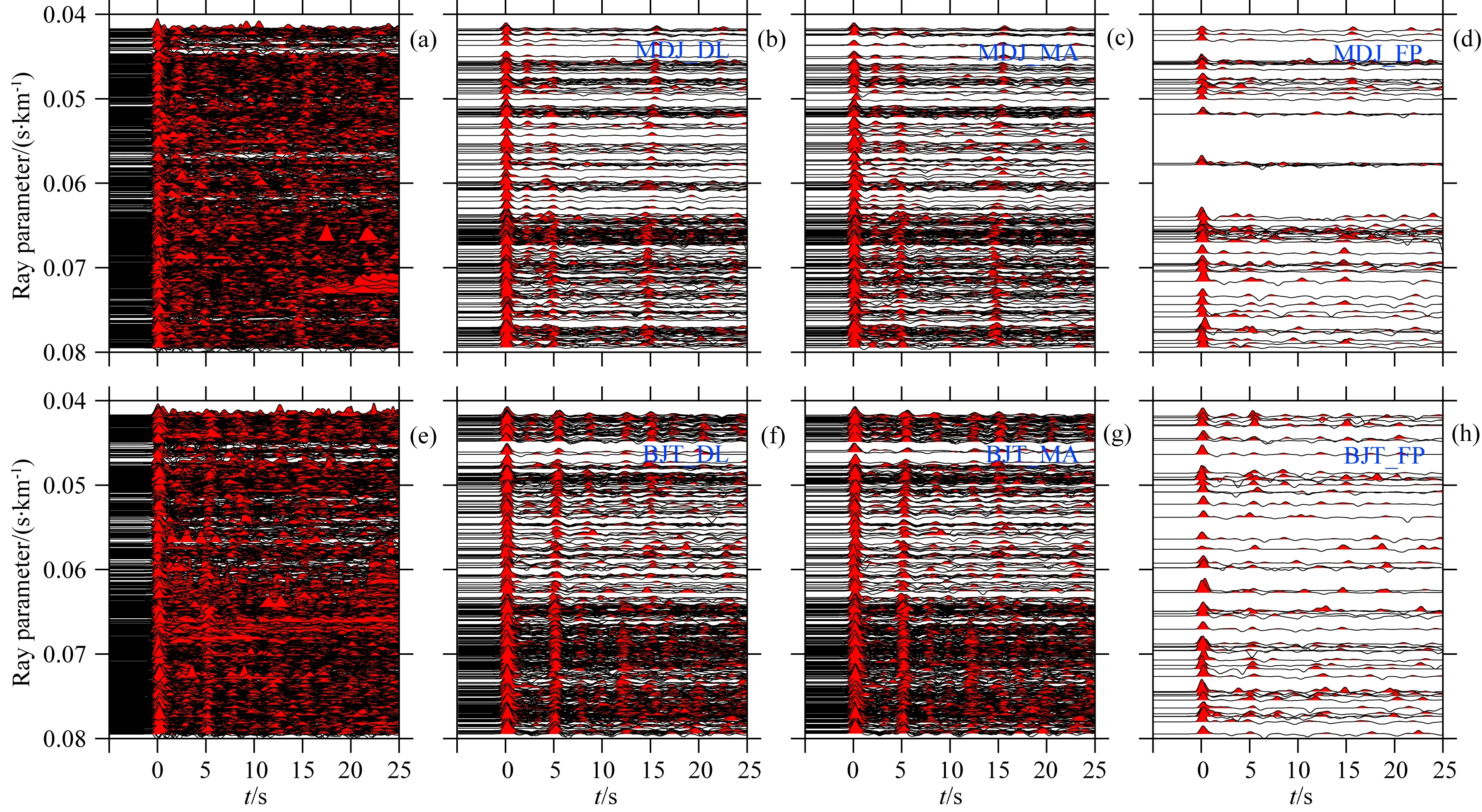
图4 人工挑选与深度学习自动挑选的接收函数结果对比(a) MDJ台原始未挑选的接收函数; (b) MDJ台自动挑选结果(MDJ_DL); (c) MDJ台手工挑选结果(MDJ_MA); (d) MDJ台自动挑选而未被人工挑选的接收函数(MDJ_FP); (e—h)与(a—d)相同,表示BJT台对应结果.Fig.4 Contrast of manual picking receiver functions and deep learning auto-picking receiver functions(a) All receiver functions in testing dataset of MDJ station; (b) Receiver functions of MDJ station after deep learning auto-picking (MDJ_DL); (c) Receiver functions of MDJ station after manual picking(MDJ_MA); (d) Receiver functions of MDJ station remained by deep learning but not manually remained; (e—h) are same as (a—d) but for BJT station.
2 地壳结构与各向异性估计
为验证自动挑选的接收函数在实际处理分析中的有效性,我们分别使用人工挑选的接收函数和自动挑选的接收函数对两个台站下方的地壳厚度、波速比以及方位各向异性进行计算,并对对比结果进行分析.
2.1 地壳厚度与波速比
为估计两个台站下方的地壳厚度以及波速比,我们采用接收函数处理中常用的“H-κ叠加”(Zhu and Kanamori,2000)方法.Ps波、PpPs波以及PpSs+PsPs波相对于P波的时差(tPs、tPpPs、tPpSs+PsPs)可以表示为地壳厚度、地壳纵横波速度比和射线参数的函数.将一个台站的所有接收函数按照公式(3)进行叠加,即可估计台站下方地壳厚度H和平均波速比κ.式(3)中,Ai为第i个接收函数对应时差的幅值,ω1、ω2、ω3分别为三种震相叠加的权系数,MDJ台权系数设为0.7、0.2和0.1,BJT设为0.8、0.1和0.1,N为该台站参与叠加的接收函数的数目.
+ω3Ai(tPpSs+PsPs)}.
(3)
图5(a、d)分别为MDJ台和BJT台测试集通过深度学习算法挑选的接收函数的H-κ叠加结果;图5(b、e)分别为MDJ台和BJT台测试集通过人工挑选的接收函数H-κ叠加结果;图5(c、f)分别为MDJ台和BJT台所有人工挑选的接收函数H-κ叠加结果.图5(a、b、c)对比可以看出不同挑选方案得到的MDJ台下地壳厚度和波速比分别为35.2 km/1.83、34.9 km/1.84、34.8 km/1.84;图5(d、e、f)对比可以看出不同挑选方案得到的BJT台下地壳厚度和波速比分别为38.4 km/1.78、37.9 km/1.79、37.8 km/1.80;
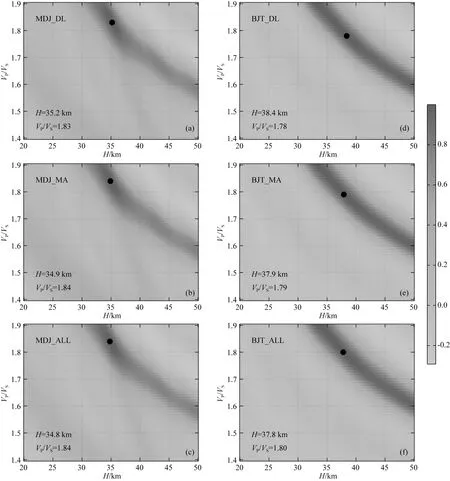
图5 H-κ叠加获得的两台站下方地壳厚度和平均波速比(a) MDJ台自动挑选数据H-κ叠加结果; (b) MDJ台人工挑选数据H-κ叠加结果;(c)MDJ台全部人工挑选数据H-κ叠加结果.(d—f)与(a—c)相同,表示BJT台结果.Fig.5 Crustal thickness and average VP/VS beneath the two stations obtained by H-κ stacking(a) H-κ stacking results using deep learning auto-picking data of MDJ station; (b) H-κ stacking results of manual picking data of MDJ station; (c) H-κ stacking results of all manual picking data of MDJ station; (d—f) are same as (a—c) but for BJT station.
可以看出两个台站经深度学习挑选的接收函数H-κ叠加结果和人工结果基本一致,说明神经网络用于接收函数的自动挑选具有较好的适用性.
2.2 地壳各向异性
我们进一步使用接收函数Ps震相估计台站下方的地壳方位各向异性.在单层水平地壳假设下,接收函数Ps转换波与直达P波的到时差可以由反方位角余弦表示(Liu and Niu, 2012; Zheng et al., 2018),公式如下:
(4)
式(4)中,t为接收函数Ps转换波与直达P波的到时差,t0为各向同性介质假设下的到时差,Δt为各向异性介质产生的到时差,dt是表征地壳各向异性强度的横波分裂后快慢横波到时差,Φ是表征地壳各向异性快轴方向的快横波极化方向,Baz为反方位角.我们需要估计的即是t0、dt、Φ三个参数.在本研究中,参数估计利用遗传算法(Holland, 1992)进行,采用二进制编码,每个参数由八位二进制表示,总基因长度为24,t0、dt、Φ三个参数范围分别设置为4~8 s、0~0.8 s、-90°~90°,所有接收函数Ps转换波振幅值之和作为适应度函数,用公式表示为:
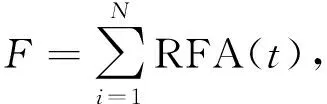
(5)
式中F为适应度函数,RFA(t)表示Ps转换波振幅值,t由式(4)表示.种群设置为50,遗传100代截止,交叉概率和变异概率分别设置为0.6和0.05.
接收函数预处理采用Zheng等(2018)提出的方法,为消除不同震中距对到时差的影响,Ps震相经过了动校正处理.接下来对接收函数进行叠加平均,使用平均后的接收函数估计各个参数.
图6(a、e)分别为MDJ台和BJT台通过深度学习方法从测试集中挑选出的接收函数通过遗传算法估计t0、dt、Φ三个参数的进化图;图6(b、f)为图6(a、e)各向异性估计结果所对应的接收函数Ps波理论到时差曲线;图6(c、g)分别为MDJ台和BJT台人工从测试集中挑选出的接收函数通过遗传算法估计t0、dt、Φ三个参数的进化图;图6(d、h)为图6(c、g)各向异性估计结果所对应的接收函数Ps波理论到时差曲线.将两台各向异性对比结果绘制在图7所示的地形图上,可以看出人工挑选的接收函数和深度学习挑选的接收函数估计出的各向异性结果比较一致.
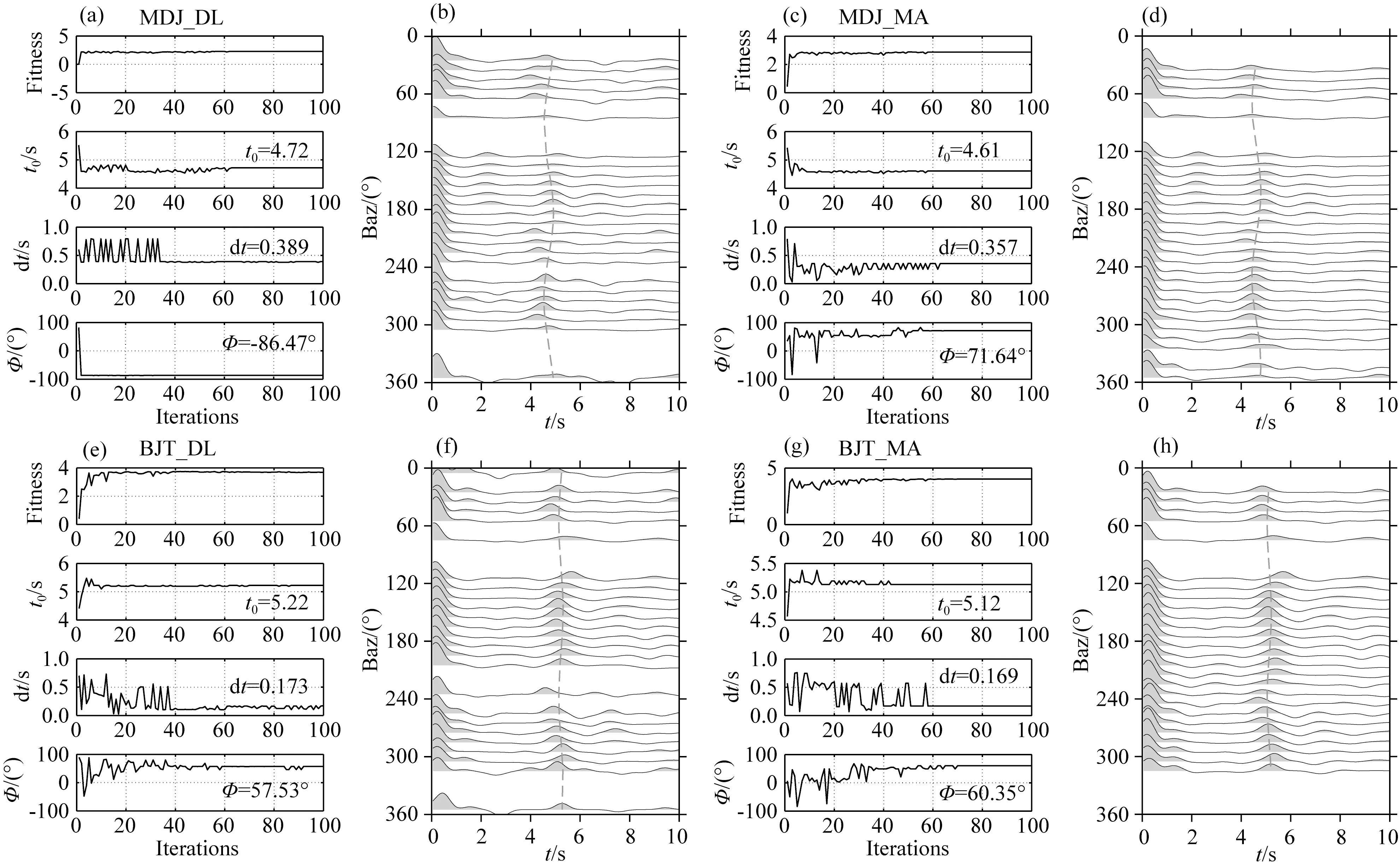
图6 两台站下方地壳方位各向异性结构(a) MDJ台自动挑选出的接收函数,采用遗传算法(GA)估计各向异性时的适应度函数以及各向异性参数变化; (b) 与各向异性参数估计结果相对应的Ps波理论到时差; (c—d)与(a—b)相同,表示MDJ台人工挑选的接收函数计算结果; (e—h)与(a—d)相同,表示BJT台自动、人工挑选出的接收函数估计各向异性结果.Fig.6 Crustal azimuth-anisotropy structure beneath the two stations(a) The variation of fitness, anisotropic parameters in genetic algorithm (GA) using deep learning auto-picking receiver functions of MDJ station; (b) Theoretical Ps wave delay time corresponds to estimated anisotropic parameters; (c—d) are same as (a—b) but use all of manual picking receiver functions of MDJ station; (e—h) are same as (a—d) but for BJT station.
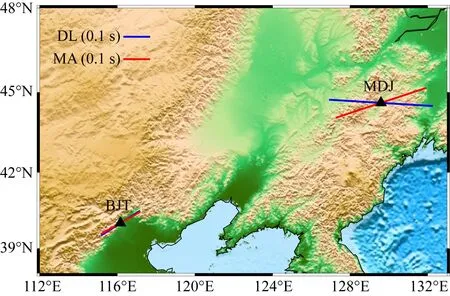
图7 台站所在位置及图6中获取的各向异性结果对比蓝色实线为自动挑选的接收函数估计的结果,红色实线为人工挑选的接收函数估计的结果.Fig.7 Locations of the two stations and the contrast of anisotropic results obtained from Fig.6Blue lines represent the estimations from deep learning auto-picking receiver functions and the red lines are anisotropy results from all of manual selection receiver functions.
3 讨论
3.1 训练集数目的影响
前文我们使用了2000—2016年16年的接收函数作为训练集,2017—2019两年的接收函数作为测试集,测试集与训练集之比接近1∶ 7,最终模型自动挑选接收函数可以达到较好的精度.然而,对于布设时间较短的流动台站或其他临时台站,无法提供大量的数据以供训练.为此我们探究了只应用较小规模的训练集是否也能达到较好的效果.我们重新划分训练集规模进行训练,剩余数据用作测试集进行试验.
表1为MDJ台不同训练集大小的训练结果,训练集规模从552条接收函数递增,最终增加到13531条.最终训练模型应用于测试集后准确率均达到了90%以上,召回率70%以上.同时我们发现,对于召回率,测试集规模过大反而导致了召回率呈下降趋势,仅用一年的数据训练的模型,准确率保证的前提下,召回率反而得到了提升.经过分析,我们发现导致这一现象的原因是对于较小规模的训练集,其正类样本所占比例较高,表1 中Remained一列表示训练集中正类样本所占的比例.如此一来,小规模训练集能够获得相对更好的挑选效果,这一前提为流动台站采取此类方法提供了可能.
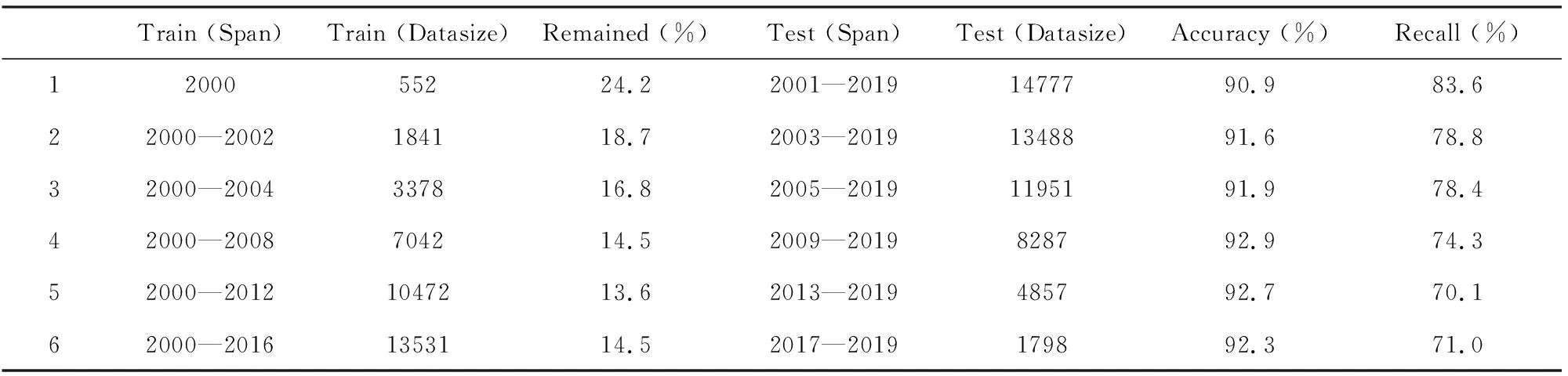
表1 MDJ台不同训练集规模情况下的测试集准确率和召回率Table 1 The influence of testing data size on accuracy and recall of MDJ station
3.2 深度学习方法在<5.5级地震接收函数挑选的作用
在本研究中使用了近20年时间跨度的地震数据,使得我们可以通过统计学对接收函数挑选中所使用的地震震级情况进行分析.如图8所示,MDJ和BJT台站接收到的震级范围M5.1~5.5的事件占比分别为64.5%和64.7%,占比明显高于震级≥M5.5的事件,但是从震级范围M5.1~5.5的事件中人工挑选出的接收函数分别只占到该震级范围内总事件数的2.5%和7.07%,而从震级≥M5.5的事件中挑选出的接收函数占比达到了23.21%和16.29%,意味着在人工挑选过程中,是没有必要花费大量精力挑选 图8 不同震级范围计算的接收函数统计分析(a) MDJ台; (b) BJT台.角标Y代表保留,N代表舍弃.Fig.8 Statistical analysis of receiver functions in different magnitude range(a) MDJ station; (b) BJT station. The subscript “Y” denotes being remained, “N” denotes being abandoned. 由于人工挑选数据的局限性舍弃掉的小震级接收函数数据,在使用自动挑选时则可以得以保留.采用深度学习自动挑选接收函数时,不需要担心人工成本的问题.应用训练好的模型可以快速从小于5.5级的地震事件中挑选出少量较高质量的接收函数,从而提高数据的利用率. 对于永久台站,可以选取每个台站几年的数据进行训练,将所有模型建立一个台网字典供以后直接使用.但是对于大量的流动台站,其观测周期较短,单台接收函数训练结果泛化能力有较大的局限性,此时采用多台数据联合训练,建立一个公共的模型是有必要的. 受台站数目限制,本次研究仅对上文使用的两个台站进行联合训练测试.我们将MDJ台和BJT台的训练集合并,测试集合并,同样经历30000次训练,最终得到的模型应用于测试集准确性达到了92.5%,召回率达到81.3%,再次使用H-κ叠加方法对台站下方的地壳厚度和各向异性进行估计,如图9所示,得到MDJ台下地壳厚度为35.2 km,平均波速比为1.83;BJT台下地壳厚度为37.9 km,平均波速比为1.79.两台最终计算结果与人工挑选的接收函数计算结果或单台自动挑选的接收函数计算结果均较为一致,表明建立区域多台联合接收函数挑选模型具有一定可行性.更多台站准确分析结果需要后续工作继续跟进. 图9 双台联合训练自动挑选的接收函数H-κ叠加结果(a) MDJ台; (b) BJT台.Fig.9 H-κ stacking results of two stations using joint training sets(a) MDJ station; (b) BJT station. 本文发展了一种基于深度学习的接收函数自动挑选方法,参照LeNet5模型构建CNN神经网络,并使用中国地震局MDJ台和BJT台的事件波形提取接收函数,构建训练集和测试集进行验证.实际数据应用结果表明,利用本文提出的深度学习自动挑选接收函数方法具有较高的准确率.对于自动挑选的接收函数,我们使用H-κ叠加方法和Ps震相到时差计算了两个台站下方的地壳厚度、平均波速比以及地壳方位各向异性等地壳参数,得出以下结论: (1)本文提出的深度学习方法挑选的接收函数和人工挑选的接收函数估计的地壳厚度、平均波速比和方位各向异性结果基本一致,证明了本文提出的自动挑选方法的可行性. (2)本研究提出的方法在构建训练集过程中,对训练集数据数量有较低的依赖,试验中尽管只应用几百条接收函数训练,应用最终模型挑选上万条接收函数也可达到90%以上准确率和80%以上的召回率. (3)本研究提出的自动挑选方法可以应用于5.1~5.4级远震,有效地提高了观测数据的利用率,为后续的分析、研究提供更好的约束. (4)对于流动台站,同时使用多个台站的数据构建训练集以提高泛化能力,最终模型在测试集的表现也让人满意. 致谢感谢IRIS网站提供的地震数据(http:∥ds.iris.edu),感谢吉林大学朱洪翔博士提出的宝贵意见,感谢审稿专家给出的修改意见.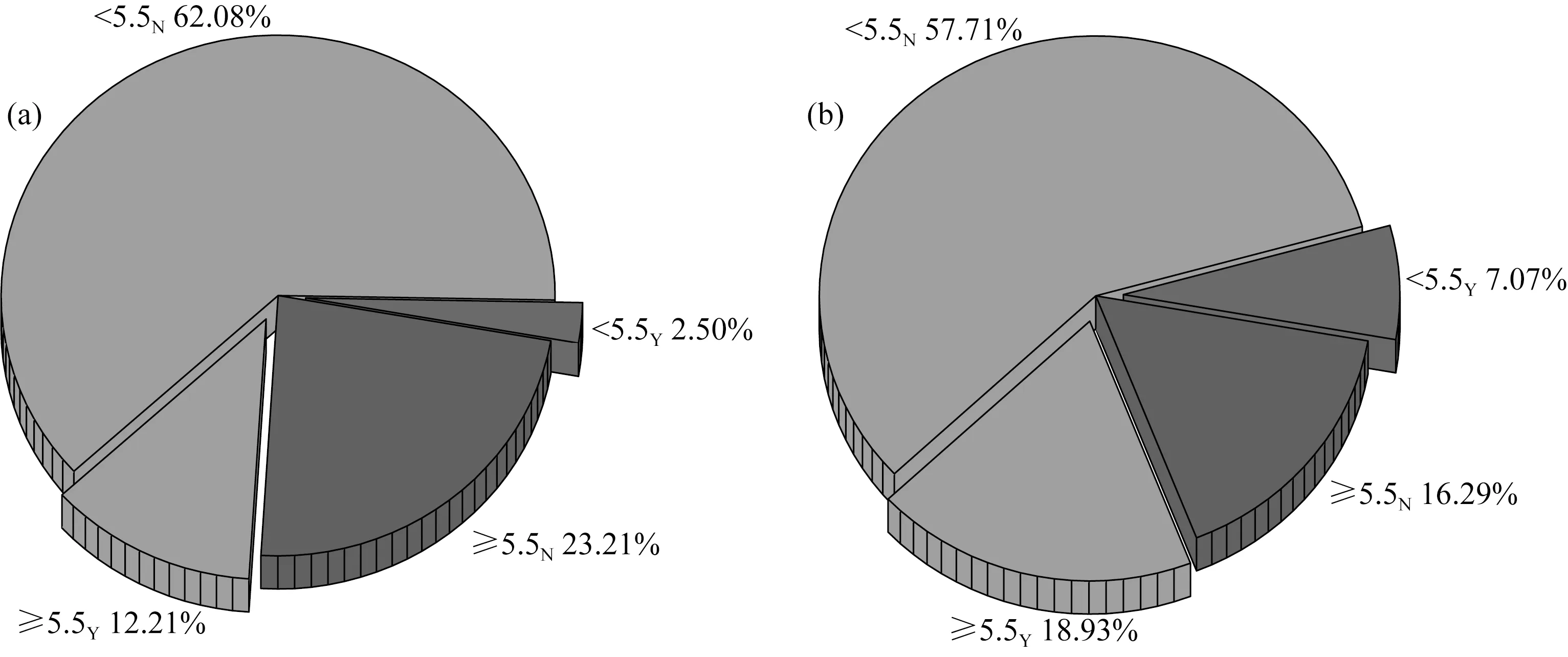
3.3 多台联合训练

4 结论

