带客户分级和需求可拆分的生鲜车辆路径问题
夏扬坤,邓永东,庞 燕+,王忠伟,高 亮
(1.中南林业科技大学 物流与交通学院,湖南 长沙 410004;2.华中科技大学 数字制造装备与技术国家重点实验室,湖北 武汉 430074)
0 引言
生鲜农产品如蔬菜、水果、肉类及水产品等作为生活必须品,已成为当下民生领域的关注焦点[1]。与欧美发达国家相比,我国生鲜农产品实际物流运作水平整体相对落后,依旧以传统粗放型物流配送方式为主。车辆路径问题[1](Vehicle Routing Problem, VRP)是物流配送的核心环节,采用现代智能优化技术对生鲜农产品物流配送路径优化[2]进行研究,对于提高物流配送效率[3]、降低配送成本[4]等均具有重要意义。如文献[1-10]对生鲜VRP(Fresh VRP, FVRP)进行了相关研究,从这些研究可知:FVRP与一般VRP有着明显的不同,生鲜农产品具有易腐蚀、高损耗等特点,其生鲜度会随着配送时间的推移而降低,因此配送具有时间依赖性。在生鲜农产品物流配送中应该考虑生鲜损耗费用,在权衡配送成本的同时考虑降低生鲜损耗。
现代生鲜物流市场竞争激烈,配送企业要想在激烈的市场竞争中立于不败之地,就必须保证一定的优质客户资源,协调处理好客户关系维护问题[11-12]。文献[13-15]在研究带软时间窗的VRP(VRP with Soft Time Windows, VRPSTW)时,对考虑客户满意度的VRP(VRP with Customer Satisfaction, VRPCS)进行了探讨,研究认为,在VRPSTW模型中考虑客户满意度因素有利于提升配送企业的服务质量,促进企业可持续发展。当配送资源受限时,对客户实施分级处理,优先考虑重要客户的服务要求,更有利于配送企业维护好优质客户资源。在物流配送实践中,配送企业的大订单资源通常来自于少数重要客户,这些少数客户常能占据配送企业80%以上的年度业务量,有时一个大客户企业的年度订单收益完全可以超越上百个小客户的总和,而且针对少数重要客户进行战略合作,在单位业务收益的客户关系维护时间成本方面也更为节约。考虑到VRPSTW容易降低客户满意度,而配送企业在提供配送服务时必然需要权衡成本与收益,因此在能够界定客户重要性的情况下,配送企业可以对客户的重要性进行分级处理,优先满足重要客户的期望时间窗。通过增大重要客户的时间窗偏离量惩罚程度,引导算法求解时尽可能地优先满足重要客户的时间窗,形成一个考虑客户分级的VRPSTW(VRPSTW with Customer Classification, VRPSTWCC)。
需求可拆分VRPSTW[16](VRPSTW with Split Deliveries, VRPSTWSD)是VRPTW的一个新研究方向,对客户需求进行合理的拆分配送能够提高车辆装载率,降低物流配送成本。在以往的VRPSTWSD研究中,常假设客户需求量可按照计量单位来连续单元化拆分,对需求离散拆分的VRPSTWSD(VRPSTW with Discrete Split Deliveries, VRPSTWDSD)的研究很少。但在连锁超市配送、快递配送等过程中,为了方便装卸作业,配送企业通常会将客户的订单需求按照一定的特性划分来打包装箱,而且不同产品的装箱量通常是有差异的,农产品一旦进行打包作业形成了“背包”,则很难再对单个背包重新拆分组装,若拆分则只可能依“背包”进行拆。在多品种生鲜农产品配送实践中,每个客户点可能有多种生鲜农产品品种需求,且每一种农产品的需求量可能不同,一般同种产品不适合拆分送达,若将单种农产品的需求量看成一个不可再拆分的“背包”,则客户需求可视为由多个背包离散组合而成。本文将“背包”定义为“不可进一步拆分的客户需求量的最小集合”,将结合客户需求依背包拆分的特点,对客户点与背包施行统一操作,针对客户点与背包都设计相应的邻域操作算子,尽可能地降低由于需求拆分引发的求解难度。
VRP是NP-hard问题,当VRP中需求可拆分时求解难度会更大,大规模问题适合采用启发式算法进行求解。由于一般的经典启发式算法不具备全局寻优能力,学者们通常采用智能优化算法进行求解[17]。禁忌搜索(Tabu Search, TS)算法[18-19]是一种模仿人类智能思维的智能优化算法,其邻域搜索能力较强,可以使用短期禁忌表来记忆相应的禁忌信息,避免搜索重复的解决方案,提升搜索效率。从已有的VRP文献[20-21]来看,TS算法具有简单性、易操作性、适应性、高效性等优点,是一种求解VRP的高效智能优化算法。因此,本文也以TS算法为框架来设计改进算法。
目前,学术界针对需求依背包拆分VRPSTW(VRPSTW with Split Deliveries by Backpack, VRPSTWSDB)的研究较为少见,而对于带客户分级和生鲜损耗费用的VRPSTWSDB(VRPSTWSDB with Customer Classification and Fresh Loss Cost, VRPSTWSDBCCFLC)的公开报道文献尚未见到。因此,本文对VRPSTWSDBCCFLC这类新的问题类型进行研究,并设计一个带动态禁忌表的自适应禁忌搜索算法(Adaptive Tabu Search Algorithm with Dynamic Linear Tabu List, ATSA-DLTL)进行求解。
1 数学模型构建
1.1 问题描述
本文对VRPSTWSDBCCFLC进行研究,具体可描述为:配送中心使用一定数目的车辆对各客户进行生鲜农产品配送后返回出发点,需要求得一组合理的车辆配送路线,并最小化车辆使用数量、行驶时间、生鲜损耗、等待时间及时间窗偏离量等对应的费用。其中,车辆不许超载,每个客户点的生鲜农产品需求量必须满足,客户需求若拆分则只能依背包来离散拆分配送,配送中心点i=0的硬时间窗约束[0,Tmax]不许违反。另外,每个客户点i∈V′的期望时间窗[ai,bi]可通过施行惩罚来实现软时间窗,软时间窗的处理方式为:早到需等待至时间窗开启再进行卸货作业并需要支付等待费用,迟到则可以立即进行卸货作业并需要支付惩罚费用。
在生鲜农产品物流配送中,客户的需求位置分布具有分散性,需求时间也具有差异性。如在城市生鲜农产品物流配送中,一个农产品生产基地(如城市蔬菜生产基地)每天都要为众多生鲜农产品需求点(客户点)进行供货,这些客户通常分布于城市的各个街道小区内,位置非常分散,配送网络庞大且每个客户点都会根据自身情况而提出不同的期望时间窗,其路径优化难度很大。为了简化问题,本文将生鲜农产品物流网络抽象为一个连通图,假设各点之间均可互通,点之间的行驶时间符合三角不等式,忽略天气、交通堵塞等其他因素带来的影响。为了方便模型描述,定义VRPSTWSDBCCFLC的数学模型的符号,如表1所示。

表1 VRPSTWSDBCCFLC数学模型的符号定义
1.2 数学模型
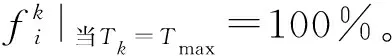
(1)

(2)
(3)
配送系统的生鲜损耗费用Z4,
(4)
另外,VRPSTWSDBCCFLC模型中需对客户的重要性进行分级,不同级别的客户,其单位时间窗偏离量的费用ci不同,重要客户对应的ci值应该更大,即尽可能地保证重要客户的期望时间窗。结合帕累托定律[17],约定客户群中含有20%的重要客户(当0.2N非整数时则将重要客户的数目向上取整为⌈0.2N⌉)。
综上所述,结合以往带时间窗VRP相关模型[22-24],本文给出VRPSTWSDBCCFLC的双目标数学模型如下:
minG(y)=p1K+p2Z。
(5)
Z=Z1+Z2+Z3+Z4,
(6)
(7)
(8)
(9)

(10)
s.t.
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)

(25)

(26)

(27)

(28)
式(5)表示双目标函数,其中参数p1与p2为定性概念,只表示权重p1》p2,即第一目标“最小化车辆数”相对于第二目标“最小化行驶费用”具有绝对优先权;式(6)表示行驶费用(在行驶过程中引发的费用);式(7)表示行驶时间费用;式(8)表示因早到等待引发的时间窗偏离量费用;式(9)表示因迟到立即服务引发的时间窗偏离量费用;式(10)表示配送系统的生鲜损耗费用。式(11)为车辆的装载能力限制;式(12)为配送中心的硬时间窗限制;式(13)为车辆k在点i的等待时间;式(14)表示车辆k到达点j的时刻;式(15)~式(19)表示各客户的需求量必须全部满足,客户点的需求可拆分,但单个背包量不可再拆,即客户需求只能通过依背包离散拆分来实现分批多次配送;式(20)~式(21)为各顶点进出车辆流平衡约束;式(22)~式(23)表示全部车辆从配送中心出发后最终都返回原出发点;式(24)可消去子回路;式(25)可用于估算车辆数的下界;式(26)~式(28)为变量的取值范围。
2 禁忌搜索算法设计
基本TS算法[22]前期具有较强的禁忌能力和寻优速度,但在中后期容易因禁忌过度而难以搜索到更好解。基本TS算法对多约束多极值的NP-hard问题易陷入局部最优,一般需在算法中设计一些有效的禁忌策略和邻域搜索策略来增强寻优能力。本文在基本TS算法基础上,构建一个动态禁忌表,设计一个多邻域结构体,嵌入自适应惩罚机制,采用禁忌表重新初始化等策略来增强其自适应寻优能力,从而形成了一个ATSA-DLTL进行求解。
为方便算法描述,定义相关符号,如表2所示。

表2 ATSA-DLTL的相关符号定义
2.1 解的表示与初始解
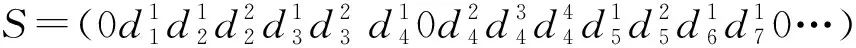
采用“最近0法”来生成初始解,可行初始解的具体生成方式为:在车辆装载能力Q和路线的最长工作时间Tmax约束下,按照各客户点到配送中心点0的距离依次将客户的背包加入车辆路线中,约定初始解不考虑拆分,即初始解中同一点的背包均添入同一车辆路线。
2.2 解的评价设计
ATSA-DLTL取总的评价函数G如式(29)所示:
G=p1K+p2F。
(29)
式中参数p1与p2只表示两个目标的权重p1》p2。
行驶费用评价函数F如式(30)所示:
F=Z+Z′。
(30)
式中Z′表示违反约束最长工作时间Tmax限制的惩罚费用。
文献[22]指出,接受部分违反约束的邻域解有利于算法对邻域进行充分搜索,也有利于算法从不可行的当前解过渡到更好的可行解。但若是对不可行解接受过度,则容易产生大量的不可行解,反而不利于寻优进程。因此,为了在不可行解与可行解之间寻找到一个较好的平衡,ATSA-DLTL对不可行解的接受范围进行控制,约定候选解(当前解是从候选解中挑选出来的)不能违反载重约束,即候选解只能接受部分违反最长工作时间Tmax限制的邻域解,惩罚值Z′如式(31)所示:
(31)
式中:δk为第k条路线的工作时间超出量;H为一自适应惩罚系数。
ATSA-DLTL对H的取值方式进行调整,具体如下:
记Λ1与Λ2为整型计数变量,且Λ1,Λ2∈[0,15],初值都取为0。在接连迭代过程中,每次当选出的“当前解”Snow为不可行解时,便让Λ1加1,否则让Λ2加1,若Λ1或Λ2取值超出范围[0,15],则设为0。参数H可引导算法的搜索方向。H代表超出最长工作时间Tmax限制的自适应惩罚权重系数,通过实验将取值范围限定为H∈[5,1 000],H的初值取为5,当超出范围时取最小值;当Λ1=15时,将H乘以δ;当Λ2=15时,则将H除以δ,δ的取值如式(32)所示:
δ=2+rand()。
(32)
根据以上规定,记Hθ为第θ次迭代中H的取值,则当H值发生变化时,其第(θ+1)次迭代的取值Hθ+1如式(33)所示:
(33)
式(32)中的δ为H设置的一个随机伸缩变换系数,其中rand()为区间[0,1]内的随机数。ATSA-DLTL在自适应参数H内引入随机数δ,可使H的取值具有多样性,增强对邻域的扰动,有利于新解的丰富性,引导算法在可行解与不可行解之间自适应地变换,提升ATSA-DLTL的全局寻优能力。
2.3 解改进策略设计
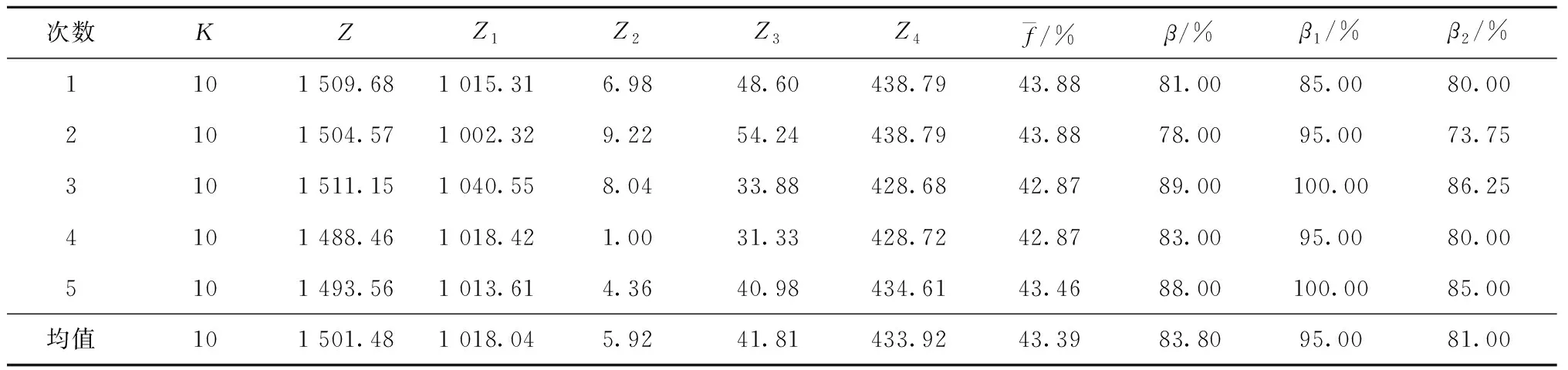
本节取邻域解的数目上限为P=60+N(对应了邻域搜索终止条件),采用一种“解改进”策略来挑选“最好解”Sbest与“当前解”Snow,以加速算法寻优进程。结合两级评价指标K与F分层来评价优化解,在邻域解的生成过程中,若某个“可行候选解”Sfeasible比“最好解”Sbest更优,即当满足“K(Sfeasible) 若在邻域搜索中不存在“可行候选解”Sfeasible优于原“最好解”Sbest,则Sbest保持不变,只需挑选新的Snow。由于部分候选解可能被禁忌,此处Snow分两种情况进行挑选:若存在“非禁忌候选解”Snon-tabu,则挑选出“最佳非禁忌候选解”#Snon-tabu,并将其设定为新Snow;若全部候选解都被禁忌,则挑选出“最佳候选解”#Scandidate,并释放该#Scandidate(即消去其禁忌),同时将此#Scandidate设为新Snow。这里#Snon-tabu、#Scandidate都是结合两级评价指标K与F分层挑选,不再赘述。 ATSA-DLTL设计“最长工作时间路线扰动规则”(PRMDR)来辅助挑选两相异路线R1与R2,PRMDR含有的一个显著特点为“最长工作时间路线超限必选”策略,此举可以较好地配合ATS-DLTL算法的自适应惩罚机制,尽可能地减少对无效解集的搜索。具体的路线挑选方式为:当最长工作时间路线(R*)的长度值T(R*)=max(Tk)>Tmax时,令R1=R*,然后在其余路线内再随机挑选出一条作为路线R2;当R*的长度值T(R*)=max(Tk)≤Tmax时,便仍采用随机方式挑选出两条相异路线R1与R2。 以往的TS算法[22]常采用N×N阶的方阵禁忌表,但方阵禁忌表禁忌容量过大,虽在迭代前期能够加速算法寻优,但随着迭代次数的增加,容易造成对优良候选解的禁忌过度。 本文ATSA-DLTL设计一个动态禁忌表(Dynamic Linear Tabu List, DLTL),大小取为l×3阶动态线性表,以邻域交换中的客户点对(i,j)为禁忌对象。其中:第1,2列存储邻域操作的客户点对(i,j);第3列则存储对应的禁忌长度值ζ。当客户点对(i,j)所对应的候选解被选择为下次迭代的“当前解”时,就在禁忌表的对应位置填入禁忌信息,约定禁忌长度ζ每次迭代都可取5~16之间的随机整数。规定禁忌对象每次迭代后都要将禁忌长度减1,直到降为0才可解禁。ATSA-DLTL允许禁忌表的长度l随迭代而动态取值,将其长度l取值为:在迭代的前Nu0步以内取为N,在Nu0步后每隔u次迭代,就使l在区间[5+N/20,5+N/10]内取随机整数值。 另外,增设一定的重新初始化策略,以增强算法的寻优能力。ATSA-DLTL再设计一个“禁忌表重新初始化”策略,约定在迭代Nu0步以后,每隔u次迭代就重新初始化禁忌表。本文取Nu0=500+10N,u=40。 ATSA-DLTL共含有3个迭代的终止条件,约定只要满足条件之一便使算法终止迭代,具体为:①当“实际总迭代次数”Mu1达到预设的上限值Nu1;②当“最好解”保持连续不变的迭代次数Mu2达到预设的上限值Nu2;③当计算机CPU的运行时间Mu3达到预设的上限值Nu3。经综合考虑,ATSA-DLTL取Nu1=4 000+80N,Nu2=3 000+5N,Nu3=600+12N。 ATSA-DLTL的基本算法流程如图1所示。 本文使用MATLAB 2014a进行编程,并且在LENOVO®V3000,CUP为2.40 GHz,内存为4 GB的AMD笔记本上测试ATSA-DLTL。目前,尚无VRPSTWSDBCCFLC的研究文献,自然也没有对应的标准测试算例。以往学者们常采用Solomn算例[22-24]作为标准算例来求解VRPTW,本文以含N=100个客户点的Solomn算例[21-23]来构建VRPSTWSDBCCFLC的相应算例。根据Solomn算例的数据特点,以点间的欧氏距离代表点间的行驶时间。结合帕累托定律[17],从算例中挑选出20%的客户作为重要客户,为方便描述,直接将原始算例中前20%的客户作为重要客户,取前20个客户的ci=0.5(1≤i≤20),后续客户的ci=0.1(21≤i≤100)。另外,将客户需求量随机拆分为1~4个背包量(R=4)并固定下来,由此便可得到所需要的算例。本文以其中的算例R111为例进行VRPSTWSDBCCFLC测试分析。 (1)VRPSTWSDBCCFLC求解结果 以Solomn算例中的R111为例来进行VRPSTWSDBCCFLC类型测试分析,测试平台不变,对算例R111进行5次测试,并记录相关结果。采用“最近0”法求得的“初始解”Sinitial结果如表3,由于“最近0”法每次求得的“初始解”(可视为原始人工计划方案)都一样,因此本文只给出一次测试结果。以ATSA-DLTL对“最近0”法得到的“初始解”进行优化,求得的“最好解”Sbest结果如表4。 表3 “最近0”法求得的“初始解”结果 表4 ATSA-DLTL求得的“最好解”结果 (2)计算结果分析 1)整体费用指标的改进效果分析。 以VRPSTWSDBCCFLC类型为例,对求得的“最好解”与“初始解”稍作比较分析。ATSA-DLTL以“最近0”法求得的“初始解”来进行深度优化,“最近0”法属于一种经典启发式算法,简单易行,便于人工快速规划配送路线,但求解效果通常较差。ATSA-DLTL属于一种智能优化算法,现对二者进行比较。 表5给出了“最近0”法和ATSA-DLTL的相关均值的对比结果。从表5中可以明显发现,ATSA-DLTL算法相比“最近0”法,其在车辆数(K)、总行驶费用(Z)、行驶时间费用(Z1)、早到的等待时间费用(Z2)、迟到的时间窗惩罚费用(Z3)及生鲜损耗费用(Z4)等各项指标都表现出了绝对的改进优势。ATSA-DLTL对“初始解”的改进效果十分明显。 表5 相关费用指标的改进结果 2)考虑客户分级的效果分析。 由于“最近0”法只是在考虑车辆载重与路线工作时间限制的情况下,按照距离点0的远近来构建初始方案(初始解)。因此,不论配送企业[28]是否对客户进行分级处理,初始解都不会优先考虑满足重要客户的时间窗。由表3与表4可知,在“初始解”Sinitial中有β1(Sinitial)<β(Sinitial)<β2(Sinitial),重要客户的时间窗满足率(β1)比全部客户的时间窗满足率(β)和非重要客户的时间窗满足率(β2)都要低。 虽然初始解中没有考虑优先满足重要客户的时间窗,但经过ATSA-DLTL优化后,在各次测试求得的“最好解”结果中有β1(Sbest)>β(Sbest)>β2(Sbest),即重要客户的时间窗满足率(β1)成为了最高的。可见,在求解算法中考虑客户分级,可以引导算法尽可能地优先满足重要客户的时间窗。另外,在“最好解”中,不仅重要客户的时间窗满足率(β1)得到了提高,全部客户的时间窗满足率(β)和非重要客户的时间窗满足率(β2)也都得到了提高,说明ATSA-DLTL相比“最近0”法在减少配送成本的同时还能提升整个配送系统的客户满意度。本文的VRPSTWSDBCCFLC模型确实有助于在提升重要客户满意度的同时综合优化配送成本。Sbest相对于Sinitial在时间窗满足率上的改进程度如表6所示。 表6 相关时间窗满足率的改进结果 3)考虑生鲜损耗费用的效果分析。 表7 相关生鲜指标的改进结果 虽然目前尚未有VRPSTWSDBCCFLC类型的研究文献,但符卓等[22]对需求依订单拆分的VRPSTW(VRPSTW with Split Deliveries by Order,VRPSTWSDO)进行了研究,若将其文中的订单当成本文的背包,则其相当于研究了一种需要依背包拆分的VRPSTW(VRPSTWSDB)。因此,为了进一步说明本文ATSA-DLTL的优化性能,采用VRPSTWSDB类型作为文献对比分析。在利用VRPSTWSDBCCFLC模型求解VRPSTWSDB时,统一全部客户的重要性,并在行驶费用中去掉生鲜损耗费,即在采用ATSA-DLTL求解时,令全部ci=0.1(1≤i≤100)且Z4=0。 符卓等[22]设计了一个禁忌搜索(TS)算法,并采用含100个客户点的Solomn算例进行了测试,其在对C1类算例(文献[22]只给出了7个算例的结果)的测试结果中求得了满足时间窗的结果。本文也采用C1类型算例(含C101~C109共计9个算例)对VRPSTWSDB进行测试分析,每个算例测试5次,取最好结果。虽然测试的是VRPSTWSDB类型,但计算结果显示,本文ATSA-DLTL在对C1类型的求解结果中都获得了满足硬时间窗的结果(即9个算例都求得了β=100%),该结果可与符卓等[22]的结果进行直接比较分析。另外,Belfiore等[23]和Shi等[24]分别采用分散搜索(Scatter Search, SS)和混合遗传算法(Hybrid Genetic Algorithm, HGA)对带硬时间窗的VRP(VRPHTW)进行了测试,其对C1类算例的测试结果也可与本文结果进行间接对比分析。各算法车辆数的对比结果如表8所示,距离值的对比结果如表9所示。 表8 K值的对比结果 表9 距离值的对比结果 续表9 由表8和表9结果可知,本文ATSA-DLTL的求解结果已达到或接近目前世界已知的最好结果。在车辆数方面,ATSA-DLTL与TSA、SS一样,都求得了最少车辆数的结果,比HGA的求解效果要好;在行驶距离方面,ATSA-DLTL都要好于或等于3种对比文献算法,好于TSA、SS及HGA的算例数目分别为1、6及4个,算例的平均距离值相对于TSA、SS及HGA分别节省0.51%、0.73%及0.07%。可见,本文ATSA-DLTL的求解效果优于3种对比文献算法。 农产品具有生鲜属性,将生鲜损耗费用加入行驶费用目标中,有利于降低路途的生鲜损耗,保持生鲜农产品的生鲜程度,维护食品安全。对客户进行分级处理,优先满足重要客户的时间窗,可提高重要客户的满意度,使配送企业尽可能地保持优质客户资源。本文结合需求依背包拆分条件,将客户分级思想融入约束,将生鲜损耗费用纳入行驶费用目标,并以“最小化车辆数”与“最小化行驶费用”分别为第一与第二目标,构建了VRPSTWSDBCCFLC的双目标数学模型。 以“最近0”法生成初始解,并以ATSA-DLTL进行优化。测试结果表明,对客户实施分级处理,通过增大重要客户的时间窗偏离系数,可提高重要客户的时间窗满足率。相比“最近0”法得到的初始解,经过ATSA-DLTL优化后的各项费用指标与生鲜损耗指标都得到了大幅度下降,而各项时间窗满足率指标则得到了提升。ATSA-DLTL在降低配送成本的同时,还可以降低生鲜农产品的生鲜损耗和提升客户满意度。可见,在物流配送中并非增大配送投入成本(如增加使用车辆数)就会提高客户满意度。更新物流优化技术,采用现代智能优化方法对原有配送方案进行优化,具有非常重要的实践价值。 随着电子商务业务和第三方物流配送业务的快速发展,共同配送和协同配送等已成为配送实践中急需要解决的问题。后续,在本文的研究基础之上,将对共同配送和协同配送中涉及的需求可拆分半开放式生鲜VRP这一新问题类型进行研究,并优化算法设计;在禁忌搜索算法的基础之上设计超启发式算法进行求解,进一步改进算法的寻优性能。2.4 多邻域结构体设计






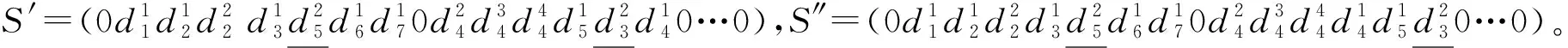
2.3 PRMDR设计
2.4 动态线性禁忌表设计
2.5 迭代终止条件
2.6 算法流程图

3 算法测试
3.1 算例描述
3.2 求解结果分析





3.3 文献对比分析



4 结束语

