考虑不规则物流交互点的过道布置问题建模与优化
刘俊琦,张则强,王沙沙,曾艳清
(西南交通大学 机械工程学院,四川 成都 610031)
1 问题的描述
“工业4.0”概念的提出,使得先进制造业成为未来发展的必然趋势和关键内容。加快发展方式转变,促进工业迈向中高端不仅是建设制造强国的重要举措,也是新常态下打造新的国际竞争优势的必然选择。为取得竞争优势,制造业越来越重视高效低成本生产。设施布局问题[1-6]存在于多种类型的制造和服务系统中,如制造业中生产车间布局[5],服务业中办公区域布局[7]以及医院走廊两侧医务室与病房合理布局[8],合理的布局直接关系到作业效率和运作成本。因此,在制造业、服务业和学术界中,设施布局问题受到广泛关注。
作为设施布局问题的一种特殊形式,过道布置问题(Corridor Allocation Problem, CAP)[9]是一种典型的具有NP-hard属性的组合优化问题,其问题规模的扩大及约束条件的增加均使得精确求解难度大幅增加,因其具有较高的研究价值以及广阔的应用前景,使CAP自提出以来便迅速成为设施布局领域的研究热点。过道布置问题及其混合整数规划(Mixed Integer Programming, MIP)模型是由Amaral等[9]在2012年首次提出并建立的,且应用3种启发式方法求解该问题,验证了该模型的正确性和算法的有效性;Ghosh等[10]应用改进遗传算法及分散搜索算法(Scatter Search, SS)分别对CAP的不同规模问题标准算例进行测试,两种算法在结果上均可以得到高质量的较优解,且后者算法的收敛速度和运行效率均优于前者;Ahone等[11]采用禁忌搜索算法(Tabu Search,TS)和改进模拟退火算法对CAP大规模算例问题进行测试求解,改进模拟退火算法在各方面均表现出良好的求解性能;Kalita等[12]在原始CAP问题模型的基础上,将过道总长度考虑到过道布置问题当中,建立了非线性双目标优化问题数学模型,即设施总长度与设施间物流总成本最优,并应用遗传算法对标准算例进行测试,验证了算法的有效性;毛丽丽等[13]构建了含有总流量入口和通道宽度的混合整数规划模型,同时改进分散搜索算法并进行应用,通过对大规模问题的求解测试发现,所设计算法的求解质量和求解速度均优于分散搜索算法与禁忌搜索算法;为了更符合实际生产情况,管超等[14-15]提出并构建了双层过道布置问题以及双目标混合整数规划模型,并对问题应用花授粉算法与遗传变邻域算法进行求解,结果表明两种算法均能较好地求解过道布置问题。
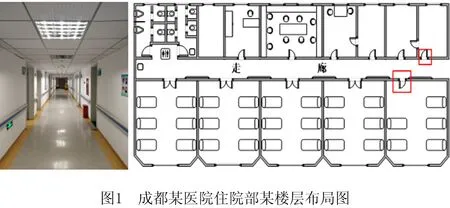
上述文献对于CAP的建模与求解情况虽然已经有了广泛且深入的研究,但仍存在模型过于理想化或求解质量不高以及求解效率欠理想的情况。物流交互点作为设施布局中的重要影响因素,在实际情况中合理的设置可以极大程度地减少运输上的浪费,降低成本。初始CAP在一定意义上将物流交互点抽象成了方便计算的一维坐标点,在加入通道宽度后,演变成二维坐标点,文献[16]探究了物流交互点在Y轴上位置对物流成本的影响。但迄今为止,未有文献考虑设施物流交互点在X轴上不规则布置位置对总物料搬运成本的影响,传统CAP的物流交互点为了简化过道布置问题的计算复杂程度,仅将物流交互点设置在靠近过道边线设施长度的中点,但在实际过道布置问题中,存在物流交互点不规则设置(设施的物料搬运点并非全部设置在靠近过道一侧的设施边线中点处),如图1所示为成都某医院住院部楼层布局图所示,走廊末尾两房间的开门处在房间的角落位置,结合实际调研情况,将实际CAP物流交互点简化成不规则交互坐标,即将走廊末尾两房间坐标点抽象成角点,而非设施在过道边线处的中点。本文以上述不规则交互点问题和过道宽度为研究对象,以含有过道宽度的过道布置问题为研究基础,提出一种扩展的考虑不规则物流交互点的过道布置问题(EXtend Corridor Allocation Problem, EX-CAP),使得过道布置问题更加贴近实际情况,一定程度的降低了物流成本。
鸡群优化(Chicken Swarm Optimization, CSO)算法是由Meng等[17]于2014年首次提出的一种模拟鸡群群体觅食行为的仿生算法,是一种全局优化算法,相比粒子群优化(Particle Swarm Optimization, PSO)算法[18],遗传算法(Genetic Algorithm, GA)[19-21]等一系列寻优算法,具有操作简单、收敛速度快和收敛精度高[22]的优点,且鸡群算法求解过程具有方向特性[23],可以沿着更好的方向寻优。目前,鸡群算法在求解连续函数问题方面已被广泛应用,如轨迹优化[24],非线性系统的参数估计问题[25]、聚类分析问题[26]等优化问题。除此之外,鸡群算法也逐渐被改进并应用于求解离散化问题,如求解0-1背包问题[27]、柔性作业车间调度问题[28]等,参考已有文献,鸡群算法在求解离散化问题上亦能取得了良好的求解结果。但综合对鸡群算法进行离散化处理、编码方式采用实数编码等操作,在设施布局方面的应用尚未有公开报道,因此本文采用鸡群算法来求解过道布置问题。
传统鸡群算法主要解决连续性问题[29],对于高维度问题易出现过早陷入局部最优和早熟收敛的情况[30]。针对这些问题,本文主要从两方面进行改进:①对鸡群算法进行离散化设计,采用遗传算法中的交叉、变异等操作增加解的多样性,防止陷入局部最优;②全局搜索中将鸡群中已分组的个体按照所设定的代数参数G进行重新分组。与此同时,在局部搜索过程,对小鸡位置更新的模块加入定向策略,稳定求解的优化性。综上所述,本文旨在考虑物流交互点在过道边线水平方向上的变动对过道布置以及总成本的影响,根据问题特征,构建符合该特征的混合整数规划模型(MIP),采用LINGO优化器对所提出的模型进行精确求解以验证模型正确性,并设计一种基于遗传的混合鸡群算法(GA-CSO)对EX-CAP问题进行大规模求解。为了更好地说明所提优化算法具有更广泛的适用性,将GA-CSO算法应用到求解原始过道布置问题中并与相关文献进行对比。结果表明,对于所引用初始CAP算例优化,GA-CSO均表现出良好的求解速度和求解质量。
1 考虑不规则物流交互点位置的CAP
1.1 问题描述
在文献[5]的基础上,本文考虑上下两行设施序列末端设施物流交互点的位置对物流成本的影响,假设设施的形状为大小不等的矩形(如图2),已知每个设施在X轴方向上的长度与各个设施间的物流量,将设施间的总物流成本最小作为目标函数,明确排列在通道两侧的设施数目,将设施与一个总流量入口(N+1)按照某种序列随机排列在通道两侧,理想状态下布局不受场地大小以及其他条件限制,且相邻设施之间无间隙,上下两行设施坐标均符合笛卡尔坐标系,最左侧起始点为坐标轴原点O,假定排在末尾的设施物流交互点设置在靠近坐标轴原点的角点上。
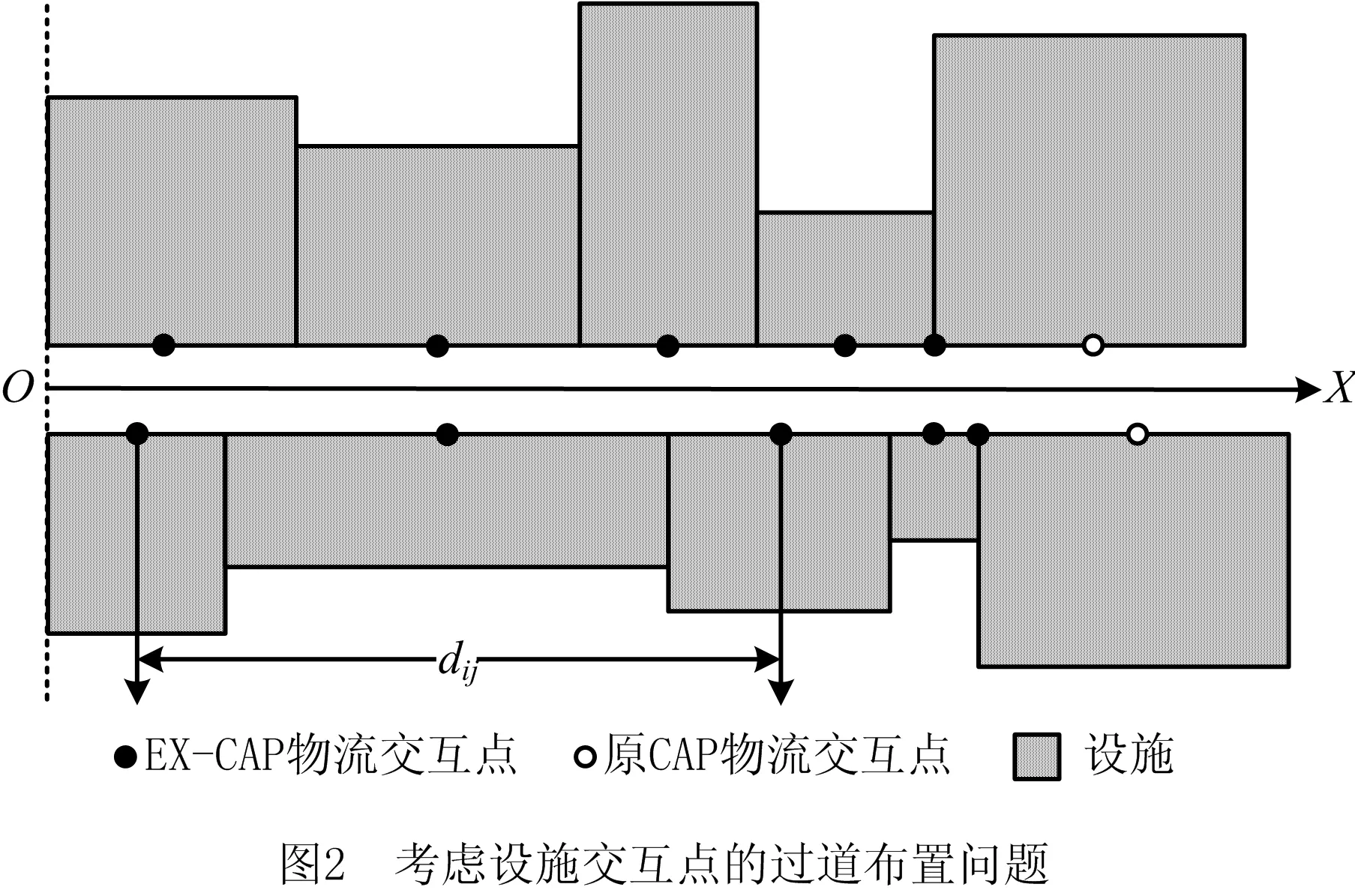
定义参数和变量:
n为问题的规模;
I为所有设施的集合,I={1,2,3,…,n,n+1};
i,j为设施的编号,i,j∈I;
cij为设施间的物流成本;
dij为设施i,j之间物流交互点在X轴方向的距;
w为通道宽度;
li为为设施在通道边线方向上的长度,即设施宽度;
αij为二进制变量,如果设施i,j分配在同一行,且设施被放置在设施j的左侧,则αij=1;否则αij=0;
qij为二进制决策变量,若设施i与设施j在被布置于同一行,则qij=1,否则qij=0。
1.2 EX-CAP交互点位置的约束条件
在CAP中,通常为简化求解方式,基于应用笛卡尔坐标系确定的物流交互点一般设置在设施边线中点,若根据实际情况将物流交互点布置在角点上并建立数学模型则更为复杂,其原因在于对原始CAP问题所建立的数学模型中,均未考虑预先确定的位置上的设施,在求解过程中易简化对两个设施之间距离的求解方式。对此,为进一步考虑交互点位置的过道布置问题(EX-CAP),引入二进制变量β,则物流交互点位置坐标为:
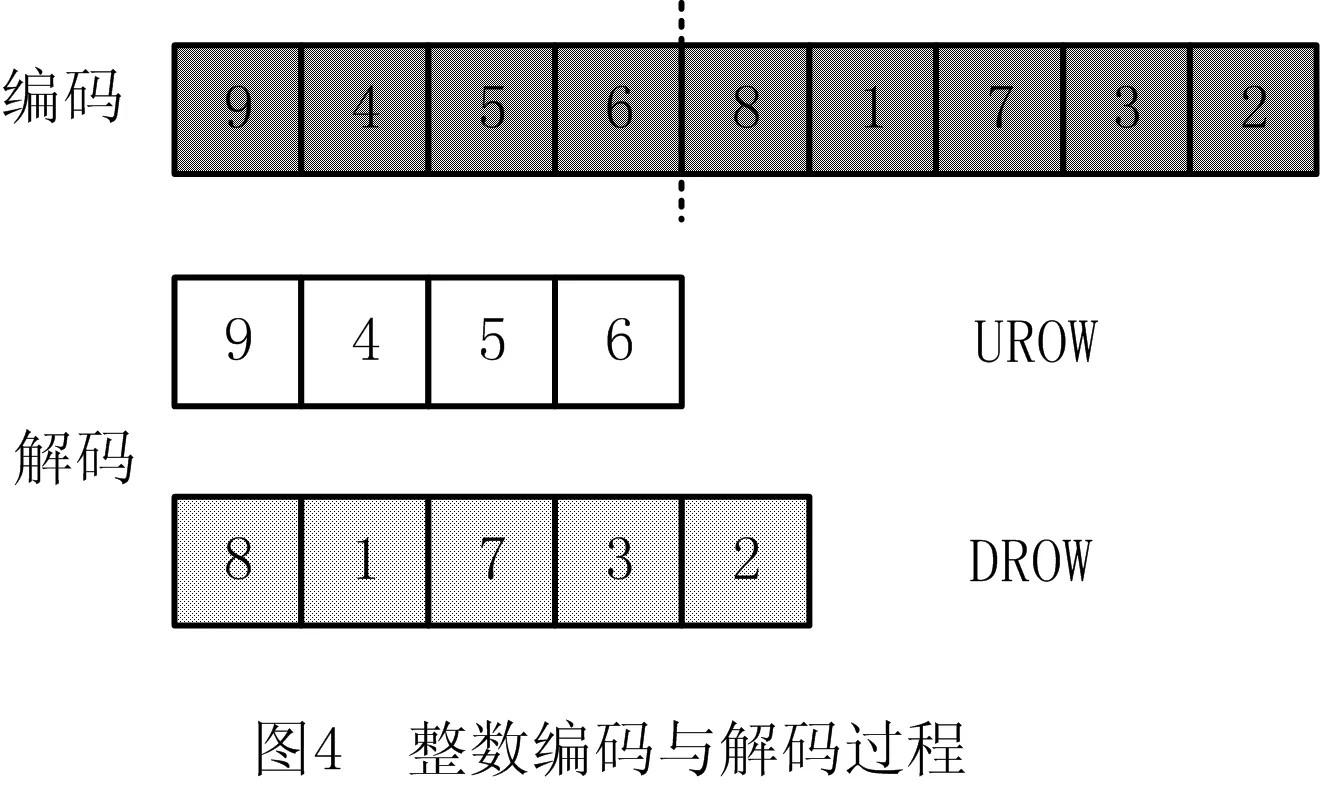
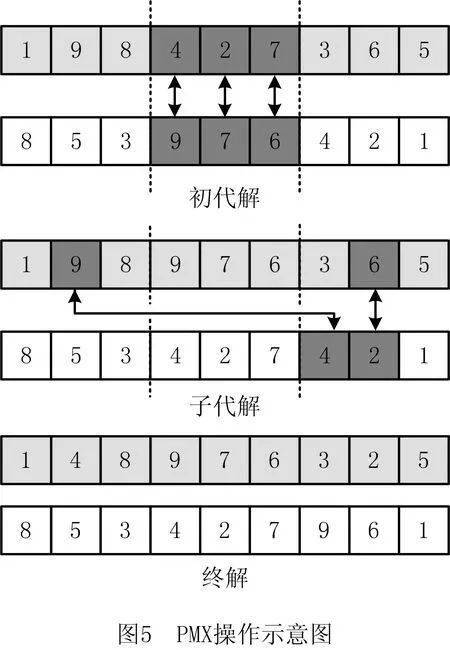
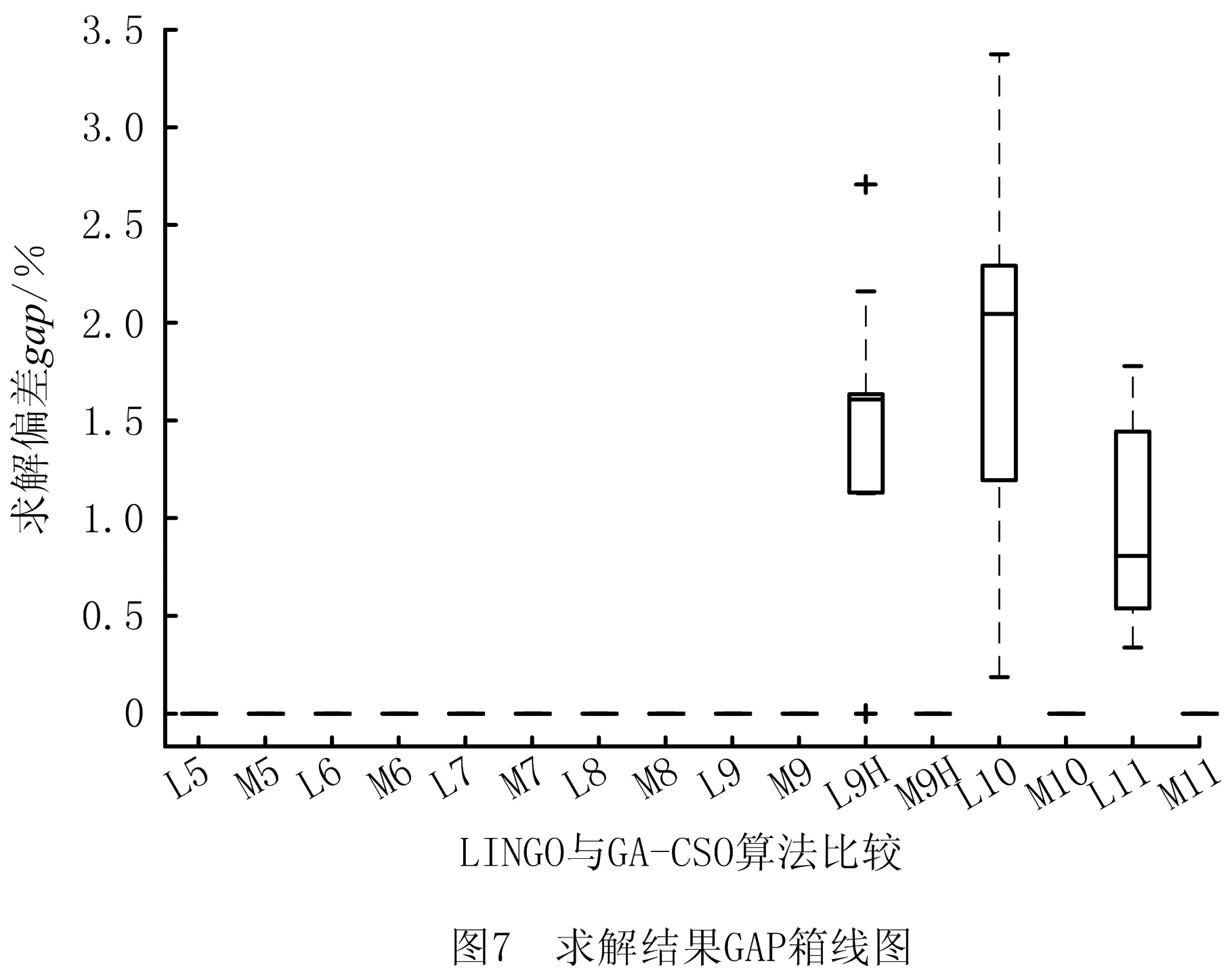
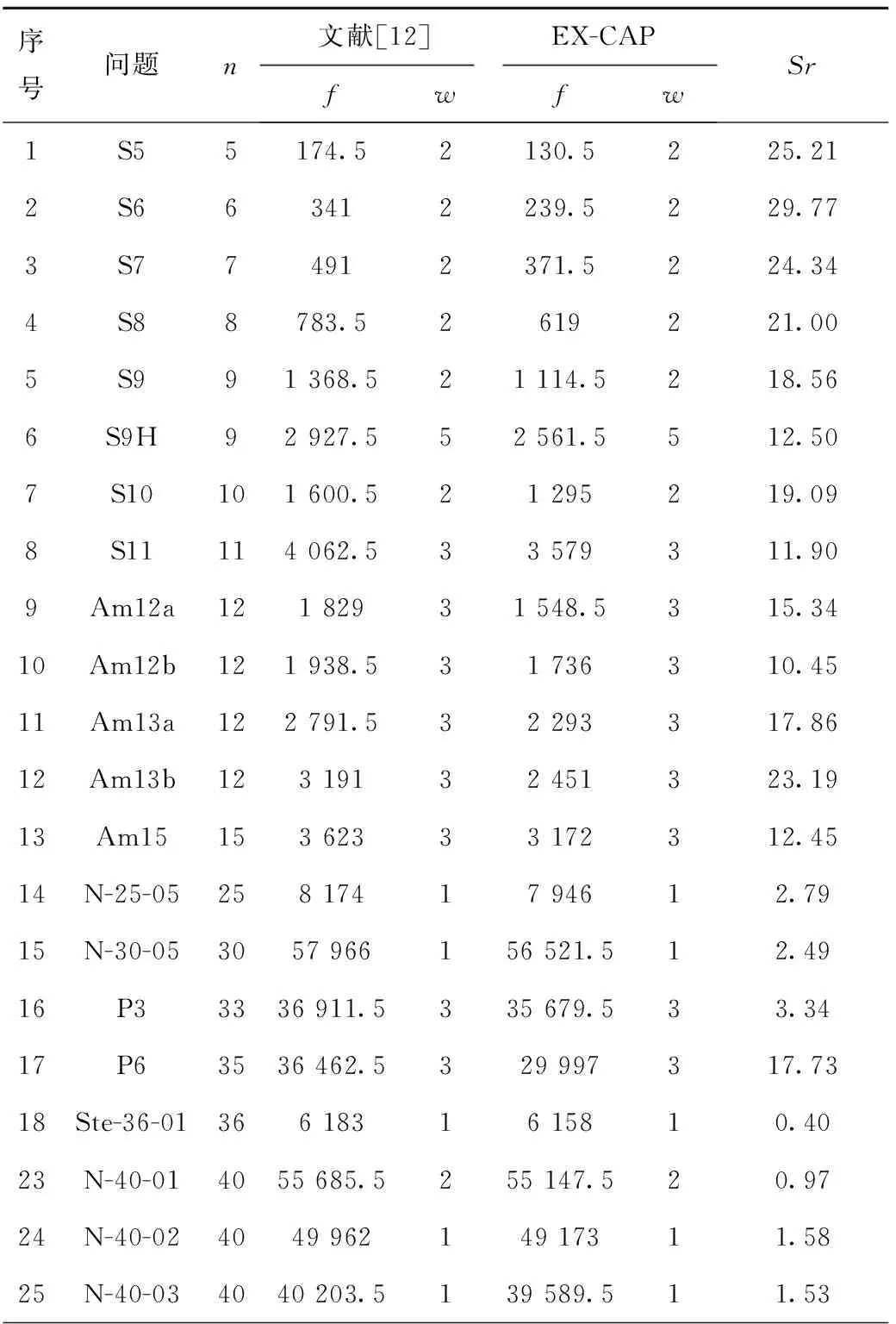
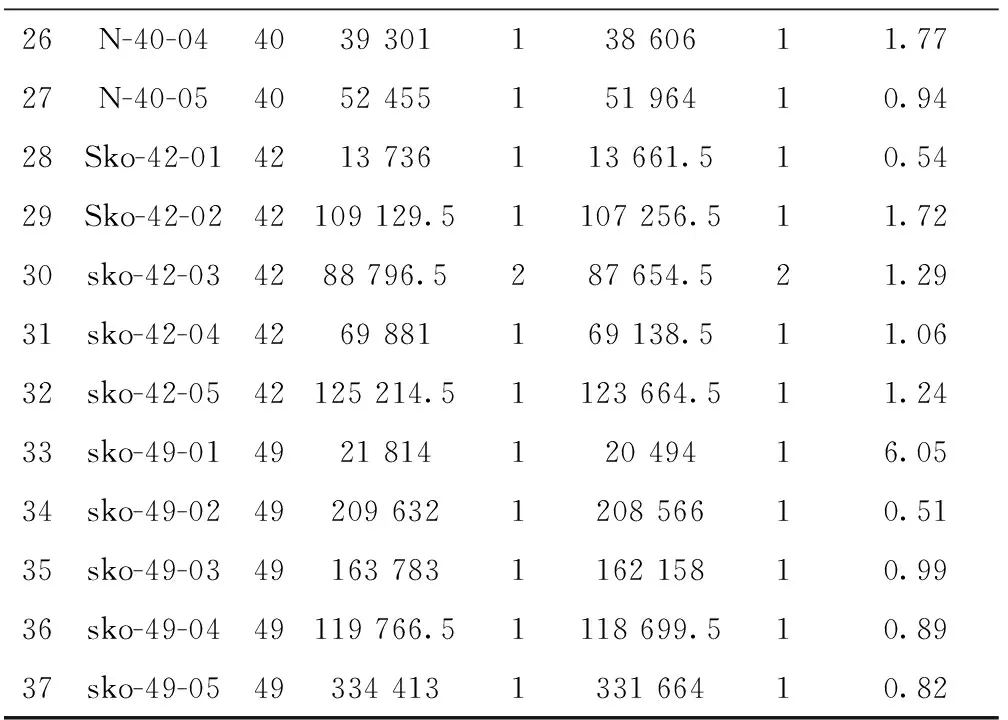
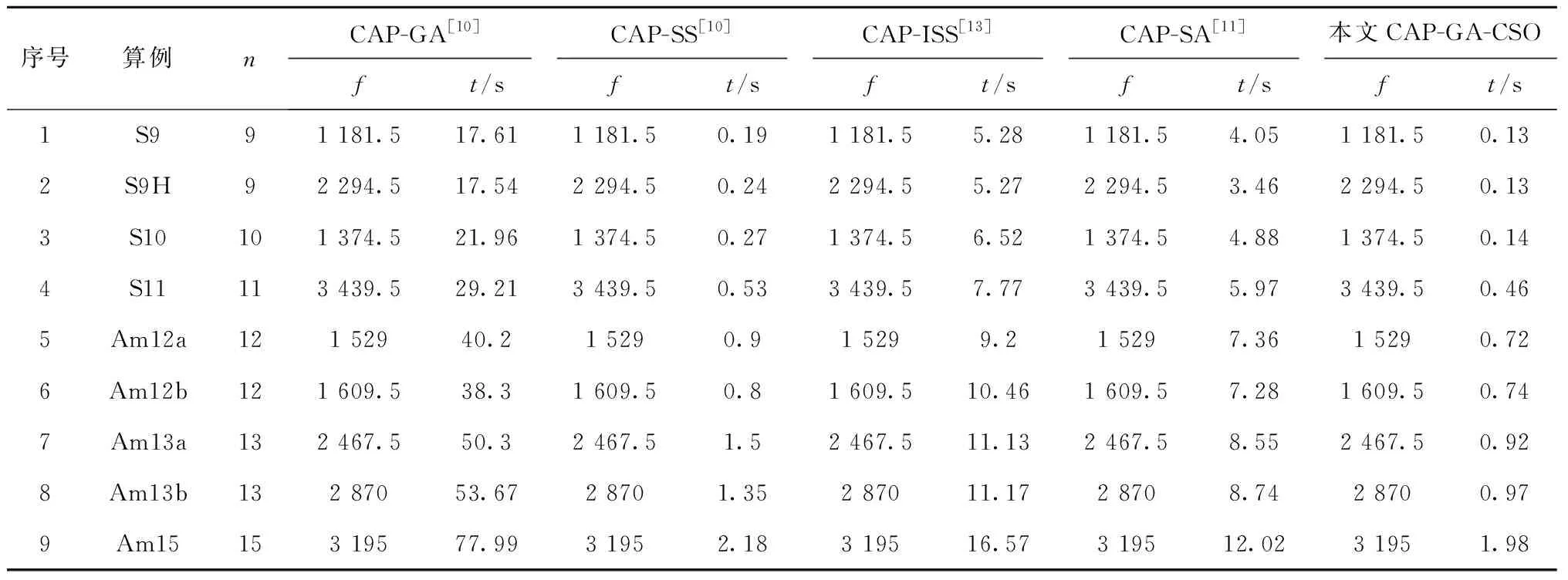
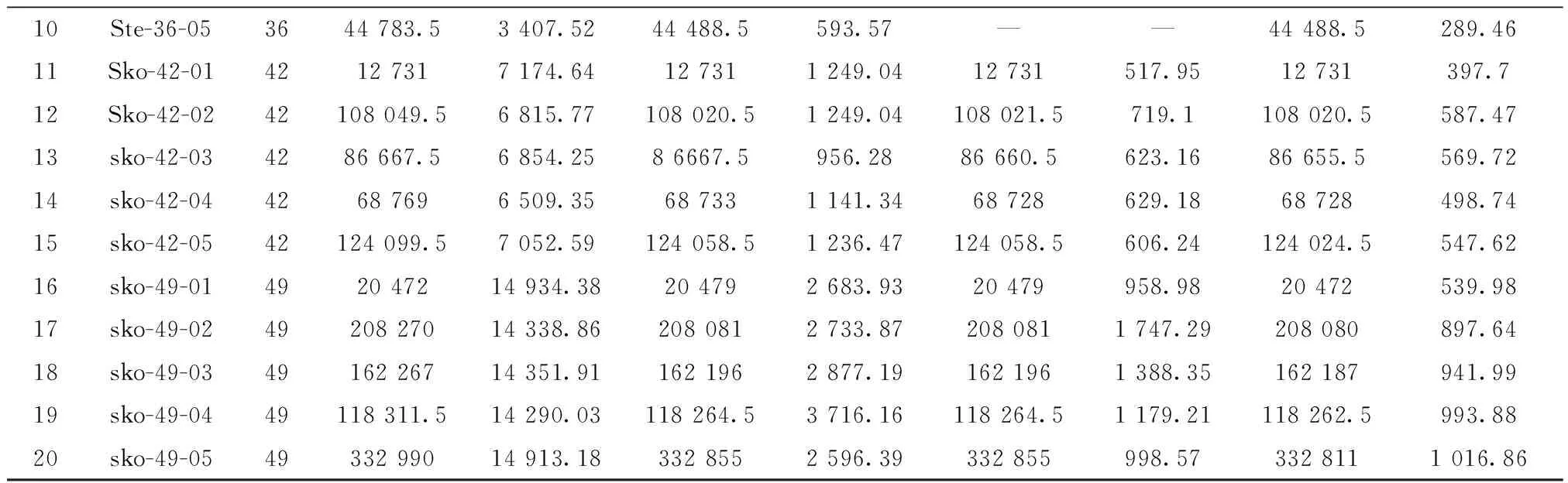
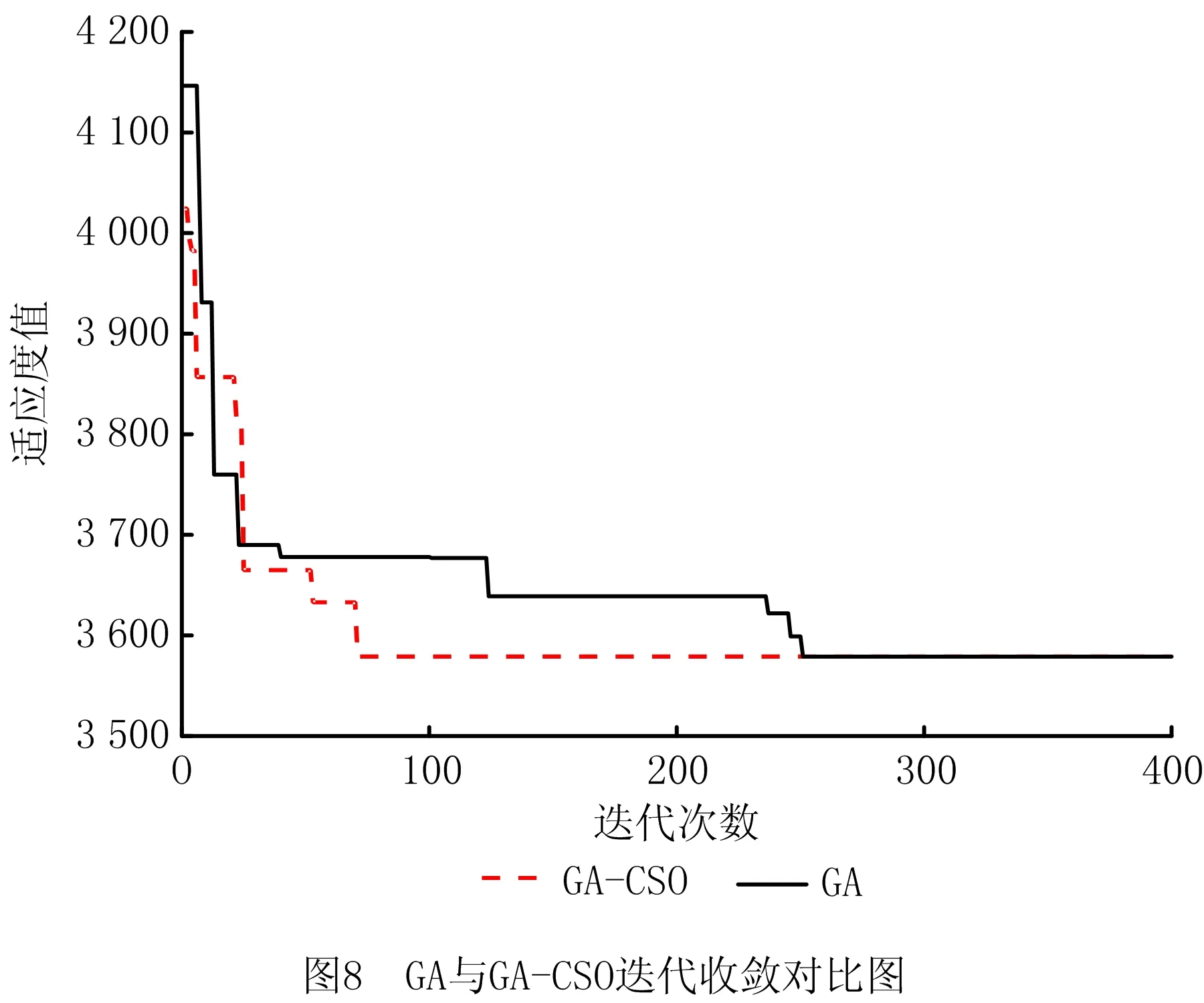
1≤i≤n+1,1≤m (1) 1≤j≤n+1,1≤m (2) 其中:βim表示i设施放置在m或者N位置上,若放置在该位置上则βim=1,否则βim=0;βiN,βjm,βjN同理;N为第二行末端设施位置。 结合上述含有未统一物流交互点的约束条件,构造扩展过道布置问题模型(EX-CAP): (3) 1≤i (4) 1≤i (5) 1≤i (6) -αij+αik+αjk-αji+αki+αkj<0, i,j,k∈I,i (7) -αij+αik-αjk+αji-αki+αkj≤1, i,j,k∈I,i (8) αij+αik+αjk+αji+αki+αkj≥1, 1≤i (9) βim+βiN≤1,1≤i≤N,1≤m (10) βjm+βjN≤1,1≤j≤N,1≤m (11) βim+βjm≤1,1≤i,j≤N,1≤m (12) βiN+βjN≤1,1≤i,j≤N,1≤m (13) qij=αij+αji,1≤i,j≤n+1,i≠j; (14) αij∈{0,1},1 (15) qij∈{0,1},1 (16) βim∈{0,1},1≤i≤N,1≤m (17) 其中:目标函数(3)表示总物流成本最小化。约束(4)和约束(5)用于计算各物流交互带点之间在水平轴方向上的最小距离;约束(6)预防了同行的设施布置重叠情况的出现;约束(7)~约束(13)确定决策变量,其中约束(10)~约束(13)相互约束,设施i有且仅有一个位置可以放置,同时有且仅有一个设施放置在m处,设施j以及N位置同理;约束(14)验证设施i和j是否所在同一行;约束(15)~约束(17)定义决策变量的定义域。 鸡群算法(CSO)是一种通过模拟生物种群来解决实际优化问题的仿生学算法,该算法的优化方式从鸡群中的等级制度和行为习惯衍生而来,主要体现在角色划分、等级制度的建立以及按照等级制度派生出的随从行为、学习行为和觅食行为等行为规律,通过鸡群中的一系列制度和行为作出如下假设: (1)等级制度 在鸡群中有公鸡、母鸡和小鸡顺序排列的几种角色存在,该序列将个体的适应度值作为划分依据,适应度值排在前列的若干个体身份设定为公鸡,排在中间的个体设定为母鸡,最后的设定为小鸡。同时,将鸡群分为若干个子种群,每个子种群中均有一只公鸡作为代表,带领若干只母鸡和小鸡。在等级制度下,一个子种群内的组间调配关系和组内母子关系将保持不变,这种状态每隔G代更新一次。 (2)行为规律 在鸡群中,具有良好适应度值的公鸡占主导地位,具有良好的支配权,且先于其他个体寻得食物。子群中每个个体均会围绕公鸡进行行动,并假设母鸡或小鸡具有偷取其他个体已经发现的食物的能力,母鸡围绕公鸡进行觅食,小鸡围绕母鸡觅食。 在当前应用的CSO算法中,鸡群中每个个体都对应优化问题的一个解。基本CSO算法分别对公鸡母鸡和小鸡位置更新定义各自的公式,在求解连续性问题上具有较高的求解效率,其寻优过程如图3所示。 基本CSO算法的伪代码如下: Initialization parameter Begin Calculate the fitness value for each individual for T=1:Tmax If mod(T,G)==1 Redefining the intra-and Inter-grouprelationships of Rooster Hens endif Update Rooster location Update hen location Update Chicken location endfor end 2.2.1 初始鸡群产生方法 针对设施布局中的过道布置问题具有组合优化的特性,采用基于设施编码序列的整数编码方式定义个体位置,每只个体的位置X用一个序列来表示,且根据鸡群中所需定位的维度来确定序列的长度,在X中每一维数字表示相应设施的编号,序列中编号的最大值不超过最大维度。 X={x1,x2,x3,…,xi,…,xn}, 1 式中i为设施索引,且i的范围不超过最大维度。每种排布序列代表鸡群中某一个体,同时也代表一种布局方案。以经典n=9的经典算例为例,假定其中某一可行解的序列为x=[9 4 5 6 8 1 7 3 2],若给定第一行设施数目为4个设施,则可行解被划分为两个序列为[9 4 5 6]和[8 1 7 3 2],该序列的整数编码与解码过程如图4所示。 2.2.2 GA-CSO算法的离散化设计 (1)离散化设计 传统的遗传算法(Genetic Algorithm, GA)是根据生物进化的特征和遗传学机理为原理进行的设计,是一种通过自然进化等方式随机搜索适应度值的方法,其优点在于可以直接面向对象进行寻优,不会受到连续函数或微分形式的约束和限制,可以极大程度地简化编码与解码形式,同时GA具有一定的自适应性,通常GA以群体中个体为对象,并采用随机搜索方式作用在已编码的参数空间内,使其打开搜索进程。GA主要的算子包括选择、交叉和变异等,其中交叉操作是作为GA算法的重要特征性操作,同时也是离散化设计与保持种群中个体多样性的重要操作。 传统鸡群算法应用公式计算公鸡、母鸡与小鸡的觅食位置,很难适用于离散化问题。针对该问题,提出采用遗传算法中的交叉操作算子与之混合的方式对公鸡、母鸡和小鸡的位置进行更新,其中公鸡个体采用同一等级内进行交叉操作,母鸡则根据行为与同组内的公鸡进行交叉操作,其中交叉操作采用部分映射交叉(Partially-Mapped Crossover,PMX),具体操作如图5所示。 (2)定向化策略 基本CSO算法,小鸡只向母鸡妈妈学习,这便限制了小鸡的学习方式,且无法保证小鸡一定是向更好的方向进行位置更新。但在自然界中,小鸡的学习方式更为多样化,同时由于追随母鸡妈妈的缘故,小鸡容易随同组的母鸡妈妈一起陷入局部最优,因此采用定向策略与离散化策略将小鸡个体的交叉对象由原有的母鸡妈妈更换成当前在种群中地位最高、适应性更强的个体,这样小鸡个体在更新后仍具备良好的寻优方向且易于跳出局部最优。 2.2.3 变异算子与终止准则 在上述局部搜索阶段,对鸡群中的公鸡、母鸡和小鸡分别进行了离散化设计,在离散化设计的基础上,对其进行变异操作,其变异方式采用多点变异操作。在变异的过程中,设置变异概率Pm并比较随机值R与Pm的大小,当Pm>R时,发生变异,通过变异操作不断地扩大搜索广度,不断更新当前最优解。同时为了提高GA-CSO算法的求解效率,与遗传算法等求解CAP算法进行比较,本文采用以最大迭代次数Tmax作为终止条件,Tmax的取值根据问题求解规模n及最优值的稳定程度而定,设置T为鸡群更新次数的计数器,若T>Tmax,则算法终止,返回当前最优值fitbest。 上述离散鸡群算法步骤如下: 步骤1初始化种群并定义相关参数:鸡群数量N,鸡群等级占比rPercent、hPercent、mPercent,设施规模(维度)n,群内更新代数G,交叉概率Pc,变异概率Pm。 步骤2产生初始种群表Chrom,计算鸡群适应度值并建立适应度表fitness,比较并挑选当前最优适应度值fitbest和全局最优序列(布置方案)Xbest,将适应度值排序,按照鸡群内等级占比划分为公鸡、母鸡、小鸡和母鸡妈妈以及确定种群内分组。 步骤3进入迭代,令T=1。 步骤4建立新种群表newChrom与新适应度表newfitness。 步骤5如果T%G=1(取余数),重新建立鸡群等级制度,对鸡群的等级制度和组内关系进行更新。 步骤6令i=1:rNum,开始公鸡位置更新循环,生成i以外的另一只公鸡anotherooster。 步骤7两只公鸡进行交叉变异,将得到的第i只公鸡放入,表中其原来对应位置。 步骤8令j=(rNum+1):(rNum+hNum),开始母鸡位置更新循环。 步骤9根据鸡群内部等级制度与组内关系,确定母鸡在组内所对应的公鸡roosterj,并将第j只新母鸡hensj与roosterj进行交叉变异,将得到的第j只母鸡放入表中其原来对应位置。 步骤10令k=(rNum+hNum+1):N,开始小鸡的循环。 步骤11根据鸡群内部等级制度与组内关系,确定小鸡所在种群中母鸡最优位置以及母鸡序列,将小鸡与其进行交叉、变异,得到的小鸡序列放入表中其原来对应位置。 步骤12计算新表newfitness中的适应度值。 步骤13比较并挑选当前产生的最优适应度值newfitbest,若newfitbest 步骤14令T=T+1。 步骤15比较T≤Tmax,继续执行步骤5~步骤14,否则输出全局最优值fitbest以及所对应的最优位置序列。 算法流程如图6所示。 为验证所提模型的正确性,采用LINGO优化器对上述所构建模型进行不同规模的算例求解。本文实验所采用的计算机硬件配置为Intel(R)酷睿i5-8400、主频2.8 GHz、内存8 GB,Windows10操作系统。除应用LINGO优化器对所提问题进行小规模算例验证外,为了验证所提混合鸡群算法(GA-CSO)的求解性能,应用MATLAB R2016b进行计算求解。本文分别应用GA-CSO对初始CAP问题的9~49不同规模进行计算并将结果与文献[9]的遗传算法、分散搜索算法、文献[10]的模拟退火以及文献[12]的改进分散搜索算法进行对比,经过大量算例测试和程序调试后确定的参数设置如表1所示。此外,兼顾求解效率与质量,在大量数据测算后总结得出Nu∈[T1,T2],其中T1=floor(n/2)-2,T2=floor(n/2)。为了更好地说明情况并保证所使用的数据具有一定准确性,对每种算例均进行至少10次的运算。 表1 算法参数设置 续表1 因符合问题特征的MIP数学模型中含有非线性约束条件,致使LINGO优化器求解过程中无法在较为合理的时间内对大规模算例进行高效求解。通过表2可得:10规模算例已经无法在合理时间内求解出最优解,因此在原有小规模S9算例基础上,提取S9中5到8规模数据进行求解计算,针对大于11规模的测试问题,将其运算时间设置在1 800 s,若无法求得计算结果则用“-”表示。 表2 LINGO精确解与GA-CSO算法的计算结果 续表2 此外,结合表2的求解结果,计算LINGO与GA-CSO的求解偏差gap,绘制箱线图(如图7),该图主要显示出6个数据的节点,可以很好地反映原始数据分布的特征以及离散情况。图7中上下线框、中间线、点画线分别表示一组数据的上下四分位、中位值、平均值,此外上下框线的边缘线表示最值到四分位数的取值区间,上下四分位、中位值、平均值。从图7中可以看出,对于GA-CSO所计算的小规模问题,其偏差基本为0,而在求解S9H、S10、S11问题时,其求解偏差为:1.34、1.82、0.95,由此可得GA-CSO具有较为良好的求解性能。 物流交互点的变动致使总物流成本也发生变动,因此对不同因素下的CAP问题数学模型求解结果进行对比(如表3),并计算其节约率Sr。对比发现:所提出的EX-CAP问题的物流成本均小于仅考虑考虑通道宽度及总流量入口CAP问题的物流成本,且最高降低29.77%,可以看出所提出的EX-CAP问题在一定程度上可以为实际生产布局提供部分理论指导。 表3 考虑不同因素的CAP问题模型求解对比 续表3 为验证改进鸡群算法在求解过道布置一类问题的有效性和普适性,除对所提问题进行求解验证外,对设施数小于等于15规模的算例进行测试,采用混合鸡群算法求解初始过道布置问题,每个测试问题采用10次计算取其平均值的方式以增强数据的说服力度,将所得结果与CAP-GA、CAP-SS、CAP ISS和CAP SA作比较,小规模CAP各算法测试结果、对比数据如表4所示。经表4分析可知,几种算法均可以在较短的时间内寻得最优值,但本文所提的GA-CSO在求解效率上更胜一筹。 表4 求解小规模初始CAP问题的各算法计算结果对比 在对小规模算例进行计算验证后,为了可以更进一步说明算法的高效性,应用GA-CSO对大CAP原初始问题的大中规模算例进行求解计算,要求对每种算例进行不少于10次计算,计算结果及时间均取其平均值,详细参数参考表1中的参数设置,将所计算出的结果与Ghosn等[10]的SS算法、GA算法以及毛丽丽等[13]的ISS算法所求结果进行对比,结果如表5所示。 表5 GA-CSO求解大规模原始CAP问题计算结果 续表5 由表5可知,随着规模的增大,求解时间与问题规模成正相关关系。在求解质量方面,除测试问题sko-49-01外,GA-CSO明显优于传统GA,对于sko-49-01测试问题求解质量相同的情况下,GA-CSO的求解结果在相同问题规模下明显优于GA。不难看出,随着问题的规模增大,SS与GA运算时间随着问题规模的增大也大幅度地增加;而GA-CSO与ISS相比,随着规模的增大,各项指标均可以平缓增长。 此外,根据计算得到的结果,选定S11算例为基础数据,绘制如图8所示的迭代收敛图,为了对比结果明显,选用所含参数类别大致相同的GA与其作参照,并将GA设置与GA-CSO相同的算法参数。由图8可以看出,当两种算法均可以在有限的迭代次数内迭代到相对最优值时,GA-CSO算法在迭代至71次时趋于平稳状态,而GA则在迭代到251次时趋于稳定,且在时间方面GA-CSO明显优于GA。因此可以得出结论:GA-CSO在求解质量和效率方面都有相对较好的性能。 本文结合实际生产情况,考虑了物流交互点在过道边线水平方向上的变动对过道布置以及总成本的影响,并构建了目标函数为最小化物流成本的EX-CAP数学模型,提出一种混合遗传操作的新型鸡群算法对该问题进行求解。通过应用LINGO优化器所求精确解并与其他算法进行对比验证,总结本文主要成果如下: (1)构建了EX-CAP混合整数非线性规划模型,并用LINGO11软件对该模型的小规模问题进行了精确求解,验证了所构建的MIP数学模型的合理性。 (2)将基本CSO与GA结合,进行离散化设计,采用部分映射交叉算子(PMX)对解序列进行交叉操作。同时,对于种群中适应度值较为落后的个体采用定向化策略使其在一定意义上朝着最优解方向进化。 (3)为了验证所提算法的性能,应用其计算求解原CAP问题,并与文献[10-11,13]等一系列算法求解结果进行对比,结果表明:GA-CSO具有操作简单、收敛速度快的优点,且其内部的GA中交叉、变异操作以及定向化策略帮助其克服了陷入局部最优的难题,具有较好的求解精度和求解效率。 本文所提EX-CAP模型在一定程度上较为贴合实际,但其物料搬运位置仍然不够灵活。为了更贴近实际生产情况,下一步将设施的物料搬运点位置从固定在靠近通道边线中点处改进成在一定范围内设置进行研究。1.3 EX-CAP模型
2 求解EX-CAP的GA-CSO算法
2.1 基本鸡群算法

2.2 基于遗传的混合鸡群算法(GA-CSO)
2.3 混合鸡群算法流程
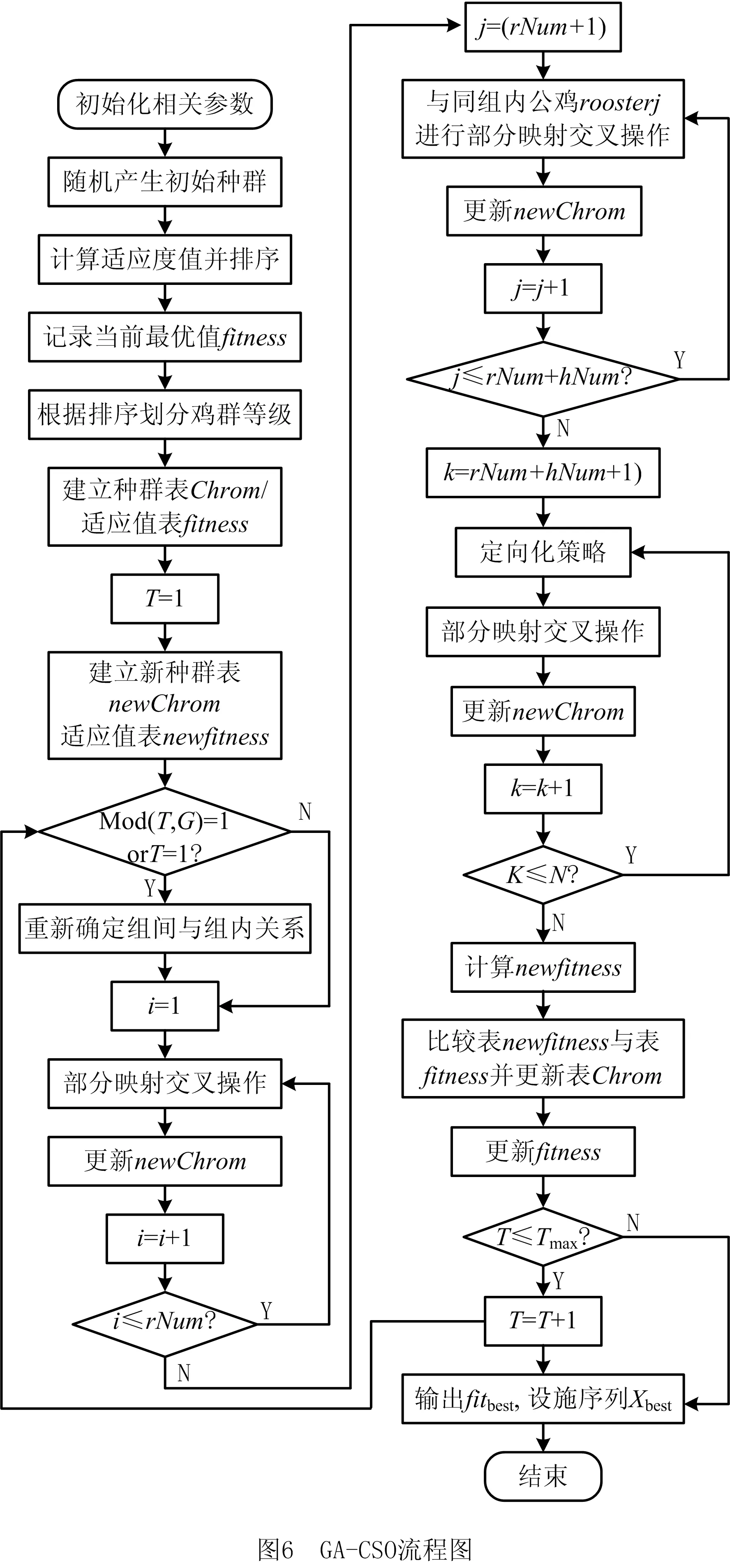
3 实验结果与分析
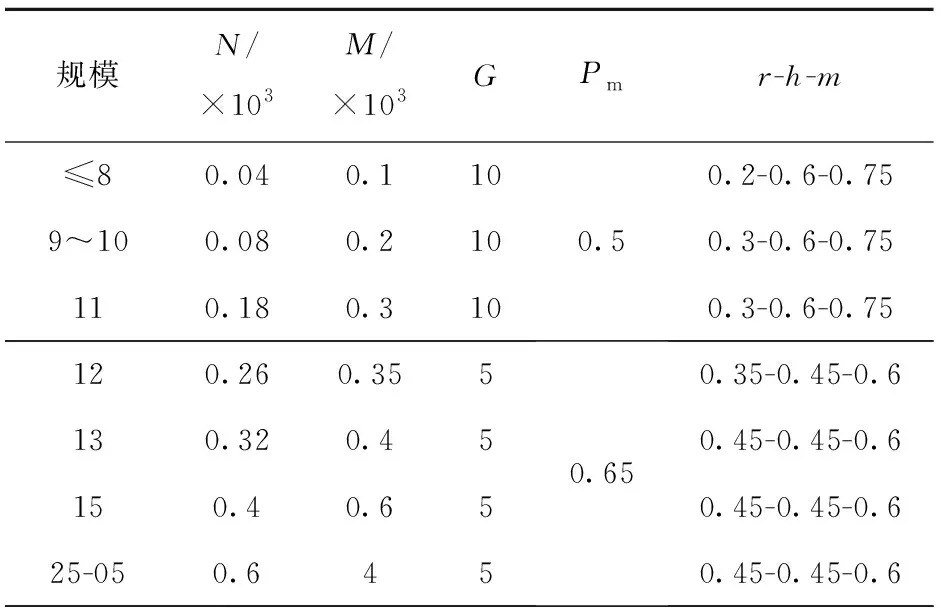

3.1 EX-CAP模型的验证
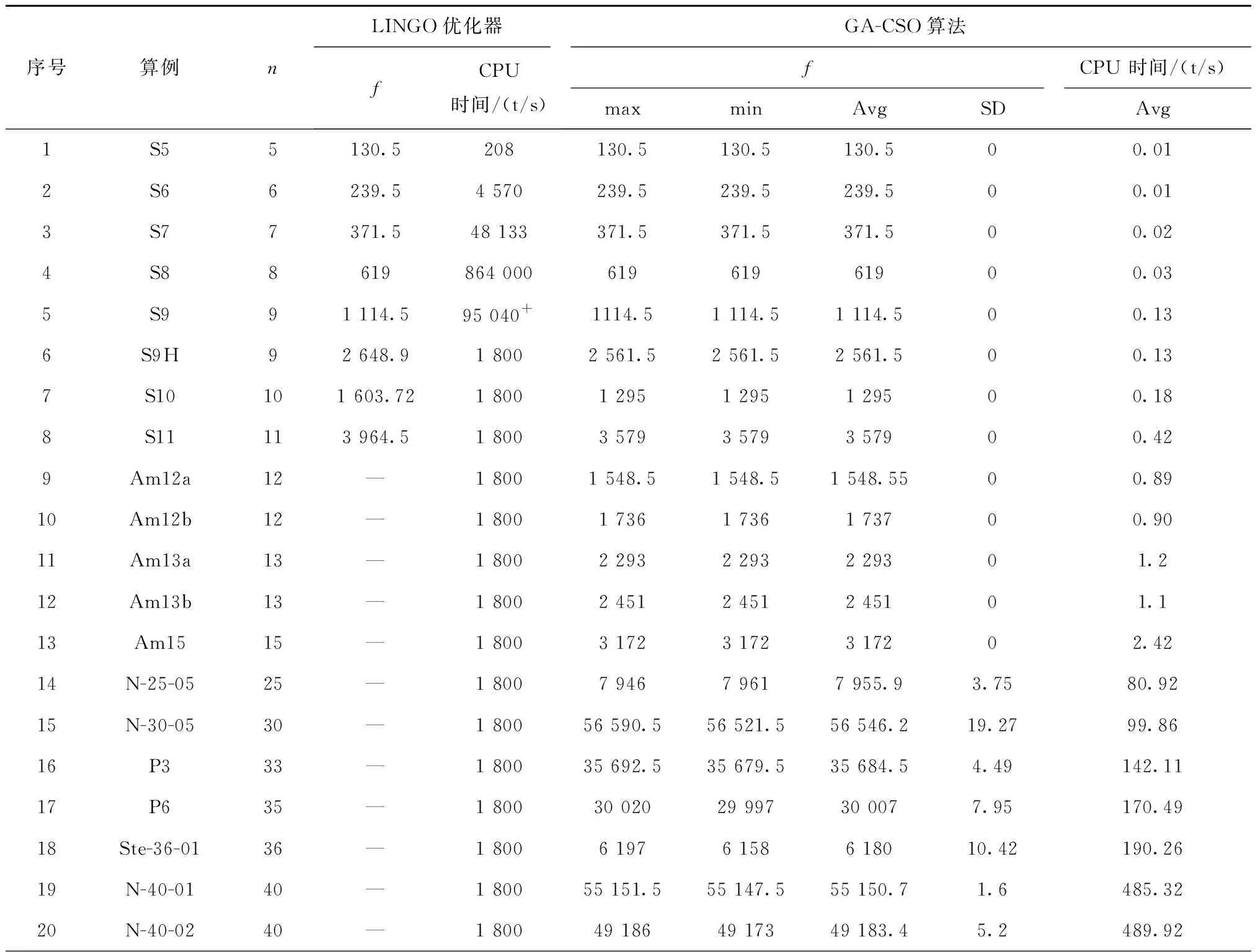
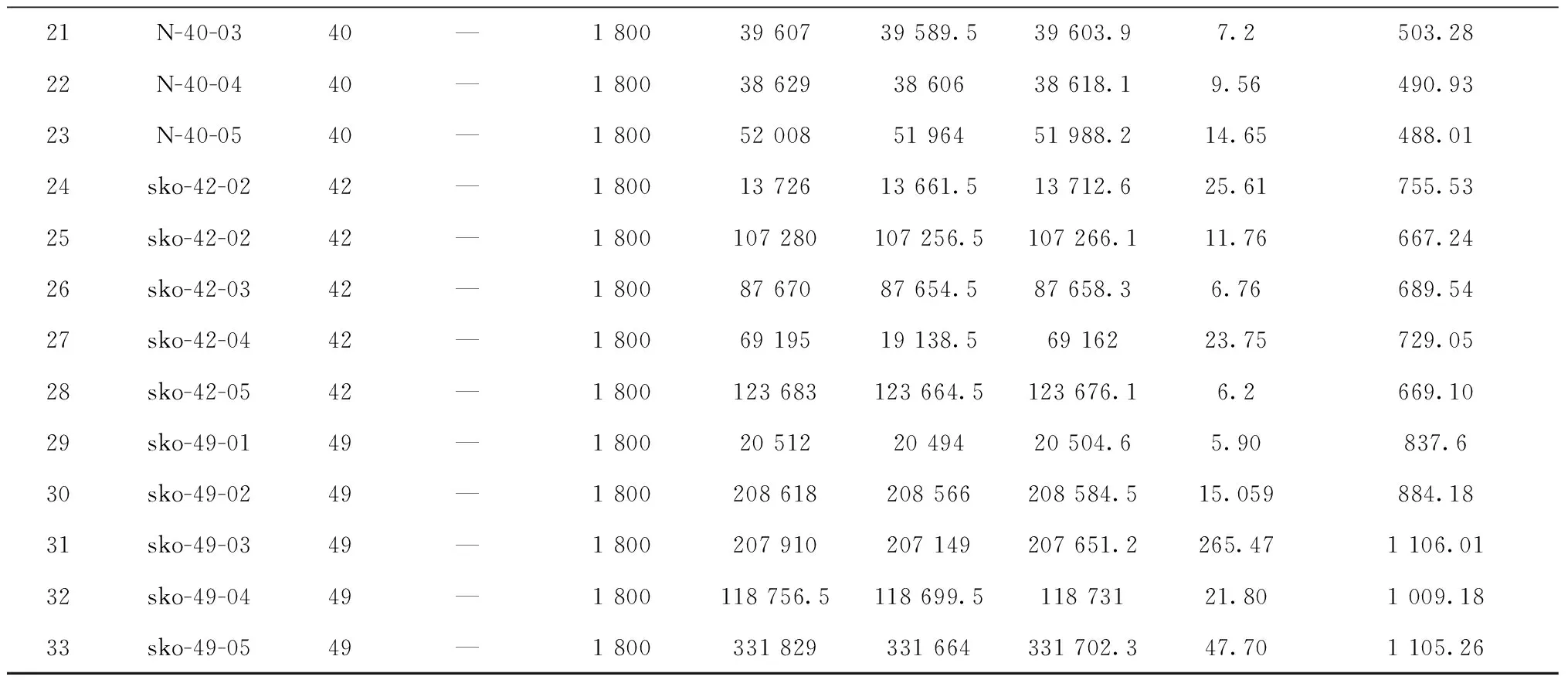
3.2 算法验证

4 结束语

