研究方案设计影响区域水环境库兹涅茨曲线形状*

丁 月，王伟民，田琳静，王子康，高 静，许新瑶，董 雪，蒲 晓

（首都师范大学资源环境与旅游学院，北京 100048）

0 引 言

随着人口增长和社会经济的快速发展，水环境保护的压力日益突出.未来潜在的经济规模扩大对我国水生态环境可能形成更大压力，尽管我国水污染防治措施日趋完善，但区域水环境保护形势依旧严峻［1］，水环境恶化已经成为当前制约经济增长的重要因素，探究水环境污染与经济增长的关系对于维护区域可持续发展具有重要的科学意义［2］.研究水环境质量和经济发展的相互关系，也能够为通过经济发展状况推测水环境质量提供可能，有利于快速推断大区域范围内的水环境质量变化状况.已有研究证实区域水环境质量与经济发展的关系可能符合环境库兹涅茨曲线（environmental Kuznets curve，EKC）［2］.EKC 描述的是，环境污染程度在经济发展初期会随经济增长而加重，当经济发展到一定水平时，环境污染程度达到最大，而后环境污染程度随着经济发展而下降，即环境污染与经济发展之间的变化趋势呈现倒U形的曲线关系［3-4］.然而，水环境质量与经济发展的关系在不同研究中结论并不一致，EKC呈现不同形状，如：在环太湖经济圈经济增长与水环境质量关系的研究中，人均国内生产总值（人均 GDP）与高锰酸盐指数（CODMn）、总氮（TN）之间的EKC呈现倒N形，人均GDP与总磷（TP）之间的EKC则呈现线形［5］；使用相同指标但在不同地区的研究结果也有差异，人均GDP与工业废水排放量的EKC在黑龙江省呈现倒N形［6］，在南京市呈现 U 形［7］，在济南市和天津市呈现 N 形［8-9］，在湖南省则无明显关系［10］.通过综合分析，每个案例的方案设计都包含研究区范围、研究时长、水环境指标和回归方法4个方面：研究区范围主要是指研究区域的尺度，如省、市等；研究时长指选取的时间范围，如5或10 a或者其他时长；水环境指标包括污染物的浓度和废水的排放量等；回归方法包括二次或三次多项式模型等.以上因素可能对研究结果有一定影响.本研究通过对已公开发表的文献进行整理与分析，关注可能影响EKC形状的相关因素，建立EKC形状与关键影响因素之间的函数关系，旨在分析研究方案的设计对区域水环境库兹涅茨曲线形状的影响，为区域水环境质量与经济发展EKC关系研究提供参考.

1 数据与方法

1.1 数据描述

本研究筛选了2000—2017年公开发表的有关水环境质量与经济发展的实证研究论文，筛选标准包括：环境质量指标中涉及水环境相关指标；经济发展指标为人均GDP；研究区域范围尺度较为明确；研究水环境状况与经济发展的EKC形状.经过筛选，最终获得符合标准的有效文献52篇，共包含116个案例，案例数量根据文献研究区的数量进行认定，如在1篇题为“苏、锡、常经济增长与水环境污染的关系——基于ARDL和ECM的实证分析”的文献中，分别对苏州、无锡和常州3个区域的水环境质量与经济发展的EKC关系进行了研究，即有3个案例.

1.2 文献数据特征

根据研究区范围、研究时长、水环境指标和回归方法4个设计方案的分级分类设置的案例数量见表1.研究区域范围差异明显，通过梳理文献中案例，将研究区域划分为市、城市群、省和区域4个等级，多数案例选择的研究区范围尺度为市；研究时长范围为 6～33 a，将其划分为≤10、11～15、16～20和＞20 a这4个等级，在案例中，研究时长多集中在11～15 a；案例中水环境质量指标涉及较多，包括CODMn、TN、TP、氨氮（NH3-N）、生化需氧量（BOD5）、叶绿素a（Chla）、重金属、污水排放量、工业废水排放量、农业废水排放量、农业面源污染、化学需氧量（COD）、农药使用量和化肥施用量等，根据指标类型将其分为污染物浓度、废水排放量和污染物排放量3类，CODMn、TN和TP含量等归为污染物浓度类指标，各类废水排放量归为废水排放量类指标，COD排放量以及化肥施用量等归为污染物排放量类指标，多数案例选择废水排放量指标作为水环境污染指标，选用最少的指标为污染物排放量指标；回归方法分为二次多项式模型、三次多项式模型和其他模型3类，多数案例使用三次多项式模型.

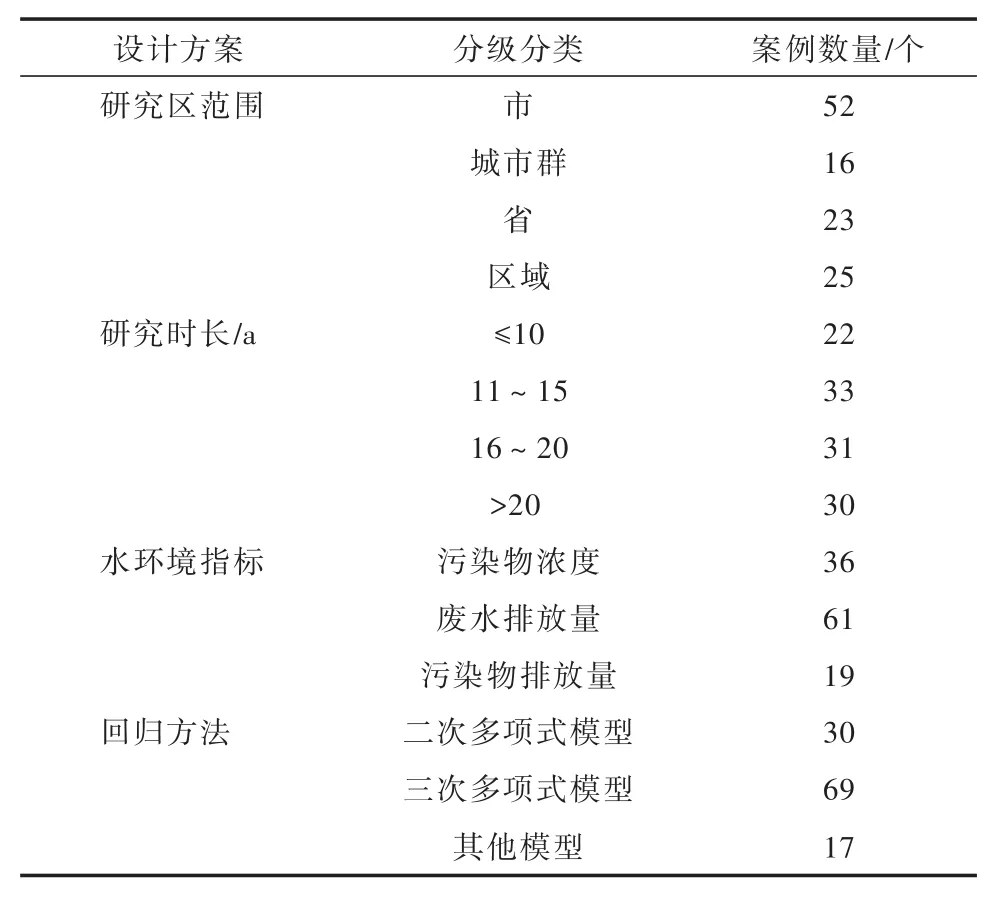
表1 4个设计方案的案例数量分布情况

在116个案例中，EKC形状差异较大，可划分为U形、倒U形、N形、倒N形、线形和其他形（无明显形状）6种.大多数研究的EKC形状呈现倒U形，案例数占案例总数的30.2%；其他形的案例数也较多，占案例总数的24.1%；呈现为线形的案例数最少，具体曲线形状分类状况如表2所示.可见水环境质量与经济发展EKC形状并不总是呈现倒U形.

表2 环境库兹涅茨曲线（EKC）形状分类状况

1.3 数据分析

选用logistic回归方法探讨研究区范围、研究时长、水环境指标和回归方法对EKC形状的作用和贡献；通过贝叶斯判别分析方法建立并通过关键因子推断EKC形状的判别函数，进一步判断关键因子对EKC形状的影响.统计分析过程在IBM SPSS Statistics 25中完成.

1.3.1 Logistic回归分析

水环境质量与经济发展关系的EKC形状可能受研究方案设计的影响，为探讨研究区范围、研究时长、水环境指标和回归方法的影响，将EKC形状设为因变量，根据其形状进行编码（U形、倒U形、N形、倒N形、线形和其他形6种分别编码为1～6）；同时将4个可能影响因素设为自变量，选用多类别logistic回归方法进行分析，探索研究方案设计对EKC曲线形状的作用.

多类别logistic回归是一种概率型非线性多变量回归模型，用以研究多分类观察结果与影响因素之间的关系，可以筛选出对事件发生影响较为显著的因素，并剔除不显著的因素［11］.多类别 logistic回归使用线性预测函数来预测观测数据i的结果为k的概率，函数式为

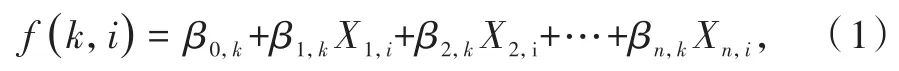
式中 Xn，i表示第 n 个观测变量/特征，βn，k为回归系数，表示第n个观测变量/特征对第k个结果的影响.将β0，k看作 X0，i=1时，可得到式（1）的向量化形式

式中 βk为回归系数向量，表示的是观测数据Xi对结果k的影响度（重要性）.

在进行logistic回归分析时，如遇到多分类无序变量，要进行哑变量处理，哑变量又称虚拟变量，是量化了的质变量，通常取值为0或1，哑变量是对于等级性数据 x，用变量 μ（x，i或 j）表示成关于定性因子（0，1）展开，即关于 μ（x，i或 j）=（μ（x，1），μ（x，2），…，μ（x，m）），其中一个定性变量（m个等级）对应一个向量，一个定性变量就变成可以进行数值运算的数值向量［12］.

1.3.2 判别分析

为探索能否通过关键影响因子状况来判断水环境质量与经济发展关系的EKC形状，本研究针对116个案例，使用由logistic回归分析筛选出的关键指标对EKC形状进行判别分析.

判别分析是多元统计中用于判别样品所属类型的一种统计分析方法，其基本原理是按照一定的判别准则，建立一个或多个判别函数，用研究对象的大量资料确定判别函数中的待定系数，并计算判别指标［13］.判别分析分为距离判别、Fisher判别和贝叶斯判别3类.贝叶斯判别分析可根据样本先验概率计算后验概率，通过最大后验概率划分样本分类，使期望损失达到最小.贝叶斯判别依据样本多元分布的概率密度计算后验概率，能有效降低判错率，因此，本研究采用贝叶斯判别法.

贝叶斯判别法的原理为，设有总体Gi（i=1，2，…，k），其先验概率分别为 q1，q2，…，qi，Gi的概率密度函数为f1（x），f2（x），…，fi（x）［13］，在观测到一个样本x的情况下，可用贝叶斯公式计算其第g（g=1，2，…，k）总体的后验概率为

对于待判样本 x，如果在所有的P（g/x）中，P（h/x）最大，则判定x属于第h总体.通常会以样本频率作为总体先验概率.

通过判别分析建立一个判别函数，并利用此函数对样本所属类别进行判断.判别函数的一般形式为

式中Y为判别指标，Xn为反映研究对象特征的变量，an为各变量的判别系数.

2 结果与讨论

2.1 Logistic回归分析结果

以EKC形状为因变量，以研究区范围、研究时长、水环境指标和回归方法为自变量的logistic回归模型信息显示回归成立（表3）.纳入自变量后，模型-2倍对数似然值（-2 log like lihood，-2LL）较仅常数项时明显降低，显著水平（P）＜0.01，表明模型拟合效果提升，且至少有1个影响因子的偏回归系数不为0.

表3 EKC形状与影响因子logistic回归模型的拟合信息

影响因子对EKC形状作用的显著性通过模型拟合的似然比检验进行判断（见表4）.与仅常数项纳入模型的-2LL（263.580，表 3）相比，4个影响因子分别纳入回归模型后均明显降低，提升了模型拟合效果.根据似然比检验结果，研究时长、水环境指标和回归方法对EKC形状的作用具有显著影响，P分别为0.048、0.015和0.001；而研究区范围对EKC形状的作用不显著，P为0.295.

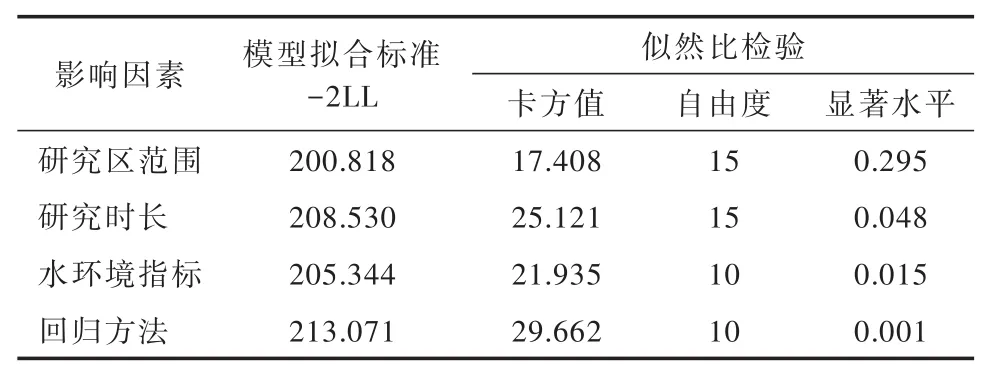
表4 影响因素与EKC形状logistic回归模型的似然比检验

由于本研究的自变量研究区范围、研究时长、水环境指标和回归方法是多分类的无序变量，对这4个影响因素进行了哑变量化，在进行哑变量设置时，一般需要选择一个出现次数较少的分类作为参照.因此，在本研究中分别将自变量研究区范围、研究时长、水环境指标和回归方法中对应的区域、＞20 a、污染物排放量和其他模型作为参照.根据logistic回归模型运行结果的相关参数，可得到EKC形状与关键影响因子的logistic回归方程如下：

式中X1为市，X2为城市群，X3为省，X4为≤10 a，X5为11～15 a，X6为 16～20 a，X7为污染物浓度，X8为废水排放量，X9为二次多项式模型，X10为三次多项式模型；G1～G6分别表示因变量U形、倒U形、N形、倒N形、线形和其他形；P1～P6表示某个案例的EKC形状为U形、倒U形、N形、倒N形、线形和其他形的概率.

2.2 判别分析结果

根据logistic回归结果，研究时长、水环境指标和回归方法是影响区域水环境质量与经济发展之间关系EKC形状的关键因素.为探索上述3种关键因子如何影响EKC形状，采用贝叶斯判别分析法建立不同关键因子状况与特定EKC形状的判别函数.基于贝叶斯判别分析的原理，假设6种EKC形状的先验概率均匀分布.

区域水环境质量与经济发展关系EKC形状与关键影响因子的贝叶斯典型判别函数特征信息如表5所示：判别函数1的方差所占比例为50.4%，说明其可解释样本50.4%的信息；判别函数2的方差所占比例36.2%，解释样本36.2%的信息.二者相加可解释样本85.0%以上的信息，而使用全部5个判别函数可完全解释样本信息.

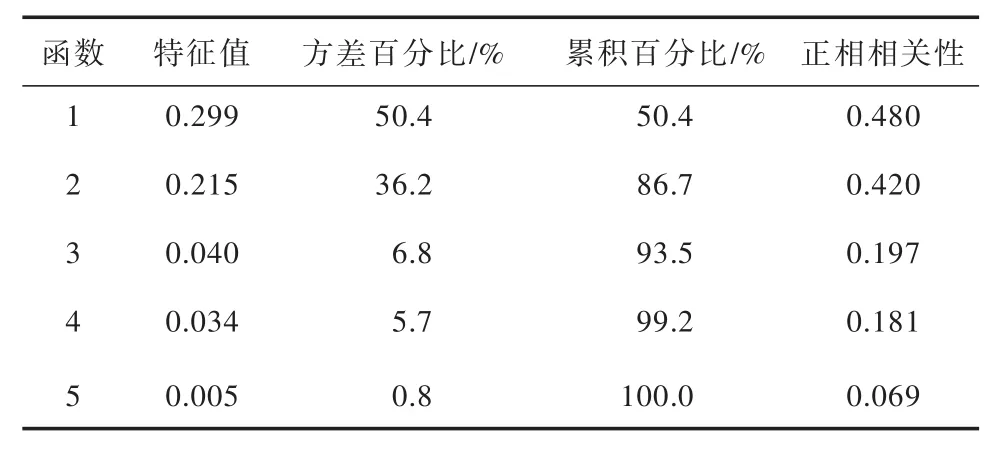
表5 EKC形状判别函数与不同关键因子的特征信息

由EKC形状和关键影响因子判别函数标准化系数结果可判断在各判别函数中影响因子对EKC形状判断的重要性（见表6）.例如：在函数1中，废水排放量被赋予的权重最大；而在函数2中，污染物浓度和二次多项式模型的判别作用最大.

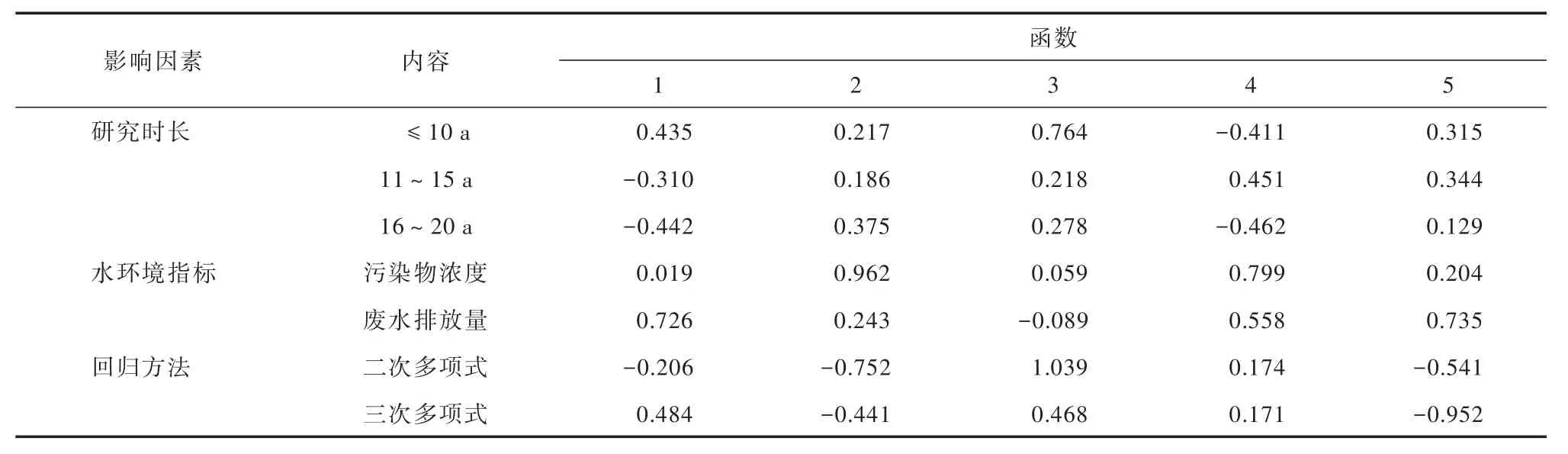
表6 不同EKC形状判别函数与影响因素的数标准化系数

在对新案例进行分类判断时，可通过对分类自变量进行哑变量设置后，将相应值代入判别方程组，所得的最大判别函数值对应的EKC形状即为新案例的判别结果.由贝叶斯判别分析函数得到EKC形状分类判别方程组：

式中 X1、X2和 X3分别表示研究时长（≤10、11～15和16～20 a），X4表示污染物浓度，X5表示废水排放量，X6表示二次多项式模型，X7表示三次多项式模型.Y1、Y2、Y3、Y4、Y5和 Y6分别表示 U 形、倒 U 形、N 形、倒N形、线形和其他形发生的概率.

EKC形状判别结果见表7，表明研究时长、水环境指标和回归方法的不同设定，在一定程度上可以影响EKC形状，通过计算得到判别函数对样本的总体判断正确率为33.6%.

表7 不同EKC形状的判别分类正确率 单位：%

为进一步验证研究时长、水环境指标和回归方法对EKC形状的影响，选取水环境与经济发展的相关研究工作，共8个案例，结果如表8所示［14-19］.由验证结果可得，在 8个案例中，有5个案例的研究结果与判别函数的结果一致，正确率为62.5%，进一步表明研究时长、水环境指标和回归方法对EKC形状的呈现具有重要作用.

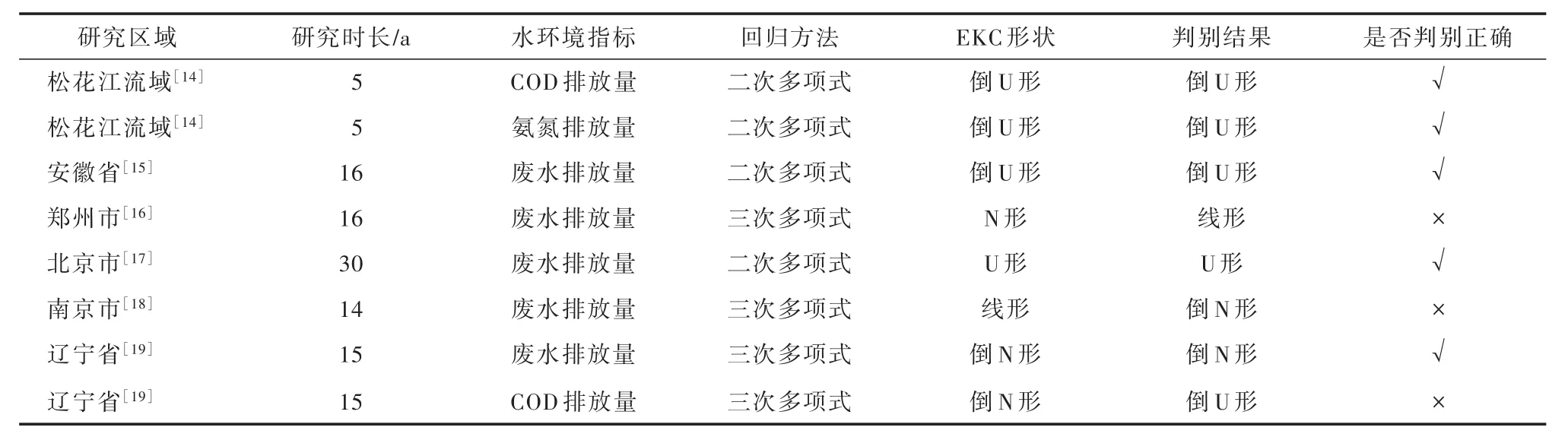
表8 判别函数的适用性验证

3 讨 论

Logistic回归分析结果表明，区域水环境质量与经济发展之间EKC形状与拟合数据的时间跨度（研究时长）、所选取的代表水环境质量状况的指标类型（水环境指标）、采用的数据拟合方法类别（回归方法）有较大关系，而对选取的研究区尺度大小（研究区范围）不敏感.但该回归结果还需进一步验证，因为本研究所选取指标没有涵盖所有对水环境质量与经济发展之间关系EKC形状产生作用的潜在影响因素；另外，对所选取指标的等级划分具有一定主观性，不同的等级划分标准可能产生不同的回归结果.

相关研究表明，区域的经济发展与其经济发展结构与阶段有密切的联系，Markus［20］和 Antonio［21］认为经济的迅速增长使得第二产业比例迅速增加，这使得生态环境问题加剧，当主要经济活动从高污染的工业转向低污染的服务业等产业时，产业的发展对资源环境压力就降低，此时环境污染和经济发展呈现传统的倒U形曲线关系［22］.因此，在研究某一区域水环境与经济发展关系时，应首先明确该区域经济发展结构，以及工业、农业等产业发展所排放的主要污染物种类，选择最具区域代表性的水环境指标；在建立环境指标与经济发展关系时，最简单常见的方程形式是经济收入与环境关系的二次多项式，有的为了突出曲线特征形状而使用经济收入取对数后的二次多项式，得到明显的倒U形曲线，三次多项式则会显示为N形、倒N形等形状.因此，形状与回归方法的相关性较大，在回归方法的选择与运用过程中存在着较大的主观性.

4 结 论

本研究利用logistic回归分析的方法以及判别分析法得到研究方案设计，研究时长、水环境指标、回归方法和研究区范围的选择可影响水环境EKC的形状，这在一定程度上说明，在进行水环境与经济发展的EKC关系的研究时，要考虑研究结论反映的是真实规律还是由研究方案设计的选择而得到的潜在规律.

Logisitic回归分析结果显示研究时长、水环境指标和回归方法对EKC形状具有显著影响，而EKC形状对研究区范围不敏感.使用贝叶斯判别分析方法，选用研究时长、水环境指标和回归方法3个影响因素可实现对EKC形状的初步判断.另外，用于验证的8个案例中有5个案例的结果与判别函数的结果相符，正确率为62.5%，这表明研究时长、水环境指标和回归方法对EKC形状的呈现具有重要作用，即在进行水环境与经济发展的EKC关系研究中，研究方案的设计可以影响EKC形状.本研究结果为水环境质量与经济发展EKC关系研究的数据准备、指标选取和回归方法选择提供了参考，并从侧面反映了EKC曲线的形状主要受水环境指标和回归方法的影响，一定程度上说明了经济增长与水环境污染之间关系的复杂性以及统计上的脆弱性.