Quantum nature of proton transferring across one-dimensional potential fields∗
Cheng Bi(毕成), Quan Chen(陈泉), Wei Li(李伟), and Yong Yang(杨勇),†
1Key Laboratory of Photovoltaic and Energy Conservation Materials,Institute of Solid State Physics,HFIPS,Chinese Academy of Sciences,Hefei 230031,China
2Science Island Branch of Graduate School,University of Science and Technology of China,Hefei 230026,China
3Key Laboratory of Materials Physics,Institute of Solid State Physics,HFIPS,Chinese Academy of Sciences,Hefei 230031,China
Keywords: proton transfer,nuclear quantum effects,atomic resonant tunneling,double barriers
1. Introduction
Proton transfer plays an important role in many fields of physics, chemistry, and biological systems. A typical system is the mixed atomic and molecular phase of solid hydrogen and deuterium.[1]Based on in-situ optical spectroscopy measurements,Howie et al. have investigated the spectral features of the phase IV–III transition and shown that the large differences in the peak widths of the isotopes Raman spectra indicate the presence of proton tunneling in phase IV.[1]Ab initio variable-cell molecular dynamics(MD)simulations have been carried out to study the dynamical properties of phase IV of solid hydrogen and deuterium at high pressures and a temperature range of 300–500 K,[2]aiming to identify the intralayer proton or deuteron transfer and the simultaneous rotation of three-molecule rings in layer II of phase IV. It is found that proton transfer has a direct relation to the unique elongation of molecules in layer II, as well as the lifetime and anharmonic vibrations of the hydrogen molecules.[2]
In biochemistry,the mechanism of proton transfer reveals the light-driven process of biological chromophores. Excited state intramolecular proton transfer is a photochemical process that produces a tautomer with a different electronic structure from the original excited form.[3–8]Using state-of-the-art experimental techniques,such as time-resolved photoelectron imaging measurements, it is possible to see how the addition of a single hydrogen bond and the opening of an excited state proton transfer channel would change the product of a photochemical reaction,and to explore the mechanism of excited state proton transfer process within a single hydrogen bond in simple systems like ammonia dimer.[9]
The proton transfer process in the aqueous-phase reactions has also attracted attention. In a recent study which uses ab initio molecular dynamics to simulate the diffusion of protons between the Brønsted acid site(BAS)and the water molecules in the zeolite pores, it is shown that water clusters of different sizes will greatly affect the competition of proton hopping between the O atoms of BAS sites and within the water clusters.[10]In addition, proton transfer in liquid water is intimately connected to the reorganization of the hydrogenbonded network of the water solvent. Sofronov and Bakker reported that nanoconfinement leads to very strong slow-down effects on the rate of aqueous proton transfer.[11]
With the recent development of machine learning, new theoretical approaches such as neural networks have been introduced to explore the process of proton transfer. Based on the combination of the computationally efficient neural network potential with enhanced sampling techniques, Andrade et al. have constructed the free energy surface for water and proton transport at the TiO2–liquid water interface and performed MD simulations to study the dynamics of interfacial water at time scales well beyond traditional ab initio MD.[12]Their simulation results support a picture of predominantly molecular adsorption on the defect-free anatase TiO2(101) surface in contact with liquid water at ambient conditions,with a tiny fraction(∼5.6%)of water dissociation at the interface.[12]This work not only solves the longstanding problem of whether or not water would dissociate spontaneously on defect-free anatase TiO2(101), but also demonstrates the vital role of proton transfer in the adsorption form of interfacial water.
In the process of proton transport, the nuclear quantum effects (NQEs),[13–16]that is, the quantum motion of hydrogen atoms,play an important role. Accurate measurement and analysis of the nuclear quantum effects of hydrogen atoms are challenging both theoretically and experimentally. Recent progress in experimental techniques of measurements includes deep inelastic neutron scattering[17,18]and inelastic electron tunneling spectroscopy.[19]For precise theoretical research,path integral molecular dynamics(PIMD)using interaction potentials from first-principles,i.e.,ab initio PIMD,[20]is mainly employed. Due to the huge amounts of computational resources required in ab initio PIMD calculations, it is extremely difficult to apply this method to deal with the NQEs of hydrogen atoms during their transport processes.Apparently, alternative approaches are prerequisites to treat the NQEs of proton transfer.
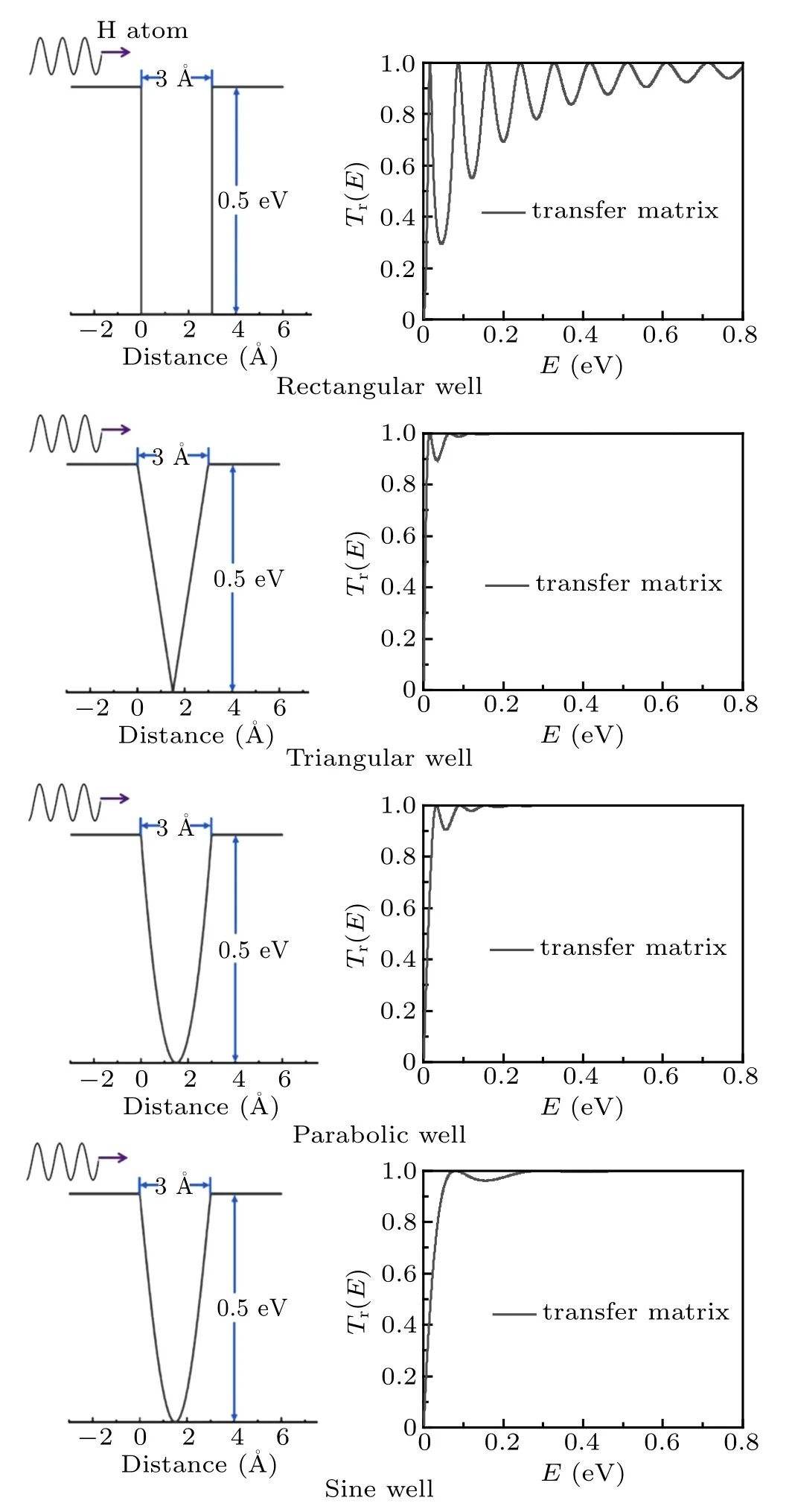
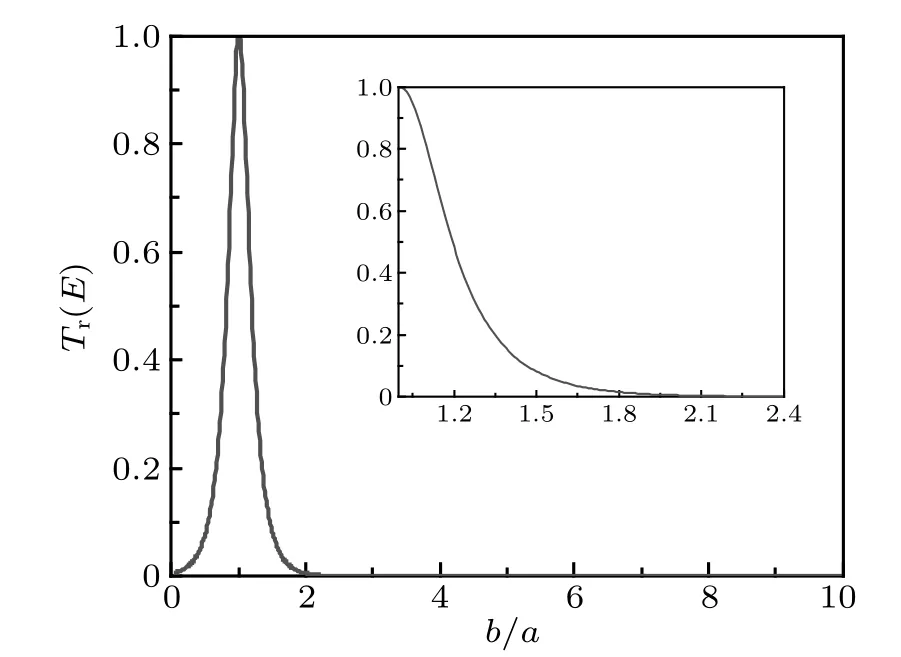
Recently, based on the method of transfer matrix (TM)in combination with first-principles calculations,[21]we have studied the NQEs of H diffusion on the Pt(111) surface, and predicted the existence of atomic-scale resonance transmission phenomenon, i.e., atomic resonant tunneling(ART).For one-dimensional rectangular double barriers, the mathematical relation between the incident energy(Ei),the barrier height(Eb),and the energy and geometric parameters describing the double barriers has been established[22]for the resonant tunneling of quantum particles,in which 100%transmission takes place when Ei We begin with investigating the transmission probability of individual H atoms passing through some model potentials of simple forms, as shown in Fig.1. Four different types of single barriers (rectangle, triangle, parabola, and sine) with a width of 3 ˚A and a height of 0.5 eV are considered and compared. The single barrier width,3 ˚A,is approximately the lattice spacing between the same type of adjoining surface sites(top-top,hcp-hcp,fcc-fcc)on Pt(111)surface.[21]As schematically shown in Fig.1, the incident H atoms are from the left side of the barriers in the form of plane waves.The right panels of Fig.1 display the transmission probabilities obtained from the TM method and the semi-classical method, the Wentzel–Kramers–Brillouin(WKB)approximation,[23]to make a comparison. For a given energy barrier V(x), the latter computes the transmission probability as follows: for V(x)>E within the interval a ≤x≤b, with m being the particle mass;and Tr(E)=1 when V(x)≤E. From Fig.1,one sees that for all types of barriers the values of Tr(E)increase sharply when the incident energy is close to the barrier height(Eb=0.5 eV).Moreover, for the energy range of E Fig.1. Schematic diagram of H atoms crossing different types of single barriers (left panels), and the comparison of transmission probability calculated by the TM and WKB method(right panels),as a function of the incident energy E. As shown in Fig.1, when the incident energy is greater than 0.5 eV, the transmission probability calculated by TM method shows significant oscillation, while WKB can only give the result of complete transmission. This is another important feature that distinguishes quantum particles from classical ones. The reason why the quantum oscillations obtained by TM method are washed out in WKB approximation lies in the fact that the role of phase factors of particle wave functions which would induce quantum interference is explicitly included in TM method[21]while is absent in WKB. In addition, it can be found that the transmission behavior of the triangular, parabolic, and sine barriers with relatively similar barrier shapes is also similar. In particular, the transmission probabilities of the parabolic and sine barriers are almost the same. Compared with the rectangular single barrier, the potential fields change much more smoothly in the triangular,parabolic, and sine barriers; and the probabilities of barriercrossing increase monotonically with the particle energy and finally approach 1. When the incident energies are higher than the barrier height,there is no quantum oscillation behavior as observed when crossing the rectangular barrier. This implies that the rate of change of the barrier in real space, dV/dx,may have nontrivial effects on the transmission behavior when passing through a given potential filed.For the situation where the potential changes drastically, such as the rectangular barrier,there will be significant quantum oscillations in the transmission probability. In the following, one can see that for single potential wells and double barriers, such a qualitative trend of variation still holds. Using the TM method,the transmission coefficient across a single rectangular barrier(barrier height:V0;barrier width: a)may be expressed as follows: It is clear that the long-range oscillations originate from the second term which oscillates as a sine function of the incident energy,to large distances well above the barrier width. Fig.2. Similar to Fig.1 but for H passing through different types of single potential wells,which are studied using the TM method only. Meanwhile, it can be seen that for the rectangular single potential well,there are significant oscillations for the incident energies well above the first energy point of resonant tunneling. For the other types of potential wells,however,after reaching the first peak of resonant tunneling,the variations of the tunneling probability are relatively flat and converge quickly to full transmission. This is similar to the situation of a single barrier,for which sharp changes present at boundaries of the potential field, and significant quantum oscillation occurs in the transmission probability;while transmission across the other three types of potentials wells shows much smaller magnitude of oscillations and converges quickly to 1. Fig.6. Similar to Fig.3 but for protons across hetero-structured double barriers which consist of single barriers of different widths but the same type. In this section, we perform theoretical analysis on the general transmission properties of quantum particles across hetero-structured double barriers, based on the analytic calculations using the TM method. We firstly consider rectangular barriers. As illustrated in Fig.7(a), for a single rectangular barrier, the wave functions on the left and right sides upon transmission across the barrier may be expressed in the following form: For double barriers which consist of single rectangular barriers with the same height (V0) but different widths (a and b,respectively),and with a barrier-barrier spacing of w,the total transfer matrix is given by Fig.7. (a)Schematics of scattering and transmission of a quantum particle by a potential barrier V(x). (b)Translation of V(x)by a distance. The total transmission coefficient is given by Based on the results for single rectangular barriers,[21]each component of the matrix element M11may be explicitly written as below: After substitution with the expressions presented in Eqs.(10a)–(10b),straightforward calculations give Consequently,the total transmission coefficient of a quantum particle passing across the hetero-structured rectangular double barriers is readily obtained using Eq.(9). To further demonstrate the key difference that distinguishes hetero-structured double barriers from homostructured double barriers,i.e.,the existence or absence of resonant transmission,we have calculated the transmission coefficient of proton as a function of the ratio of the barrier width,b/a, for a given incident energy E =0.184 eV, which gives ART for homo-structured rectangular double barriers shown in Fig.3. During the calculations, the barrier height is kept at 0.2 eV with a barrier–barrier spacing of w=1.4 ˚A,and the width of the first barrier is kept at a=1 ˚A while the width of the second barrier varies from b=0.05 ˚A to 10 ˚A.The results are shown in Fig.8. Within the range of variation under consideration (0.05 ≤b/a ≤10), it can be seen that if and only if b/a=1,i.e.,when the double barriers are homo-structured,the phenomenon of ART can happen. Fig.8. Calculated transmission coefficients of protons transferring across hetero-structured rectangular double barriers, as a function of barrier width ratio. We have studied the nuclear quantum effects(NQEs)on the processes of protons transferring across one-dimensional potentials fields(potential barriers and potential wells)by using the method of transfer matrix(TM),which is numerically accurate for the description of quantum particles transport in one-dimensional(1D)or quasi-1D systems.For the transfer of protons across single barriers,the transmission coefficients depend critically on the geometries of the barriers,where strong quantum oscillations are found in the case of rectangular barriers. The phenomenon of resonant transmission, i.e., atomic resonant tunneling (ART) of protons is demonstrated in various types of model potentials (single potential wells, homostructured double barriers).By contrast,our calculations show that,ART is absent in hetero-structured double barriers which consist of single barriers of the same height but of different geometries. As an example of typical model potentials, rectangular hetero-structured double barriers are studied analytically and the mathematical expressions have been derived for the transmission coefficients of quantum particles in general.The absence of ART is again demonstrated by numerical calculations for rectangular hetero-structured double barriers.2. Results&discussion
2.1. Numerical calculations based on the TM method


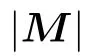









2.2. Theoretical analysis on hetero-structured rectangular double barriers
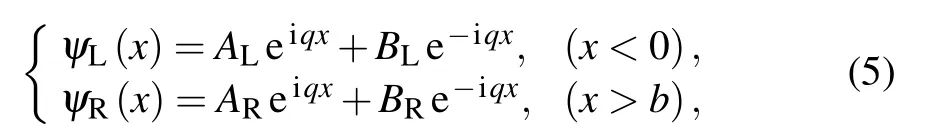
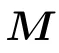
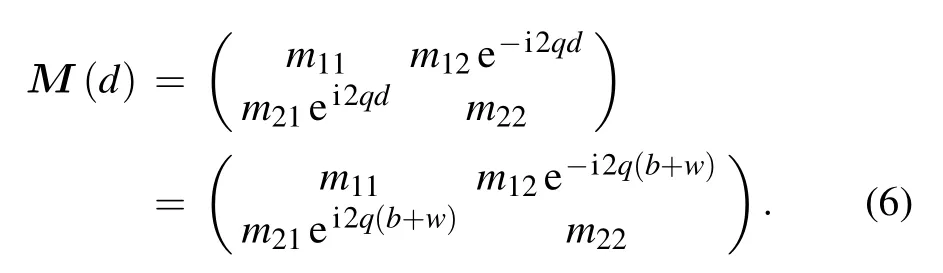
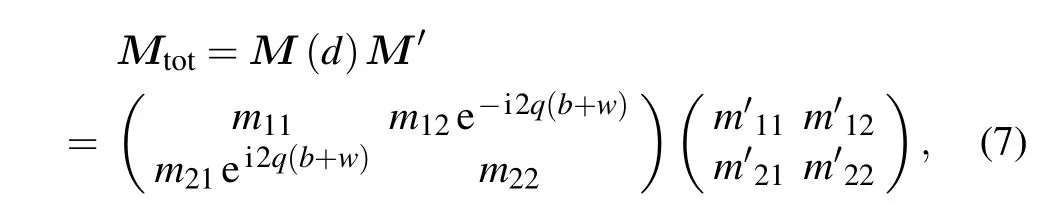
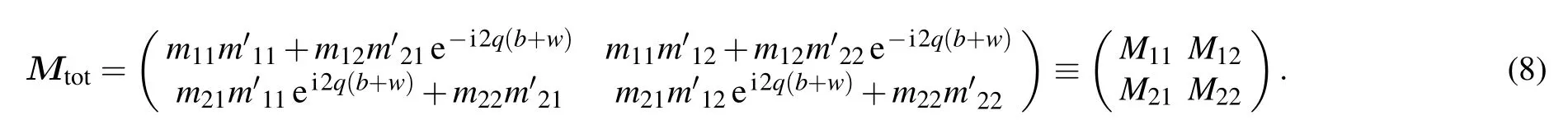





3. Conclusions

