低渗透介质中轻非水相流体迁移转化规律

阮冬梅,卞建民*,王 倩,吴娟娟,王 宇,孙晓庆

低渗透介质中轻非水相流体迁移转化规律

阮冬梅1,2,卞建民1,2*,王 倩1,2,吴娟娟1,2,王 宇1,2,孙晓庆1,2

(1.吉林大学地下水资源与环境教育部重点实验室,吉林 长春 130021；2.吉林大学新能源与环境学院,吉林 长春 130021)

本文利用COMSOL软件建立轻非水相流体(LNAPL)纵向迁移转化模型,采用有限单元法进行求解,预测污染物分布规律,并利用局部分析法进行参数敏感性分析.结果表明,大部分LNAPL会在水面以上聚集形成高的质量分布峰值区域,少部分克服毛细压力向下迁移,在自由相迁移范围内,其溶解相浓度达到或接近饱和溶解度;当顶部污染源消失后,降水会使最大饱和度和浓度出现的深度逐渐下移;多孔介质中的低渗透镜体会使污染物垂向入渗受阻,在其表面聚积形成污染池;渗透系数是控制LNAPL纵向迁移速度及饱和度分布的关键参数.

多孔介质；轻非水相流体；多相流；数值模拟；参数敏感性分析

水资源已成为制约我国经济社会发展的重要因素[1-4],而石油作为工业发展的必备能源,其大量使用造成的地下水污染问题尤为突出[4-6].大部分的石油污染物为不溶于水的非水相流体(NAPLs),NAPLs根据其密度分为两种类型[7],密度小于水的非水相液体(LNAPL)和密度大于水的非水相液体(DNAPL).泄露在地表的NAPLs类污染物在降雨、重力和毛细力等作用下通过包气带进入含水层[7-8],在这个过程中,自由相的NAPLs将受到土壤介质中的有机和无机胶体的吸附作用,同时不断地发生溶解和挥发作用,其迁移转化是一个非常复杂的过程,在地下环境中呈现自由态、溶解态、固态和气态等多相共存的特征[9-14].近几十年以来,关于NAPLs在多孔介质中的多相分布、迁移规律等方面的内容,国内外学者进行了大量的室内实验,分析其在地下水环境中的行为[15-18],并建立相关数学模型模拟其迁移转化规律[19-22].截至目前,研究内容主要集中于NAPLs在渗透性较好的均质多孔介质含水层中的纵向迁移、横向迁移以及非均质介质中污染池的形成等方面,而关于NAPLs在低渗透介质含水层中纵向迁移转化机理的研究内容则较少.粉质黏土属于黏性土,粒径小,透水性极差,是一种典型的低渗透介质,普遍被认为具有较好的隔污性能,除此之外,相比于粗砂等渗透性较好的介质,粉质黏土中黏粒含量高、介质吸附性能较好,对有机污染物的迁移过程影响显著.因此,研究者大多认为NAPLs在其中的迁移方式与在砂土中有所不同,由于地下水流速缓慢,对流作用不再是污染物的主要迁移方式[22-24],有学者通过数值模拟手段研究粉质黏土中DNAPL的迁移规律,结果显示DNAPL迁移速度十分缓慢,在几十年内无法造成土体深部污染,对流弥散作用弱,污染物的纵向迁移主要受渗透系数以及饱和度—毛细压力(S-P)关系的影响[25]综上所述,粉质黏土渗透性弱,地下水流速缓慢,吸附能力强,NAPLs在其中的迁移转化特征与透水性好的介质有所不同.因此,正确认识粉质黏土中LNAPL在饱和多孔介质中的运移机制和污染特征对东北地区广泛分布的低渗透介质粉质黏土中地下水污染防治与修复有着重要意义.本文重点研究了污染物持续注入条件下LNAPLs在饱和粉质黏土中的迁移转化规律和不同泄漏条件下污染物的污染特征.分析了各个模型参数对输出值饱和度的影响,为了结果的直观性,采用局部分析法,分别设置了6个变幅对比分析参数对饱和度的影响程度.

1 LNAPL在饱和多孔介质中迁移转化模型的建立

LNAPL在饱和多孔介质中迁移转化的概念模型主要涉及介质的性质、流体的性质、各相间的相互转化以及多相流运移机制.

1.1 LNAPL的存在状态及相互转化过程的控制方程

LNAPL在饱和多孔介质中的存在状态有3种,即自由相LNAPL、溶解相LNAPL以及吸附于多孔介质颗粒上的固相LNAPL.同时,这3种相态之间存在相互转化,自由相LNAPL吸附于颗粒及其逆过程、自由相LNAPL溶解于水中、溶解相LNAPL吸附于颗粒及其逆过程,具体转化关系如图1所示.

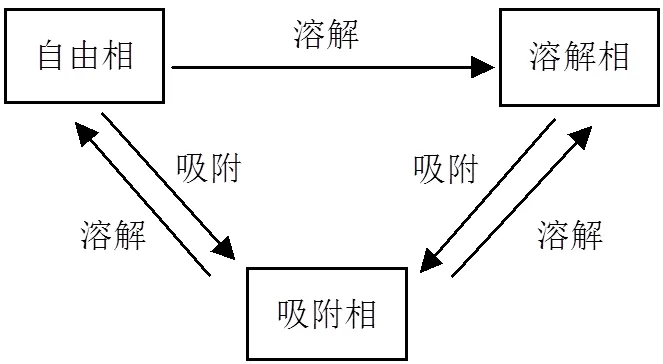
图1 非水相流体三相转化过程

多孔介质中LNAPL溶解进入水相的过程表达式如下:

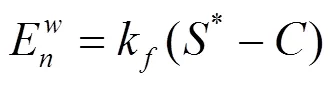
多孔介质中LNAPL吸附于介质的过程可用线性平衡吸附模型表示,公式如下:

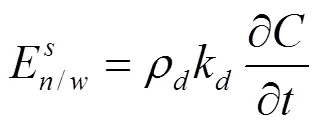
1.2 LNAPL迁移的控制方程

1.2.1 流速方程 在多孔介质中,多相流的运动速度缓慢,各相的流速符合达西定律,公式如下:

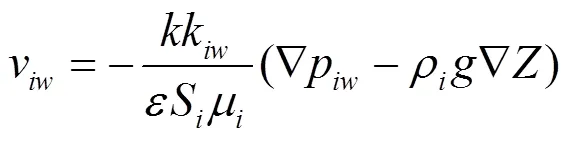
式中:为介质固有渗透率,m2;k为各流体的相对渗透率,m2;为介质的孔隙度;S为各流体的饱和度;μ为各流体的粘滞系数,mPa/s;ρ为各流体的密度, kg/m3;p为各流体的压力,Pa.

1.2.2 水相和自由相LNAPL的流动方程 水相和自由相LNAPL的流动过程符合达西定律,基于质量守恒定律构建其流动方程,公式如下[19]:

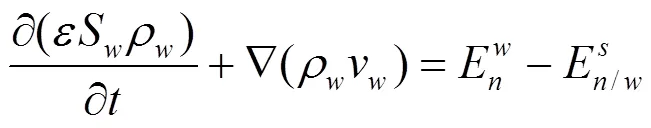
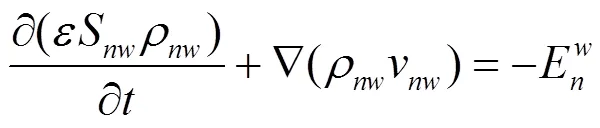
式中:为介质的孔隙度;S为各流体的饱和度;v为各流体的达西流速,m/s;ρ为各流体的密度,g/cm;E和E分别为溶解速率和吸附速率,kg/(m3×s).

1.2.3 对流—弥散方程 溶解相LNAPL 在多孔介质中的迁移受对流、弥散作用的控制,基于质量守恒定律,构建对流—弥散方程,公式如下[19]:

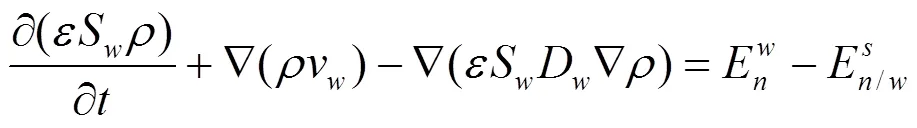
式中:D为水动力弥散系数,m2/s.

1.2.4 毛细压力、相对渗透率、饱和度关系 对于S-P关系,本文采用学者van Genuchten[27]提出的模型,其表达式如下:

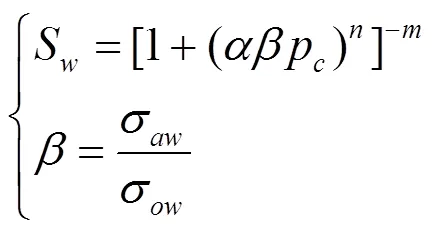
式中:为水—气表面张力与LNAPL—水的表面张力的比值;和为土水特征曲线的参数,且1-1/.

对于kr-S关系,本文采用学者Mualem[28]提出的模型,其表达式如下:

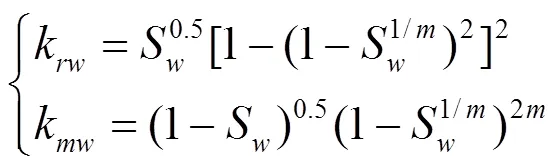
1.2.5 模型的定解条件 初始条件通常指的是＝0时刻的饱和度、组成成分等条件,通常有下面一些变量需要指定初始条件.

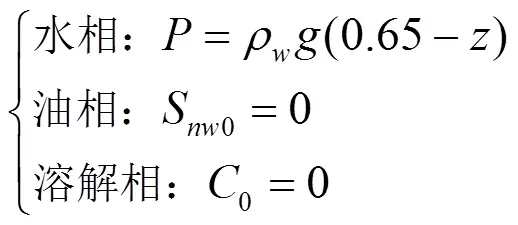
模型的边界条件如下所示:

(1)右边界

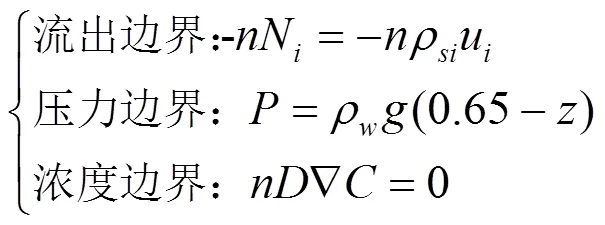
(2)左边界:轴对称边界

(3)下边界

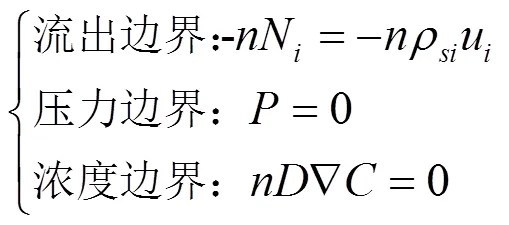
(4)上边界

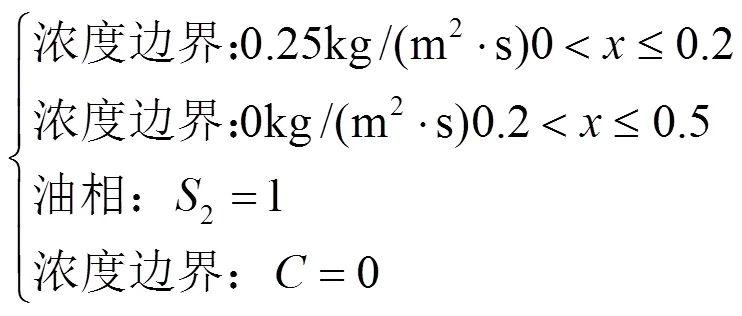
1.3 数值模拟方法与求解

模拟采用的软件COMSOL是一款大型的高级数值仿真软件,最大的优势是具有杰出的多场直接耦合分析能力,可以选择软件自有的模块实现多物理场耦合求解.

根据场地条件,设计模拟对象LNAPL在50cm´65cm的二维砂箱中发生泄漏,介质为粉质黏土,假定模型初始呈饱和状态,污染物以0.25kg/(m2s)的速度持续注入.模型所需参数设定具体如表1所示[28-30].介质的固体骨架发生形变较小,可忽略.在LNAPL的迁移过程中,介质的干密度、孔隙度以及固有渗透率不随时间发生改变;流体的密度、动力粘滞系数、表面张力等性质则主要受温度和压力的控制,在流体迁移过程中,假设温度和压力不发生变化.根据以上内容假定本次模拟的各个参数不发生变化.

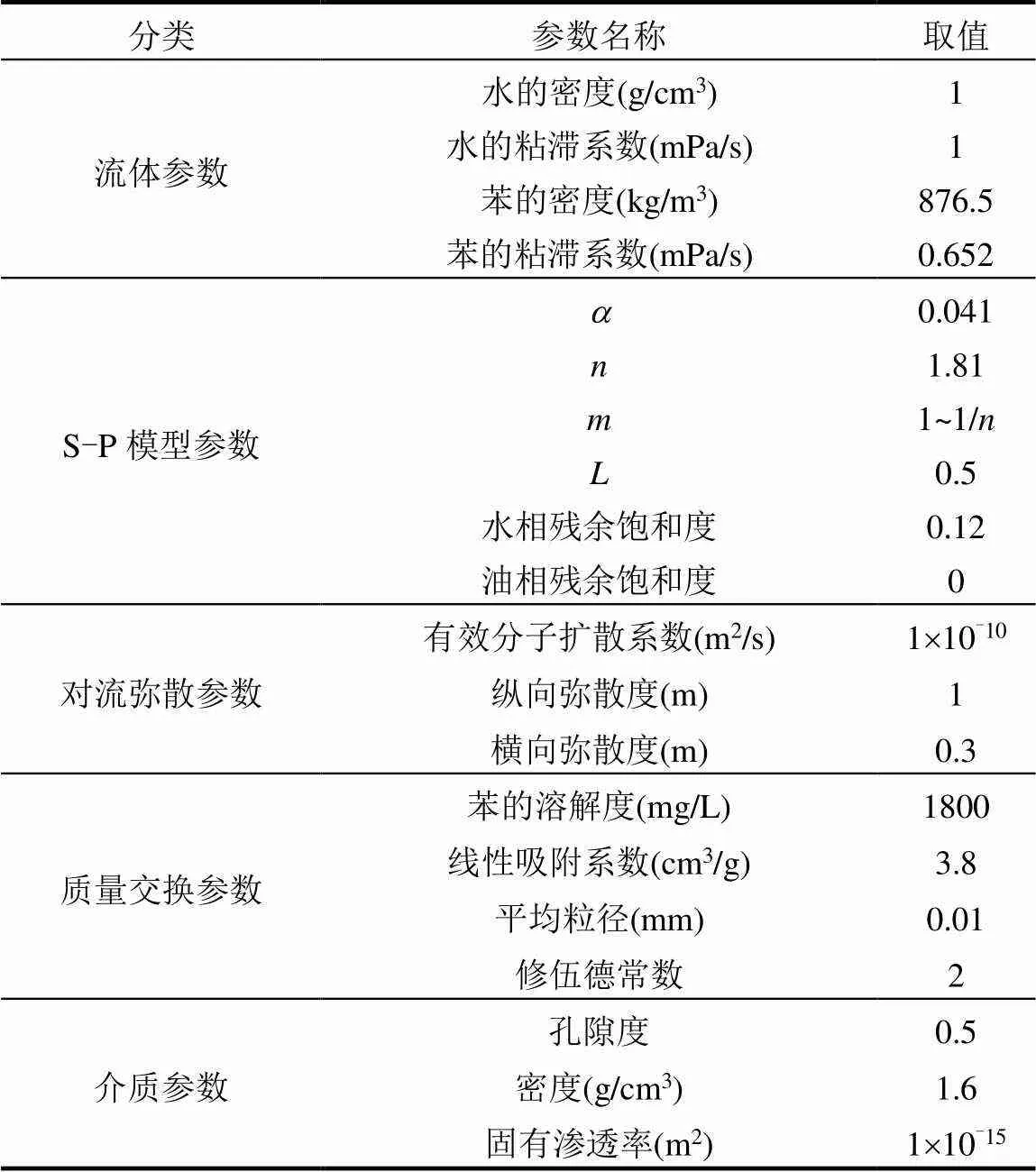
表1 模型参数确定值

2 结果与讨论

2.1 饱和粉质黏土中LNAPL的迁移转化规律

结合上述数学模型和给定的参数值,运行COMSOL软件进行模拟,模拟总时长为600s,分别获得LNAPL自由相的饱和度和压力分布、溶解相的浓度分布以及非水相的相对渗透率分布情况.

2.1.1 自由相饱和度和溶解相浓度的分布规律 由图2(a)可知,LNAPL的密度比水小且溶解度较低,大部分在水面以上聚集并侧向运移,形成了高的质量分布峰值区域,孔隙中的水被LNAPL驱替饱和度在水面处最大.因此,如图2(c)在水面附近溶于水相的LNAPL的浓度很低.同时,LNAPL在重力的作用下克服毛细压力,驱替孔隙中的水继续向下迁移,其迁移速率小于侧向迁移.在这个过程中,自由相LNAPL与水相充分接触,溶解进入水相,因此在属于自由相的分布区域内,溶解相的浓度均很高,达到或者接近其在环境中的饱和溶解度.而根据图2(b)、2(d)分析可知,随着模拟时间的延长,污染物入渗锋面出现的深度也逐渐下移,饱和度随着深度的增加逐渐减小,溶解相锋面出现的深度也逐渐下移,并且由于机械弥散作用,溶解相的最大迁移深度大于自由相.

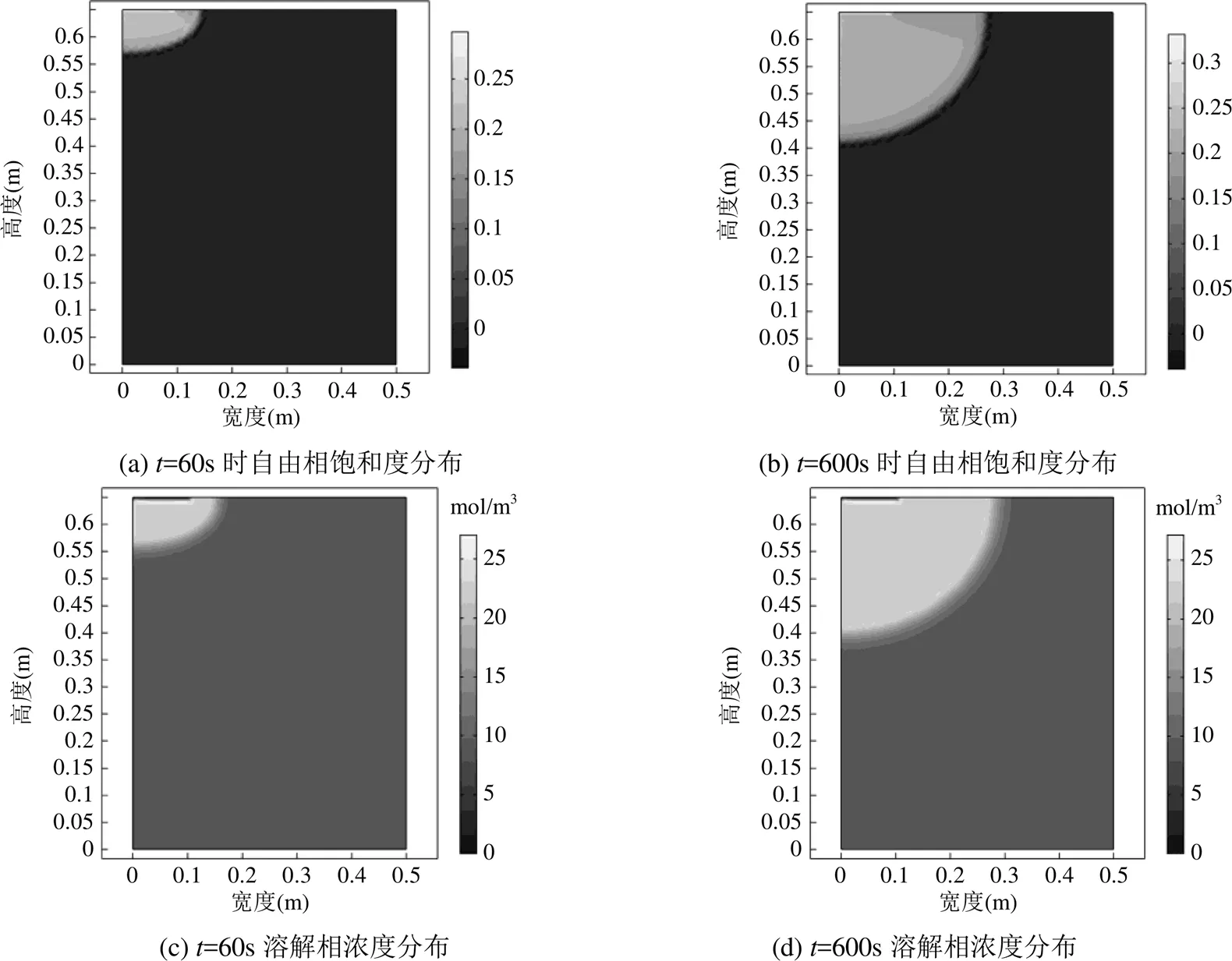
图2 自由相饱和度和溶解相浓度分布

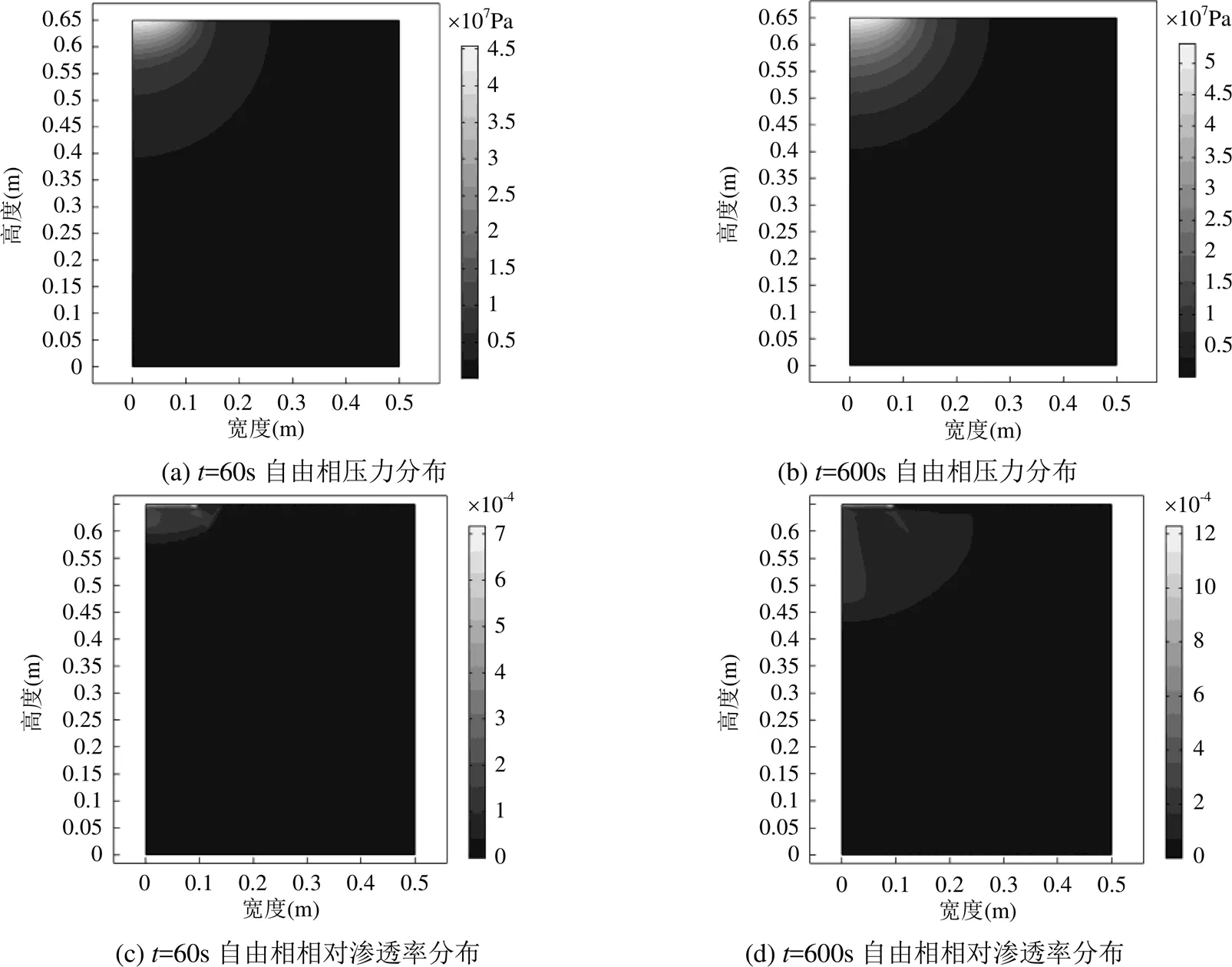
图3 自由相压力和相对渗透率的分布

2.1.2 LNAPL压力和相对渗透率的分布规律 LNAPL的压力大小和相对渗透率与饱和度大小有关,饱和度的减小会使得两者的值减小.因此,压力和相对渗透率的变化规律与饱和度的变化规律呈现一致性.由图3(a)、3(c)分析可知,由于LNAPL在水面上形成了高的质量分布峰值区域,因此,在水面附近LNAPL的压力和相对渗透率值最大.同时,LNAPL会在重力的作用下克服毛细压力向下迁移,越靠近水面,孔隙中污染物占据的体积越多,压力和相对渗透率值越大.而根据图3(b)、3(d)分析可知,随着模拟时间的延长,污染物入渗锋面出现的深度也逐渐下移,饱和度随着深度的增加逐渐减小,压力和相对渗透率的值也逐渐减小.

2.1.3 模型验证 为了确保数值模型的适用性,将模拟结果与实测数据进行对比验证,而毛细压力—饱和度关系是描述水—油两相流迁移的重要模型.因此,本文将土壤水分特征曲线的模拟结果与实测数据进行拟合,结果如图4所示.从图中可以看出二者的拟合关系较好,验证了模拟结果的可靠性.

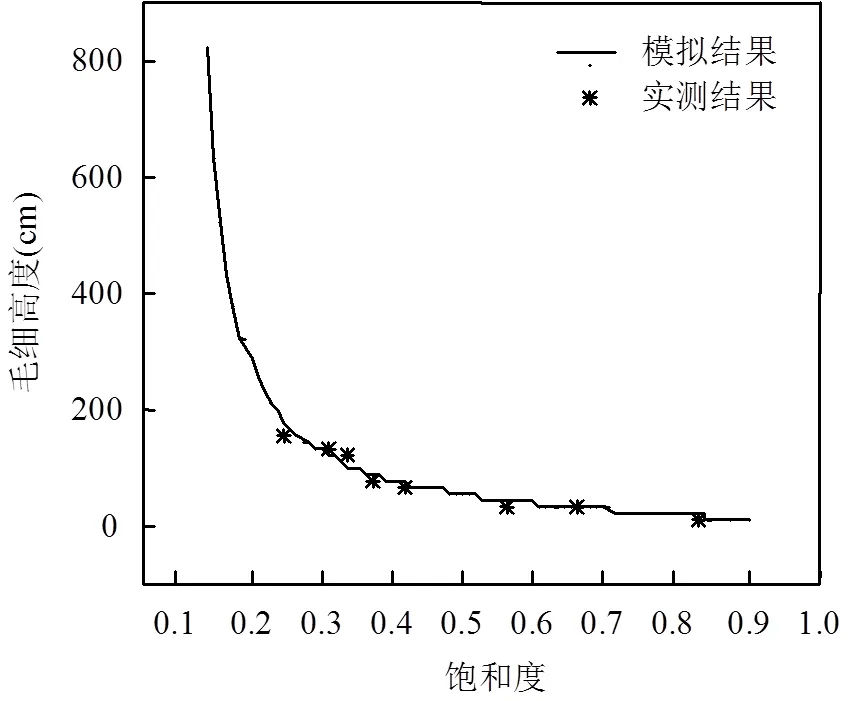
图4 土壤水分特征曲线模拟结果与实测数据拟合

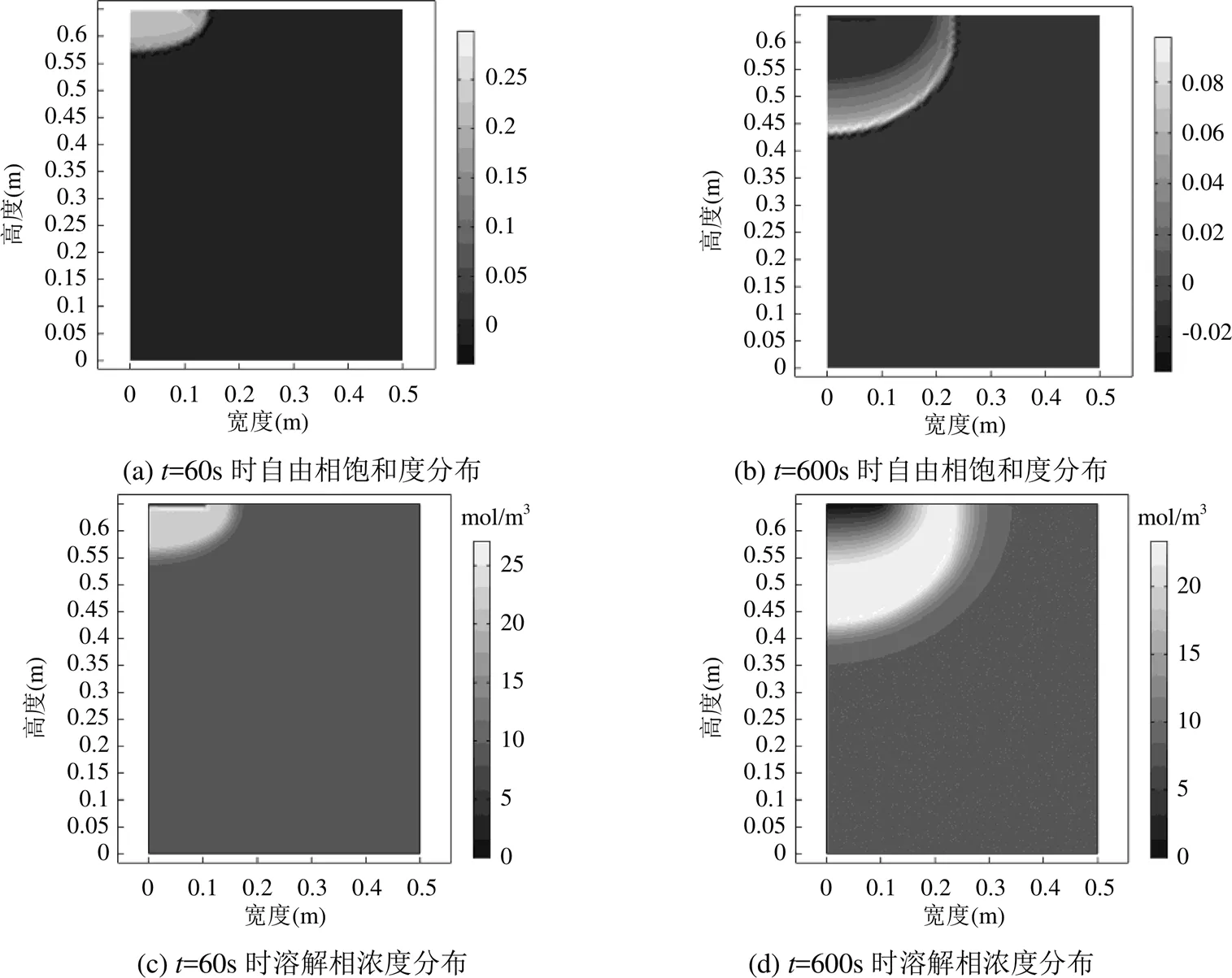
图5 短时间泄漏条件下自由相饱和度和溶解相浓度分布

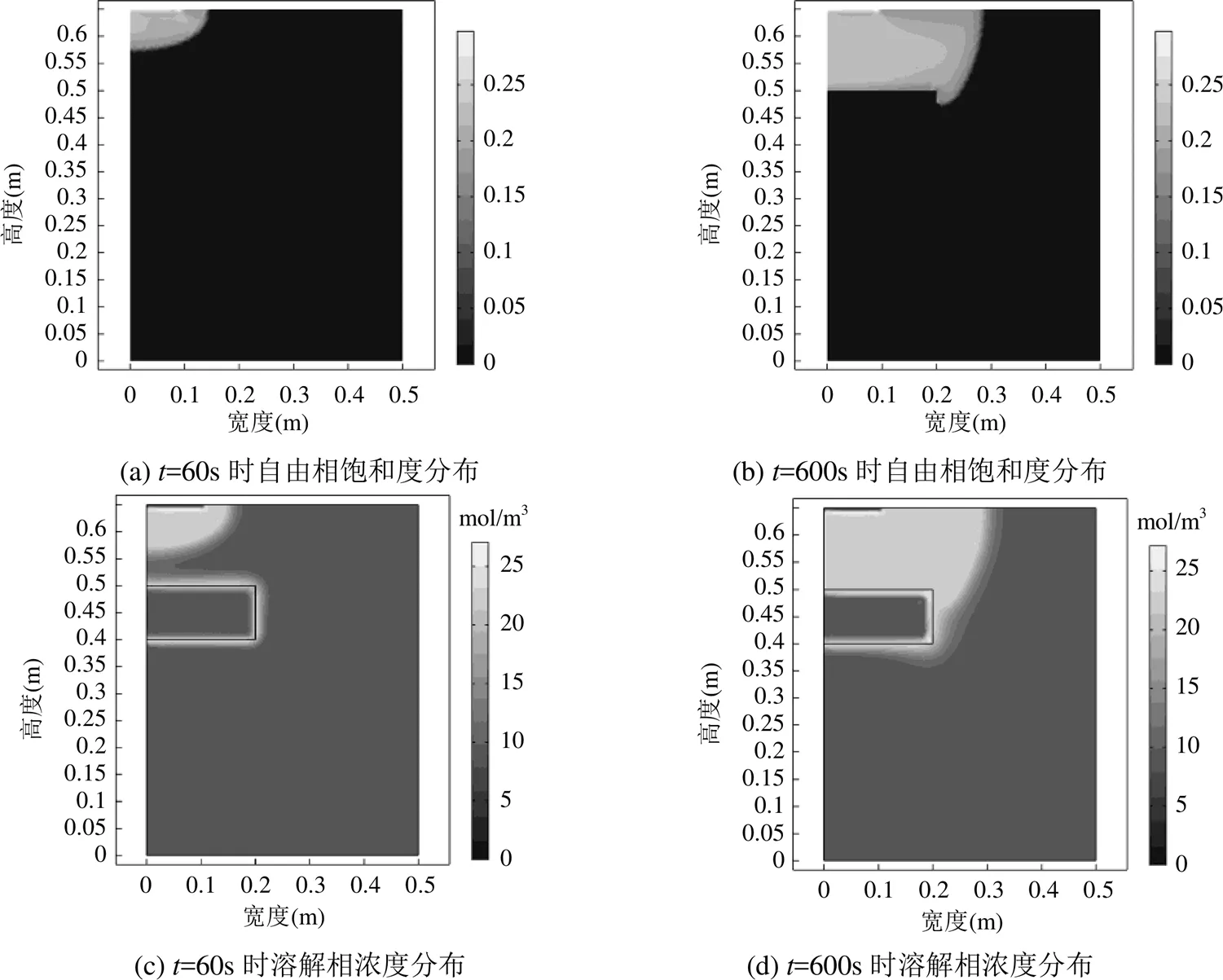
图6 存在低渗透镜体时自由相饱和度和溶解相浓度的分布

2.2 污染物迁移情景预测

由于储存不当导致LNAPL泄漏到地下环境时,会有不同的泄漏方式和场地介质条件.通过模拟研究短时间泄漏条件下以及土体中存在低渗透夹层时LNAPL的迁移特征.

2.2.1 短时间泄漏情景预测 模拟的过程如下:模型初始呈饱和状态,污染物持续注入100s之后水相以相同的速度入渗,模拟时长为600s.不同时刻模拟结果如图7所示.

由图5(a)、5(c)可知,污染物持续注入的时间内,其迁移转化规律和前文描述一致.而根据图5(b)、5(d)分析可知,在顶部污染源消失后,LNAPL在重力作用和水压下继续向下迁移,最大饱和度和浓度出现的深度也逐渐下移.在这个过程中由于质量守恒定律,输入到地下环境中的污染物总量保持不变,随着迁移深度的增加,最大饱和度逐渐减小,污染范围也逐渐增大.

2.2.2 低渗透镜体情景预测 假设研究介质(介质相关参数如表1所示)中存在低渗透镜体,透镜体具体参数如表2所示.

表2 低渗透镜体构建条件

由图6(a)、6(c)可知,在污染物锋面未抵达低渗透镜体时,其迁移转化规律如前文所示.根据图6(b)、6(d)分析可知,当LNAPL入渗锋面达到介质中低渗透镜体时,由于透镜体内的介质孔隙较小,毛细压力大,而此时透镜体上聚集的自由相LNAPL较少,其重力不足以克服毛细压力.因此自由相LNAPL停止垂向入渗,在透镜体上方聚集,饱和度不断增大,压力也逐渐增大,引起侧向水平运动,在这一过程中,溶解相的垂向运移也受阻,透镜体内浓度很低.而当污染羽绕过透镜体边缘时,重力大于毛细压力,自由相和溶解相将继续向下迁移.

2.3 参数敏感性分析

参数的不确定性会使得模拟结果产生误差,目前分析参数敏感性的方法主要有两种,分别是局部敏感性分析方法和全局性敏感性分析方法.前者具有操作简便、快捷高效的优点.因此,本文采用局部敏感性分析的方法来分析S-P 模型参数,LNAPL 的密度、动力粘滞系数、溶解度以及介质的线性吸附分配系数等参数对污染物运移规律的影响,以初始值为基础,参数变幅设置为±30%进行对比分析,具体参数设置值见表3,计算得到LNAPL 在多孔介质中运移600s后的质量分布情况.

为了探究不同参数对输出值的敏感程度,通过以下公式计算敏感指数,绝对值越大,说明该参数敏感性越高.

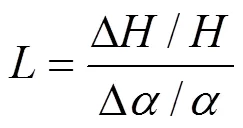
式中:为敏感性指数(无量纲); Δ/为输出值的变化率,将输出值定为饱和度;Δ/为参数的变化率.

2.3.1 S-P模型参数 S-P模型参数是两相流迁移最基本也是最重要的参数,本文通过调整缩放系数来探究其对非水相流体迁移的影响.计算结果如图7(a)所示,不同参数条件下,各曲线基本完全重合,表明参数对饱和度的纵向分布影响不明显,只是略微增大了污染物的迁移深度.而参数是S-P曲线的缩放系数,相同饱和度下,越大毛细压力越小,而毛细压力是两相流迁移的重要驱动力之一,因此迁移深度会有所增大,符合一般规律.

表3 参数设置值

2.3.2 LNAPL的物理性质 为了探究污染物自身性质对迁移规律的影响,设置不同变幅的污染物密度和溶解度参数值进行对比分析,计算结果如图7(b)、7(c)所示.的增大使得污染物的上部质量分布有所增大.密度主要是通过影响非水相流体的另一个驱动力—重力来影响其迁移特征,LNAPL在重力的驱动下向下迁移,密度越小,重力越小,其迁移速度越慢,上部质量分布越多;模型呈饱和状态,为LNAPL的溶解提供了很好的环境条件,因此溶解度()的大小会对其质量分布产生一定影响.结果显示溶解度越大,溶解于水相的LNAPL越多,孔隙中自由相LNAPL的质量分布减小.

2.3.3 质量交换参数 LNAPL的粘滞系数()主要是通过影响渗透系数而间接影响污染物迁移速度,不同粘滞系数值计算得到的LNAPL质量分布情况如图7(d)所示.对比分析可知,LNAPL粘滞系数减小,渗透系数随之增大,迁移深度和迁移速度也明显增大,上部的质量分布减小;吸附分配系数d的大小,代表了土壤有机质含量的多少,而有机质含量越高,介质吸附有机污染物的能力越强,对污染物运移的阻碍作用越强.计算结果如图7(e)所示,对比分析可知,分配系数增大会使得迁移深度和迁移速度略微降低,下部质量分布减小.

2.3.4 不同参数的敏感性响应 不同参数设置条件下,以污染物迁移距离为输出值,导出结果如图7(f)所示,由图可知参数与迁移距离呈正相关关系;参数、d与迁移距离呈负相关关系.其中,参数对输出结果的影响最为显著,间接说明渗透系数是影响污染物迁移的关键因素.但是敏感指数的绝对值均较小,说明污染物迁移距离受参数影响产生的变化较小.

3 结论

3.1 在饱和低渗透介质粉质黏土中,LNAPL大部分漂浮在水面形成高的质量分布峰值区域,同时由于地下水流速缓慢,自由相LNAPL主要在重力和毛细压力的作用下纵向迁移,在该范围内,溶解相达到或接近饱和溶解度,并且溶解相迁移深度大于自由相.

3.2 当顶部污染源消失后,降水会使得非水相流体最大饱和度和浓度出现的深度逐渐下移; 多孔介质中的低渗透镜体会使LNAPL垂向运移受阻,在其表面聚积并开始侧向运移,直到污染羽前缘绕过透镜体边缘时,LNAPL重力克服毛细压力向下运动.

3.3 模型参数对于非水相流体的迁移特征都存在一定的影响,参数敏感性分析结果显示粘滞系数是控制LNAPL纵向迁移速度及饱和度分布的关键参数,也间接表面了渗透系数对于低渗透介质中非水相流体迁移的重要性.

[1] 王 涵,卢文喜,李久辉,等.地下水DNAPLs污染多相流的随机模拟及其不确定性分析 [J]. 中国环境科学, 2018,38(7):2572-2579. Wang Han, Lu Wen-xi, Li Jiu-hui, et al. Stochastic simulation and uncertainty analysis of multi-phase flow of groundwater polluted by DNAPLs [J]. China Environmental Science, 2018,38(7):2572-2579.

[2] 朱振慧,高宗军,张晓海,等.轻质非水相流体(柴油)在多孔介质中的垂向运移 [J]. 环境工程学报, 2015,(4):1842-1848. Zhu Zhen-hui, Gao Zong-jun, Zhang Xiao-hai, et al. Vertical migration of LNAPLs (diesel) in porous medium [J]. Chinese Journal of Environmental Engineering, 2015,(4):1842-1848.

[3] 莫龙庭.DNAPL污染源识别和多相流及生物堵塞模拟研究[D]. 南京:南京大学, 2016. MO Long-ting. Source search algorithm application and modeling of DNAPL transportation and remidiation [D]. NanJing: NanJing University, 2016.

[4] 杨明星,杨悦锁,杜新强,等.石油污染地下水有机污染组分特征及其环境指示效应 [J]. 中国环境科学, 2013,33(6):1025-1032. YANG Ming-xing, YANG Yue-suo, DU Xin-qiang, et al. Organic fractious and their environmental implications of petroleum contaminated groundwater [J]. China Environmental Science, 2013, 33(6):1025-1032.

[5] 王金成,井明博,张绍鹏,等.不同生物质炭对陇东黄土高原石油污染土壤的修复作用 [J]. 中国环境科学, 2020,40(6):2565-2576. WANG Jin-cheng, JING Ming-bo, ZHANG Shao-peng, et al. Remediation effects of the different biochars on crude-oil contaminated soil in eastern Gansu Province of the Loess Plateau [J].China Environmental Science, 2020,40(6):2565-2576.

[6] 任 慧.高浓度石油污染土壤异位—原位联合生物修复技术研究[D]. 济南:山东师范大学, 2015. REN Hui. Research of ectopic joint in-situ bioremediation technology for high concentrations of petroleum contaminated soil [D]. Jinan: Shandong Normal University, 2015.

[7] Alazaiza M Y D, Ngien S K, Bob M M, et al. Non-aqueous phase liquids distribution in three-fluid phase systems in double-porosity soil media: Experimental investigation using image analysis [J]. Groundwater for Sustainable Development, 2018,7:133-142.

[8] 杨明星.石油有机污染组分在水位波动带中的分异演化机理研究[D]. 长春:吉林大学, 2014. YANG Ming-xin. Fate and Transport of Petroleum organic Compounds in Water Table Fluctuation Zone [D]. Changchun: Jilin University, 2014.

[9] 高燕维,郑 菲,施小清,等.基于透射光法探讨水流流速对DNAPL运移分布的影响[J]. 环境科学, 2015,36(7):2532-2539. GAO Yan-wei, ZHENG Fei, SHI Xiao-qing, et al. Laboratory Investigation of DNAPL Migration Behavior and Distribution at Varying Flow Velocities Based on Light Transmission Method [J].Environmental Science, 2015,36(7):2532-2539.

[10] 胡黎明,邢巍巍,吴照群.多孔介质中非水相流体运移的数值模拟[J]. 岩土力学, 2007,28(5):951-955. HU Nin-ming, XIN Wei-wei, WU Zhao-qun. Numerical simulation of non-aqueous phase liquids migration in porous media [J]. Rock and Soil Mechanics, 2015,36(7):2532-2539.

[11] 赵 雷.饱和多孔介质内多组分非水相有机物溶解传递机制研究[D]. 天津:天津大学, 2015. ZHAO Lei. Dissolution and transfer mechanism of multi-components non-aqueous phase organic liquids in saturated porous media [J]. Tianjin: Tianjin University, 2015.

[12] Bear J. Dynamics of Fluids in Porous Media [J]. Journal of Fluid Mechanics, 1973,61(1):206-208.

[13] Ngien S K, Ken T L. Numerical model for NAPL migration in double-porosity subsurface systems [J]. Proceedings of the 36thiahr world congress, 2015:5770-5774.

[14] Ruffino B, Zanetti M. Adsorption study of several hydrophobic organic contaminants on an aquifer material [J]. American Journal of Environmental Sciences, 2009,5(4):507-515.

[15] Cary J W, Simmons C S, McBride J F. Predicting oil infiltration and redistribution in unsaturated soils [J]. Soil Science Society of America, 1989,53(2):335-342.

[16] Eckberg D K, Sunada D K. Nonsteady three-phase immscible fluid distribution in porous media [J]. Water Resource Research, 1984, 20(12):1891-1891.

[17] Pantazidou M, N Sitar. Emplacement of nonaqueous liquids in the vadose zone [J]. Water Resource Research, 1993,29(3):705-722.

[18] Schroth Martin H, Istok Jonathan D, Selker John S. Three-phase immscible fluid movement in the viciniy of tex-tural interfaces [J]. Journal of Contaminant Hydrology, 1998,32:1-23.

[19] 高彦斌,张松波,李 涛,等.饱和黏性土中重质非水相有机污染物纵向迁移数值模拟[J]. 同济大学学报, 2020,48(1):24-32. GAO Yanbin, ZHANG Songbo, LI Tao, et al. Numerical analysis of vertical migration of dense nonaqueous-phase liquids in saturated clay [J]. Journal of Tongji University(Natural Science), 2020,48(1):24-32.

[20] Leverett M C. Capillary behaviour of porous soilds [J]. Trans AmInst Min Met Eng, 1941,142:152-169.

[21] 武晓峰,唐 杰,藤间幸久.多孔介质两相流的统一毛细压力饱和度关系曲线[J]. 灌溉排水, 2000,19(2):15-18. WU Xiao-feng, TANG Jie, TENG Jian-xin-jiu.Unified capillary pressure saturation relationship in porous media two phase flow [J]. Irrigation and Drainage, 2000,19(2):15-18.

[22] Geller J T, Hunt J R. Mass transfer from nonaqueous phase organic liquids in water-saturated porous media [J]. Water Resources Research, 1993,29:883-845.

[23] Essaid Hedeff I, Bekins Barbara A, Cozzarelli Isabelle M. Organic contaminant transport and fate in the subsurface: evolution of knowledge and understanding [J]. Water Resources Research, 2015,51 (7):4861-4902.

[24] Parker Beth L, Cherry John A, Chapman Steven W. Field study of TCE diffusion profiles below DNAPL to assess aquitard integrity [J]. Journal of Contaminant Hydrology, 2004,74(1/4):197-230.

[25] 余 梅.氯苯类化合物在低渗透粘性土介质中的迁移规律研究[D]. 北京:中国地质大学, 2016. YU Mei. A Dissertation Submitted to China University of Geosciences For the Doctor Degree of Philosophy [D]. Beijing: China University of Geosciences, 2016.

[26] Liao B, Aral M M. Semi-analytical solution of two-dimensional sharp interface LNAPL transport models [J]. Journal of Contaminant Hydrology, 2000,44:203-211.

[27] Van Genuchten. Closed-form equation for predicting the hydraulic conductivity of unsaturated soils [J]. Soil Science Society of America Journal, 1980,44(5):892-898.

[28] Mualem Y. A new model for predicting the hydraulic conductivity of unsaturated porous media [J]. Water Resource Research, 1976,12: 513-522.

[29] 吴照群.非水相流体在土体中运移的数值模拟[D]. 北京:清华大学, 2008. WU Zhao-qun. Numerical Modeling of NAPLs Transport in Soils [D]. Beijing: Tsinghua University, 2008.

[30] 李 晔,鹿 琪,刘 财.LNAPL迁移的数值模拟和土壤介电性质的变化分析[J]. 地球物理学进展, 2014,29(2):936-943. LI Ye, LU Qi, LIU Cai. Numerical simulation of LNAPLs migration and analysis on variation of soil dielectric properties [J]. Progress in Geophysics, 2014,29(2):936-943.

The migration and transformation of light non-aqueous fluid in silty clay.

RUAN Dong-mei1,2, BIAN Jian-min1,2*, WANG Qian1,2, WU Juan-juan1,2, WANG Yu1,2, SUN Xiao-qin1,2

(1.Key Laboratory of Groundwater Resources and Environment Ministry of Education, Jilin University, Changchun 130021, China；2. College of New Energy and Environment institute, Jilin University, Changchun 130021, China)., 2021,41(4)：1815~1823

The LNAPL longitudinal migration transformation model was established by COMSOL software, and was solved with the finite element method. It was applied to predict the distribution of pollutants, meanwhile parameter sensitivity was performed with local analysis method. The research results showed that most of the LNAPL aggregated above the water surface and formed a high mass distribution peak area, and a small part overcame the capillary pressure and migrated downward. In the free phase migration range, the dissolved phase concentration reached or approached the saturated solubility. When the top pollution source disappeared, the precipitation gradually lowered the maximum saturation and the depth of its concentration occurrence. The local low permeability lens in the porous medium caused of the pollutants blocked which will be accumulated on its surface and formed a pollution pool. The sensitivity analysis results demonstrated that the permeability coefficient was a key parameter to control the longitudinal migration speed and saturation distribution of LNAPL.

porous media；light non-aqueous phase fluid；multiphase flow；numerical simulation；parameter sensitivity analysis

X523

A

1000-6923(2021)04-1815-09

阮冬梅(1997-),四川绵阳人,吉林大学硕士研究生,主要从事水环境与水生态研究.

2020-08-25

国家重点研发计划(2018YFC1800400);国家自然科学基金青年基金资助项目(41807155);吉林省科技厅重点项目(20190303076SF)

* 责任作者, 教授, bianjianmin@126.com