成就目标定向与中学生数学学习投入的关系——数学焦虑的中介作用

屠西茜，杨新荣

1. 西南大学 数学与统计学院， 重庆 400715； 2. 西南大学 教师教育学院， 重庆 400715

数学课程改革的一个重要理念在于变革学生的数学学习体验， 如特别强调学生数学学习过程中的实践、 探索和合作交流等． 这些理念的实施， 也会影响学生数学学习过程中的投入程度． 学生学习投入被认为是促进学业成就的重要影响指标， 高投入水平的学生通常会表现出种种有利于学习的特征， 并取得更好的学业成绩[1-2]． 在先前学习投入研究中， 学习投入一般被界定为一个多维概念， 经典的学习投入主要包括行为、 情感和认知投入3个不同但相互关联的维度[3]． 但近来随着对学生学习过程中社会互动的倡导， 一些学者提出学习投入也应包含社会投入维度[4]． 总的来说， 数学学习投入是学习投入在数学学科的具体化， 是指学生在数学学习过程中积极参与数学课内外活动， 产生积极的情感， 有策略地学习， 并进行高质量的与数学学习相关的互动．

同时， 研究表明， 在中学阶段学生的数学学习投入呈下降趋势[5]． 因此， 系统探索数学学习投入的影响因素， 对于提升中学生的数学学习投入水平， 进而对提高中学阶段的数学教育质量具有重要的理论和实践意义． 已有研究表明在众多影响学生的学习投入因素中， 学习动机的作用最不容忽视． 学习动机作为一个个人的且不可观察的心理过程， 一般而言被认为是可观察学习行为的前因[6]． 本研究聚焦于学习动机中的一个重要变量——成就目标定向， 研究其对数学学习投入的影响机制， 以丰富对数学学科的学习动机与学习投入关系的理解． 一般而言， 成就目标定向通常被定义为参加任务的目的． Elliot 和Church将成就目标定向分为3个维度： 掌握定向、 表现-接近定向以及表现-回避定向[7]． 已有研究发现学生采用的目标定向与一系列的学习行为之间存在密切关联[8-9]． 趋近掌握定向的学生注重对学习内容的理解， 会促进积极的学术行为， 如付出更多精力， 与其他学生更积极讨论学业， 更多参与学校以外的相关活动， 并在需要时及时寻求帮助． 趋近表现-目标定向的学生主要在于证明自身的能力， 也有可能在学习中表现出一定程度的投入． 相反的， 选择表现-回避定向的学生则更专注于避免对自己不利的评价， 从而通常难以保持较高的学习投入水平．

此外， 在成就目标定向影响学生数学学习投入过程中是否还存在其他中介变量也是值得研究的重要问题． 在有关学习投入影响因素的研究中， 学业情绪是研究者广为关注的因素之一． 已有研究发现消极学业情绪会负面影响学生的学习投入[10]． 而数学焦虑作为一个关键的消极情感变量， 是阻碍学习和表现的主要因素[11]． 杜玉改等人[12]的研究结果表明， 考试焦虑与不同维度的学习投入均存在负向相关关系， 是学习投入的消极预测因素． 与此同时， 已有研究证实成就目标对学业焦虑也发挥着作用． Bandalos等人[13]发现考试焦虑和掌握定向之间存在负向关联， 和表现-接近定向之间存在正向关联． Daniels等人[14]的研究也得出了同样的结果． 此外， 刘惠军等人[15]对152名中学生进行的调查， 证明了表现-回避定向对考试焦虑的促进作用．

综合上述研究可以看出， 成就目标定向、 数学焦虑、 数学学习投入是3个相互密切关联的变量． 但是针对中学生这一特定群体， 还鲜有研究探索数学焦虑是否在成就目标定向与数学学习投入之间发挥着中介作用． 因此， 为了更深入了解这3个变量之间的关系， 本研究以不同年龄和不同教育水平的中学生为研究对象， 探讨数学焦虑在成就目标定向对数学学习投入的中介作用． 本研究做出如下几个初步假设： ① 数学焦虑对数学学习投入存在负向影响； ② 表现-接近定向和掌握定向对数学学习投入均有正向的直接影响， 而表现-回避定向对数学学习投入有负向的直接影响； ③ 数学焦虑在成就目标定向和学习投入之间发挥中介作用．

1 研究方法

本研究采用匿名调查的方法， 打乱问卷题项的顺序， 部分题项采用反向计分． 将有效问卷随机分成两组， 通过探索性因素分析(EFA)和验证性因素分析(CFA)进行问卷质量分析． 其中， CFA拟合指标包括： 卡方拟合优度检验指标χ2/df， 近似误差的均方根RMSEA， 比较拟合指数CFI， Tucker-Lewis指数TLI， 以及标准化残差均方根SRMR． 在完成问卷的最终版本之后， 对最终版本问卷的数据进行进一步分析， 以探索变量之间的结构关系．

1.1 样 本

本研究选取广西、 河南、 四川、 湖北及重庆市的8所中学， 采取整群抽样法分别抽取初一、 初二、 高一、 高二的学生发放问卷进行调查． 共发放问卷1800份， 回收有效问卷1466份， 有效回收率为81.444%． 其中男生621人， 女生833人， 12人缺失性别信息． 初一336人， 初二324人， 高一405人， 高二392人， 9人缺失年级信息． 944人居住在城市， 501人居住在农村， 21人缺失居住地信息．

1.2 测量工具

1.2.1 数学学习投入问卷

采用Fredricks等人编制的数学学习投入问卷[16]， 该问卷将数学学习投入分为行为投入、 情感投入、 认知投入以及社会投入4个维度， 问卷使用Likert 5 点计分(1=完全不符合， 5=完全符合)． 经EFA发现一些项目因子载荷非常小， 有些项目存在严重的交叉因子载荷， 删除这些项目组成最终的正式数学学习投入问卷． 最终数学学习投入问卷共包含22题， 其中行为投入维度6题， 情感投入维度6题， 认知投入维度5题， 社会投入5题， 4个子维度共解释总方差的62.967%． 该问卷的CFA结果表示问卷具有良好的拟合度(χ2/df=4.084，RMSEA=0.064，CFI=0.928，TLI=0.918，SRMR=0.045)． 各维度的Cronbach’sα系数分别为0.847， 0.889， 0.801和0.878， 总问卷的Cronbach’sα系数为0.937．

1.2.2 成就目标定向问卷

对中学生采用成就目标定向问卷进行成就目标的测量， 该问卷由表现-接近定向、 表现-回避定向和掌握定向3个维度组成， 采用Likert 5点计分法(1=完全不符合， 5=完全符合)[8]． 每个维度6个题项， 问卷一共18个题项． 经EFA删除载荷量较小的题项， 最终正式问卷共保留14个项目． 3个因子解释总方差的54.565%． CFA结果显示问卷具有较高的拟合度(χ2/df=3.695，RMSEA=0.060，CFI=0.936，TLI=0.921，SRMR=0.043)． 各维度的Cronbach’sα系数分别为0.763， 0.805和0.569， 总问卷的Cronbach’sα系数为0.699．

1.2.3 数学学习焦虑问卷

采用Bai等人编制的数学焦虑问卷[17]． 通过改编保留单一维度， 问卷采用 Likert 5 点计分法(1=完全不符合， 5=完全符合)． EFA结果解释总方差的71.477%， 最终形成的问卷共5个题项． CFA显示各拟合指标均在可接受范围内(χ2/df=1.939，RMSEA=0.035，CFI=0.998，TLI=0.995，SRMR=0.010)． 问卷的Cronbach’sα系数为0.894．

2 研究结果

2.1 共同方法偏差检验

采用Harman 单因素检验的方法检验共同方法偏差， 采用 SPSS进行因素分析， 结果显示未旋转的因素分析得到7个因子， 第一个因子解释方差变异为32.981%， 小于40%的标准[18]， 表明不存在严重的共同方法偏差．

2.2 数学学习投入描述性统计和差异检验

表1中的N为每个维度的项目数，M和SD为每个维度所有题项的平均值和标准差． 结果显示学习投入4个维度得分最高的是行为投入(M=3.753)， 其次是情感投入(M=3.523)、 社会投入(M=3.094)， 这3个维度的平均数大于中位数3， 表明中学生的行为投入、 情感投入以及认知投入水平良好． 得分最低的维度是认知投入(M=2.794)， 表明与其他维度相比， 中学生的认知投入水平较低． 数学焦虑维度平均分为2.577， 表明学生数学焦虑水平较低． 对于成就目标定向的3个维度， 掌握定向维度平均分最高(M=3.926)， 表明学生偏向于持有掌握定向的数学成就目标． 随后将所有子维度得分与理论中值3进行单因素t检验， 结果表明除认知投入、 数学焦虑以及表现-回避定向得分显著低于中值3之外， 行为投入、 情感投入、 社会投入、 表现-接近定向及掌握定向得分均显著高于3， 处于中等偏上水平．

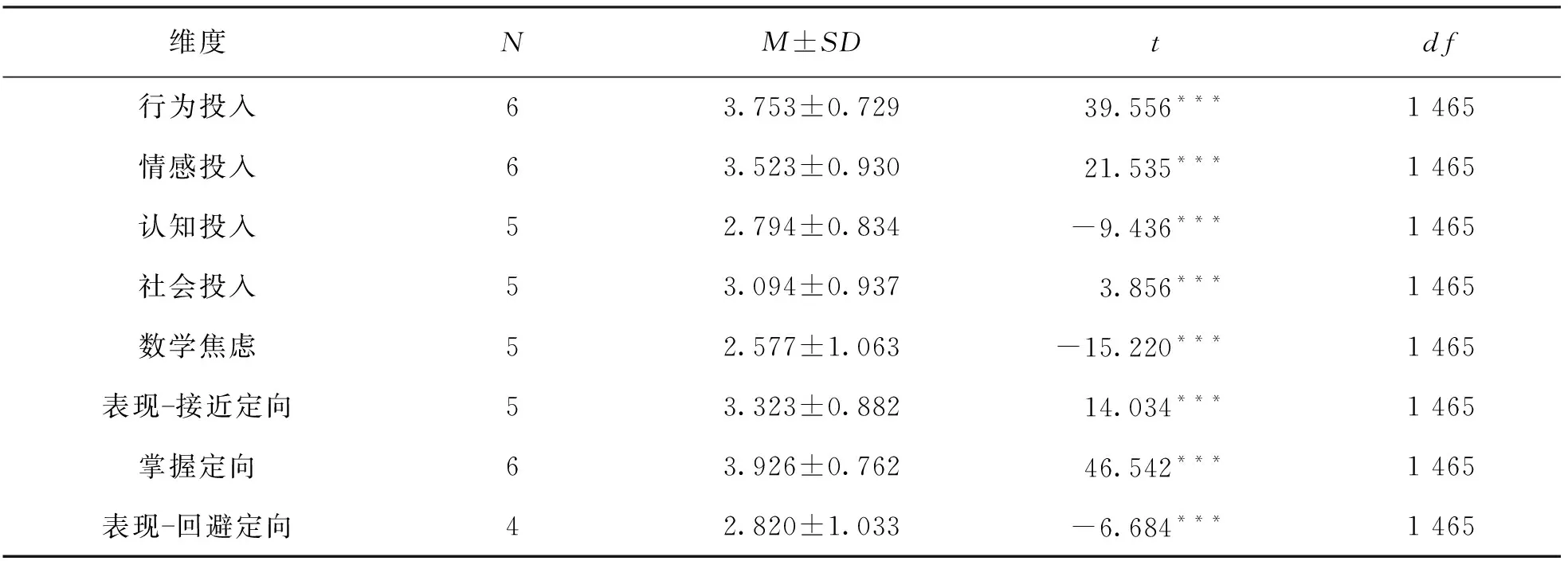
表1 描述性统计

此外， 本研究采用独立样本t检验对所调查学生分性别、 年级和地域进行了学习投入水平的差异检验， 结果如表2所示． 由结果可以看出， 行为投入及社会投入性别差异无统计学意义， 而情感投入和认知投入性别差异有统计学意义． 初中阶段和高中阶段在4种学习投入维度上得分差异有统计学意义． 总的来说， 初中阶段得分均高于高中阶段； 不同居住地学生在各维度上得分差异有统计学意义； 城市学生数学学习投入水平显著高于农村学生．

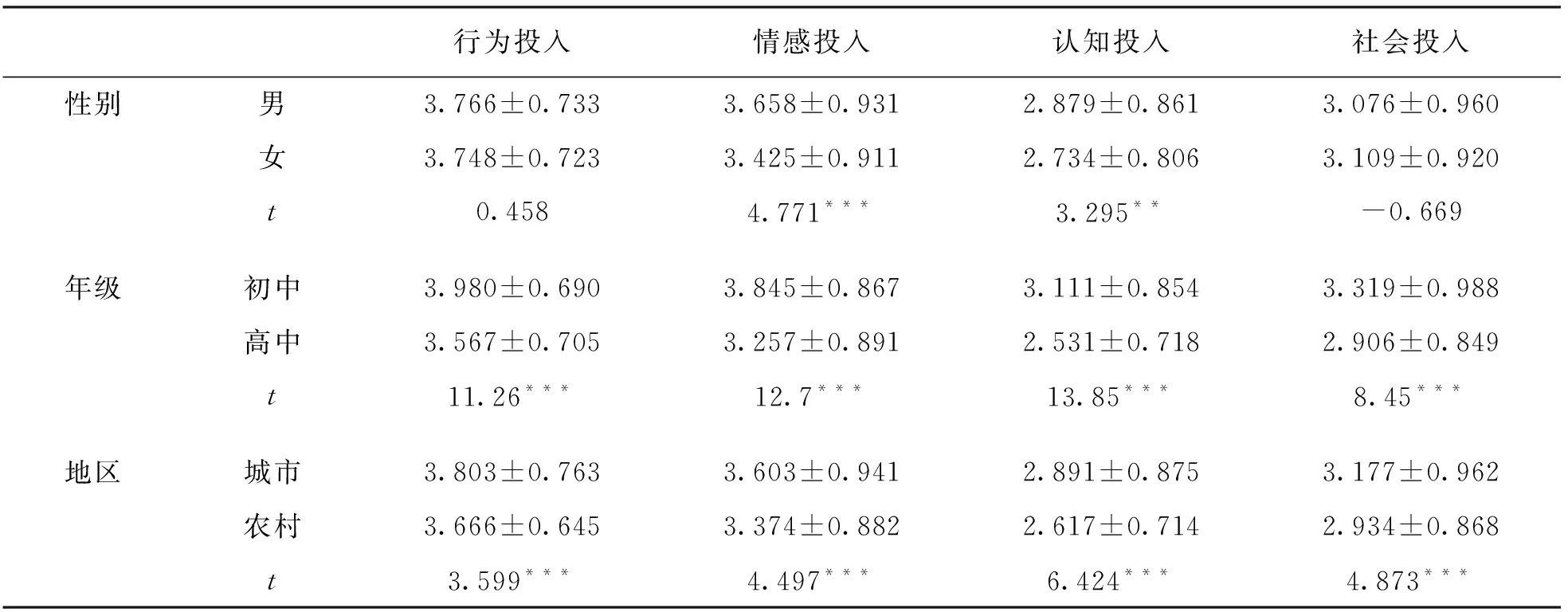
表2 中学生学习投入在人口学变量上的平均数差异检验(M±SD)

2.3 相关分析

表3展示了在控制性别、 年级和居住地之后各个变量两两之间的相关以及显著性． 结果表明学习投入的4个维度均与学业焦虑呈负相关， 与掌握定向及表现-接近定向均呈正向相关， 而与表现-回避定向呈负向相关． 同时， 相关分析表明学业焦虑与掌握定向及表现-接近定向均呈负向相关， 与表现-回避定向呈正向相关．

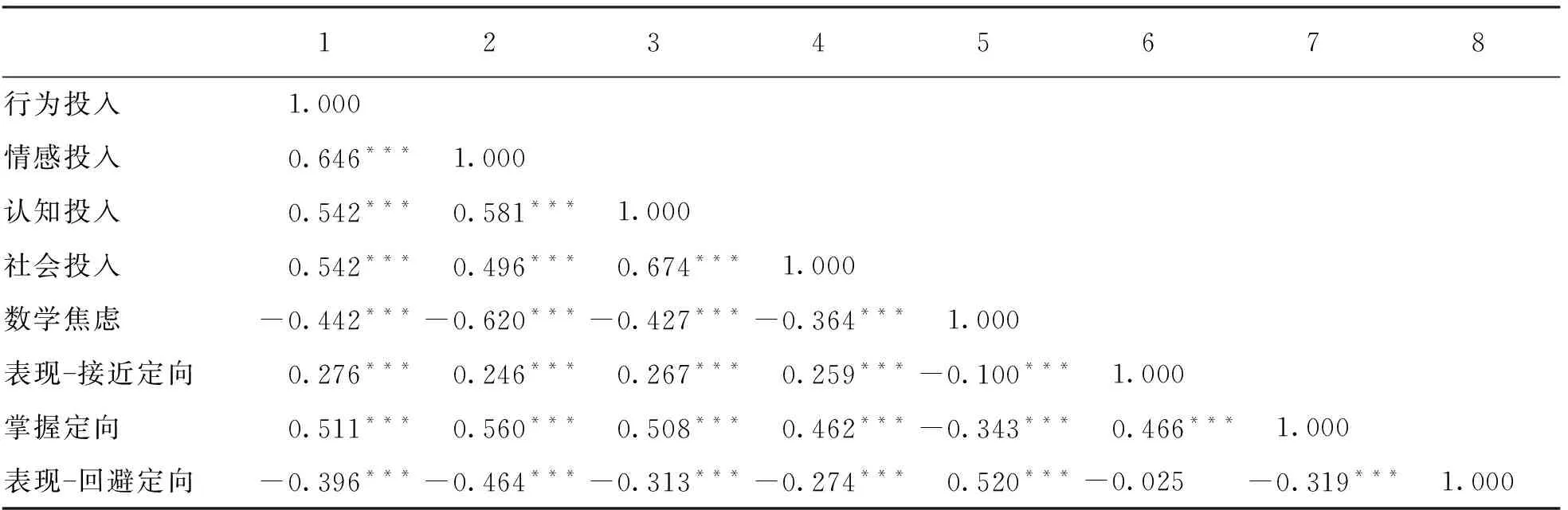
表3 相关分析

2.4 数学焦虑的中介作用

本研究采用潜变量结构方程模型考察成就目标定向、 数学焦虑对数学学习投入的影响． 采用Bootstrap法进行中介效应检验， 首先从总体中进行有放回的重复抽样得到Bootstrap样本， 重复1 000次得到1 000个Bootstrap样本， 进而得到1 000个中介效应的估计值， 根据95%的置信区间进行检验： 若95%置信区间不包含0， 则认为中介效应存在； 置信区间包括0， 则中介效应不存在[19]． 图1展示了数学焦虑在表现-接近定向与数学学习投入之间的中介作用． 模型的拟合指标为：χ2/df=5.675，RMSEA=0.056，CFI=0.913，TLI=0.906，SRMR=0.058． 结果发现表现-接近定向可以直接预测数学学习投入(β=0.284)， 也可以通过数学焦虑的中介作用对数学学习投入产生间接影响． 数学焦虑的中介效应为0.099， 间接效应对应的95%的Bootstrap置信区间为[0.053， 0.148]， 置信区间不包含0， 效应显著．

图2为数学焦虑在掌握定向与数学学习投入之间的中介作用模型． 模型的拟合指数为：χ2/df=5.800，RMSEA=0.057，CFI=0.910，TLI=0.903，SRMR=0.055． 结果表明掌握定向可以直接预测数学学习投入(β=0.538)， 也可以通过数学焦虑的中介作用对数学学习投入产生间接影响． 数学焦虑的中介效应为0.212， 间接效应对应的95%的Bootstrap置信区间为[0.180， 0.250]， 置信区间不包含0， 效应显著．

a1～a5分别代表数学焦虑的5个条目； b1～b5分别代表表现-接近定向的5个条目； *** p<0.001．图1 表现接近定向与数学学习投入的中介模型

a1～a5分别代表数学焦虑的5个条目； c1～c6分别代表掌握定向的6个条目； *** p<0.001．图2 掌握定向与数学学习投入的中介模型

以表现-回避定向为自变量， 建立数学焦虑在表现-回避定向与数学学习投入之间的中介模型， 结果如图3所示． 模型的拟合指数为：χ2/df=6.190，RMSEA=0.060，CFI=0.916，TLI=0.908，SRMR=0.055． 结果表明表现-回避定向对数学学习投入的直接作用不显著， 而是通过数数学焦虑的完全中介作用对数学学习投入产生间接影响． 数学焦虑的中介效应为-0.227， 间接效应对应的95%的Bootstrap置信区间为[-0.320， -0.160]．

a1～a5分别代表数学焦虑的5个条目； d1～d3分别代表表现-回避定向的3个条目； *** p<0.001．图3 表现回避定向与数学学习投入的中介模型

3 讨 论

3.1 中学生数学学习投入、 数学焦虑以及成就目标定向的现状

本研究以中学生作为研究对象， 对数学学习投入、 数学焦虑以及成就目标定向的现状作了分析． 描述性统计结果表明， 对于数学学习投入， 除认知投入以外， 行为、 情感和社会投入均高于理论中值3， 属于中等偏上水平． 说明现阶段中学生对于数学学习普遍能够保持积极的态度和情感， 能积极参加各种数学学习任务， 并与同学有较高水平的数学互动． 值得注意的是， 本研究发现中学生数学认知投入水平偏低． 这可能是由于中学阶段数学难度比小学阶段明显增加， 一部分学生适应困难， 从而降低了数学认知投入． 另外本研究发现学生的数学焦虑得分低于中值3， 处于中等偏下水平． 由于本次调查未针对毕业年级， 可能这些学生还没有过重的升学压力， 由此在数学学习过程中， 并没有表现出过大的心理负担， 从而导致数学焦虑． 在成就目标定向方面， 中学生的表现-接近定向和掌握定向均处于中等偏上水平， 而表现-回避定向属于较低水平． 这反映出在中学生数学学习过程中， 大多数学生以掌握数学学习内容和表现出更高的数学能力水平为目标．

另外， 本研究结果表明数学情感和认知投入2个维度上的性别差异有统计学意义， 男生得分显著高于女生， 这可能由于男生和女生受到的社会期望不同造成的． 一般而言男生普遍承担更高的家庭期许， 为了提高自身的竞争力， 男生往往会对数学学习投入更多的情感， 从而采用更为深层次的学习策略． 由此中学阶段数学教学可以使用差异教学， 更加注重女生数学态度的培养， 缩小男女生在数学上的学习投入差异．

此外， 本研究还发现4种学习投入年级差异有统计学意义． 总的来说， 初中学生普遍比高中学生拥有更高水平的数学学习投入． 刘在花[20]的研究也发现随着年级升高， 学生对学习的态度也会逐渐发生变化． 从初中到高中， 学生面临的数学学习压力日益增加． 特别在高中阶段， 学生的学习时间和学习强度都在不断提高， 而这种外界压力在很大程度上会降低学生的内在学习动机， 从而导致学习投入表现出下降的趋势． 因此， 对于高中学生， 日常教学更应该给予学生一定的自主性， 培养学生的数学学习效率而不是长时间的机械练习和高强度的学习． 同时， 本研究还发现数学学习投入城乡差异有统计学意义． 总的来说， 对于本研究调查样本而言， 城市学生的数学学习投入水平普遍高于农村学生投入水平． 这可能是由于城市学校的教学条件、 师资水平和家长对数学学习的重视程度都要高于农村， 从而使得城市学生在数学学习的投入程度上也相应地高于农村学生．

3.2 成就目标定向与数学学习投入的关系

本研究发现不同类型的成就目标定向与数学学习投入之间的关系不同． 表现-接近定向和掌握定向与数学学习投入均正相关有统计学意义． 具体而言， 中学生的表现-接近及掌握定向越强， 则在数学学习中会表现得更投入． 当学生专注于掌握数学内容时， 他们往往愿意更为深入地思考数学问题， 愿意使用有效的数学学习和自我监管策略， 自我调节产生更为积极的数学学习情感， 也会更倾向于跟同学进行数学学习方面的交流和讨论， 从而提升其数学学习投入水平． 这也说明表现-接近定向与使用认知策略有关， 与消极情感存在负向关系， 进而正向影响数学学习投入． 这一结果也与已有的研究结果一致[21-22]．

不过倾向于持有表现-接近定向的学生与倾向于持有掌握定向的学生在一定程度上存在区别． 从本研究结果可以明显看出与表现-接近定向相比， 掌握定向能预测更高的数学学习投入水平． 也就是当学生追求掌握定向时， 他们的目标是真正学习或掌握数学任务， 学生会主动参加多种类型的数学学习活动． 相反， 当学生追求表现-接近定向时， 目标是展示自身在进行数学任务的能力， 避免在任务中表现出无能． 当学生持有这样的学习目标时， 他们的学习投入也就可能不如掌握定向那么深， 但在一定程度上也会促使他们付出努力和精力来进行数学学习． 此外， 如果学生对他们超越他人的机会感到悲观， 他们就可能会采取表现-回避定向． 也就是由于他们恐惧失败， 就会进一步减少数学投入， 由此来避免使自己看起来缺乏能力．

3.3 数学焦虑在成就目标定向与数学学习投入之间的中介作用

本研究通过结构方程模型探索数学焦虑在成就目标定向与中学生数学学习投入之间的中介作用． 研究结果显示数学焦虑在表现-接近定向、 掌握定向以及表现-回避定向与数学学习投入的关系之间均发挥显著的中介作用． 若中学生拥有较强的掌握定向和表现-接近定向， 会在一定程度上减少学生的数学焦虑水平． 相反， 若中学生持有表现-回避定向， 则会增加学生的数学焦虑水平． 而高水平的数学焦虑往往对学习过程产生负面影响， 降低学生的数学学习投入水平． 这与很多先前关于成就目标和学业焦虑的研究结论类似[23-24]． 这也可能由于趋于掌握定向和表现-接近定向的学生注意力集中在掌握数学任务和表现自身的数学能力上， 愿意为了实现个人目标付出努力． 因此， 在数学学习过程中会主动调整自己的数学学习策略， 调节自身的负面情绪． 而趋于表现-回避定向的学生渴望获得良好的表现， 想向他人展示自己的能力， 过于关注外在的判断或排名， 很容易受到外界的干扰， 从而导致负面情感的产生． 因此， 对于数学焦虑水平较高的低数学学习投入的学生， 如果仅仅对其数学焦虑水平进行干预， 只通过减少其数学焦虑程度来提高数学学习投入可能不会有太大的效益． 而将数学焦虑的干预措施与树立积极的成就目标定向相结合可能会取得更为优良的效果．

总的来说， 本研究结果证实了数学焦虑在成就目标定向对数学学习投入的影响中起着关键的作用． 因此在实践中， 理应更关注并对此问题进行干预， 帮助学生建构积极的数学学习动机． 同时要重视学生的数学学习过程而不是只关注数学学习成果及表现， 激发学生的数学学习兴趣， 培养学生的学习积极性和内在动机． 此外， 还要引导学生树立正确的数学成就目标， 不要过多地关注学生之间的比较， 而应把关注点放在个人的进步上， 降低学生的数学焦虑， 尽量减少数学学习非投入现象的产生．

4 结 论

1) 中学生数学学习投入普遍处于中等偏高水平， 且存在性别、 年级及城乡差异．

2) 表现-接近定向和掌握定向对于中学生的数学学习投入存在显著的正向预测作用， 而表现-回避定向对中学生数学学习投入的预测作用无统计学意义．

3) 在成就目标对学习投入的预测作用中， 数学焦虑起到中介作用． 其中， 在掌握定向和表现-接近定向对于学习投入的影响中起正向中介作用， 在表现-回避定向对学习投入的影响中起负向中介作用．