结合局部全局一致性和支持向量机的半监督分类方法

池辛格，王立国

哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001

遥感技术是近代发展起来的一种综合的对地观测技术。其定义是通过某种设备，不接触被测目标或区域来获取相关数据，并对其进行分析从而得到所需要信息[1]。遥感界根据光谱分辨率将成像光谱技术划分为多光谱遥感、高光谱遥感和超光谱遥感3类[2]。其中，高光谱遥感(hyperspectral remote sensing, HRS)技术作为遥感领域的前沿技术，通过融合目标探测和光谱成像技术，能够表征地物的多维特征信息，实现更详细的地物分类，受到了广大研究者的青睐，并被广泛应用于军事、农业、林业、畜牧业等领域，为我们的生活和工作带来了便利[3]。与传统的遥感技术相比，高光谱遥感能够获得更加丰富的光谱特征并有效反映特征间的细微差异，通过地物的数百个连续的谱段信息提供丰富的光谱信息[1]。高光谱遥感的特点也为处理技术带来了新的挑战。在高光谱图像的分类方向，庞大高维的数据和相互重叠的众多波段往往会导致维数灾难现象，获得准确地物标签的极高代价使得有标签样本数量极少，且不一定具有代表性，这些问题对高光谱图像的分类产生了极大的影响。

如今较为常用的高光谱分类方法有无监督分类、监督分类和半监督分类几种。常用的监督分类方法包括最大似然算法[4]、支持向量机(support vector machine, SVM)和人工神经网络等。此类方法依赖于先验知识的获取来进行分类，因此需要大量标记准确的训练样本。当训练样本数量过少或代表性不够强时，分类效果不佳。同时高光谱数据中大量的准确标记也带来了成本过高的问题。常用的半监督分类方法有半监督支持向量机[5]、基于图的半监督算法[6]和协同训练(Cotraining)[7]等。此种分类方法不仅利用了先验信息，还能充分挖掘无标签数据中的信息，弥补了另外两种分类方法的不足，有效地提高了分类精度。

在监督分类算法中，支持向量机(support vector machine, SVM)于1995年由Vapnik等提出[8]，该方法以统计学习理论中的VC维(vapnik chervonenks dimension)准则和结构化风险最小化准则(structural risk minimization inductive principle)作为理论依据，寻找能将两种样本进行最佳分类的超平面，在处理高维非线性数据方面有极大的优势，分类器的泛化性能和推广性很强，这些优势使在高光谱图像分类中得到广泛应用。

在半监督分类方法中，基于图的半监督算法因其设定参数少，过程较为直观等优点被研究者所青睐。基于图的半监督算法最早由Blum A等[7]提出，此种方法以每个样本点作为节点，样本点间的相似程度作为连接两个节点的边，将数据集构造为一个图，以此挖掘无标签样本的信息。根据所有的节点是否两两相连可以分为全连接图和近邻图，根据边有无方向可以分为有向图和无向图。常见的基于图的半监督分类算法有标签传递算法[9]，高斯随机场算法和流形正则化算法等。

经典的标签传递算法由于传递过程中的随机性，分类精度和稳定性较差，无法在实际中应用，传统的SVM算法被监督分类方法本身的缺陷限制，受样本选择的影响极大，针对两种算法的缺陷，本文提出了一种结合局部和全局一致性（learning with local and global consistency，LLGC）算法和SVM算法的半监督分类方法，通过筛选2种算法对无标签训练样本分类结果相同的样本并加入有标签训练样本集辅助分类，用扩充后的训练样本训练SVM分类器预测测试样本。在Indian Pines和Paiva两个数据集的实验中证明了算法的有效性

1 支持向量机

支持向量机分类方法的基本思想是寻找一个可以最大程度正确地将2类样本划分在两侧的超平面，即最优超平面，保证每类样本中与超平面距离最近的样本与超平面之间的距离最大[10]，其本质是一种二分类算法。如今SVM理论由于其在处理高维非线性数据方面的优势，已经成为高光谱分类领域应用最广、适应性最强的监督分类算法，在模式识别、机器学习等问题中也作为主流算法大量出现。

设n维空间中存在样本集(x1,y1),(x2,y2),···,(xl,yl)，其 中xi∈Rd，样 本 的类别yi∈{−1,+1}，样本数目为l。SVM的目标是找到超平面wTx+b=0 ，其中w=[w1,w2,···,wn]T为权向量，b是常数。当样本线性可分时如图1所示。

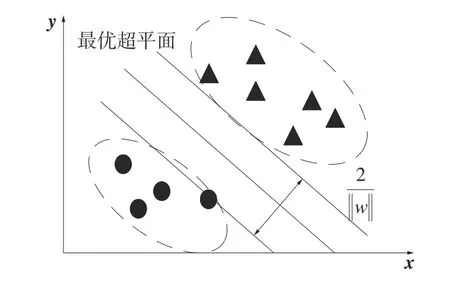
图1 线性可分情况下最优分类面

此时2个类别的支持向量到最优分类超平面的距离之和，可以表示为这就是2个类别间的几何间隔。SVM中需要使类别间的几何间隔最大，等价于使‖w‖最小，于是寻找最优分类超平面的问题转化为如下优化问题[11]：

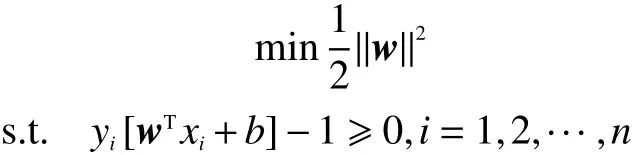
其中αi是拉格朗日乘子，且αi≥0，i=1,2,···,n。

对w和b求偏导后带入拉格朗日函数，即可得到对偶问题。此时优化问题已经转化为最大化如下目标函数：

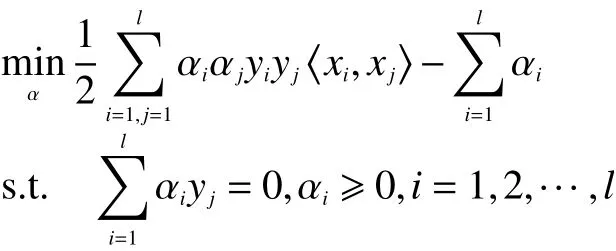
可以求得：

最终得到相应的判别函数式为

这种对于线性可分的样本集的间隔最大化过程被称为“硬间隔最大化”。

在有些情况下训练集中会出现一些异常的样本点，导致训练集线性不可分。线性不可分样本集的近似分类如图2所示。

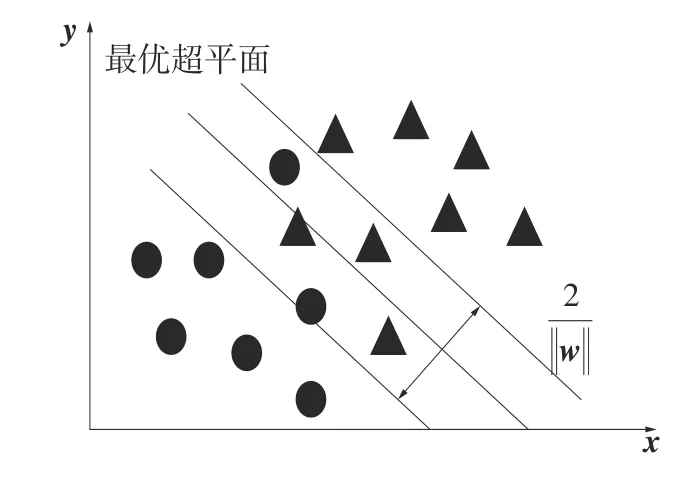
图2 线性不可分样本集的近似分类

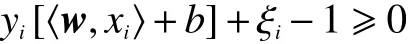
此时可将约束条件放宽为代表允许某些异常点被分到错误的类中，同时引入松弛变量的惩罚项C以实现最小化错分程度和最大化目标间隔。此时原始问题可以描述为

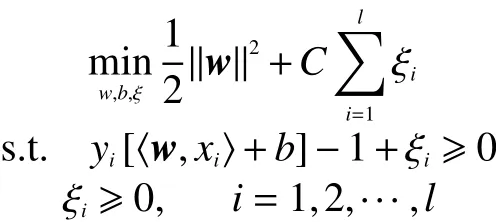
对于式(1)～(9)，可以采用同样的求解方法，可得到最终结果：

这种通过修正目标函数实现间隔最大化的过程被称为“软间隔最大化”。

在实际应用中往往会遇到非线性的分类问题，此时应将原本的样本空间Rd映射到一个高维的希尔伯特空间H使样本集线性可分或近似线性可分，此后即可使用硬间隔最大化或软间隔最大化对样本进行分类。

假设函数φ是一个从低维特征空间到高维特征空间的映射,那么在非线性分类过程中内积应该被替换为

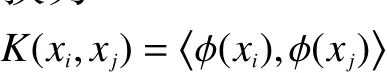
称K(xi,xj)为核函数(kernel function)。此时目标函数变为

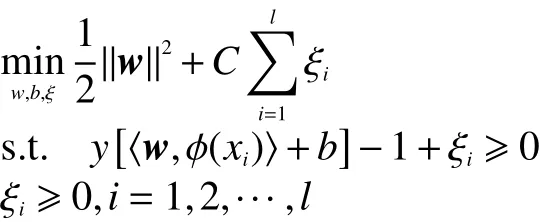
相应的判别函数式为

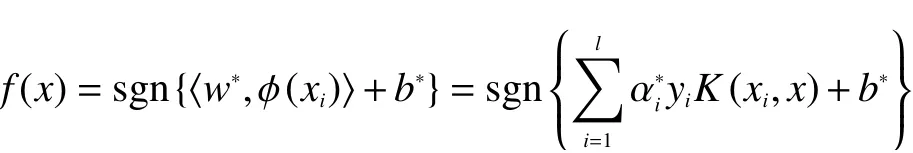
常见的核函数有线性核、多项式核、拉普拉斯核、径向基函数核等。

2 局部全局一致性算法

LLGC方法的原理就是通过局部和全局一致性假设来定义能量函数。依据相邻的样本点可能属于同一类别传递标签信息，使能量函数取最小值，为不带标签样本点进行标注，得到分类结果。同其他基于图的分类方法类似，LLGC包含3个部分：1)构造一个包含所有样本的无向图；2)求解相似度矩阵W；3)定义恰当的能量函数以评价算法。能量函数是描述整个系统状态的测度，也是评价算法性能的重要指标。能量函数一般由损失函数和正则化项组成，其表达式为

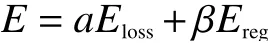
式中α、β为正则化参数，损失函数用于保证得到的类别标签尽可能接近真实标签，正则化项可以保证图的局部平滑，即保证特征相似的样本得到相同的标签。在LLGC中，最小化能量函数能够得到最佳的分类结果。由于LLGC算法在本质上是一种标签传递算法，所以其主要思想是通过无穷次迭代将有标签样本的信息传递给特征相似的近邻样本[12]，最终达到全局稳定状态。LLGC算法的具体步骤为

1)构造一个包含全部样本的无向图，建立图的邻接矩阵W。为防止样本点将自身标签不断传递给自身，当i≠j时 ，W=exp(−(x−x)2/2σ2)，其中ijij σ为常数；当i=j时 ，Wii=0。

2)通过邻接矩阵W得到概率传播矩阵S=D−1/2WD−1/2，其中D是一个对角矩阵，对角线元素

3)对概率矩阵F(0)进行初始化标注，使F(0)=Y；样本间开始传递标签，按照如下公式更新每个样本点标签的概率分布：F(t+1)=αSF(t)+(1−α)Y，不断迭代直至收敛。

4)设F∗为 {F(t)}在t趋于正无穷时的极限，那么可以得到样本点xi的标签表达式：

步骤3)中的Y矩阵为全部样本的标签信息，假设某样本点xi属于第j类，那么该样本点对应的类别标签为yij=1，第i行的其他位置和无标签样本对应的位置处均为0。

3 本文算法

在半监督分类方法中，扩充训练样本集可以有效地解决有标签样本数量有限的问题，如自训练方法和协同训练方法。本文受协同训练启发，提出了一种结合LLGC和SVM的半监督分类算法LL_SVM。LLGC算法在标签的传递过程中的随机性导致了分类精度不理想、分类结果不稳定的缺陷，SVM是监督分类方法，在样本较少的情况下，分类精度不理想，最终的分类结果与样本的选择关系较大。由于样本是随机选择的，不一定具有代表性，因此SVM的分类结果也不稳定。本章算法利用基于图的分类方法与支持向量机方法结合，通过两种分类器共同筛选具有代表性和类别确定的样本，尽可能改善二者初始性能较弱的问题，充分挖掘未标记样本中蕴藏的信息，辅助少量的已标记样本得到性能良好的分类器。具体实验步骤如下。

输入带标签训练样本集Dl={(x1,y1),(x2,y2),···,(xl,yl)} ，无标签样本集U={xl+1,xl+2,···,xn},其中整体训练样本集 χ=Dl∪U，类别标记矩阵Y。

1)使用Dl进行SVM分类器训练，获得分类器HSVM；

2)使用分类器HSVM对U中的无标签样本类别进行预测，得到预测标签LSVM；

3)基于样本集χ，计算所有样本之间的相似度，获得样本的邻接矩阵W；

4)基于样本标记矩阵Y，使用LLGC算法预测样本集U中未标记样本的类别，得到预测标签LLLGC；

5)保留预测标签一致的样本，加入到已标记样本集Dl，训练SVM分类器；

6)使用该分类器对测试样本进行分类，对算法进行评价。

输出测试样本的预测标签和评价指标。

算法的流程图如图3所示。

图3 LLGC_SVM算法流程

4 实验结果与分析

4.1 实验数据

实验采用2个经典的高光谱数据集进行仿真：1992年夏季在美国西北部印第安纳州农林混合实验场拍摄的AVIRIS高光谱图像数据集的一部分和应用成像光谱仪在帕维亚大学上空获得的Pavia高光谱数据集。两图像的大小均为像素，其中AVIRIS高光谱图像的光谱值区间大约在0.41～2.45 μm，空间分辨率为20 m，光谱分辨率为10 nm，图像的原始波段为220个，去除信噪比较低和不能被水反射的20个波段后实际参与图像处理的波段共200个。其监督图像如图4(a)所示。Pavia高光谱图像光谱值区间大约在0.43～0.86 μm，空间分辨率为1.3 m，原始波段为115个，去除15个噪声波段后实际参与图像处理的波段共103个。其监督图像如图4(b)所示。

图4 实验数据集示意

4.2 实验环境

实验仿真条件：电脑处理器为Intel(R) Core(TM) i7-2630QM，6G RAM，64位windows10操作系统，MATLAB软件版本为matlab2019b。每次实验进行10次取平均值作为实验结果。

4.3 评价准则

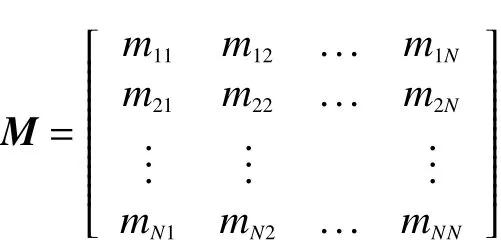
混淆矩阵(confusion matrix)是表示高光谱图像分类精度的一种标准格式，其具体表现形式为式中：mij(i=1,2,…,N,j=1,2,…,N)表示第i类样本被错分为第j类的总像元个数；N为所有类别的总个数。mii(i=1,2,…,N)为被准确划分类所属类别的像元数，mii越大则说明分类精度越高[13]。通过混淆矩阵可以得到3个评价指标：总体分类精度(overall accuracy，OA)，平均分类精度(average accuracy，AA)和Kappa系数。

假设N为总的类别数，n为样本总数，mii为第i类分类正确的样本数，mi+表示第i行的所有m值求和。则总体分类精度OA的计算方法为

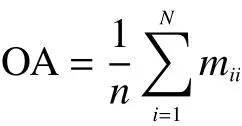
平均分类精度AA的计算方法为

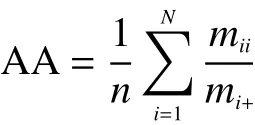
Kappa系数的计算方法为

OA、AA和Kappa系数越大，说明分类效果越好。

4.4 实验结果和分析

为了验证本文所提方法的有效性，在印第安农林和帕维亚大学这两个高光谱据集上进行仿真，总共对4种算法进行了对比，包括经典的SVM算法，经典的LLGC算法，文献[14]中提出的KNN_LLGC算法和本文提出的结合LLGC和SVM的半监督分类算法LL_SVM算法。KNN_LLGC算法首先选取训练样本的近邻标签，然后通过对比KNN算法确定的近邻标签和LLGC算法确定的近邻标签，取出预测结果相同样本并加入训练集，然后使用LS-SVM分类器对测试样本进行分类，算法中的近邻数目取20个。标准SVM采用径向基核函数，采用“one-againest-rest”多分类算法，惩罚因子C以及核参数σ通过网格搜索法在[10, 103] 和 [10-2, 102]中选取最优值。LLGC算法中的参数α以及对比实验中的高斯核宽度σ设定为 α=0.99， σ=0.11，迭代次数为5次。

表1为4种算法在Indian Pines数据集分类中的性能对比，评价标准为OA、AA和Kappa系数。实验选取总样本中的10%作为训练样本，其余为测试样本，每类训练样本中选取10个作为有标签训练样本，用于模拟小样本的实验条件。图5显示了4种方法的分类结果。

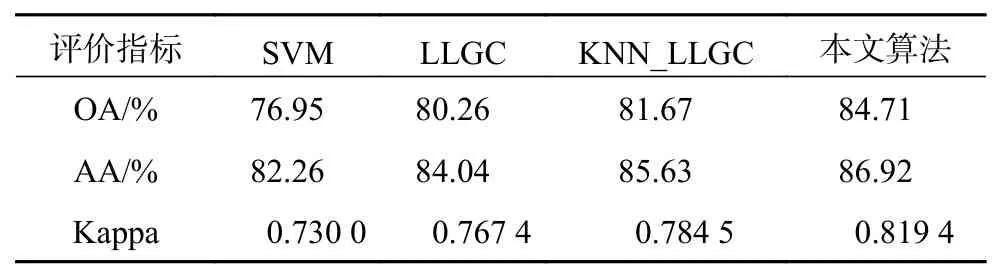
表1 Indian Pines高光谱图像分类结果

图5 Indian Pines数据集分类结果

从表1可以看出，在该数据集上，KNN_LLGC算法相对于传统SVM算法的总体分类精度提高了4.72%，均分类精度提高了3.37%，Kappa系数提高了0.054 5，相对于传统LLGC算法总体分类精度提高了1.41%，平均分类精度提高了1.59%，Kappa系数提高了0.017 1。本文提出的算法相对于KNN_LLGC算法效果有了极大的提升，总体分类精度提高了3.04%，平均分类精度提高了1.29%，Kappa系数提高了0.034 9，证明了在该数据集上本文算法的有效性。

从表2可以看出，传统LLGC算法在小样本条件下的分类精度很不稳定，传统SVM算法3种评价指标的波动幅度相对于LLGC算法较小，在与KNN算法结合后总体分类精度的波动幅度相对SVM提高了0.11%，相对LLGC算法降低了1.3%；平均分类精度的波动幅度相对于SVM提高了0.51%，相对于LLGC算法降低了0.55%；Kappa系数的波动幅度相对于LLGC算法降低了0.159。本文提出的算法对比KNN_LLGC算法，总体分类精度的波动幅度降低了1.73%，平均分类精度的波动幅度降低了1.39%，Kappa系数的波动幅度降低了0.019 7。上述数据证明了在该数据集上本章算法对于分类稳定性的提升效果。

表2 Indian Pines数据集分类结果的波动幅度

表3为上述4种算法在Pavia数据集分类中的性能对比，评价标准为OA、AA和Kappa系数。实验依然选取总样本中的10%作为训练样本，每类训练样本中选取10个作为有标签训练样本。图6显示了4种方法的分类结果。

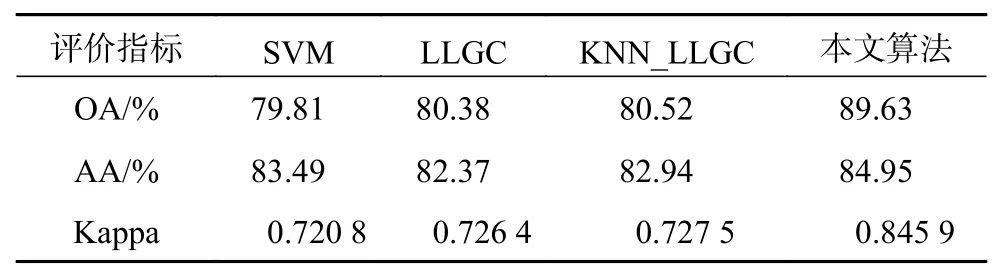
表3 Pavia高光谱图像分类结果

从表3可以看出，在该数据集上，KNN_LLGC算法相对于传统SVM算法的总体分类精度提高了0.71%，Kappa系数提高了0.006 7，相对于传统LLGC算法总体分类精度提高了0.14%，平均分类精度提高了0.57%，Kappa系数提高了0.001 1。本文提出的算法相对于KNN_LLGC算法效果有了极大的提升，总体分类精度提高了9.11%，平均分类精度提高了2.01%，Kappa系数提高了0.118 4，证明了在该数据集上本文算法的有效性。

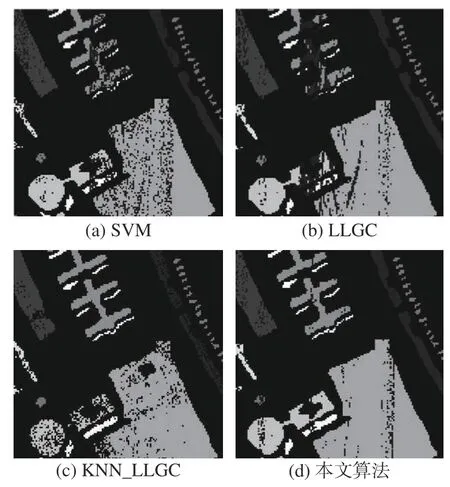
图6 Pavia数据集分类结果

通过上述两组实验能够证明本文算法在不同数据集上的适应性。在Indian Pines数据集和Pavia数据集上，本文采用的MCLU采样策略和改进的自适应参数对高光谱图像的分类精度相比于传统算法有较大的提升。

从表4可以看出，传统SVM和LLGC算法在小样本条件下的分类精度很不稳定，在与KNN算法结合后总体分类精度的波动幅度相对于SVM降低了5.31%，相对于LLGC算法降低了2.71%；平均分类精度的波动幅度相对于SVM降低了1.48%，相对于LLGC算法降低了2.1%；Kappa系数的波动幅度相对于SVM降低了0.063，相对于LLGC算法降低了0.325。本文提出的算法对比KNN_LLGC算法，总体分类精度的波动幅度降低了4.82%，Kappa系数的波动幅度降低了0.049 3。上述数据证明了在该数据集上本文算法对于分类稳定性的提升效果。

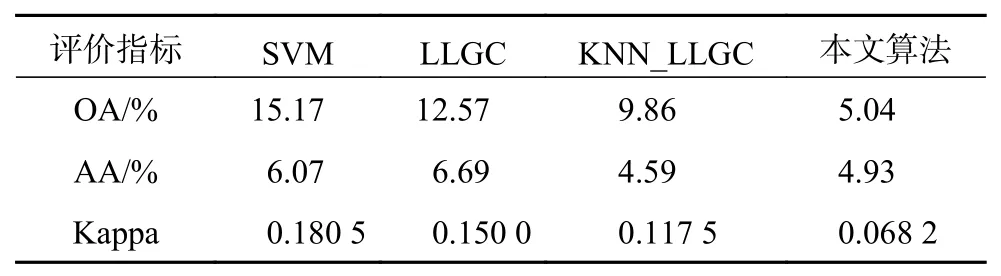
表4 Pavia高光谱数据集分类结果的波动幅度

图7、8给出了两数据集中4种方法的标记样本数和分类结果的关系曲线对比。横坐标为每类地物的初始已标记样本数量s，纵坐标为总体分类精度OA，已标记样本数取值：3、5、10、15、20、25。可以看出，在小样本条件下，本文提出的算法优于其他3种算法，在实际工作中高光谱图像往往面临有标签样本数较少的问题，本文算法可以在这种情况下表现更好。

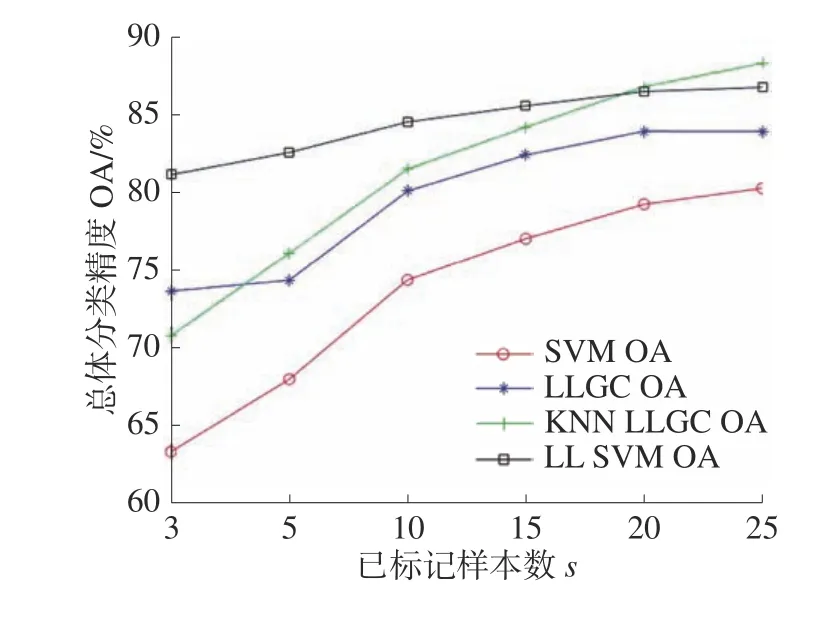
图7 Indian Pines数据集带标签样本数与OA的关系曲线

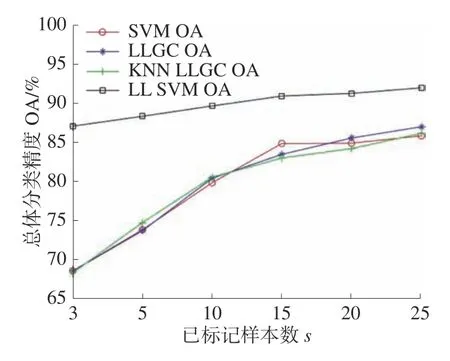
图8 Pavia数据集带标签样本数与OA的关系曲线

5 结论

针对LLGC算法的缺陷，本文提出了一种结合了LLGC和SVM的半监督分类算法，首先使用有标签样本训练SVM分类器对无标签样本进行预测，然后使用全部样本构造类别标记矩阵，通过LLGC算法对无标签样本进行预测，选取二者中预测结果相同的样本加入训练样本后重复上述步骤，直到到达预先设定的迭代次数。在Indian Pines和Pavia工程学院2组数据集上的实验证明了该算法能够克服传统LLGC算法和SVM算法的部分缺点，有效提高了分类精度及其稳定度。