Lemniscate of Leaf Function
Kazunori Shinohara
Department of Mechanical Systems Engineering,Daido University,10-3 Takiharu-cho,Minami-ku,Nagoya,457-8530,Japan
ABSTRACT A lemniscate is a curve defined by two foci,F1 and F2.If the distance between the focal points of F1-F2 is 2a(a:constant),then any point P on the lemniscate curve satisfy the equation PF1·PF2=a2.Jacob Bernoulli first described the lemniscate in 1694.The Fagnano discovered the double angle formula of the lemniscate(1718).The Euler extended the Fagnano’s formula to a more general addition theorem (1751).The lemniscate function was subsequently proposed by Gauss around the year 1800.These insights were summarized by Jacobi as the theory of elliptic functions.A leaf function is an extended lemniscate function.Some formulas of leaf functions have been presented in previous papers;these included the addition theorem of this function and its application to nonlinear equations.In this paper,the geometrical properties of leaf functions at n=2 and the geometric relation between the angle θ and lemniscate arc length l are presented using the lemniscate curve.The relationship between the leaf functions sleaf2 (l)and cleaf2 (l)is derived using the geometrical properties of the lemniscate, similarity of triangles,and the Pythagorean theorem.In the literature,the relation equation for sleaf2 (l)and cleaf2 (l)(or the lemniscate functions,sl(l)and cl(l))has been derived analytically;however,it is not derived geometrically.
KEYWORDS Geometry; lemniscate of Bernoulli; leaf functions; lemniscate functions; Pythagorean theorem; triangle similarity
1 Introduction
1.1 Motivation
An ordinary differential equation (ODE) comprises a function raised to the 2n-1 power and the second derivative of this function.Further, the initial conditions of the ODE are defined.

Another ODE and its initial conditions are given below:

The ODE comprises a functionof one independent variableand the derivatives of this function.The variablenrepresents a natural number (n=1,2,3,...).The above equation and the initial conditions constitute a very simple ODE.However, when this differential equation is numerically analyzed, mysterious waves are generated for all natural numbers.These mysterious waves are regular waves with some periodicity and amplitude.If these waves can be explained, they have the potential to solve various problems of nonlinear ODEs.
1.2 Theory of Leaf Functions
No elementary functions satisfy Eqs.(1)-(3).Therefore, in this paper, the function that satisfies Eqs.(1)-(3) is defined as cleafn(l).Functionr(l)is abbreviated asr.By multiplying the derivativedr/dlwith respect to Eq.(1), the following equation is obtained.

The following equation is obtained by integrating both sides of Eq.(7).

Using the initial conditions in Eqs.(2) and (3), the constantis determined.The following equation is obtained by solving the derivativedr/dlin Eq.(8).

We can create a graph with the horizontal axis as the variableland the vertical axis as the functionr.Because functionris a wave with a period, the gradientdr/dlhas positive and negative values, and it depends on domainl.In the domain,(See Appendix A for the constantπn), the above gradientdr/dlbecomes negative.

The following equation is obtained by integrating the above equation from 1 tor.
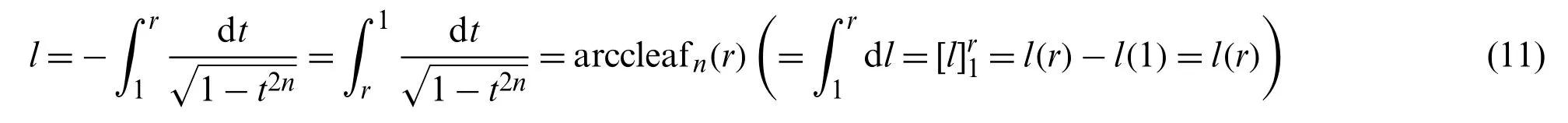
For integrating the left side of the above equation, the initial condition (Eq.(2),(l,r)=(0,1))is applied.The above equation represents the inverse function of the leaf function:cleafn(t)[1].Therefore, the above equation is described as

Similarly, the function that satisfies Eqs.(4)-(6) is defined asIn the domain,(See Appendix A for constantπn), the gradientbecomes positive.

The following equation is obtained by integrating the above equation from 0 tor.
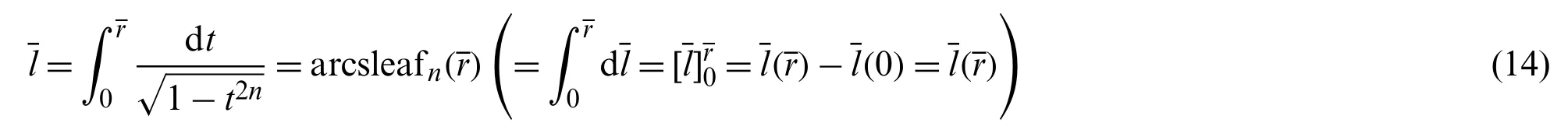
For integrating the left side of the above equation, the initial condition (Eq.(5),(l,r)=(0,0))is applied.The above equation represents the inverse function of the leaf function:[2].Therefore, the above equation is described as

1.3 Literature Comparison
Inverse leaf functions based on the basisn=1 represent inverse trigonometric functions.

In 1796, Carl Friedrich Gauss presented the lemniscate function [3].The inverse leaf functions based on the basisn=2 represents inverse functions of the sin and cos lemniscates [4].

In 1827, Jacobi [5] presented the Jacobi elliptic functions.Compared to Eq.(18), the termt2is added to the root of the integrand denominator.

Eq.(20) represents the inverse Jacobi elliptic function sn, wherekis a constant; there are 12 Jacobi elliptic functions, including cn and dn, etc.In Eq.(20), variabletis raised to the fourth power in the denominator.Jacobi did not discuss variabletraised to higher powers as indicated below.

Thus, historically, the inverse functions have not been discussed in the case of n = 3 or higher [6-14].
1.4 Originality and Purpose
A lemniscate is a curve defined by two fociF1andF2.If the distance between the focal points ofF1-F2is 2a (a:constant), then any pointPon the lemniscate curve satisfies the equationPF1·PF2=a2.Jacob Bernoulli first described the lemniscate in 1694 [15,16].Based on the lemniscate curve, its arc length can be bisected and trisected using a classical ruler and compass [17].Based on this lemniscate, a lemniscate function was proposed by Gauss around the year 1800 [3,18].Nishimura proposed a relationship between the product formula for the lemniscate function and Carson’s algorithm; it is known as the variant of the arithmetic-geometric mean of Gauss [19,20].The Wilker and Huygens-type inequalities have been obtained for Gauss lemniscate functions [21].Deng et al.[22] established some Shafer-Fink type inequalities for the Gauss lemniscate function.The geometrical characteristics of the lemniscate have been described[23,24].Mendiratta et al.[25] investigated the geometric properties of functions.Levin [26] developed analogs of sine and cosine for the curve to prove the formula.Langer et al.[27] presented the lemniscate octahedral groups of projective symmetries.As a kinematic control problem, a five body choreography on an algebraic lemniscate was shown as the potential problem for two values of elliptic moduli [28].The trajectory generation algorithm was applied by using the shape of the Bernoulli lemmiscate [29].
Leaf functions are extended lemniscate functions.Various formulas for leaf functions such as the addition theorem of the leaf functions and its application to nonlinear equations have been presented [30-32].
In this paper, the geometrical properties of leaf functions forn= 2, and the geometric relationship between the angleθand lemniscate arc lengthlare presented using the lemniscate curve.The relations between leaf functions sleaf2(l)and cleaf2(l)are derived using the geometrical properties of the lemniscate curve, similarity of triangles, and the Pythagorean theorem.In the literature, the relationship equation of sleaf2(l)and cleaf2(l)is analytically derived; however,it is yet to be derived geometrically [33].The relation between sleaf2(l)and cleaf2(l)can be expressed as
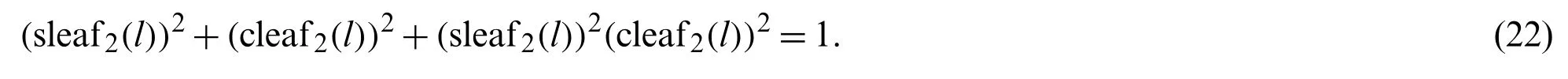
The Eq.(22) was analytically derived.However, it cannot be geometrically derived using the lemniscate curve because it is not possible to show the geometric relationship of the lemniscate functionssl(l)andcl(l)on a single lemniscate curve.In contrast, phaselof the lemniscate function and angleθcan be visualized geometrically on a single lemniscate curve.Therefore, in the literature, Eq.(22) is derived using an analytical method without requiring the geometric relationship.
In this paper, the angleθ, phasel, and leaf functions sleaf2(l)and cleaf2(l)(or lemniscate functionssl(l)andcl(l)) are visualized geometrically on a single lemniscate curve.Eq.(22) is derived based on the geometrical interpretation, similarity of triangles, and Pythagorean theorem.
2 Geometric Relationship with the Leaf Function cleaf2(l)
Fig.1 shows the geometric relationship between the lemniscate curve and cleaf2(l).Theyandxaxes represent the vertical and horizontal axes, respectively.The equation of the curve is

If P is an arbitrary point on the lemniscate curve, then the following geometric relation exists.

When point P is circled along the contour of one leaf, the contour length corresponds to the half cycleπ2(See Appendix A for the definition of the constantπ2).As shown in Fig.1, with respect to an arbitrary phasel, angleθmust satisfy the following inequality.

Here,kis an integer.
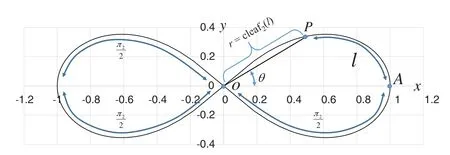
Figure 1:Geometric relationship between angle θ and phase l of the leaf function cleafn(l)
3 Geometric Relationship between the Trigonometric Function and Leaf Function cleaf2(l)
Fig.2 shows the foci F and F′of the lemniscate curve.The length of a straight line connecting an arbitrary point P and one focal point F is denoted by PF.Similarly, PF′denotes the length of the line connecting an arbitrary point P and a second focal point F′.On the curve, the product of PF and PF′is constant.The relationship equation is described as [34]

The coordinates of point P are
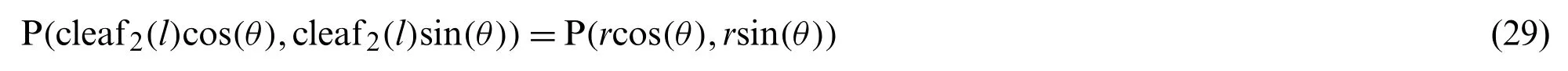
PF and PF′are given by

and
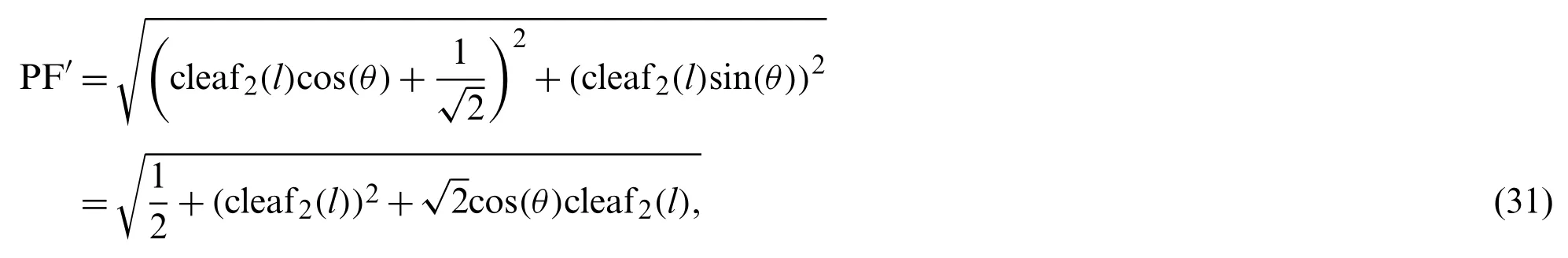
respectively.

Figure 2:Lemniscate focus
By substituting Eqs.(30) and (31) into Eq.(28), the relationship equation between the leaf function cleaf2(l)and trigonometric function cos(θ)can be derived as
After differentiating Eq.(32) with respect tol,

The following equation is obtained by combining Eqs.(32) and (33).
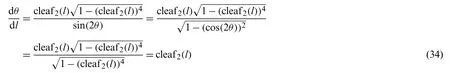
The differential equation can be integrated using variablel.Parametertin the integrand is introduced to distinguish it froml.The integration of Eq.(34) in the region 0 ≦t≦lyields the following equation (See Appendix C for details).

Therefore, the following equation holds.

Eq.(32) can only be described by variablelas


Eq.(38) satisfies the inequality of Eq.(27) under the conditionk=0.
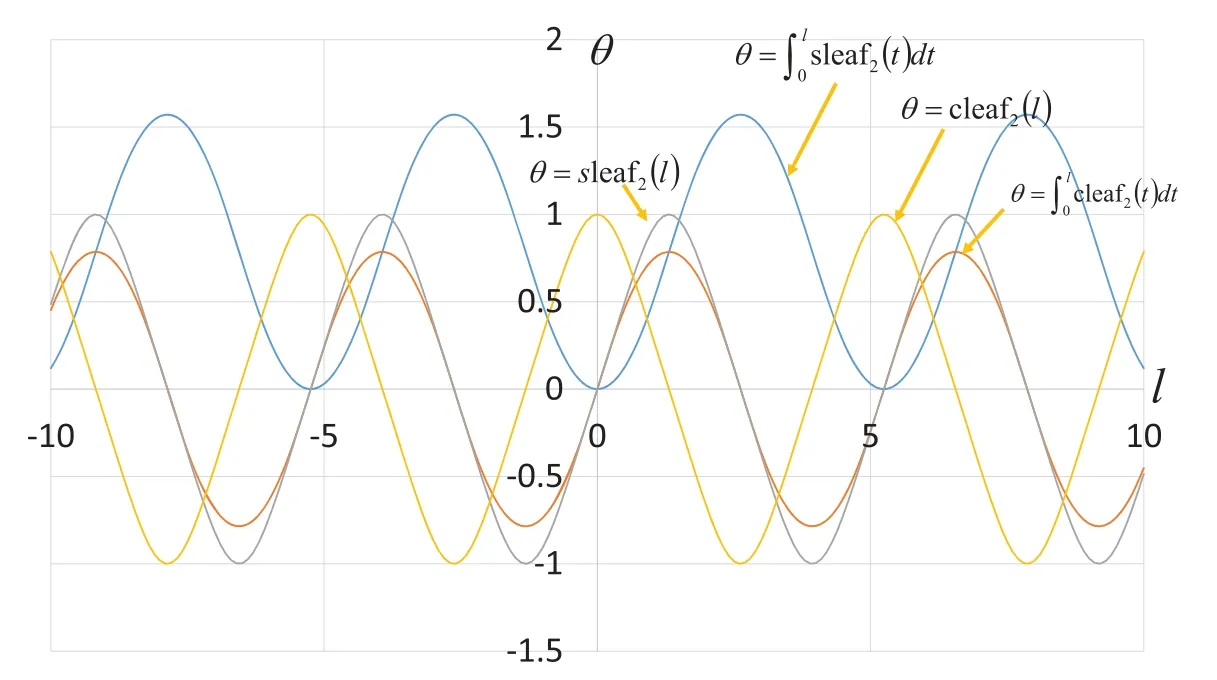
ure 3:Curves of leaf functions (sleaf2(l) and cleaf2(l)) and the integrated leaf functions(sleaf2(t)dt and cleaf2(t)dt)
Fig.4 shows the geometric relationship between functions sleaf2(l)and cleaf2(l).The geometric relation in Eq.(36) is illustrated in Fig.4.
Draw a perpendicular line from the point P on the lemniscate to the x-axis.This perpendicular is parallel to the y-axis.Let C be the intersection of this perpendicular and the x-axis.Therefore,the angle ∠OCP is 90°.Next, draw a line perpendicular to the x-axis from the intersection A(1,0)of the lemniscate and the x-axis.Let B be the intersection of this perpendicular and the extension of the straight line OP.Here,x=OC andy=CP.Substituting these into Eq.(23) gives

and

P and B are moving points, and point A is fixed.When angleθis zero, both P and B are at A.The geometric relationship is then expressed as cleaf2(l)=1=OA and sleaf2(l)=0=AB.Asθincreases, P moves away from A, and it moves along the lemniscate curve.Here, phaselof cleaf2(l)and sleaf2(l)corresponds to the length of the arcThe length of the straight line OP is equal to the value of cleaf2(l).Point B is the intersection point of the straight lines OP andx=1.In other words, P is the intersection point of the straight line OB and lemniscate curve.Asθincreases, B moves away from A and onto the straight linex=1.That is, it moves in the direction perpendicular to thexaxis.The length of straight line AB is equal to the value of sleaf2(l).Whenθreaches 45°, P moves to origin O and AB=1.The length of arc(or phasel) isπ2/2.Moreover, cleaf2(l)=0=OP and sleaf2(l)=1=AB.
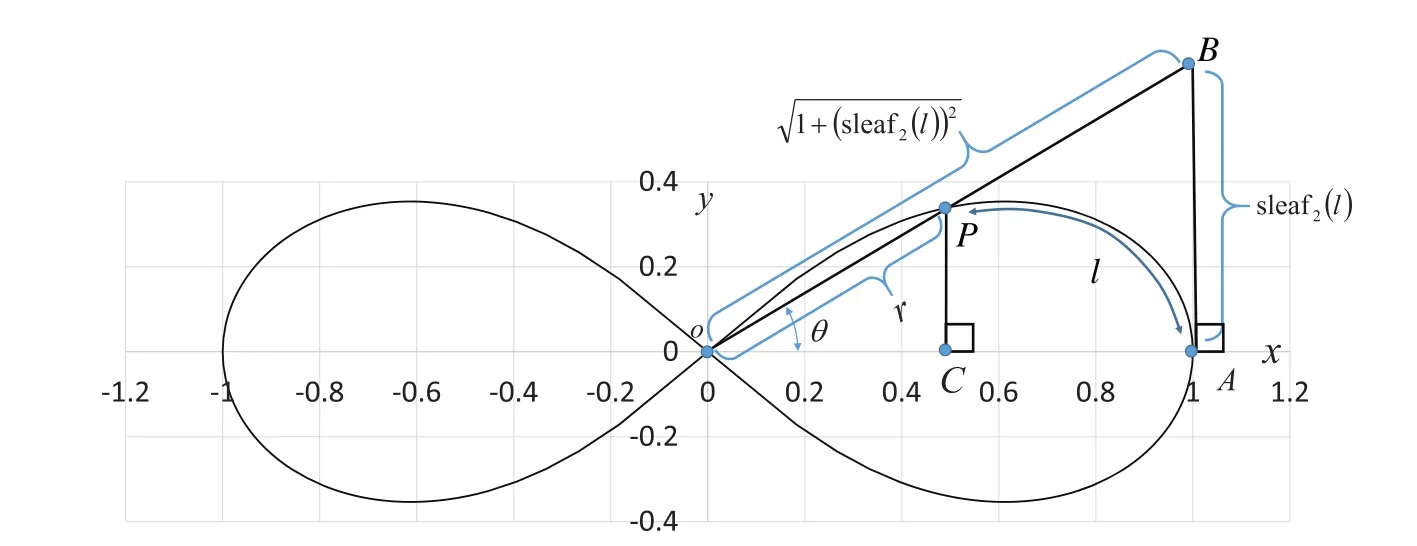
Figure 4:Geometric relationship between leaf functions sleaf2(l) and cleaf2(l)
The relationship OC:OA=CP:AB is derived by the similarity of triangles △OAB ~△OCP,as shown in Fig.4.Thus, the following equation holds.
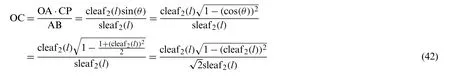
Eq.(32) is applied in the transformation process.Similarly, the relationship OP:PC=OB:BA is derived by the similarity of triangles △OAB ~△OCP, as shown in Fig.4.Therefore, the following equation holds.

By substituting Eqs.(42) and (43) into Eq.(39), the following equation is obtained.
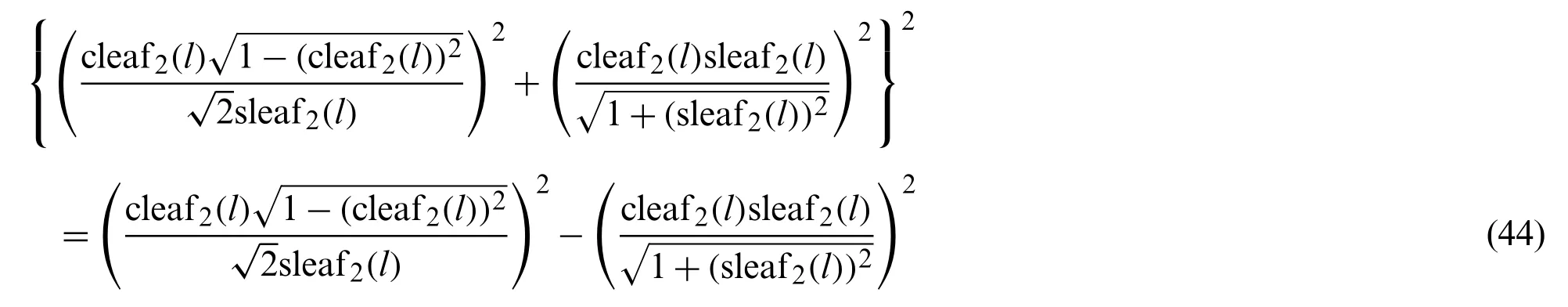
By rearranging Eq.(44), the following equation is obtained.
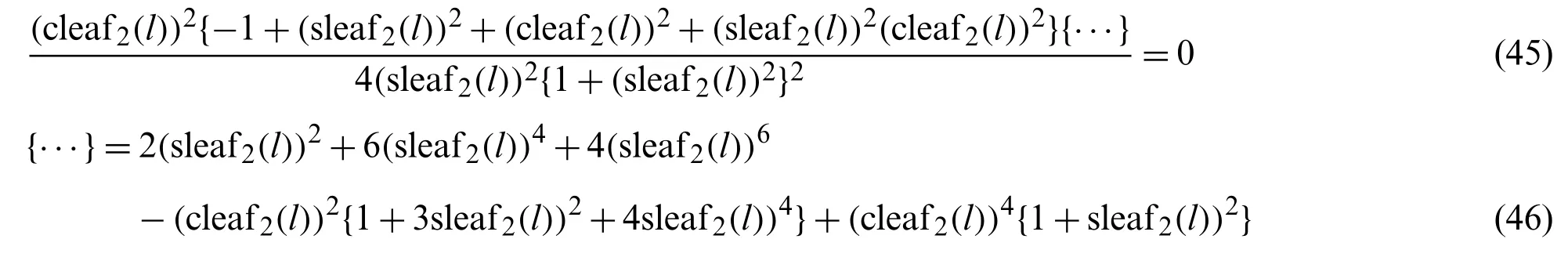
For arbitraryl, cleaf2(l)/=0 and {···}/=0.The relationship between sleaf2(l)and cleaf2(l)can then be obtained as Eq.(22).
4 Geometric Relationship of the Leaf Function sleaf2()
Fig.5 shows the geometric relationship between length sleaf2(l)and lemniscate curve inclined at 45°.In Fig.5, theyandxaxes represent the vertical and horizontal axes, respectively.The equation of this curve is given as


In Fig.5, for an arbitrary variable, the range of angleis given by

Here,kis an integer.

Figure 5:Geometric relationship between angle and phase of leaf function sleaf2()
5 Geometric Relationship between Trigonometric Function and Leaf Function sleaf2(l)

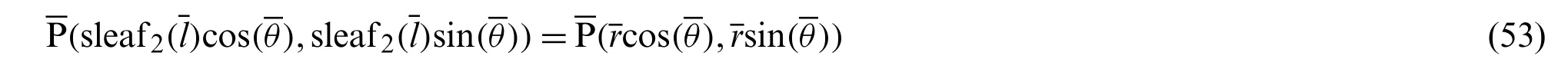
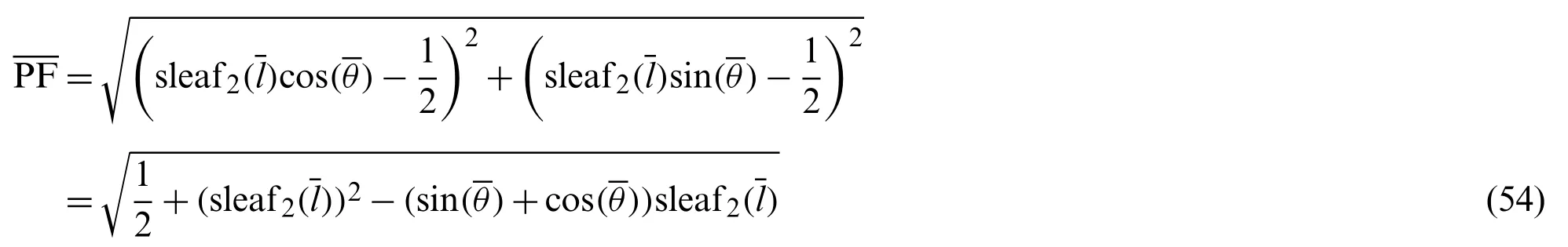
and
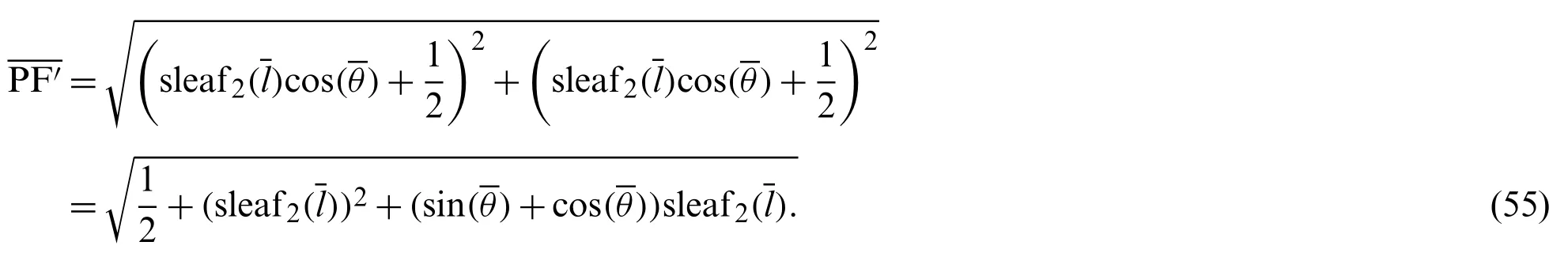
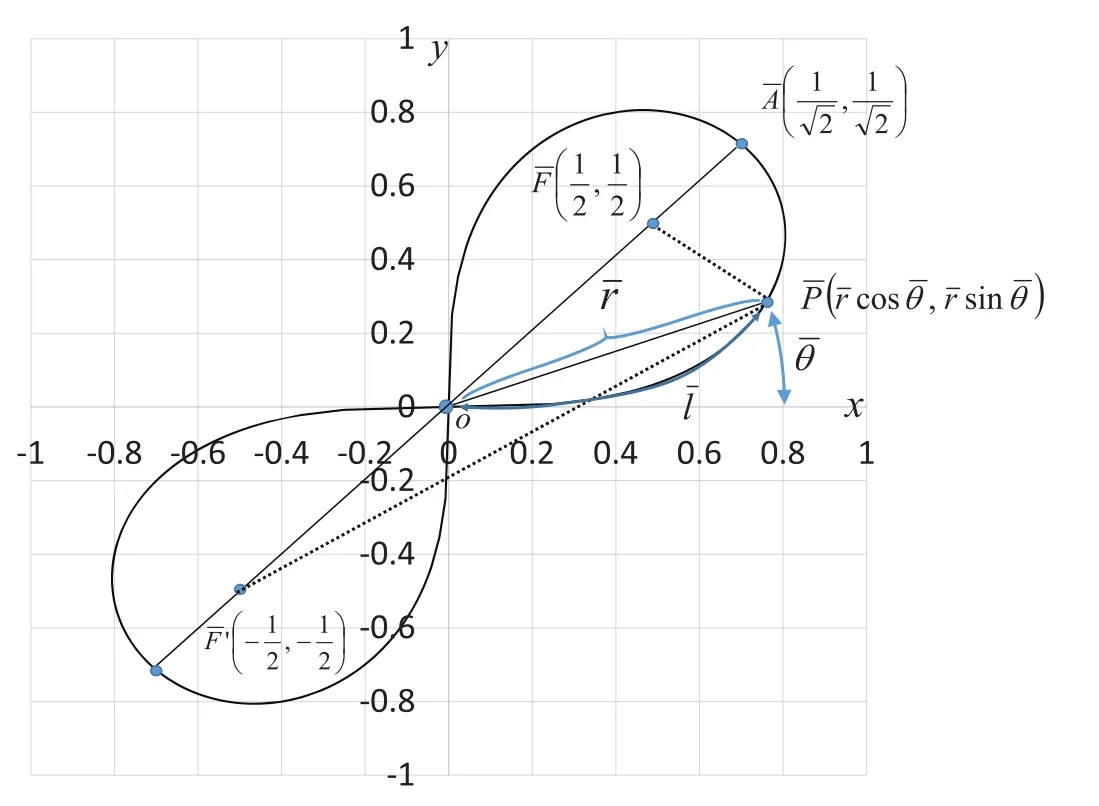
Figure 6:Lemniscate curve inclined at 45°
By substituting Eqs.(54) and (55) into Eq.(52), the relationship equation between the leaf function sleaf2() and the trigonometric function sin() can be derived as

The following equation is obtained by differentiating Eq.(56) with respect to the variabl e.

After applying Eq.(56), the equation is transformed as
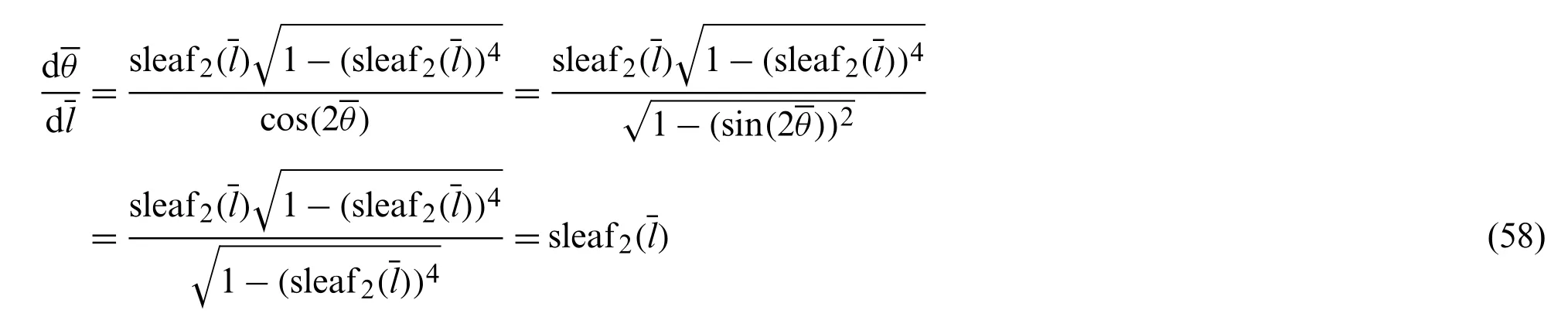
The differential equation is integrated by variable.Parameter t is introduced to distinguish the parameter from variablein the integration region.The integration of Eq.(58) in region 0 ≦t ≦(See Appendix C) yields

and the following equation holds.

Using Eq.(59), Eq.(56) can be described by variableas
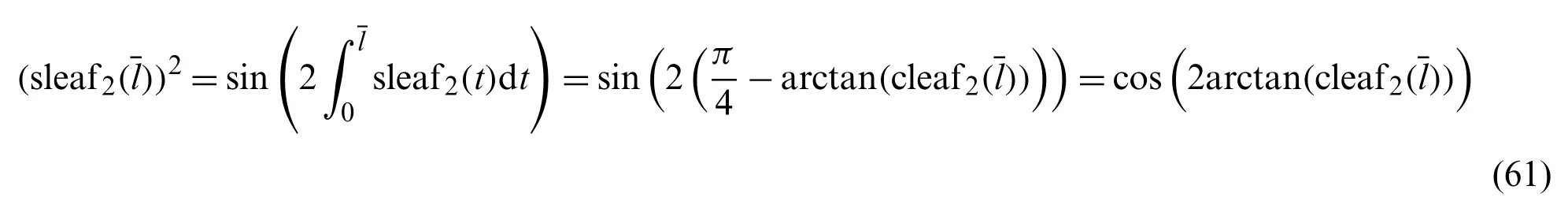

Eq.(62) satisfies the range of Eq.(51) under the conditionk=0.Fig.7 shows the lemniscate curve inclined at 45°.The geometric relation of Eq.(60) is added to Fig.7.


By substituting Eq.(65) into Eq.(47) and solving for variablex, four solutions can be obtained as


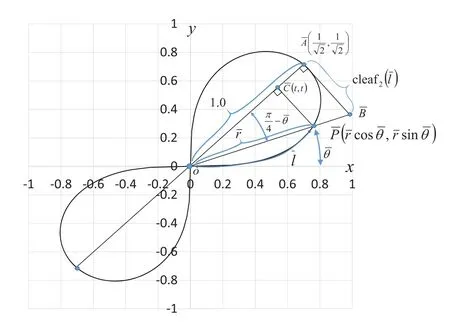
Figure 7:Geometric relationship based on the lemniscate curve inclined at 45°
As Eqs.(66) and (67) include imaginary numbers, the solutions forxusing both Eqs.(68)and (69) are determined by the intersection points of lineand the lemniscate curve, as shown in Fig.7.The largerxvalue is given by Eq.(69).That is, the coordinates of pointcan be expressed as
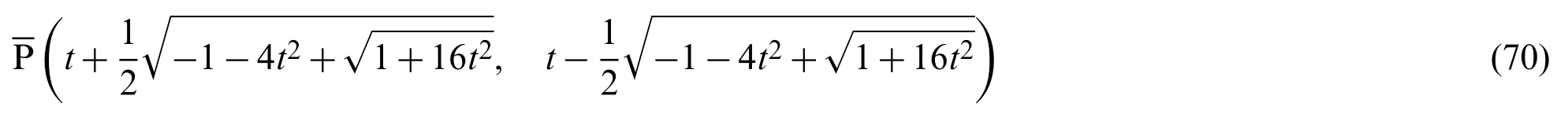

The following equation is obtained from the Pythagorean theorem of the triangle

Substitution of Eqs.(48) and (71) into Eq.(72) yields

The elimination of variabletfrom Eqs.(73) and (74) yields the relation equation, Eq.(22).
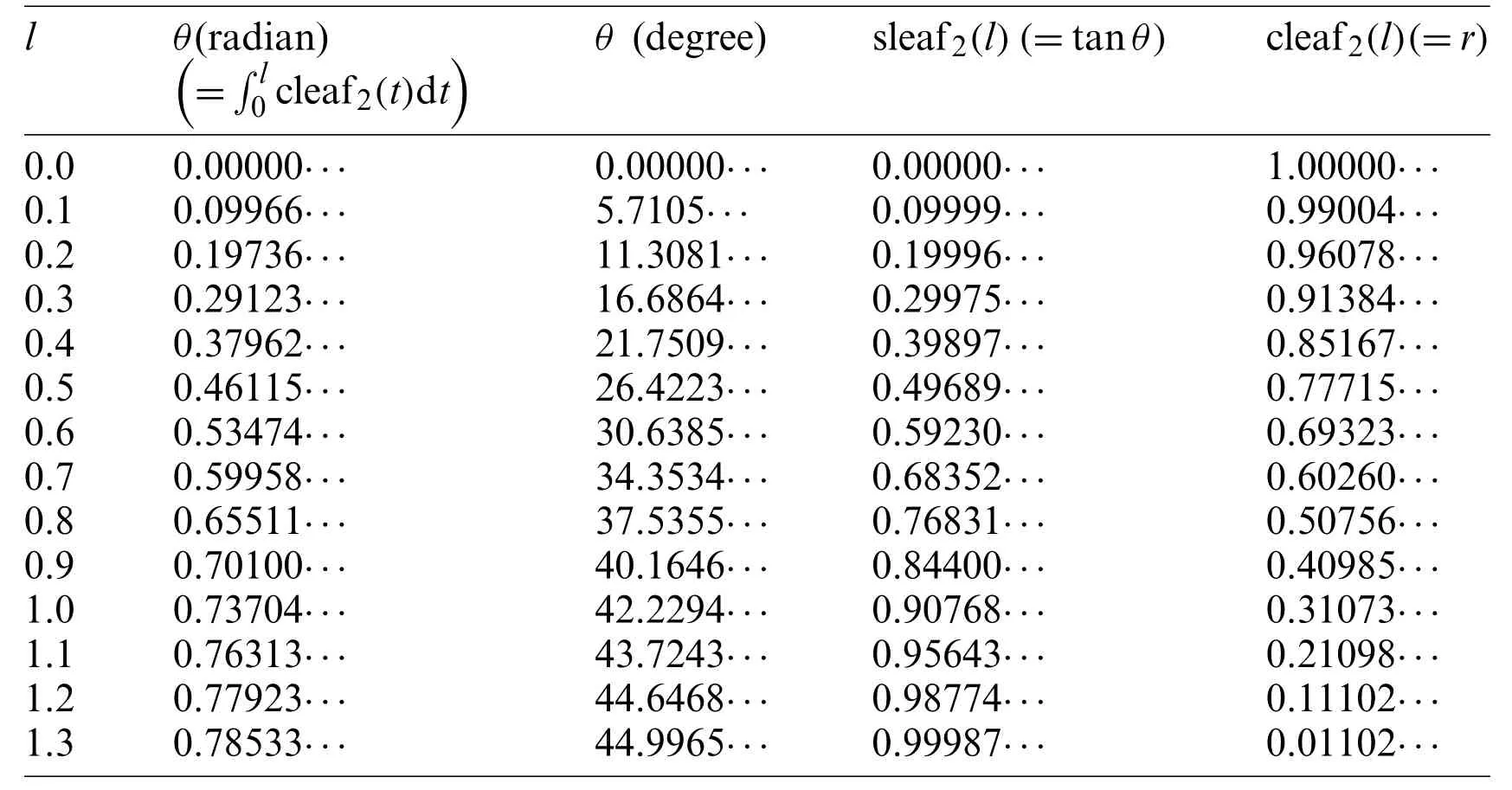
Table 1:Numerical data of arc length l, angle θ, and leaf functions sleaf2(l) and cleaf2(l)for Fig.4
Table 2:Numerical data of arc length angle and leaf functions sleaf2() and cleaf2()for Fig.7
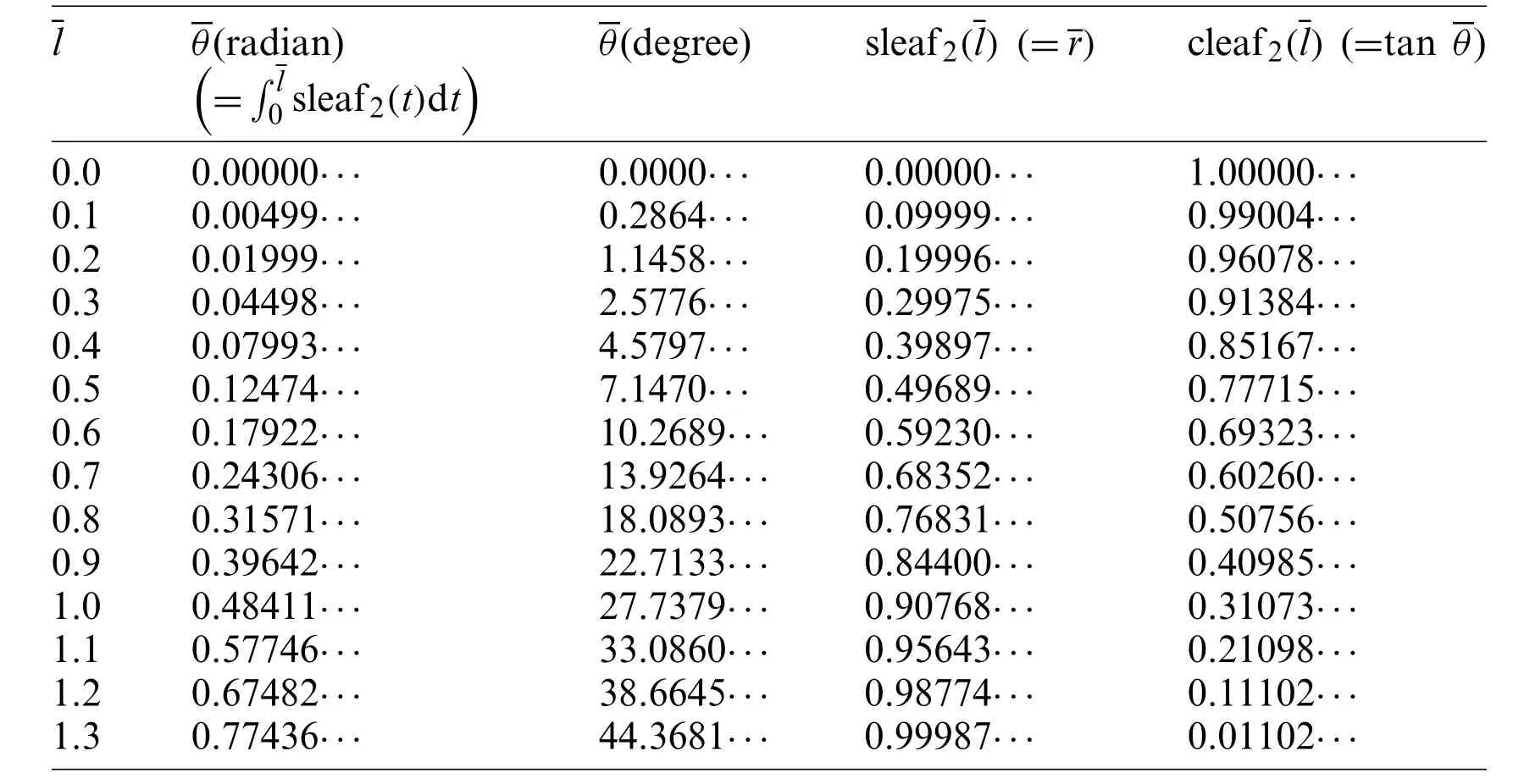
Table 2:Numerical data of arc length angle and leaf functions sleaf2() and cleaf2()for Fig.7
l θ(radian)images/BZ_283_593_1713_618_1759.png=∫l 0 sleaf2(t)dtimages/BZ_283_911_1713_936_1759.pngθ(degree) sleaf2(l) (=r) cleaf2(l) (=tanθ)0.0 0.00000··· 0.0000··· 0.00000··· 1.00000···0.1 0.00499··· 0.2864··· 0.09999··· 0.99004···0.2 0.01999··· 1.1458··· 0.19996··· 0.96078···0.3 0.04498··· 2.5776··· 0.29975··· 0.91384···0.4 0.07993··· 4.5797··· 0.39897··· 0.85167···0.5 0.12474··· 7.1470··· 0.49689··· 0.77715···0.6 0.17922··· 10.2689··· 0.59230··· 0.69323···0.7 0.24306··· 13.9264··· 0.68352··· 0.60260···0.8 0.31571··· 18.0893··· 0.76831··· 0.50756···0.9 0.39642··· 22.7133··· 0.84400··· 0.40985···1.0 0.48411··· 27.7379··· 0.90768··· 0.31073···1.1 0.57746··· 33.0860··· 0.95643··· 0.21098···1.2 0.67482··· 38.6645··· 0.98774··· 0.11102···1.3 0.77436··· 44.3681··· 0.99987··· 0.01102···
6 Numerical Results
Tab.1 lists the numerical values for Fig.4.The angleθand values of the leaf function(sleaf2(l)and cleaf2(l)) are calculated along the arc lengthl.The values of leaf functions cleaf2(l)are calculated by Eqs.(1)-(3).The values of leaf functions sleaf2(l)are calculated by Eqs.(4)-(6).Based on these data, the numerical data of functions sleaf2(l)and cleaf2(l)can be confirmed using Eq.(22).The function cleaf2(l)(=r)can also be confirmed by using Eq.(82).Angleθcan be calculated by using Eq.(35).
Tab.2 shows the numerical values for Fig.7.The angleand the values of leaf function(sleaf2and cleaf2) are calculated along the arc length.Based on these data, the function sleaf2=can also be confirmed using Eq.(90).The anglecan be calculated using Eq.(59).
7 Conclusion
Based on the geometric properties of the lemniscate curve, the geometric relationship among angleθ, lemniscate lengthl, and leaf functions sleaf2(l)and cleaf2(l)were shown on the lemniscate curve.Using the similarity of triangles and the Pythagorean theorem, the relationship equation of leaf functions sleaf2(l)and cleaf2(l)was derived.
Acknowledgement:The author gratefully acknowledges the helpful comments and suggestions of the reviewers that have improved the presentation of this paper.
Funding Statement:This research is supported by Daido University research Grants (2020).
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
Appendix A
The symbolsπnare a constant given by

The numerical data of the symbolπnare summarized in the Tab.3.

Table 3:Values of constants πn
Appendix B
The Eq.(23) of Cartesian coordinate system is transformed to the following equation of polar coordinates [1,3].

The variablerandθrepresents OP and ∠AOP in Fig.1.The arc length in the cartesian and polar coordinates is given by

The arc lengthlof the lemniscate with polar coordinates is given by

By differentiating Eq.(76) with respect to variableθ,

Then, by applying Eq.(79),
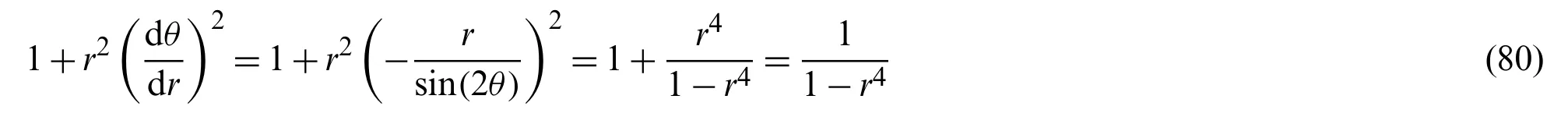
The following equation is applied to Eq.(80).

Hence, the arc lengthlbecomes

Appendix C
The following function is differentiated.
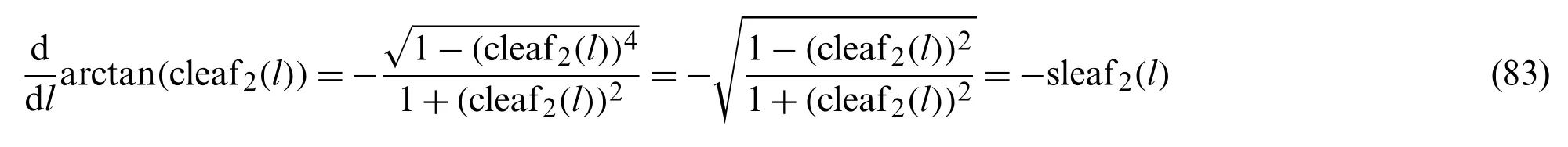
Integration of the above mentioned equation with respect tolyields

Similarly, the following function is differentiated with respect to variablel.
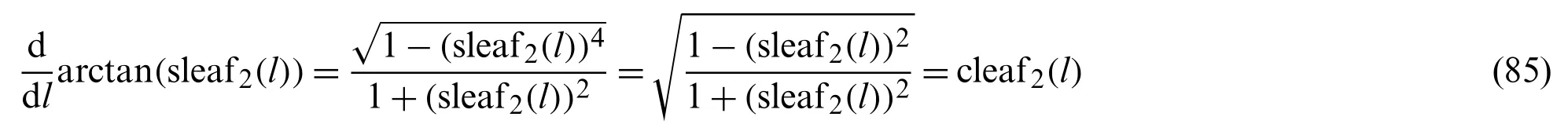
The following equation is obtained by integrating Eq.(85) with respect tol.
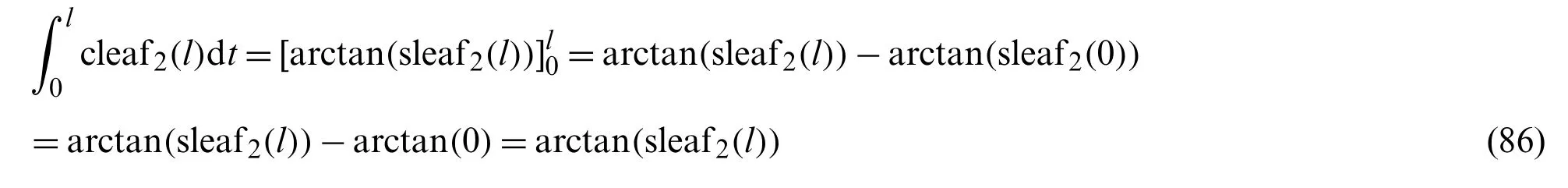
Appendix D
Eq.(47) of the Cartesian coordinate system is transformed to the following equation in the polar coordinates [2,35].

By differentiating Eq.(87) with respect to the variable,

Then, applying Eq.(88),
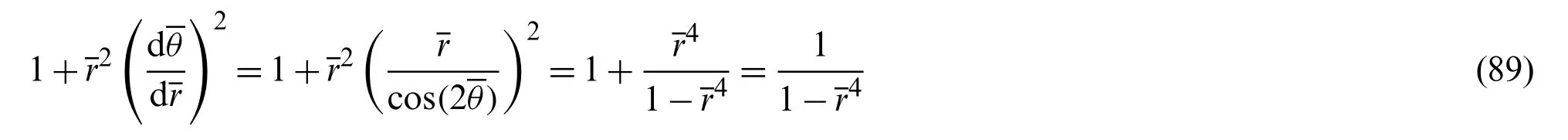
Hence, the arc lengthbecomes

 Computer Modeling In Engineering&Sciences2021年1期
Computer Modeling In Engineering&Sciences2021年1期
- Computer Modeling In Engineering&Sciences的其它文章
- Estimating the Impact of COVID-19 Pandemic on the Research Community in the Kingdom of Saudi Arabia
- Mesoscopic-Scale Numerical Investigation Including the Influence of Process Parameters on LPBF Multi-Layer Multi-Path Formation
- A Meshless Collocation Method with Barycentric Lagrange Interpolation for Solving the Helmholtz Equation
- Multiquadric Radial Basis Function Approximation Scheme for Solution of Total Variation Based Multiplicative Noise Removal Model
- Hybrid Security Assessment Methodology for Web Applications
- Isogeometric Boundary Element Analysis for 2D Transient Heat Conduction Problem with Radial Integration Method
