长输管道顺序输送混油高效数值模拟方法研究

王军防 陈雪娇 沈允 陈宇杰

1中国石化管道储运有限公司科技研发中心

2北京航天试验技术研究所

3中国石油北京油气调控中心

4中国石油大学（北京）

随着社会发展，我国对石油资源的需求量不断增加，尤其是沿海发达地区，但我国的石化资源主要分布在西部和东北地区，资源产地与经济发达地区存在空间的差异。因此，管道输送成为油品输送的主要方式，其具有效率高、运输能力大、连续性高、费用低等优越性[1]。但在成品油顺序输送的过程中，受到油品输送顺序、流速、地形、管道尺寸等多种因素的影响，使得相邻油品之间相互掺混，产生大量混油，造成极大经济损失。混油规律复杂，目前的技术很难对混油实现精确切割，而精确切割的关键是对混油段的跟踪[2]。

目前，混油研究方法主要包括实验[3-6]和数值模拟[7-9]。实验方法所需成本高，且采集数据困难，难以有效探究混油变化规律；数值模拟方法则成本低、操作简单，可运用于求解复杂流动问题。数值模拟方法广泛应用于成品油顺序输送管道混油浓度分布以及混油量的计算中，常用的混油数值模拟模型包括三维模型、二维模型和一维模型。三维模型计算精确，但计算量大，只适用于很短的管道[10]；一维模型简单，计算速度快，但计算精度较低，适用于雷诺数很大的情况[11]，是目前现场最常用的模型；二维模型可兼顾计算效率和精度，适用于较长管道的混油模拟[12]。以上三种模型的计算量均随着管道长度的增加不断增大，若采用常见的二维对流扩散方程求解一条100 km 的顺序输送管道混油量，所需的计算时间甚至长达一个月。低效的计算方法限制了混油数值模拟研究的发展，并且无法满足现场对混油量快速预测的需求。因此，亟待高效方法实现混油的快速求解，以满足长距离管道混油的研究与预测。

本文从控制方程求解方法和计算区域两个方面开展研究来实现高效的混油数值模拟。数值解法方面，常用的对流扩散方程求解方法包括直接求解和迭代求解。当求解区域很大时，直接解法的存储量和计算量均很大，而迭代解法的计算量和所需的存储空间均比直接法要少，更适合于长距离管道混油研究。常见的迭代求解方法包括雅克比迭代法、高斯-赛德尔迭代法、多重网格方法和预条件共轭梯度法，可通过选用高效的求解方法提高计算效率。计算区域方面，考虑到混油界面前方和后方均是纯油品，可跟踪混油区域，从减少计算区域角度入手提高计算效率。本文针对较精确的二维对流扩散模型，为满足混油高效、精确的数值模拟需求，进行以下方面研究：①对比一维和二维对流扩散模型求解结果和求解速度的差异；②基于二维模型，在不同管长条件下，对比高斯-赛德尔迭代法、多重网格方法和预条件共轭梯度法求解效率，选取用于混油数值模拟的高效求解方法；③基于高效求解方法，采用追踪方法跟踪混油段起始界面，探究混油段追踪方法在混油高效模拟中的适用性；④进行一维和二维模型的现场实例对比验证，探究二维模型能否实现快速、准确的混油数值模拟。

1 模型的建立

1.1 物理模型

直接对实际的三维管道进行混油模拟，计算量巨大。若忽略重力对混油的影响，则顺序输送管道混油的浓度分布可用一个过管道中心轴线的二维平面来表示，三维问题就可简化为平面二维问题进行处理（图1）。而二维平面上的成品油浓度上下对称分布，计算区域进一步简化为x轴上半部分，如果管道径向的流速和油品浓度分布均匀，则可近似化简成一维问题进行处理。

图1 管道简化示意图Fig.1 Schematic diagram of simplified pipeline

1.2 数学模型

1.2.1 一维模型

正常输送情况下，物性不同的两种油品之间的掺混过程主要包括对流扩散和分子扩散两部分。其中对流扩散主要是由湍流脉动引起的，而分子扩散是由径向浓度梯度引起的。当雷诺数足够大时，对流扩散远大于分子扩散，湍流脉动使得管道界面流速和混油浓度分布趋于均匀，此时引入有效扩散系数，借助费克扩散定律和质量守恒定律可得一维简化模型。

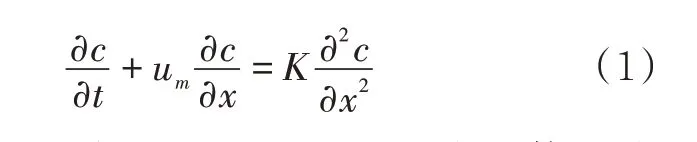
式中：c为前行油品截面处油品平均浓度（体积分数，下同）；um为油品的平均流速，m/s；K为有效扩散系数，可采用式（2）计算，m2/s；t为时间，s；x为轴向坐标位置，m。

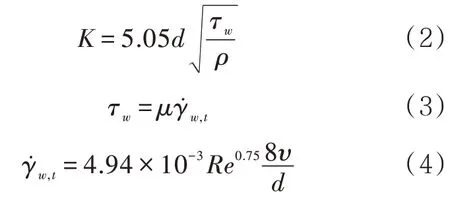
式中：ρ为油品密度，kg/m3；τw为壁面剪切应力[13]，N/m2；γ˙w,t为壁面剪应变，s-1；μ为油品的动力黏度，Pa·s；υ为油品的流速，m/s；Re为雷诺数；d为管道直径，m。

1.2.2 二维模型

成品油顺序输送的正常工况一般为圆管充分发展的恒定湍流，主要包括层流底层、缓冲层和湍流核心区。二维模型充分考虑径向不同流态区域流速和混油扩散系数的差异，针对不同的区域分别进行处理。在圆柱坐标下，针对图1 中2πr、dr、dx的微元体，同样借助费克扩散定律和质量守恒定律建立二维对流扩散方程[14]。

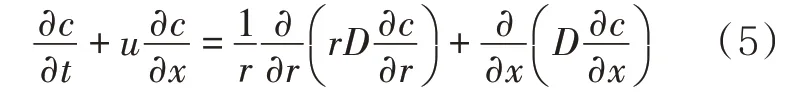
式中：u为管道截面流速分布，m/s；r为到管道中心的距离，m；c为前行油品浓度；D为扩散系数，m2/s。

不同流态区域的速度分布和扩散系数采用经验公式计算[12]。

1.2.3 边界条件和初始条件

管道中充满前行油品，从0 时刻开始，后行油品进入管道，二维混油数值模拟在管道壁面和中心处沿径向的浓度梯度为0，边界条件见式（6），一维混油数值模拟边界条件见式（7）。值得注意的是，对于二维模型，壁面处采用无滑移边界条件，无法有效考虑壁面对油品的黏附作用。因此，无法考虑油品输送顺序对混油带来的影响。

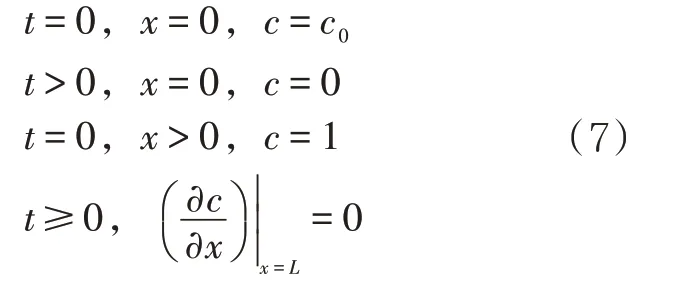
式中：c0为管道起点前行油品初始浓度；L为管道全长，m。

1.3 网格划分

一维模拟直接采用一维均分网格，二维模拟管壁处采用无滑移边界条件，在壁面的作用下，存在较长的混油尾迹，对混油的产生和发展具有重要的影响。为了精确捕捉近壁面区的信息，需要在近壁面区采用密集的网格，而研究表明，湍流核心区可以采用尺度较大的网格而计算精度并不会明显降低[15]。因此在壁面法向采用式（8）和（9）进行网格划分。

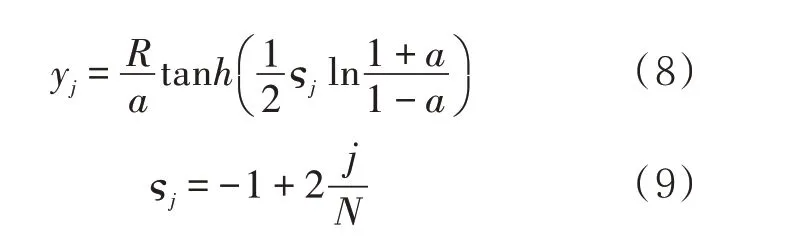
式中：yj为y方向第j个节点的位置；N为y方向总的节点个数；a为网格变化的调节参数；ςj为中间变量。

1.4 方程求解

求解混油浓度的控制方程式（1）属于对流占优的扩散方程，一般采用两步法[16]进行求解，见式（10）、式（11）。其基本思路是：将对流扩散方程分解成一个纯对流方程和一个纯扩散方程，在前半个时步采用特征线法求解纯对流方程，在后半时步采用隐式有限容积方法求解扩散方程，如此循环直到求解完成。值得注意的是，在进行纯对流方程求解时，需采用高阶格式，防止假扩散带来的数值误差[16]。

特征线法直接求解纯对流方程速度较快，而纯扩散方程则一般采用迭代法求解，速度较慢。目前，主要采用高斯赛德尔迭代法、多重网格方法和预条件共轭梯度法求解纯扩散方程。

2 模拟结果

为高效准确地进行混油数值研究，首先对比一维和二维模型的求解结果和求解效率，其次从高效求解方法和减少计算区域两个角度分别提升二维混油模型计算效率，最后将高效求解方法运用到二维模型中，进行现场实例验证分析，并和一维模型计算效率相对比。

2.1 网格无关解验证

在进行具体的混油数值模拟研究之前需确定一套合适的网格，为后续工作的开展提供支持。本文以规格为355 mm×6.4 mm、长度为1 km 的管道为例进行网格无关解验证。混油长度定义为前行油品浓度为1%～99%的管段长度。时间步长（一维模型中umax=um，本文所有时间步长都按照该方法计算），当相邻两套网格计算得到的混油长度之差小于3%时，即认为得到网格无关解。二维模型网格信息见表1，一维模型网格信息见表2，油品物性以呼包鄂管道为参考，具体参数见表3（本文所涉及的计算均采用该油品的物性参数）。

表1 二维模型网格无关解验证的网格信息Tab.1 Grid information for grid independent solution verification of 2D model

表2 一维模型网格无关解验证的网格信息Tab.2 Grid information for grid independent solution verification of 1D model

表3 呼包鄂管道油品物性Tab.3 Physical properties of oil products in Hu-Bao-E Pipeline

在表1 和表2 中的三种网格条件下，二维模型和一维模型在终点处混油分布如图2 所示。两种模型在三套网格下的计算结果近似，其中二维模型1 000×20 的网格和2 000×40 的网格所计算的混油长度为57.5 m 和57.75 m，相对差异为0.43%；一维模型1 000 个网格和2 000 个网格的计算的混油长度为58.06 m 和59.03 m，结果相差1.64%。所以可选择1 000×20 的网格作为二维模型的计算网格，1 000 的网格作为一维模型的计算网格，基于相应的网格比例开展具体混油数值模拟研究。

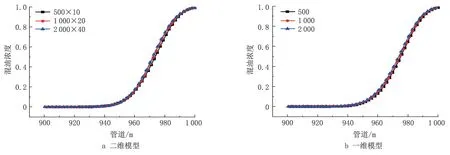
图2 一维和二维网格无关解验证Fig.2 Verification of 1D and 2D models gird independent solutions

2.2 一维模型和二维模型比较

目前常用的混油理论模型包括一维对流扩散模型和二维对流扩散模型。本文以3 km 管道为例，对比两种模型的计算结果和效率。一维模型和二维模型在终点处的浓度分布如图3 所示，3 km 处前行油品浓度均为99%，对应的混油长度为103 m 和101.5 m，相对差异为1.46%。所以两种模型从计算结果角度来看，差异不大。但从计算角度来看，一维模型的计算速度远快于二维模型。尽管如此，一维模型只能使用于高雷诺数，且一维模型无法描述混油浓度在管道中分布的情况，这无疑限制了一维模型的使用。而二维模型与一维模型相反，有很强的适用性，可描述混油浓度分布情况（图4），但计算效率低。如果能大幅度提高二维模型计算效率，则可为高效精确的混油数值模拟研究提供参考。

2.3 混油高效求解方法探究

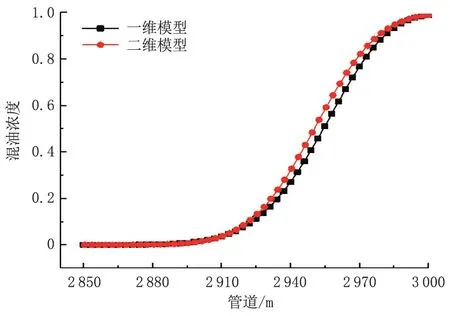
图3 一维和二维模型计算结果对比Fig.3 Comparison of calculation results of 1D and 2D models

图4 二维混油分布云图Fig.4 2D contamination distribution cloud chart

为了探究适合于二维混油纯扩散方程的高效求解方法，在保持网格尺寸不变的情况下，通过改变管道长度来对比高斯赛德尔迭代法、多重网格方法和预条件共轭梯度法在不同管段长度下的计算效率。计算效率的判定标准为求解时间，从0 时刻后行油品进入管道开始计时，当终点处前行油品的管道截面处油品平均浓度小于99%时结束计时（表4、图5）。

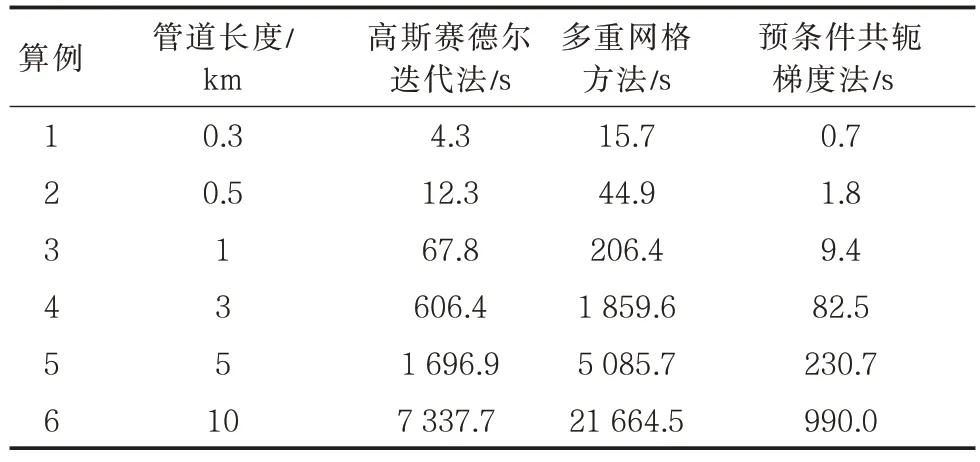
表4 不同求解方法计算结果Tab.4 Calculation results of different solution methods

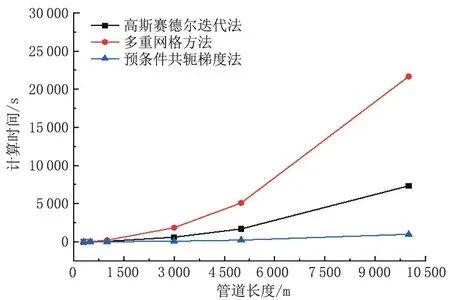
图5 不同求解方法计算耗时曲线Fig.5 Calculation time curve of different sloution methods

从表1 和图5 中可以看出，当管道长度相同时，与传统的高斯赛德尔迭代法相比，预条件共轭梯度法的求解速度更快，在求解过程中只需迭代一次便可得到收敛解。而多重网格方法反而变慢，其主要原因是扩散系数在不同的流态区域大小不同，且差异较大。在多重网格实施过程中，粗网格上的物性参数可能是从不同区域限定得到的，反而导致误差被放大，最终导致密网格上的收敛速度减缓。

从图5 中无法直观看出不同求解方法的加速效果随管道长度的变化，因此，以传统的高斯赛德尔迭代法为基准来计算多重网格方法和预条件共轭梯度法与其的加速比。如图6 所示，随着管道长度增加，预条件共轭梯度法相对高斯赛德尔迭代法的加速比从6.14 增加到7.41，加速效果越来越好。除此之外，多重网格方法的计算效率也在不断接近高斯赛德尔迭代法。

图6 不同求解方法计算耗时加速比Fig.6 Calculation time speed-up ratio of different solution methods

综上可以看出，预条件共轭梯度法求解混油纯扩散方程的效率最高，并且加速效果随着管道长度的增加而略有提高。

2.4 混油段跟踪方法

虽然预条件共轭梯度法的求解效率相对于传统的高斯赛德尔方法已有较大幅度提高，但仍无法满足长距离管道混油数值模拟研究。从图5 可以看出，当管道长度增加后，其计算时间显著增加，采用拟合方法对共轭梯度法计算时间与计算管道长度的关系进行拟合，得

式中：l为管道长度，m；t为计算时间，s。

按照该拟合式，预估300 km 的管道至少需要超过10 d 的模拟时间，而现场混油段只需不到3.5 d的时间便可到达终点，连现场都无法做到混油提前预测。因此，需要对混油模拟过程进行进一步加速。

混油只存在于不同油品的交界面上，而管道的绝大部分区域都是纯油品，在进行混油模拟过程中对纯油品区域的计算无任何意义。因此，基于预条件共轭梯度法，通过采用混油段跟踪方法减小计算区域大小，从而实现混油模拟过程的进一步加速，其基本操作过程如图7 所示。本文选取的混油段起始位置分别为前行油品浓度为10-10和1-10-10的位置。值得注意的是，在保存混油段起始位置的时候，需增加少量网格（本文选取10 个网格），以保证混油界面在求解过程中不会超出求解区域。

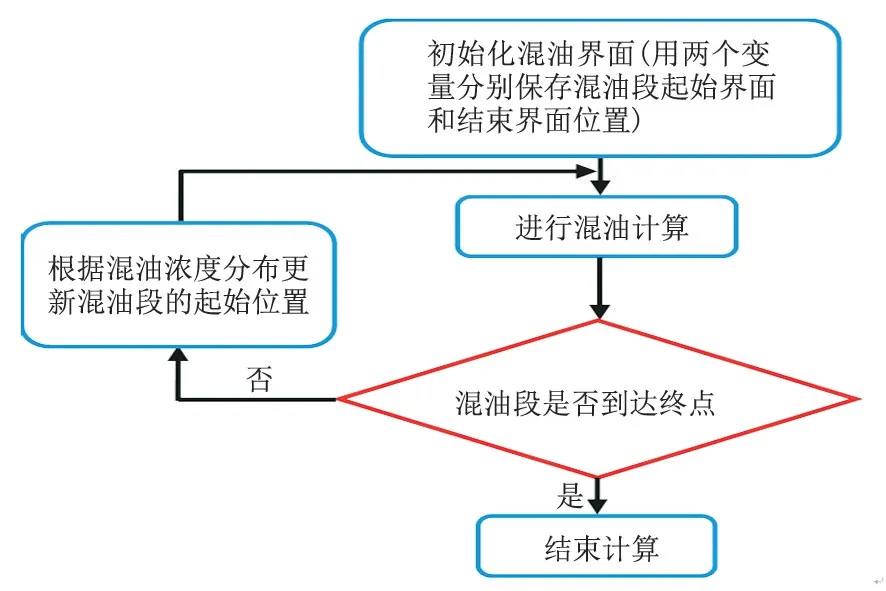
图7 混油段跟踪思路Fig.7 Tracking idea of contamination segment

在进行不同管道长度下计算效率的对比之前，需对混油段追踪方法计算结果的正确性进行验证，以确保该方法不会给计算结果增加误差。以355 mm×6.4 mm、长度为1 km 的管道，流速为1 m/s 工况为例计算，结果如图8 所示。从图8 可以看出，两条曲线完全重合，并且在浮点数类型自动保存的6 位小数的范围内误差为0。因此，混油段跟踪方法不会给模拟结果带来额外的误差。

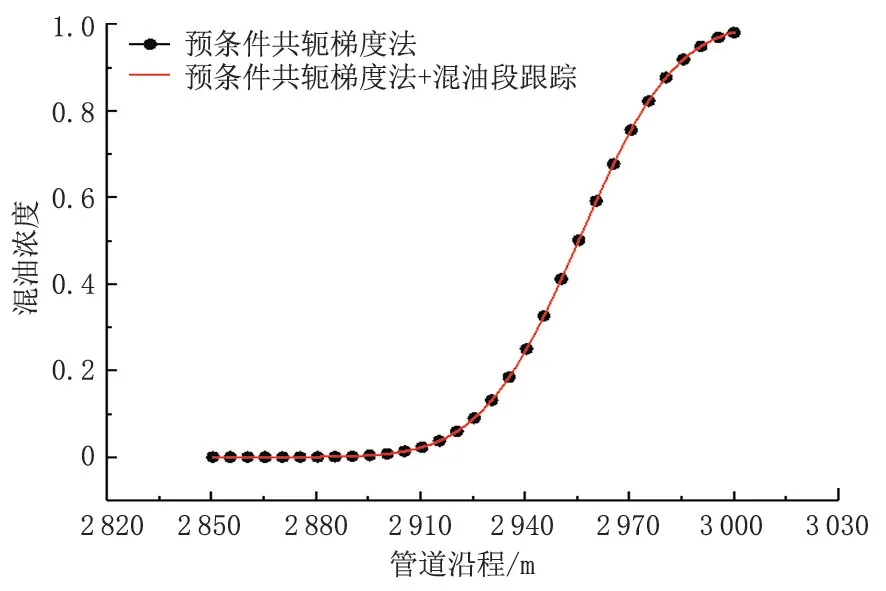
图8 混油段跟踪方法计算结果精度验证Fig.8 Accuracy verification of calculation results of contamination segment tracking method

由于常规方法求解效率较低，无法应用于较长管道，因此，采用表4 中对应的不同管道长度进行具体的混油段追踪方法应用分析。利用混油段跟踪方法计算前几组算例，所需的时间较短，比较意义不大，因此将对后几组数据进行重点比较。采用混油段跟踪方法计算的结果如表5，图9 所示。

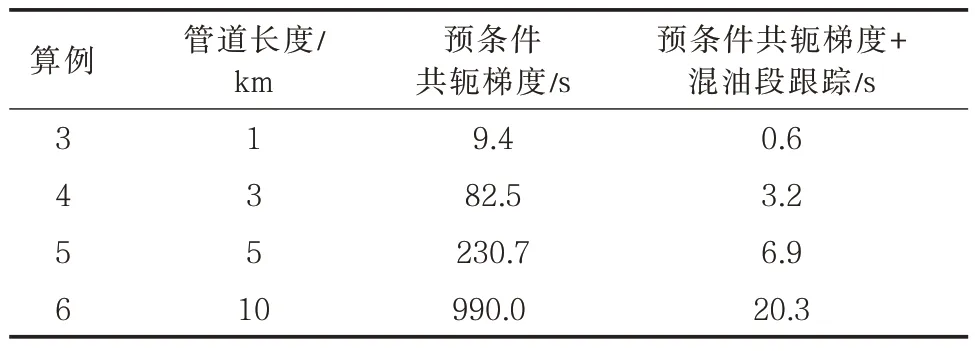
表5 混油段跟踪方法计算结果Tab.5 Calculation results of contamination segment tracking method

图9 混油段跟踪加速结果Fig.8 Acceleration results of contamination segment tracking method

从图9 中可以看出，混油段跟踪方法的运用实现了进一步加速，且随着管道长度的增加，加速比从15.67 增加到48.77，10 km 的管道可实现48.77 倍的加速，这是因为混油段跟踪方法极大缩小了计算区域，管道越长，混油段占管道全长的比例越小，使得加速效果随计算区域的变大而大幅度提高。

综上可以看出，混油段跟踪方法可显著提高混油模拟效率，并且只跟踪混油段，计算区域随管道全长变化很小，可适用于长距离管道的混油模拟计算。

2.5 现场实例运用

根据前文分析结果，采用呼包鄂成品油顺序输送管道实际混油验证程序的正确性和适用性。由于无法获取管道终点处密度变化的数据，因此直接采用管道处终点的混油量进行对比验证。油品物性参数、管道参数如表3、表6 所示，油品流速采用平均流速。

表6 呼包鄂管道参数Tab.6 Parameters of Hu-Bao-E Pipeline

根据已知现场参数进行数值模拟，计算结果如图10和表7所示。鄂尔多斯进站的混油量为90.32 m3，与现场数据95.00 m3之间的相对误差为4.93%。由于模拟过程中未考虑局部管件、重力、地形、流速变化等因素对混油量的影响，模拟结果应比实际过程偏小一些，因此本文模拟计算结果在合理范围内。另一方面，现场混油界面从起点到终点所需时间约为275 005.0 s，而模拟耗时为3 293.5 s，为现场所需时间的1.12%，可实现现场混油量的快速超前预测。

在相同的管长情况下，如果不采用混油段追踪方法，只采用预条件共轭梯度法求解一维模型，所需的计算时间为3 592.7 s，比二维模型采用最终方法计算所需时间还长，所以预条件共轭梯度法+混油段跟踪方法可实现快速、精确的混油数值模拟。

图10 呼包鄂管道混油模拟结果Fig.10 Simulation results of contaminated oil in Hu-Bao-E pipeline

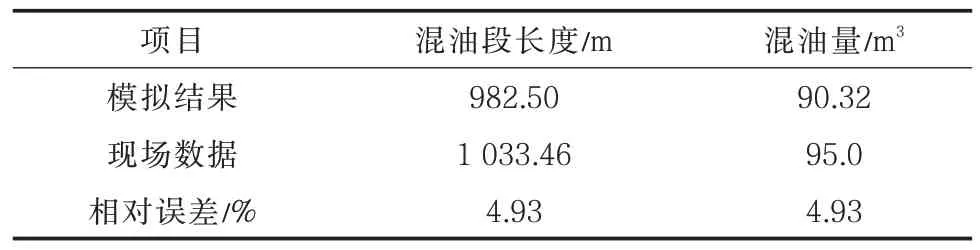
表7 模型验证结果Tab.7 Validation results of model

3 结论

从优选求解方法和减小计算区域两方面研究提高混油数值模拟的计算效率。对比得到预条件共轭梯度法可实现混油代数方程组的高效求解；通过实现混油段的跟踪模拟，进一步大幅度提高了混油数值模拟的计算效率。将本文研究成果成功运用于现场管道，得到具体结论如下：

（1）预条件共轭梯度法可实现混油纯扩散过程的高效计算。在不同管道长度下，预条件共轭梯度法的求解效率均高于传统的高斯赛德尔迭代法，针对0.3～5 km 的管道，实现了6.14～7.41 倍的加速，随着管道长度的增长（网格量变大），预条件共轭梯度法的优势更加明显。但多重网格方法由于扩散系数随空间变化，导致求解效率比传统方法更低。

（2）混油段跟踪方法在保证精度的前提下可实现混油数值模拟效率的显著提升。在求解过程中，纯油品区域不进行求解而只求解混油段，因此管道越长，混油段所占的比例越小，加速比越大，10 km的管道实现了48.77 倍的加速。更为重要的是，该方法不受管道长度的限制，计算量只依赖于混油段长度，可适用于长距离管道。

（3）研究成果可适用于现场对混油的提前预测。通过将研究成果运用于呼包鄂成品油顺序输送管道，所得混油结果的相对误差为4.93%，模拟耗时为现场混油界面从起点到终点所需时间的1.12%。因此，本文研究成果可为现场管道混油分布及混油量的高效模拟提供参考。