空间知识挖掘的自然面群聚集度聚类方法
刘呈熠,武 芳,巩现勇,行瑞星,杜佳威
信息工程大学地理空间信息学院,河南 郑州 450001
以湖泊、岛屿为代表的自然面群是地图的重要组成部分,其形状、尺寸、方向等几何特征存在较大差异,而且具有整体分散、局部聚集、聚集程度不一的分布特征。自然面群的空间分布特征是影响地图综合的重要因素[1-2],识别、挖掘空间聚集特征是研究的难点之一[3]。当前,面群的空间聚类方法已有不少成果[4],根据算法类型主要可分为:①划分聚类算法。通过不断优化目标函数来达到预设聚类要求,如k-means算法[5]、SOM算法[6]等。这类算法通过多次迭代得到最优的聚类结果,但易陷入局部最优问题,且受预设值制约。②层次聚类算法。在面群邻近关系的基础上,采用分割或聚合的策略获得聚类结果,如最小生成树法[7]、Delaunay三角网法[8-12]、图卷积神经网络算法[13]、MSSCP算法[14]、缓冲区法[15]等。这类算法多适用于相似度高、分布规则的面群聚类问题,但对于几何特征差异大、分布特征复杂的自然面群聚类不适用。③密度聚类算法。以密度为核心参数,不断聚合邻域范围内满足预设规则的对象来获得聚类结果,如DBSCAN算法[16]、似最小生成树法[17]、密度峰值算法[18-19]等。这类算法能够识别异形簇,但多用于点簇聚类。
分布密度作为描述地物聚集程度的一项重要指标,其背后往往隐含某种地理意义,如湖泊群密度反映区域降水量,岛屿群密度反映地质构造[20]等。根据Gestalt原理的邻近性和相似性原则[21-22],围绕自然面要素的邻近距离和分布密度,本文提出一种基于聚集度和边界最短距离的自然面群聚类方法(natural polygon features clustering,NPFC),并进行如下工作:①为克服分布密度定义不适用的问题,定义一种新的面要素分布密度度量参数——聚集度,分析不同条件下聚集度的变化特点,验证其有效性;②为解决离散面聚合问题,根据聚集度向量识别聚类中心,并提出一种基于聚类中心的群组生长模型;③为消除过度划分问题,设计边缘检测和群组合并策略,获得更优的聚类结果。
1 面要素聚集度
1.1 聚集度的定义
地物的分布密度通常指单位面积内地物对象的数量[23],数量越多,该地物的分布密度就越高。然而,面要素具有一定尺寸,计数区域难以统一划定;同时采用计数方式忽视了面要素的尺寸差异,无法正确反映地物的分布密度。面要素的分布密度受到尺寸、邻域大小和邻近面数量共同影响。面要素尺寸一般采用面积来描述,本文采用面积与对应Voronoi图面积的比值描述其聚集程度;考虑到面要素的一阶邻域是其最邻近、影响最直接的区域,将该区域作为计算分布密度的邻域范围,并根据文献[18]选用高斯核函数控制邻近距离对中心面要素分布密度的影响程度;邻近面数量为其一阶邻域范围内包含的所有面要素数量。据此本文提出面要素“聚集度”的概念,记为δ(i),其计算公式如下
(1)
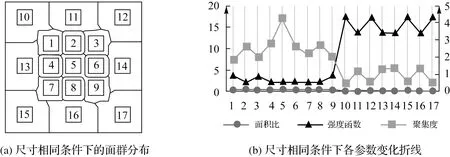
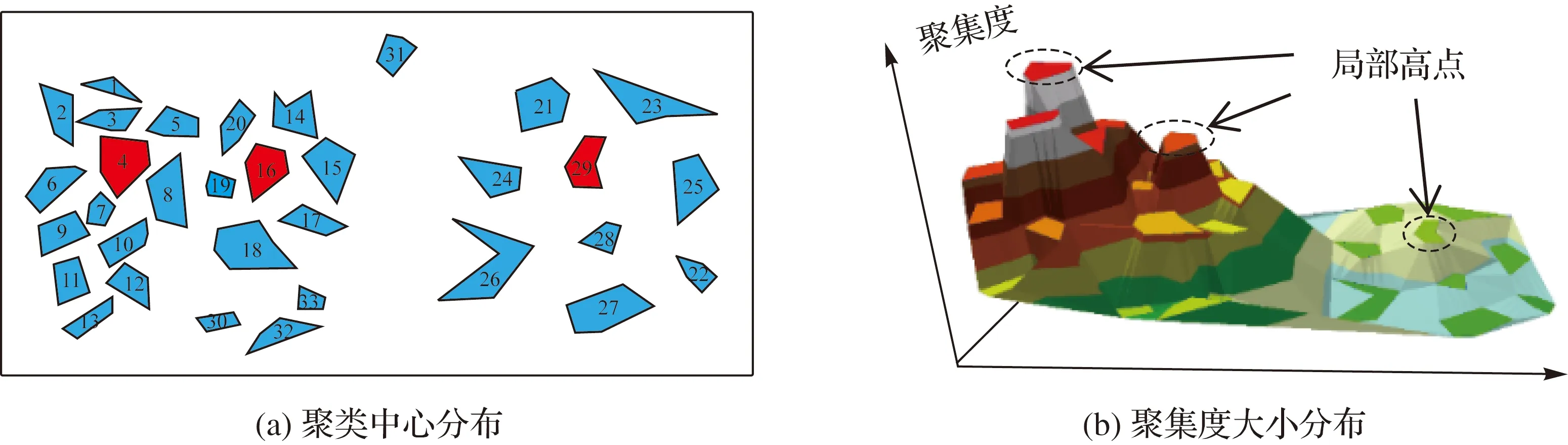
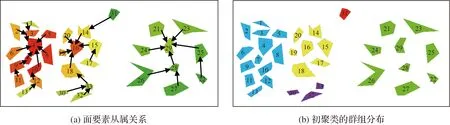
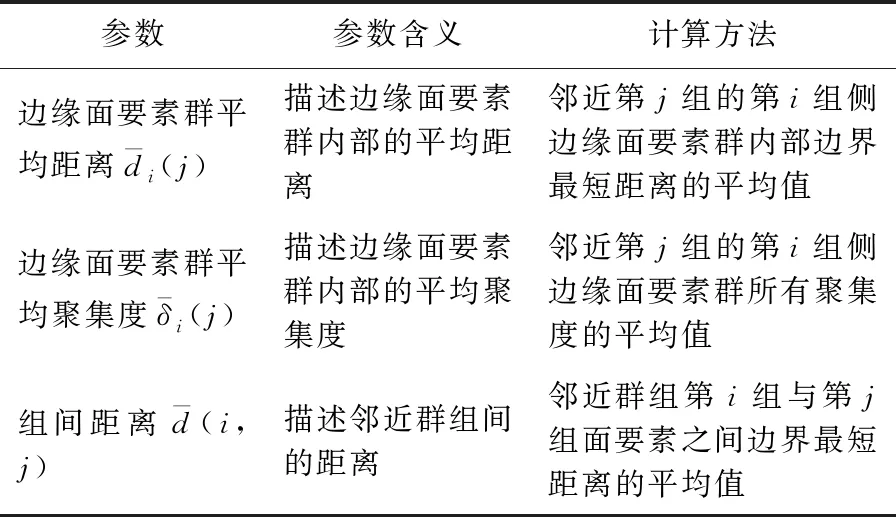
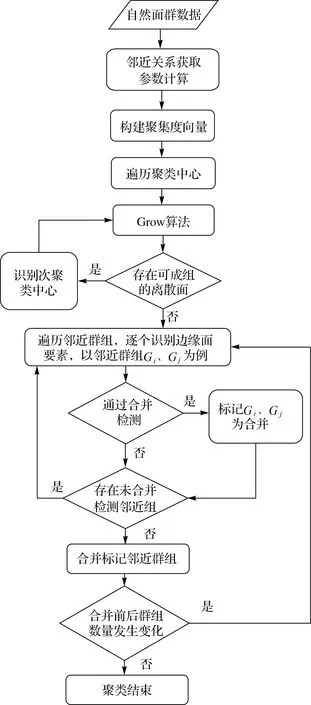
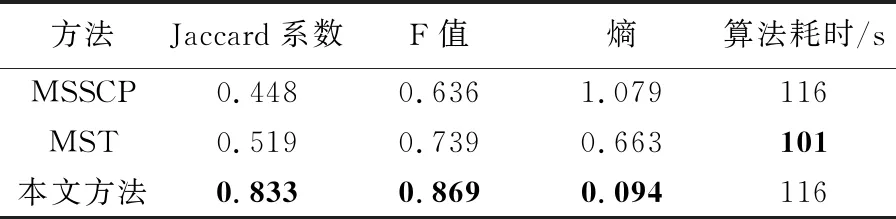
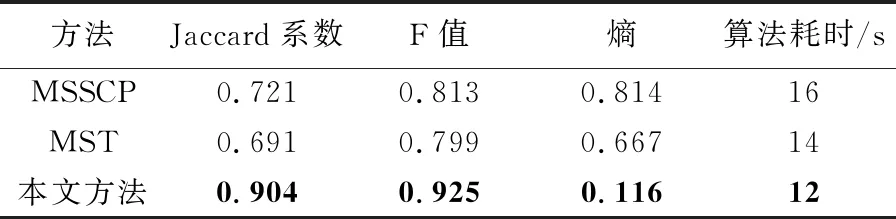
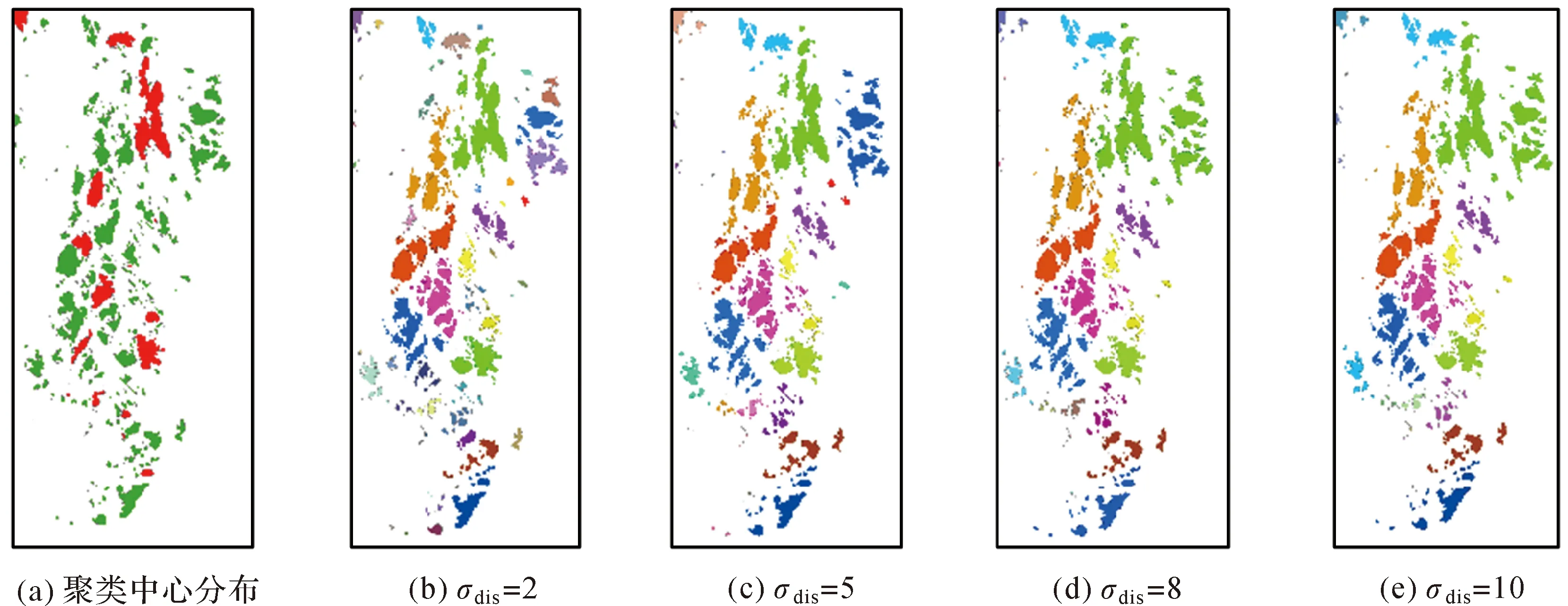
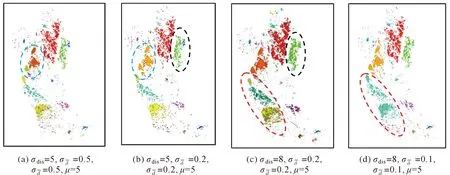
式中,φ(i)为面要素i的一阶邻近面要素及其本身;S(j)为面要素j的面积;Svor(j)为面要素j的Voronoi图面积;d(i,j)为面要素i与j的边界最短距离;dc表示截断距离,当d(i,j) (2) 图1 聚集度的计算Fig.1 Calculation of aggregation index 为验证“聚集度”的有效性,利用3种不同分布的面群数据进行测试,并引入2个描述面要素聚集程度的代表性参数,即“面积比”“强度函数”[14],对比分析不同参数对面群分布密度的度量能力,相关参数计算方法见表1。为区分三者结果差异,采用折线图进行比较,“面积比”和“强度函数”数值采用左坐标轴,“聚集度”数值采用右坐标轴。 表1 对比参数计算方法 (1) 面要素尺寸相同、邻近距离不同条件下的参数对比。如图2(a)所示,共有17个尺寸形状相同的正方形组成,其中1—9号分布集中、10—17号分布稀疏。如图2(b)所示,根据参数变化区间分为1—9号、10—17号两组。1—9号正方形“面积比”“强度函数”变化幅度小,未反映邻近面数量、邻近距离对分布密度的影响;“聚集度”变化幅度大,其中5号邻近面数量最多,边界最短距离均较小,“聚集度”最大;2、4、6、8号“聚集度”次之;1、3、7、9号邻近面数量少,边界最短距离最远,“聚集度”最小。10—17号正方形“面积比”相较于前组略有下降,未能体现分布密度变化;“强度函数”和“聚集度”均能清晰反映分布密度变化情况,面要素分布越稀疏,“强度函数”越大,“聚集度”越低。可见,在尺寸固定,邻近距离变化时,“强度函数”和“聚集度”均能反映面要素分布的疏密程度。特别的,尺寸与邻近距离均相同时,邻近面数量越多,本文“聚集度”区分性更强,有利于本文方法中聚类中心的识别,如图2(b)中的5号聚集度明显突出。 图2 尺寸相同条件下参数对比Fig.2 Parameters comparison under the same size condition (2) 面要素尺寸不同,邻近距离相同条件下的参数对比。如图3(a)所示,共有13个不同尺寸的正方形,相邻正方形邻近距离相同,1—13号尺寸逐渐增大。“面积比”随着面要素尺寸增大缓慢上升;“强度函数”基本保持不变;聚集度变化较大,6号聚集度全局最高,相较于3号,两者面要素数量相同,但6号邻域内面要素尺寸均大于3号,聚集度更大,8—13号“聚集度”波动下降,反映了边缘面分布密度整体下降的趋势。可见,“面积比”和“强度函数”描述面要素分布密度的能力较弱,且存在多个相同值,难以区分面要素分布密度差异。在邻近距离相同时,面要素尺寸越大、邻近面数量越多、邻近面尺寸越大,“聚集度”就越大,准确反映面要素分布密度差异,有利于聚类中心的识别及聚集度向量的构建。 图3 邻近距离相同条件下参数对比Fig.3 Parameters comparison under the same distance condition (3) 面要素尺寸与邻近距离均不同条件下的参数对比。如图4(a)所示,共有20个形状尺寸、邻近距离均不同的面要素,1—10号分布集中,11—20号分布松散。在第1组(1—9号)中,2、4号“面积比”较高,“强度函数”较低,“聚集度”较高,3个参数均能反映2、4号分布密度高的特点。在第2组(10—17号)中,“面积比”波动小,与第1组差异较小,不利于不同分布密度群组的分离;“强度函数”波动幅度大,但两组边缘面要素数值相近,例如6号与17号,不利于确定群组边缘面要素的归属;相较于第1组,第2组“聚集度”大幅降低,边缘面要素聚集度差异明显,有利于确定群组边界,同时16号“聚集度”局部最高,表明在面群松散时依然能够识别聚类中心。可见,在尺寸、邻近距离均不同的情况下,“聚集度”在反映面要素的分布密度方面更有优势,有利于实现不同分布密度面群的聚类。 图4 多差异条件下的参数对比Fig.4 Parameters comparison under the condition of multiple differences 综上所述,本文提出的“聚集度”能够准确描述面要素的分布密度,即面要素尺寸越大、邻近距离越小、邻近面数量越多、邻近面尺寸越大,面要素分布越密集,“聚集度”就越大,为本文聚类方法中描述自然面群的分布密度提供重要的参数依据。 根据自然面群的邻近性和密度相似性,本文围绕面要素聚集度和边界最短距离,提出了一种面向自然面群的聚类方法,主要包含以下3个环节:①聚类中心的识别;②基于聚集度向量的初聚类;③边缘检测与群组合并。 理想情况下,群组内分布集中、聚集度相近,且越接近群组中心,聚集度就越高,聚类中心就是群组内聚集度最大的面要素。然而实际情况下,一个视觉认知群组内往往存在多个聚集度为局部极大值的面要素,邻近面以其为中心聚集分布,形成面簇。通过识别这类面要素,就能将邻近面聚合成簇,达到初聚类目的。本文以一阶邻域作为识别范围,若面要素的聚集度均高于邻近面的聚集度,则该面要素被视为聚类中心。例如,图5共有28个形状尺寸各异,分布不均匀的面要素组成。根据式(1)计算聚集度构建分布图,得到处于“峰顶”的局部高点,即为聚类中心,如图5(b)所示。最终识别的聚类中心为4、16、29号。 图5 聚类中心的识别Fig.5 The identification of cluster center 定义1:聚集度向量。聚集度向量是面要素pi指向其一阶邻域内聚集度高于pi,且边界最短距离最小的面要素pj的组合,记为pi→pj,本文称之为pi从属于pj。 定义2:Grow算法。以群组{pi}中面要素pi为起点,获得其从属面集合{qj},按照边界最短距离由小至大读取。设置距离规则:①d(pi,qj) 除聚类中心外,每个面要素均能作为聚集度向量起点,指向高于自身聚集度的最近面要素,构成从属关系,如图6(a)所示,颜色越红则聚集度越大,越绿则聚集度越小,箭头为聚集度向量,起点为低聚集度面,终点为最近的高聚集度面,低聚集度面从属于高聚集度面,例如“1→3”为1号从属于3号,“1→3→4”为1号、3号均从属于4号。 根据聚集度向量,每个面要素均指向聚类中心,即局部区域的面要素均从属于该区域的聚类中心。那么,从聚类中心出发,沿着聚集度向量逆向搜索,局部区域内的所有面要素均可达。因此,将聚类中心作为群组的第1个对象,按序对每个加入群组的面要素执行Grow算法,构建初始群组。其中,距离规则①控制组内邻近面边界最短距离的上限,保证群组边界收敛;距离规则②控制组内邻近面边界距离的增长速度,防止距离突变导致离散面加入群组。如图6(b)所示,虽然存在“31→14”从属关系,但不满足距离规则①,31无法加入黄色群组;存在“33→18”从属关系,但不满足距离规则②,33无法加入黄色群组。 通过执行Grow算法,面要素围绕聚类中心构成面簇,但仍存在部分离散面要素,例如30—33。根据聚集度向量识别离散面要素的中心,作为“次聚类中心”,如图6(a)所示,30、32、33的次聚类中心为33。以次聚类中心为起点,执行Grow算法,直至无法形成新的聚类群组,则初聚类结束,初聚类结果如图6(b)所示。 图6 基于聚集度向量的初聚类Fig.6 Initial clustering based on aggregation index vector 初聚类根据聚集度向量将离散面要素聚合成簇,保证群组内分布紧密。然而,当面群分布密度不均匀时,一个视觉认知群组内易存在多个聚类中心,导致初聚类过度划分,不符合人类认知,如图6(b)中人工判读时,蓝色组、黄色组和紫色组应为一组,但由于存在多个聚集度中心,该组在初聚类中被划分为多个群组。为消除过度划分问题,本文设计邻近群组的边缘检测和合并策略,分为以下环节: (1) 边缘检测。根据面要素邻近关系,若存在pm属于群组Gi,pn属于Gj,且pm与pn相邻,则pm为Gi的边缘面,pn为Gj的边缘面,Gi与Gj相邻,如图7(a)所示,5与20相邻,则蓝色组与黄色组为相邻群组,红色虚线框内面要素为蓝色组和黄色组的边缘面。 图7 边缘检测与群组合并Fig.7 Edge detection and group merging 表2 边缘检测参数 (3) 群组合并。若邻近群组边缘面数量均大于1,且满足合并规则①②③,群组被合并;若存在邻近群组边缘面数量等于1,且满足合并规则②③,群组可被合并;否则邻近群组不合并。 为避免出现合并不充分问题,需对新合并群组再次进行边缘检测和群组合并,直至不存在需合并的邻近组,则聚类完成。如图7(b)所示,原蓝色组、黄色组、紫色组通过检测合并成一组,红色组31号面要素未通过检测不合并。 根据NPFC方法原理,本文设计如下实现流程,如图8所示。 (1) 拓扑关系获取与参数计算。据文献[24]方法,构建面要素的约束Delaunay三角网和Voronoi图,获取邻近关系。逐个计算邻近面的边界最短距离d(i,j),并得到截断距离dc,依照式(1)得到聚集度δ(i)。 (2) 构建聚集度向量,识别聚类中心。遍历所有面要素,以面要素pi为例,根据邻近关系和距离集合{d(i,j)}将邻近面要素由近至远排序;逐一读取邻近面pj,若δ(pj)>δ(pi),则构建聚集度向量pi→pj;若所有邻近面聚集度值均小于pi,则pi识别为聚类中心。 图8 NPFC方法流程Fig.8 Flow chart of NPFC method (3) 遍历所有聚类中心,以pi为例,初始化dmax=dc,对pi执行Grow算法,若有面要素加入,则更新dmax,并对其余面执行Grow算法,直至群组内不再有新面加入,则该步骤结束。 (4) 剩余离散面的聚类。遍历未加入群组的离散面,执行步骤(2),获取次聚类中心,并以次聚类中心为初始面执行步骤(3)。直至遍历完成,则初聚类结束。 (5) 边缘检测。遍历所有初聚类群组内面要素,根据面要素邻近关系获取群组邻近关系,识别邻近群组的边缘面,执行步骤(6)。 (7) 合并群组。若存在邻近组被标记为“合并”,则将所有标记的邻近组合并,并执行步骤(5);否则聚类结束,输出聚类结果。 NPFC方法具有以下优势:①设计的聚集度参数能够准确反映面要素分布密度,有利于根据分布疏密对面群聚类,符合人类认知。②兼顾面要素特征和群组整体特征,按照“局部→整体”的顺序实现聚类,有效克服了自然面群疏密程度不一导致聚类条件难以确定的问题。③采用邻近距离和分布密度的双重约束获取聚类结果,满足自然面群的制图要求,有利于后续对分布特征的挖掘。 为检验算法的有效性,本文选取自然面群的典型代表:岛屿群和自然湖泊群作为试验数据,按照试错法调整参数,得到聚类结果。 图9 岛屿群聚类过程Fig.9 The process of islands clustering 图10 湖泊群聚类过程Fig.10 The process of lakes clustering 试验区域自然面群聚集程度不一,局部区域存在多个聚类中心,导致初聚类后群组数量较多。通过边缘检测与群组合并后,群组数量明显减少,群组内面要素邻近距离变化和分布密度差异均处于视知觉的可接受范围内,符合人类认知。 为体现本文方法在处理自然面群聚类上的优势,选用MSSCP聚类方法[14]和基于边界最短距离的MST聚类方法进行对比试验。试验环境是Intel i7-1750 H,2.20 GHz处理器,Windows10操作系统。通过试错法调整参数,分别得到最优聚类结果。将试验结果与专业制图员的聚类结果进行对比,并采用Jaccard系数、F值、熵值[25-26]以及算法耗时作为聚类结果评价参数进行定量化评价。 以人工聚类结果为参照,选取MSSCP方法、MST方法和本文方法的试验结果进行对比,如图11所示,人工聚类共有83个群组;MSSCP方法循环次数为3次,共有117个群组;MST方法距离阈值为800 m,共有219个群组;本文方法参数设置与4.1节一致,共有193个群组。在MSSCP聚类结果中,蓝色虚线框内岛屿群未能按照分布轮廓进行聚类,这是由于两个群组之间的“通道”存在少量岛屿,MSSCP方法无法将其分离;黑色虚线框内岛屿群分布密度差异大,MSSCP方法和MST方法均无法对其进行有效分离;而本文方法对上述区域岛屿群均能有效分离,更接近人工聚类结果。 图11 不同方法的岛屿群聚类结果Fig.11 Island clustering results with different methods 参照人工聚类结果,分别计算上述3种聚类结果的定量评价指标见表3。在Jaccard系数、F值方面,值越大,说明与参照结果越相似;在熵方面,值越小,类归属的不确定性越低,与参照结果越相似。可见,本文方法在岛屿群聚类效果方面更具优势;在耗时方面,MST算法略快于MSSCP算法和本文算法。 表3 岛屿群聚类结果定量化评价 在对自然湖泊群进行聚类试验时,参照人工聚类结果,选取MSSCP方法、MST方法和本文方法的最优聚类结果,如图12所示。人工聚类共有30个群组,MSSCP方法循环次数为1次,聚类结果共有17个群组;MST方法距离阈值为500 m,聚类结果共有54个群组;本文方法参数设置与4.1节一致,聚类结果共有52个群组。对比人工聚类结果可以发现,在红框区域内,MSSCP聚类结果对群组的边缘面要素归属存在错误,如图12(g)所示,MST方法和本文方法结果与人工聚类结果接近;在黑框区域内,由于MSSCP方法对局部分布密度变化不敏感,MST方法无法感知局部分布密度差异,两者的聚类结果与人工聚类结果存在较大差异,如图12(h)、图12(j)所示,本文方法对局部距离和分布密度变化较为敏感,能够识别局部特征差异,与人工聚类结果更为接近。 图12 不同方法的自然湖泊群Fig.12 Lake clustering results with different methods 参照人工聚类结果,在Jaccard系数、F值方面,本文方法略高于其他方法;在熵方面,本文方法远低于MSSCP方法和MST方法,说明本文方法在自然湖泊群聚类方面存在优势;在耗时方面,本文方法略快于MSSCP方法和MST方法,见表4。 表4 湖泊群聚类结果定量化评价 为提高NPFC方法调节参数效率,以岛屿群局部区域为例,分析不同参数阈值对聚类结果的影响。在识别聚类中心的基础上,调整距离增长阈值σdis,得到不同聚类结果,如图13所示。σdis越小,群组数量越多,群组划分越细致;随着σdis增大,聚类的群组数量逐渐增大,但增长幅度放缓,并接近于聚类中心数量,如图13(d)、图13(e)初聚类结果基本一致。值得注意的是,σdis并非越小越好,需根据不同目标比例尺下最小感知阈值进行确定,在此给出参数调整的建议,即目标比例尺越大,聚类结果应越细致,σdis应减小;反之应增大。 图13 不同参数的初聚类结果Fig.13 Initial clustering results with different parameters 图14 不同参数的NPFC方法聚类结果Fig.14 Island clustering results with different parameters by NPFC 空间聚类能够挖掘自然面群的空间分布知识,是自然面群制图综合的重要步骤。针对自然面群几何差异大、分布整体分散、局部集中,且集中程度不一的特点,本文提出了一种自然面群的聚类方法。首先,定义一种面要素分布密度度量参数——聚集度,能较好顾及面要素自身尺寸、邻近距离、邻近面数量和邻近面尺寸对分布密度的影响;围绕聚集度和邻近距离设计了一种群组生长模型,能够以局部聚集度极大值面要素作为聚类中心,聚合邻近面;顾及群组邻近性和密度相似性,基于边缘聚集度和群组邻近距离提出了邻近群组的边缘检测和群组合并策略,有效解决了过度划分的问题。对比试验结果证明,聚集度能够准确地描述面要素分布密度差异;同时NPFC方法的自然面群聚类效果更好。 今后工作中需要进一步解决以下3方面的问题:①自然面群的制图综合,利用聚类结果提取的群组分布范围、密度差异等空间分布约束,更好地服务于自然面群的制图综合;②参数阈值设置的问题,研究参数阈值与比例尺的定量关系,得到目标比例尺下,人类视知觉对自然面群分布密度差异的最小识别阈值,并据此实现参数阈值的自适应调整;③本文方法对其他面群聚类问题的适用性。

1.2 指标对比分析



2 面向自然面群的聚类方法
2.1 聚类中心的识别
2.2 基于聚集度向量的初聚类
2.3 边缘检测与群组合并

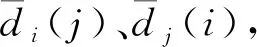
3 NPFC方法实现
4 试验与结果分析
4.1 试验过程


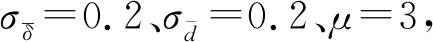

4.2 结果对比


4.3 参数分析

5 结 论

