Quantifying nonclassicality of multimode bosonic fields via skew information

Yue Zhangand Shunlong Luo

1 Beijing Academy of Quantum Information Sciences,Beijing 100193,China

2 State Key Laboratory of Mesoscopic Physics,School of Physics,Frontiers Science Center for Nanooptoelectronics,Peking University,Beijing 100871,China

3 Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China

4 School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

Abstract We quantify the nonclassicality of multimode bosonic field states by adopting an informationtheoretic approach involving the Wigner-Yanase skew information.The fundamental properties of the quantifier such as convexity,superadditivity,monotonicity,and conservation relations are revealed.The quantifier is illustrated by a variety of typical examples,and applications to the quantification of nonclassical correlations are discussed.Various extensions are indicated.

Keywords:Bosonic fields,nonclassicality,Wigner-Yanase skew information,multimode states,correlations

1.Introduction

While in the early days of its inception,quantum mechanics was also called wave mechanics,and quantum states were called wavefunctions [1],which highlighted the radical departure from the classical orbital reality of material motion,the situation is reversed in modern quantum optics,where classicality is more often related to wave nature,and nonclassicality (quantumness) is related to the particle nature of photons [2–7].The pursuit of nonclassicality leads to the emergence of quantum optics,with many theoretical predictions of the nonclassical properties of light (bosonic fields)such as squeezing,anti-bunching,sub-Poissonian statistics,Schrödinger cat states,etc.,all of which have been experimentally realized and have even found numerous applications in quantum information processing [2–10].

It is now widely recognized that the nonclassicality of bosonic field states is a fundamental part of quantum mechanics and a crucial resource in quantum practices,with extensive applications.Significant efforts have been made to detect and quantify the nonclassicality of states,and a variety of measures or quantifiers have been introduced.The first widely used quantity for characterizing the nonclassicality of light seems to be Mandel’s Q parameter [11],which used the deviation of the photon number from a Poissonian distribution to indicate nonclassicality.Various distance-based measures were introduced and studied in [12–19].Phase space distributions were exploited to characterize nonclassicality from many perspectives,such as nonclassical depth [20–23],measurable quadrature distributions [24,25],the negativity of phase space distributions [26–28],demarginalization [29].The negativity of normally ordered observables was investigated in [30].The moment method was invoked to characterize nonclassicality in [31,32].The conversion between nonclassicality and entanglement via beamsplitters led to the entanglement potential [33–35].Variance-based quantifiers were introduced in [36–38],and quantifiers based on the Wigner-Yanase skew information were elucidated in [39].All these quantifiers shed light on nonclassicality from different perspectives.

In this work,we will continue to pursue the information-theoretical approach to nonclassicality via the Wigner-Yanase skew information,as initiated in [39],in which only single-mode bosonic field states were treated and thus,within which,correlations could not be addressed.In multimode bosonic fields,the nonclassical effects become even richer due to the correlations among different modes.For example,if we have entangled multimode field states,we may expect stronger nonclassical effects.Here,we will extend the single-mode case to the multimode scenario,and further apply the quantifier of nonclassicality to study correlations.

Recall that in [39],an intuitive and simple quantifier for the nonclassicality of the single-mode bosonic field state ρ was introduced as

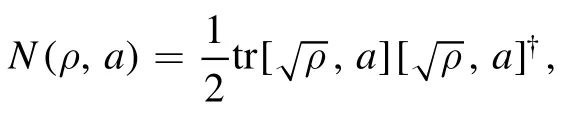
where a is the annihilation operator of the bosonic field satisfying the canonical commutation relation[a,a†]=1.The motivation for this comes from the remarkable Wigner-Yanase skew information [40,41]

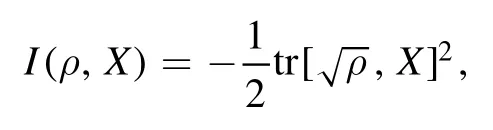
which quantifies the information content of the state ρ skew to the observable X.This concept gains more significance after it is recognized that the skew information realizes a kind of quantum Fisher information [42],and can be interpreted as the quantum uncertainty of X in the state ρ [43],as the asymmetry of ρ (relative to X) [44–47],and as the quantum coherence of ρ (relative to X) [48].

Now,if we rewrite the Wigner-Yanase skew information as

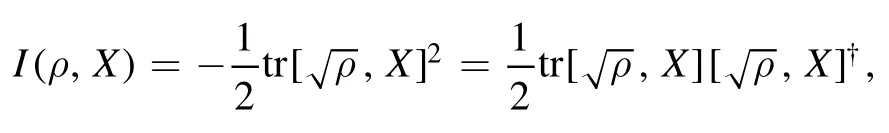
and replace the observable (Hermitian operator) X by the non-Hermitian annihilation operator a,we readily arrive at the quantityN(ρ,a) .Accordingly,the quantifier of nonclassicality may be interpreted as an extension of the celebrated Wigner-Yanase skew information to non-Hermitian operators.It turns out thatN(ρ,a)has a variety of remarkable properties which render it a useful quantity in studying nonclassicality,as elucidated in [39].

We emphasize that here,although the notion of nonclassicality is intimately related to the well-established optical nonclassicality in the Glauber-Sudarshan scheme,it actually goes beyond the latter framework,and should be understood in the general sense of quantum mechanics with its roots in the noncommutativity between operators.

The purpose of this paper is to extend the above quantifier of nonclassicality to the multimode scenario,and study its consequences and usage in assessing correlations.This paper is organized as follows.In section 2,for simplicity,we first treat the two-mode bosonic fields,introduce an information-theoretic quantifier of nonclassicality for bipartite states,and exhibit its fundamental properties.In particular,we establish a conservation relation for nonclassicality in beamsplitters.We work out a variety of examples to illustrate the concept in section 3.We employ the quantifier of nonclassicality to characterize correlations in section 4.Finally,we discuss multimode and other extensions in section 5.

2.Two-mode nonclassicality

Consider a two-mode bosonic field,shared by two modes(parties) 1 and 2,mathematically described by the field operator vectora=(a1,a2)of respective annihilation operators a1and a2of the two modes satisfying the canonical communication relations

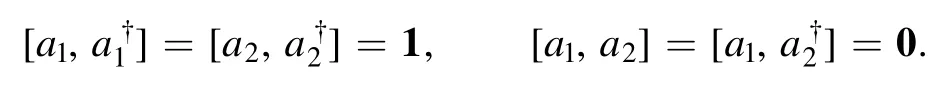
The coherent states of the two individual modes are the respective eigenstates of the corresponding annihilation operators:

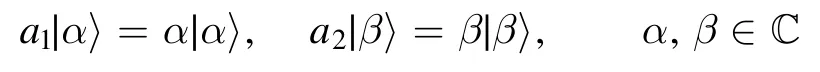
and the joint coherent states∣α〉 ⊗∣β〉 are regarded as the most classical (least quantum)two-mode pure states[49–52].Any two-mode bosonic field state described by a density matrix ρ can be completely characterized by its Glauber-Sudarshan P representation as [49–51]

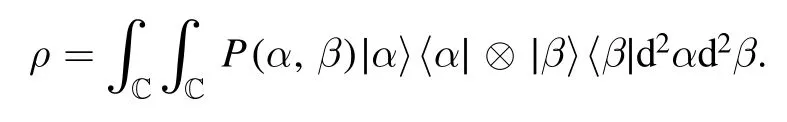
In general,the P functions may exhibit negativity or high singularity and thus fail to be probability distributions for certain states.In the customary treatment of quantum optics,those states with well-defined probability distributionsP(α,β)are defined as classical states (with respect to the coherent states),and all other states are termed nonclassical.Alternatively,the classical states are precisely probabilistic mixtures of coherent states.

For a two-mode state ρ,directly inspired by the singlemode information-theoretic quantifier of nonclassicality [39],we define

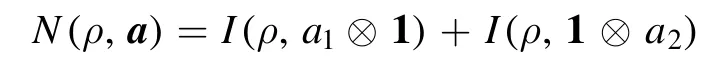
as a quantifier of nonclassicality for the bipartite state ρ,wherea=(a1,a2).More explicitly,we have

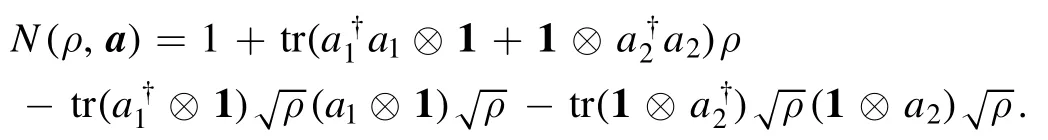
In particular,ifρ=∣Ψ〉〈Ψ∣is a two-mode pure state,then the above expression can be simplified as

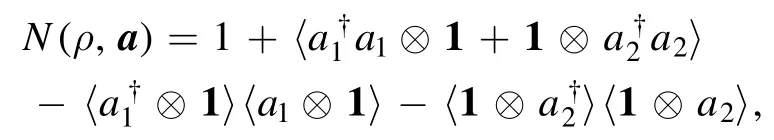
where 〈X〉= 〈Ψ∣X∣Ψ〉.

For any two-mode coherent stateρ=∣α〉〈α∣⊗∣β〉〈β∣,we haveN(ρ,a)=1,which is the minimal value of nonclassicality for two-mode pure states.Any other two-mode pure stateρ=∣Ψ〉〈Ψ∣satisfiesN(ρ)＞1.Thus,the coherent states have the smallest nonclassicality among all the pure states,in agreement with the fact that the coherent states are the most classical (least quantum) pure states.In contrast,for the two-mode Fock stateρmn=∣m〉〈m∣⊗∣n〉〈n∣,we haveN(ρmn,a)= 1+m+n,which shows that as the photon number increases,the nonclassicality increases,as expected.The Fock states are the most nonclassical states,in the sense that in the family of states ρ satisfyingthe Fock states∣n1〉 ⊗∣n−n1〉 ,n1=0,1,… ,n,achieve the maximal nonclassicality value 1+n.

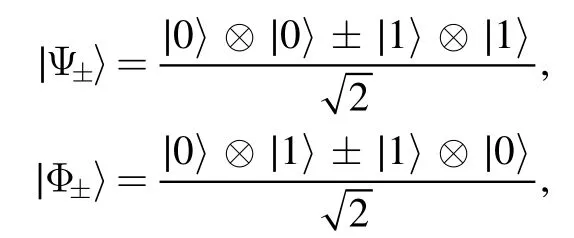
we haveN(∣Ψ±〉〈Ψ±∣,a)=N(∣Φ±〉〈Φ±∣,a)=2,while for the mixtures of Bell states

For the mixtureρ1=p∣Φ−〉 〈Φ−∣+(1 −p)∣0 〉 〈 0∣⊗∣0 〉 〈0∣of a Bell state and the two-mode vacuum state,we haveN(ρ1,a)= 1 +which is larger than 1 whenindicating nonclassicality in this case.For comparison,consider the superposition∣Φ〉=we haveN(∣Φ〉which is always larger than 1 whenp＞ 0.

The quantifier of nonclassicalityN(ρ,a) has a variety of equivalent expressions,which indicate its basic significance and potential applications.

First,it can be directly checked that

Second,let

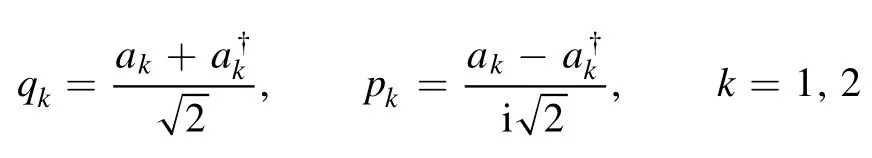
be the single-mode quadrature operators with[qk,pl]=iδkl,k,l=1,2,and

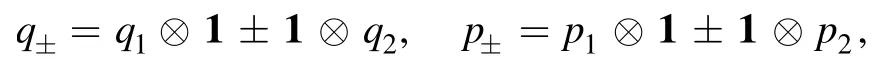
then

whereI(ρ,q1)=I(ρ,q1⊗1),etc.

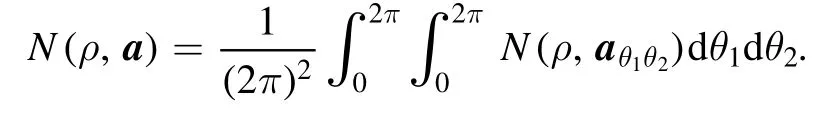
The quantifier of nonclassicalityN(ρ,a)has the following desirable properties.

(1) Convexity.For an ensemble of states{(pi,ρi)},it holds that

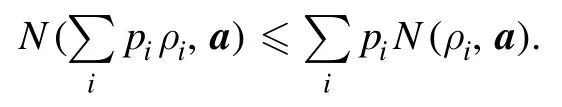
Consequently,if a state ρ satisfiesN(ρ,a)＞1,then it is nonclassical in the Glauber-Sudarshan scheme.This supplies a sufficient(though not necessary)criterion for detecting twomode optical nonclassicality.

(2) Superadditivity.It holds that

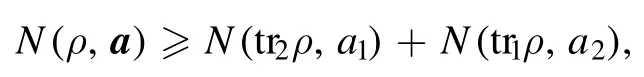
wheretr2ρis the reduced state of mode 1.The above inequality implies that global nonclassicality is larger than the sum of the local nonclassicalities,which is consistent with our intuition.

(3) Additivity for product state.For any product stateρ=ρ1⊗ρ2,it holds that

Moreover,by convexity,for any separable stateit holds that

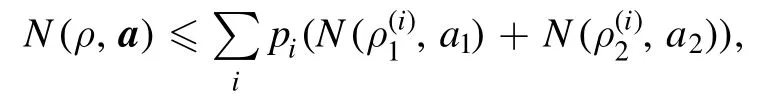
which may be exploited to derive some criteria for detecting entanglement.

(4) Displacement invariance.For the two-mode phase space displacement operators

it holds that

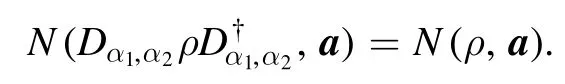
(5) Rotation invariance.For the two-mode phase space rotation operators

it holds that

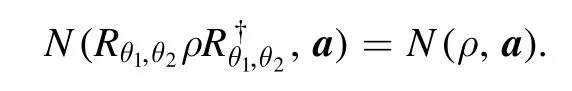
(6) Nonclassicality conservation via beamsplitters.For the beamsplitter transformationand any two-mode product stateρ=ρ1⊗ρ2,it holds that

(7)Nonclassicality enhancement via squeezing.For twomode squeezing

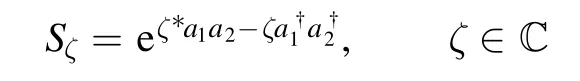
and any two-mode product stateρ1⊗ρ2,it holds that

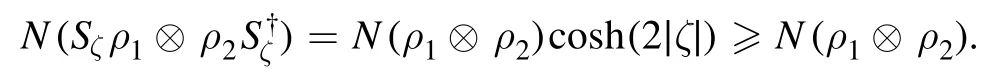
The proof of the above properties is straightforward.Item(1) follows from the convexity of the skew informationI(ρ,X)[40].Item (2) follows from

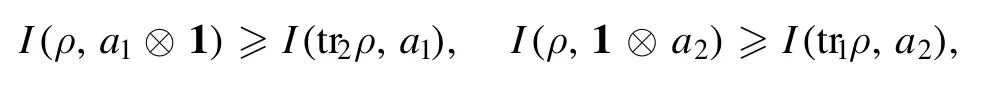
which in turn are implied by the monotonic inequalityI(ρ,K⊗ 1) ≥I(t r2ρ,K)[41].Items (3)–(7) can be readily verified by direct manipulation of the definitionN(ρ,a)=I(ρ,a1⊗ 1)+I(ρ,1⊗a2).

3.Illustration

In order to gain a more intuitive understanding of the quantifier of nonclassicality and to illustrate its characteristic features,we now work out some typical examples.

Example 1.For the separatively squeezed coherent state

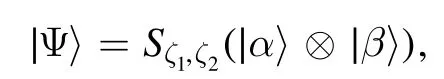
we have

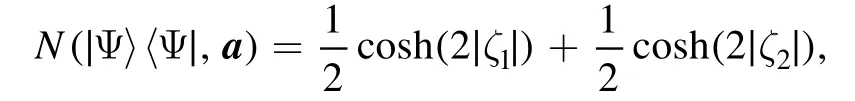
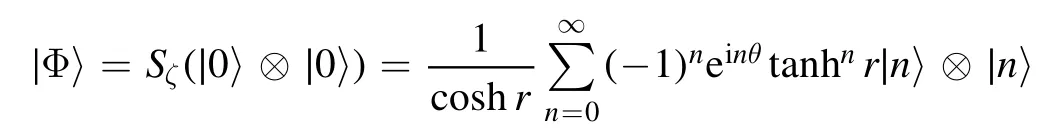
withζ=reiθ,r＞0,we have

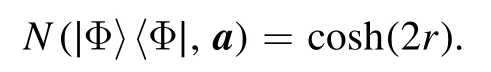
Example 2.For the two-mode thermal states

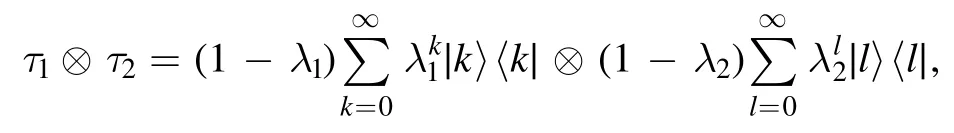
which are the product states of two single-mode thermal states with parametersλ1,λ2∈ (0 ,1) ,respectively,we have

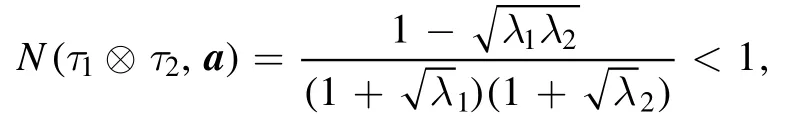
which decreases inλ1orλ2and shows that the two-mode thermal states are classical.In sharp contrast,for

we have

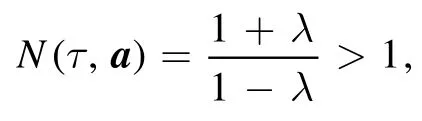
which is an increasing function ofλ.

Example 3.For two-mode Gaussian states of the form

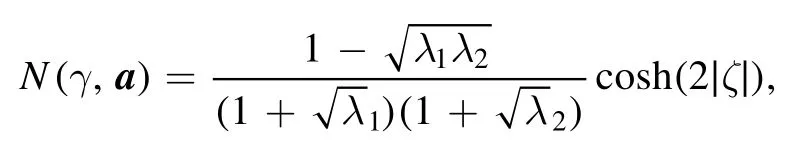
which shows that the nonclassicality is an increasing function of the squeezing strength∣ζ∣,while for the product states of the two single-mode Gaussian states

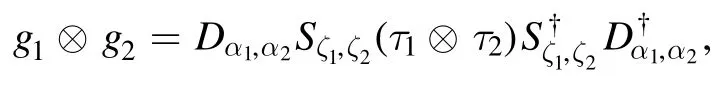
we have

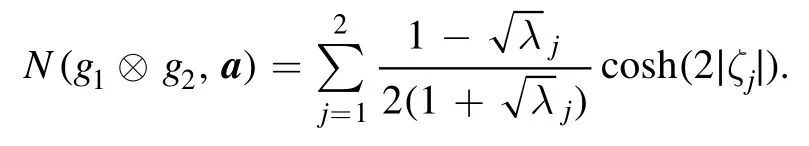
Let

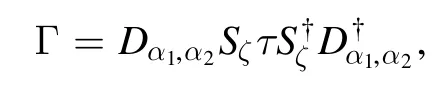
In sharp contrast,for states of the form

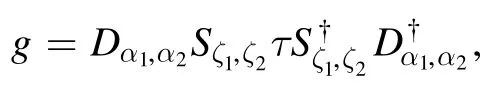
we have

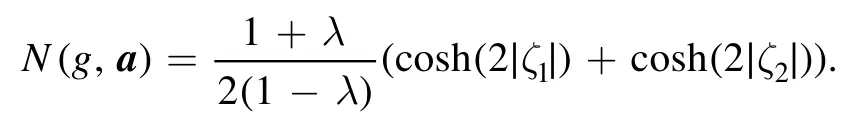
Example 4.Forwe have

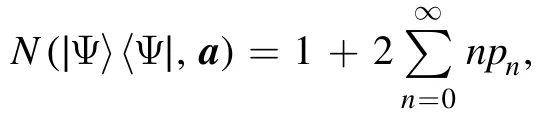
which can equally be expressed as

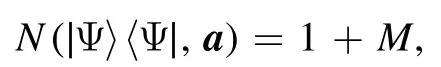
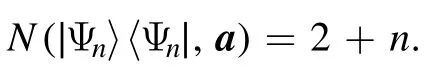
In contrast,for the Fock-diagonal state

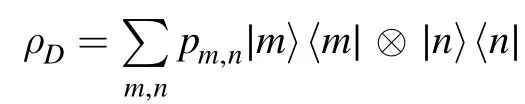
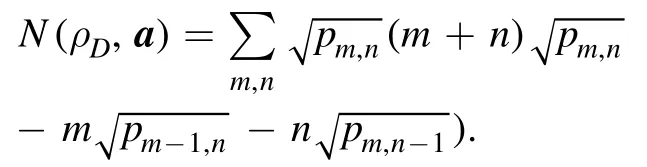
In particular,for the stateswe have

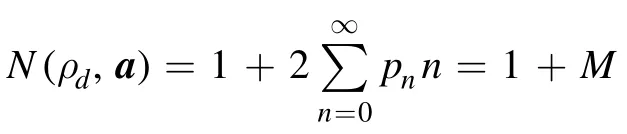
Example 5.Consider a spin-j system,embedded as a(2j+1) -dimensional subspace of the two-mode bosonic field via the Schwinger realization

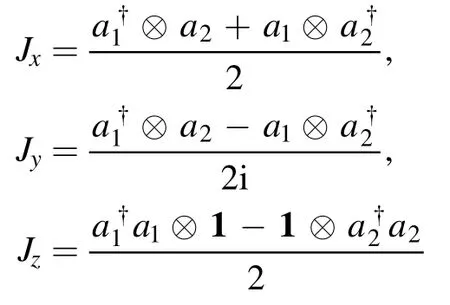
of the SU(2) Lie algebra

Let

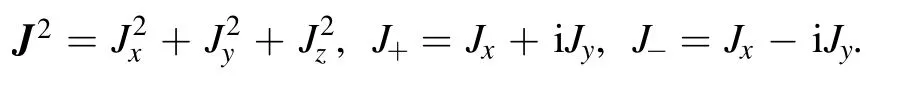
The Dicke states

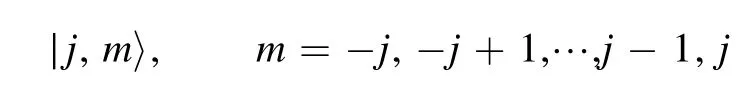
as the common eigenstates of the commuting operatorsJ2and JzsatisfyingJz∣j,m〉=m∣j,m〉,J2∣j,m〉=j(j+1)∣j,m〉,correspond to the two-mode Fock states

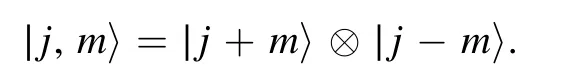
Moreover,

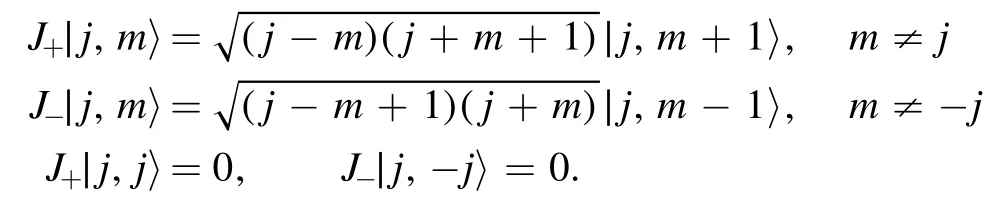
It follows that

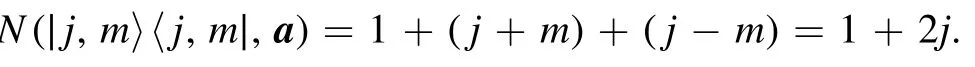
The spin coherent states

can be expressed in the Dicke basis as

and we have

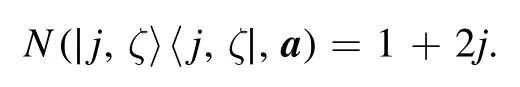
Actually,for any superposition of the Dicke states (thus any pure state of the spin-j system)

we have

For any mixture of the Dicke states

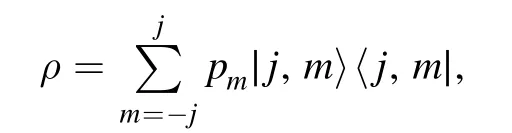
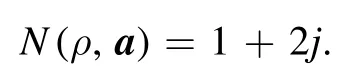
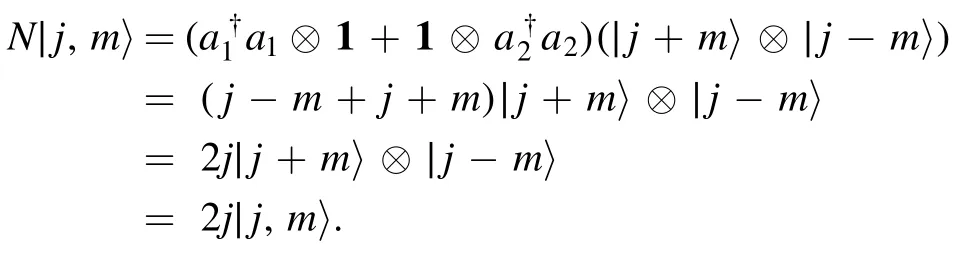
This is independent of m,and implies that for any pure spin-j state∣Ψ 〉=it holds thatN∣Ψ 〉= 2j∣Ψ〉.Consequently,the total photon number is conserved in the spin-j system.The spin-j system Hilbert space Hjis the eigenspace of the total number operator N with eigenvalue2j,and the two-mode bosonic system Hilbert space H is orthogonally decomposed as

withH0= C.This explains why all spin-j system pure states have the same nonclassicality 1 +2j: they are states with a total photon number of2j.This example shows that the quantifier of nonclassicalityN(ρ,a) cannot distinguish states in the same spin-j system,and captures the idea that nonclassicality is related to the precise number of photons.

4.Correlations

We wonder whether the difference between two-mode nonclassicality and local nonclassicalities can be used to capture correlations between the two modes.For this purpose,let us introduce

It is obvious that for any product statesρ1⊗ρ2,we have

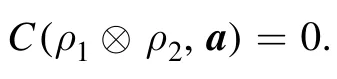
Just like the quantum mutual information,which is used as a standard measure for correlations,the quantityC(ρ,a)is neither convex nor concave inρ.To see this,noting that for any separable statewe haveC(ρ,a)＞0 whilewhich shows thatC(ρ)is not convex.On the other hand,let S (ρ1,ρ2)={ρ: tr2ρ=ρ1,tr1ρ=ρ2} be the set of two-mode states whose reduced states are fixed asρ1andρ2,then clearly this set is convex,andC(ρ,a)is convex on this set,indicating thatC(ρ,a)cannot be concave.Consequently,C(ρ,a)is indeed neither convex nor concave inρ.

Let us further consider some typical examples.

(1) For the mixture states

with reduced states

we have

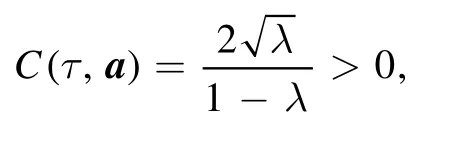
which is an increasing function ofλ.

(2) For the Bell states∣Ψ±〉 ,∣Φ±〉,we have

(3) For the two-mode squeezed vacuum statewe have

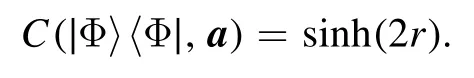
It is interesting to compare this quantity of correlations with entanglement,as quantified by the marginal von Neumann entropy

of the reduced states ρ1= tr2∣Φ〉〈Φ∣,ρ2= tr1∣Φ〉〈Φ∣.Both are monotonic and increasing functions ofr.

(4) We now consider the correlations generated by beamsplitters in terms of nonclassicality.Recall that a typical beamsplitter transformation sending the input two-mode field a=(a1,a2)to the output two-mode field b=(b1,b2)is implemented byvia [53]

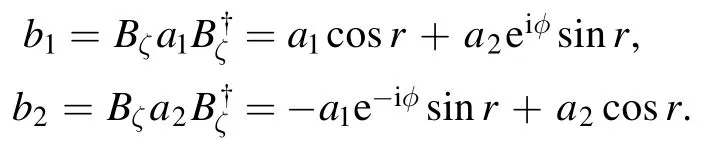
Since

Considering the situation of a balanced beamsplitterif the single-mode input states are squeezing vacuum statesthen we have

If the input two-mode state isρ=∣n〉 ⊗∣0〉 for the balanced beamsplitter,then

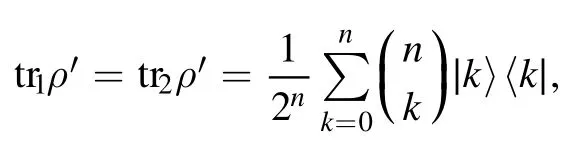
and we have

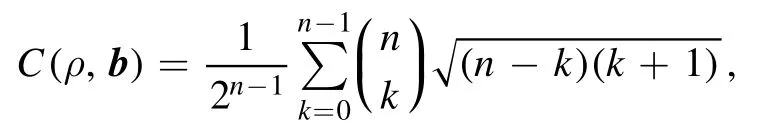
which shows that nonclassical correlations are generated via the beamsplitter since

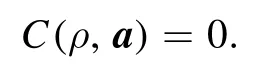
5.Discussion

Inspired by an information-theoretical quantifier of the nonclassicality of single-mode bosonic field states,we have introduced a quantifier of nonclassicality for two-mode bosonic field states,which can be naturally generalized to multimode bosonic fields as

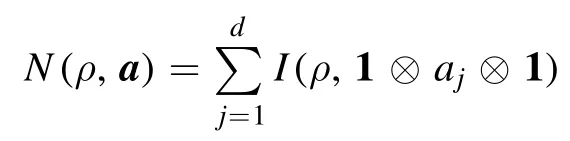
with the mode-annihilation operators of the d-mode bosonic field aj,j= 1,… ,d ,and a=(a1,… ,ad).We have further revealed its basic properties,elucidated its various features,and explicitly worked out several examples to illustrate its significance and intuitive meaning.We have also applied the nonclassicality to the quantification of correlations.It may be interesting to seek further applications of the results in concrete physical systems.

Though the present two-mode quantifier of nonclassicality,which does not involve any optimization,is easy to calculate,it only captures some special features of nonclassicality.To gain a more complete picture,we may consider more quantities.

(1) To distinguish the nonclassicality of states with a conserved total photon number,we may introduce

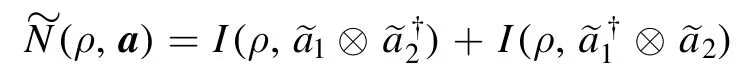
(2) To distinguish the nonclassicality of states generated by{∣n 〉 ⊗∣n 〉 ,n=0,1,… },we may introduce

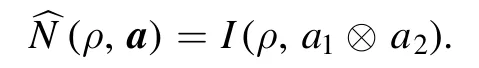
(3) Moveover,we may generalize N (ρ ,a)by considering the quantity

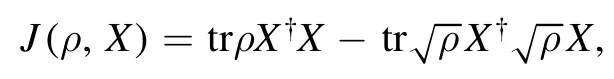
which yields a family of quantifiers of two-mode nonclassicality

parameterized by r=(r1,r2),rj=1,2,…

Together,these quantifiers can capture more aspects of nonclassicality,and further characterize correlations by the means given in section 4.

Nonclassicality in multimode bosonic fields exhibits many new effects due to the interaction between different modes,and it is desirable to further explore the interplay between nonclassicality and correlations in order to obtain a deeper understanding of the fields.

Acknowledgments

This work was supported by the National Key R&D Program of China,Grant No.2020YFA0712700,and the National Natural Science Foundation of China,Grant Nos.11 875 317 and 61 833 010.

ORCID iDs