Spatial-dependent probe transmission based high-precision two-dimensional atomic localization
Muhammad Idrees,Humaira Kalsoom,Bakth Amin Bacha,Arif Ullah and Li-Gang Wang
1 Zhejiang Province Key Laboratory of Quantum Technology and Device,Department of Physics,Zhejiang University,Hangzhou 310027,China
2 Quantum Optics and Quantum Information Research Group,Department of Physics,University of Malakand,Chakdara Dir(L),Khyber Pakhtunkhwa,Pakistan
3 Department of Mathematics,Zhejiang Normal University,Jinhua 321004,China
Abstract Herein,we propose a scheme for the realization of two-dimensional atomic localization in a λ-type three-level atomic medium such that the atom interacts with the two orthogonal standing-wave fields and a probe field.Because of the spatially dependent atom-field interaction,the information about the position of the atom can be obtained by monitoring the probe transmission spectra of the weak probe field for the first time.A single and double sharp localized peaks are observed in the one-wavelength domain.We have theoretically archived high-resolution and high-precision atomic localization within a region smaller than λ/25×λ/25.The results may have potential applications in the field of nano-lithography and advance laser cooling technology.
Keywords:2D atomic localization,probe transmission spectra,standing-wave fields,three-level atomic medium
1.Introduction
It is witnessed by the last few decades that the precise atomic position measurement,dubbed as atomic localization,has been an active research area both from experimental as well as theoretical points of view [1–6].Atomic microscopy has been extensively scrutinized due to its wide range of applications in numerous areas,including atomic nano-lithography [7,8],Bose–Einstein condensation [9],neutral atoms laser cooling and trapping [10,11].Atoms have been previously localized by some groups in a cavity based on optical virtual Slits[12–15].The atomic localization probability can be measured by scoping the optical field phase shift though the atom-field interaction.Quantum interference and atomic coherence effects are significant in the phenomena like electromagnetically induced transparency [16],giant Kerr nonlinearity [17,18],emission enhancement or suppression [19–21],four-wave mixing [22],and spontaneous optical bistability [23,24].
Based on quantum interference and atomic coherence effects,several one-dimensional (1D) atomic localization schemes have been introduced [25–30].For instance,Herkommer et al used the Autler–Townes spontaneous spectrum and observed 1D atomic localization[27].Likewise,Paspalakis et al also localized the atom in a three-level atomic configuration using the weak probe field and classical standing waves [28,29].Similarly,atoms have been localized in a ladder-type four-level atomic configuration via quantum interference,see [30].Also,Sahrai et al and Kapale et al have used the absorption spectrum as a phase and amplitude controller in 1D atomic localization[31,32].Additionally,atoms can be localized in a single dimension using dual resonant superposition [33],coherent population trapping or dark resonance [34–36].Recently,two standing-wave superposition has been used in a Λ-type 1D atomic system for the measurement of the atomic localization[37].Moreover,surface plasmon-induced atomic localization has also been examined in a tripod-type atomic system [38].
More recently,two-dimensional(2D)atomic localization has become an active research area [39–48].In this respect,Wan et al have performed 2D atomic localization via Y-type four-level atomic system and localized the atom in a region of λ/2×λ/2 with 25% localization probability [39].Li et al have introduced a four-level Λ-type atomic system for 2D atomic localization via radio frequency driven field through a phase-sensitive absorption spectrum [40].Moreover,Ding et al have also investigated 2D localization in a microwavedriven four-level atomic system[41].They have localized the atom in a region of λ/2×λ/2 via probe absorption with 100%localization probability.Similar 2D schemes have been used for the atomic localization through spontaneous emission [42,43],gain absorption spectra [44–46],and level population measurement[47,48].Further advancement in the field of atomic localization has been made by [49–58].
Inspired by these studies,we proposed a λ-type threelevel atomic system to examine more precise 2D atomic localization through probe transmission spectra of the weak probe field.Atom localization in a region smaller than λ/25×λ/25 is observed that yielded a high-resolution and highprecision atomic localization with maximum probability.When an atom passes through the 2D standing waves,the light-atom interaction becomes spatially dependent on the 2D space due to position-dependent Rabi frequencies of the standing wave’s fields.The transmission probability could become maximal in those regions where the atom passes through,that is,λ/25×λ/25,whereas it remains‘0’over the rest of the 2D space.This work is organized as follows;section 2 presents the proposal,including the model system and its dynamics.Section 3 contains numerical results and discussion regarding the 2D atomic localization.Finally,the work is summarized in section 4.
2.The model system and its dynamics
In this case,we consider a λ-type three-level atomic medium as depicted in figure 1.In this atomic configuration∣1〉 and∣2〉are the ground states while∣3〉 is the excited state.The probe field with Rabi frequency Ωp(transition frequency ω31)drives the transition between levels∣1〉 and∣3〉 .Similarly the transition between levels∣2〉 and∣3〉 is driven by the controlled field (standing wave field) having Rabi frequency Ωc(x,y)(transition frequency ω32).The 2D standing-wave field with Rabi frequency Ωc(x,y)is the superposition of two orthogonal standing waves along the x and y directions,written as
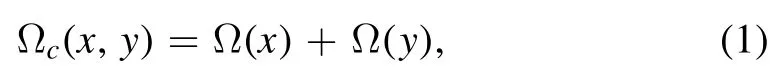
where
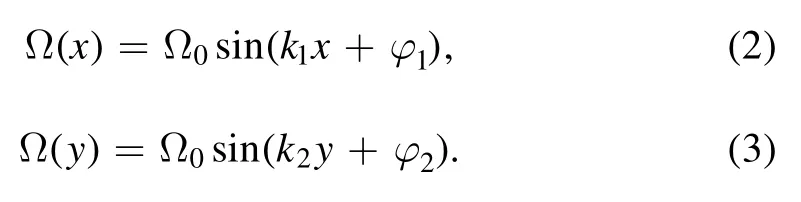
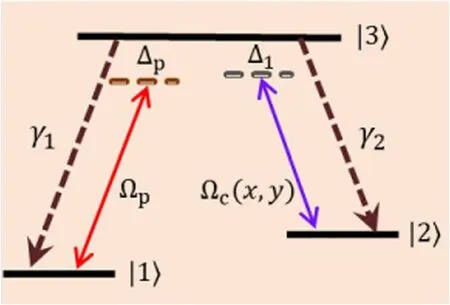
Figure 1.Schematic diagram of three-level λ-type atomic medium(87Rb).The parameters Ωp and Ωc(x,y) correspond to the Rabi frequencies of the probe and standing wave fields respectively,while γ1 and γ2 are the atomic decay rates.
The parameter Ω0indicates the amplitude of Ω(x) and Ω(y),where φ1,φ2and ki=kηi(i=1,2)are the corresponding phase shifts and wave vectors associated with the standing-waves,respectively.The parameters k=2π/λ,η1= cosθxandη2= cosθyrepresent the magnitude and directions of the wave vector associated with standing wave fields along the x and y directions respectively.If ηi(i=1,2)are 1 or −1,we observed the symmetric superposition effect of the standing-waves.For the range −1 <η1,2<1,an asymmetric superposition,play a vital role in the localized peaks evolution within a region for −π ≤kx ≤π and −π ≤ky ≤π in 2D space.For 2D atomic localization the decay rate for the excited state∣3〉 is chosen to be γ=2π×6.07 MHz (the natural line-width of87Rb of D2line).In the following numerical results,all the parameters were scaled with γ.The spatial-dependent interaction of standing waves and atoms on 2D space is already understood.When the atom passes through the standing waves,it encounters position-dependent Rabi frequencies of the standing waves.
We assume that the energy of atomic interaction is larger compared to the kinetic energy,therefore the center-of-mass position of the atom through the standing-wave does not change during the interaction time (according to the Raman–Nath approximation),and the kinetic energy part of the Hamiltonian is ignored.Under the rotating wave approximation,the Hamiltonian for the proposed atomic medium reads [59]
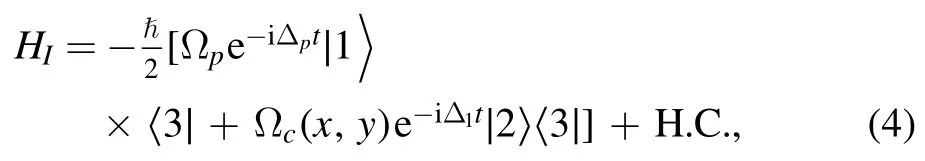
where the Hermitian conjugate term is given by H.C.,and the detuning of the fields are Δp=ω13−ωpand Δ1=ω23−ωc.To describe the dynamics of the given atomic system,the density matrix equation is given as [60,61]
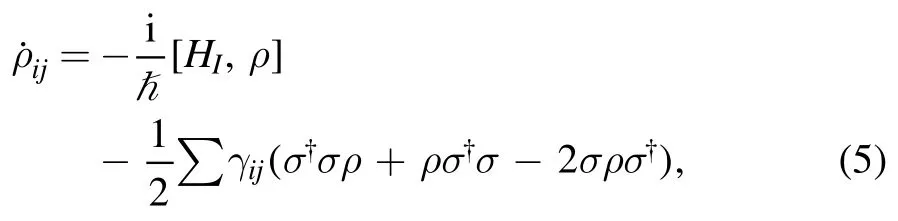

Figure 2.Probability distribution W(x,y)as functions of(kx,ky).The general parameters are γ=2π×6.07 MHz,Ω0=10γ,γ1=γ2=0.2γ,Δ1=0γ,Δp=10γ,φ1=φ2=0.(a) η1=1,η2=1,(b)η1=−1,η2=1,(c) η1=0.8,η2=0.6,(d) η1=−0.8,η2=−0.6.
where HIrepresents the interaction Hamiltonian,the atomic decay rate is represented by γijand the raising and lowering operators are denoted by σ†and σ,respectively.
On the basis of the Hamiltonian (equation (4)) and density matrix equation(5),we obtain the equations of motion for the transitions of given atomic medium.To find out the density matrix element(which gives information about the atomic localization),we use the following rate equations:
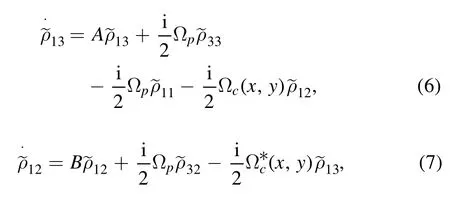
where

We consider that the probe field intensity is much weaker as compared to the other given laser fields (i.e.Ωp<<Ωc(x,y)),and almost all the atoms are populated in the ground stateTherefore,using the approach of perturbation,we can obtained the solution of the steady-statefrom equations (6) and (7)
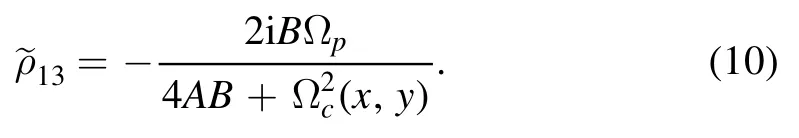
As we know that the position-dependent optical susceptibility is directly proportional to the translation elementtherefore the optical susceptibility is given as [62,63]
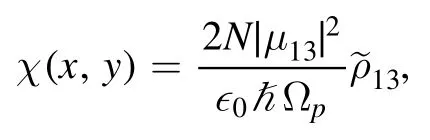
where N expresses the atomic density,μ13represents the dipole matrix element of the levels∣1〉 and∣3〉 ,while ∊0and ħ stand for the permittivity of free space and reduced plank’s constant,respectively.Usingthe optical susceptibility of the proposed three-level atomic system is given as
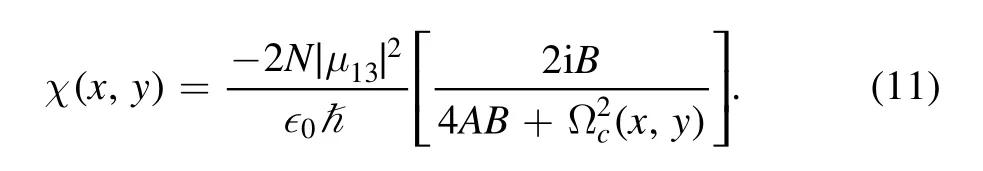
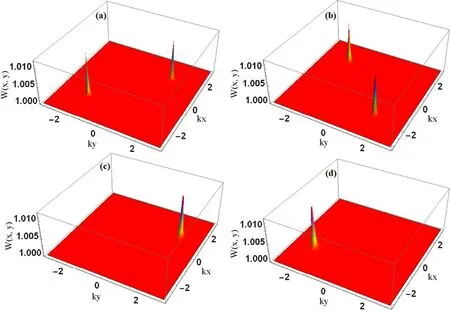
Figure 3.Probability distribution W(x,y)as functions of(kx,ky).The general parameters used are γ1=γ2=0.01γ.All other parameters have same values as in figure 2.
Equation (11) represents the 2D position-dependent susceptibility of the three-level λ-type atomic medium.
The propagating probe beam can be absorbed,reflected and transmitted through the cavity.Here we are intrusted in the transmission spectrum of the probe field,can be written as[64]
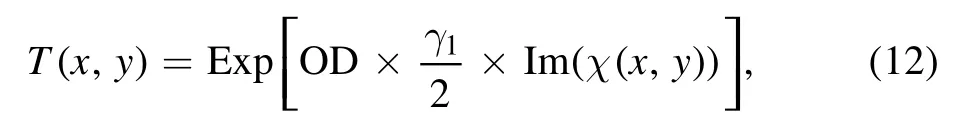
where OD=3NLλ2/2π is the optical depth of the cavity,L is the length of the cavity,and λ is the wavelength of the probe field.
3.Results and discussion
We analyze the numerical results for 2D atomic localization in one-wavelength domain based on equation(12)by adjusting the system parameters.The selected parameters comprise ħ=1.05×10−34J·s,∊0=1.054×10−12N·m2·C−2,and N=2×1017m−3.In figure 2,the probability distribution,(W(x,y)∝T(x,y))is plotted as a function of(kx,ky)in one-wavelength domain.This gives us the information about the atomic localization through the transmission profile of the probe spectrum.Here,it can be seen that both the precision and the spatial distribution of 2D atomic localization are very sensitive to the symmetric and asymmetric superposition of the standing wave fields.When the symmetric superposition of the standing wave fields occurred due parallel propagation of standing wave fields in the 2D space (η1=1 and η2=1),we observed two localized peaks located at I and III quadrant as shown in figure 2(a).The maxima of transmission appear at those points where the existence probability of the atom is maximum under the appropriate condition of symmetric superposition.When the phenomena of the symmetric superposition of the standing wave fields appeared due to antiparallel propagation of the standing wave fields (i.e.η1=−1 and η2=1),the localized peaks are shifted into II and IV quadrant respectively,as shown in figure 2(b).Since asymmetric superposition of the standing wave fields plays a key role in further improvement of the spatial resolution and precision of the atomic localization (for the range −1 <η1,2<1,an asymmetric superposition,comes into play a vital role in the localized peaks evolution within a region for −π ≤kx ≤π and −π ≤ky ≤π in 2D space).When the asymmetric superposition of the standing wave fields occur(η1=0.8 and η2=0.6)in the x–y plane,we get a single localized peak,which manifests the probe field transmission to occur at a single point.The localized peak exists in the quadrant I of the 2D space as shown in the figure 2(c).When the phenomena of the asymmetric superposition of the standing wave fields appeared due to reversed directions of the wave vectors (i.e.η1=−0.8 and η2=−0.6)while all the other parameter are fixed,the localized peak shifts to quadrant III,as shown in the figure 2(d).
To explicitly show the high resolution and high precision atomic localization through the transmission probe spectrum,we modify the 2D atomic localization behaviors as shown in figure 3.The influence of the decay rates (γ1,2) plays an important role in the modification of 2D atomic localization.With decreasing decay rates from 0.2γ to 0.01γ (keeping all other parameters fixed),two sharp localized peaks were investigated in the 2D space located in the I and III quadrant and II and IV quadrant as shown in figures 3(a) and 3(b),respectively under the symmetric superposition of standing wave fields.Moreover,we also investigate a sharper single localized peak in the 2D space in the I and III quadrant under the effect of asymmetric superposition of the standing wave fields as shown in figures 3(c)and(d)respectively.In this case,we get high-resolution and high-precision atomic localization in 2D space via probe transmission and the conditional position probability is maximum a specific point,which infers that the atom is completely localized in a region smaller than λ/25×λ/25,with a localization probability is greatly improved at a particular position.Even more,some authors have reported similar maximum probability (100%) in a region with area of λ/2×λ/2 and λ/10×λ/10,respectively,both of which are larger than in our case [65,66].Our work is a theoretical proposal for localizing the atom,and it provides a suggestion to possibly observe the localization of atoms in such 2D space.
4.Conclusions
In summery,we have studied the 2D atomic localization in a λ-type three-level atomic medium via probe transmission spectra of the weak probe field.The behavior of the 2D localization is observed to be significantly improved up to high-precision and high-resolution.The influence of the symmetric and asymmetric superposition of standing wave fields play a key role in the evolution of the localized peaks within a region of −π ≤kx ≤π and −π ≤ky ≤π in 2D space.More efficient double and a single sharp localized peaks are observed in single wavelength domain.We have theoretically induced more precise atomic localization within a region smaller than λ/25×λ/25.Finally,it should be noticed that our studies could be helpful in many applied physics including nano-lithography,lasercooling and trapping of neutral atoms,and so on.
Acknowledgments
This research is supported by the Zhejiang Provincial Natural Science Foundation of China under Grant No.LD18A040001,the National Key Research and Development Program of China (No.2017YFA0304202),and the National Natural Science Foundation of China (Grant No.11974309).
 Communications in Theoretical Physics2021年4期
Communications in Theoretical Physics2021年4期
- Communications in Theoretical Physics的其它文章
- Charged torus-like black holes as heat engines
- Pure annihilation decays of and in the PQCD approach
- Exploring the latest Pantheon SN Ia dataset by using three kinds of statistics techniques
- Hawking temperature of Kerr anti-de-Sitter black hole affected by Lorentz symmetry violating*
- The vacancy defects and oxygen atoms occupation effects on mechanical and electronic properties of Mo5Si3 silicides
- Deposition pattern of drying droplets
