Two model equations with a second degree logarithmic nonlinearity and their Gaussian solutions

Cheng-Shi Liu

Department of Mathematics,Northeast Petroleum University,Daqing 163318,China

Abstract In the paper,we try to study the mechanism of the existence of Gaussian waves in high degree logarithmic nonlinear wave motions.We first construct two model equations which include the high order dispersion and a second degree logarithmic nonlinearity.And then we prove that the Gaussian waves can exist for high degree logarithmic nonlinear wave equations if the balance between the dispersion and logarithmic nonlinearity is kept.Our mathematical tool is the logarithmic trial equation method.

Keywords: Gaussian solitary wave,Gausson,logarithmic nonlinearity,wave equation,trial equation method

1.Introduction

Gaussian waves which include Gaussian solitary wave and Gausson[1,2],are different to the solitons like sech-function solution in integrable systems.Among those,Gaussian solitary wave is for real equations,while Gausson is for complex equations.Due to the pulse shape,and the shape of Gaussian wave being invariant by the balance between dispersion and logarithmic nonlinearity,some researchers are attracted to study this kind of wave equations from several aspects,such as the constructions of Gaussian solitary waves,stability of solutions,and dynamics of wave propagation and so on.

In 1976,Bialynicki-Birula and Mycielsk[3]proposed the following first degree logarithmic nonlinear Schrödinger equation (LNSE for simplicity)

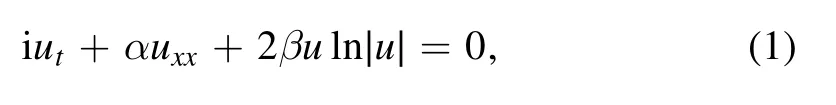
and obtained an analytic soliton-like solution namely Gausson for being of Gaussian wave shape.This is one of the most remarkable features of the LNSE.It also had been shown that the Gaussons can exist for any number of dimensions,and numerically are stable under collisions over a wide range of energies in one and two dimensional cases[4].Therefore,the model is applied to different areas such as superfluidity,open quantum systems,quantum liquid mixtures,Bose–Einstein condensates,and so forth [5–12].

On the other hand,some scholars studied real logarithmic nonlinear wave equations [13–19].For example,Carles and Pelinovsky studied log-KdV equation and the stability of its Gaussian solitary waves [15].Biswas et al solved the Bousisinesq equation with first degree logarithmic nonlinearity[17]; Darvishi and Najafi gave the Gaussian waves for some logarithmic ZK equation [18].In addition,Wazwaz et al studied several logarithmic nonlinear evolution equations and obtained Gaussian solitary waves solutions,such as the following log-KdV,log-KG,log-Boussinesq,log-BBM,log-BBM-KP,log-TRLW and so forth [20–23]:

It is obvious that the logarithmic nonlinear terms in the above equations are only the first degree form of ln∣u∣,and hence we can get the Gaussian solitary wave and the Gaussson by the elementary integral method.However,if we consider high order derivative dispersion,the shape of the Gaussian solitary wave and Gausson wave will not be kept.Therefore,if we hope there also exist the Gaussian solitary wave or the Gaussons for high dispersive wave motions,we have to consider more high degree nonlinear logarithmic terms likeln2∣u∣so that the balance between them can still keep.

It is well-known that to construct the soliton equations is a meaningful work in integrable systems.These soliton equations play an important role for recovering the mechanism of the existence of solitons.Similarly,in the paper,our aim is to try to find the mechanism of the existence of the Gaussian waves for high degree logarithmic nonlinear wave propagations.We propose two nonlinear wave equations with a second degree logarithmic nonlinearity,and show their Gaussian propagation patterns.Because of the existence of the second degree logarithmic nonlinearity,these equations cannot be solved by the routine direct integral method,and hence we use the trial equation method [24–27] to get their integrable factor equations and give the explicit constructions of the Gaussian waves.In fact we provide a new type of trail equation namely logarithmic trial equation which is different to the usual rational or algebraic trial equations to solve two models.Our results mean that the Gaussian solitary waves and the Gaussons can exist not only for the first degree logarithmic nonlinearity but also for the high degree logarithmic cases,and show that the key for the existence of the Gaussian waves is also due to the balance between the dispersion and logarithmic nonlinearity.

The paper is organized as follows.In section 2,we construct two second degree logarithmic nonlinear wave equations.In sections 3 and 4,we obtain the Gaussian wave solutions for two model equations.Last section is a short conclusion.

2.Model equations

For the usual wave equation

there are the traveling wave solutions with fixed velocity v= ±k,and there are no dispersion and dissipation.If we consider dispersive wave equation,such as

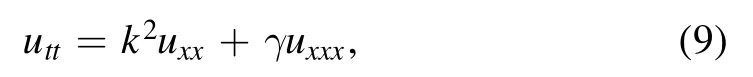
we will find its traveling wave solutions are the forms of hyperbolic functions or tangent functions which are not the Gaussian solitary wave.If we consider a nonlinear term(u2)xx,the Boussinesq equation

will be an integrable equation and hence there exist the soliton solutions like sech-function solution.However,it has no the Gaussian solitary wave solution.

On the other hand,by an elementary integral method,we can find there exists a Gaussian solitary wave solution for the following equations (22),(23)

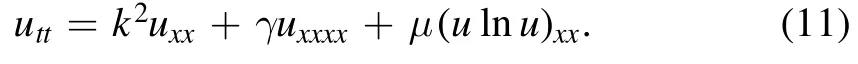
Furthermore,Wazwaz studied another wave equation

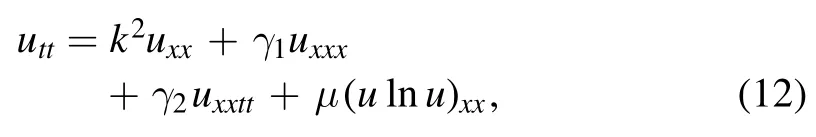
which is a kind of Boussinesq equation with dual dispersion and logarithmic nonlinearity.For this equation and other related logarithmic nonlinear wave equations,all their logarithmic terms are of the first degree on lnu .

If we consider high order dispersive effect,a natural problem is how to restrain dispersion so that the wave profile cannot be destroyed.We find that if a second degree nonlinear logarithmic term is considered,the balance between dispersion and nonlinearity will be achieved.Consequently,the second degree logarithmic nonlinear wave equation is given as follows

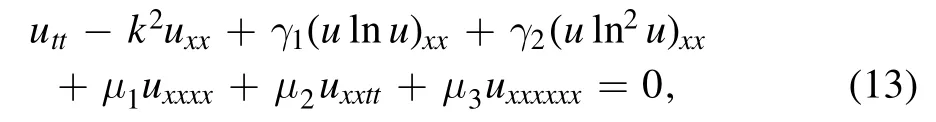
whereγ1,γ2,μ1,μ2,μ3are coefficients of logarithmic nonlinearities and dispersions and satisfyγ2μ3＜0.In addition,ln u can be written as ln∣u∣.If we only consider the Gaussian solitary wave,u will be positive,so we need not to write the absolute value symbol.

As the second model,we consider the high degree logarithmic version of equation (1).Indeed,for the first degree logarithmic nonlinear Schrödinger (1),as mentioned above,there exists a Gausson which is a localized nonspreadable solution,and keeps shape in propagation.This is just due to the balance between the logarithmic term and the second order derivative term.However,in general,Gausson will be destroyed if we consider only the high order dispersive terms or the high degree nonlinear logarithmic terms For the existence of Gaussons,we must keep the balance between dispersion and nonlinearity.And hence we propose the following nonlinear Schrödinger equation

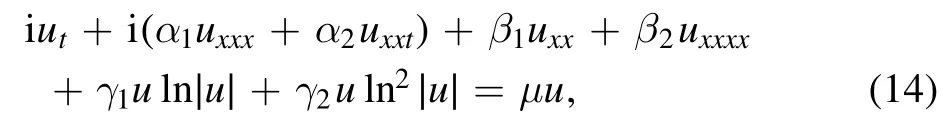
which includes high order dispersive terms and a second degree nonlinear logarithmic term,and where the right side is the detuning term,u is the wave profile,β2γ2＜0,all parameters are constants depending on the concrete model.When α1= α2= β2= γ2= 0,it becomes the equation (1).When γ1= γ2= 0,it describes the optical propagation in a linear dispersive media.We will prove that there exists the Gausson solutions for it.

The second degree logarithmic nonlinear terms ln2u in equations(13)and(14)show a high order effect of nonlinear interaction by which the balance between the highest order nonlinearity and the high order dispersions such as the sixth order derivative in equation (13) and the fourth order derivative in equation (14) can be kept so that the Gaussian solitary waves can be given.In some real models,the term ln2uwill appear naturally.For example,if we take the nonlinear interaction asus−1in the chain model of propagation of acoustic wave,then we expand it at s=1 to getus−1− 1= (s− 1) lnu+We will study it in details in further work.

Unlike the equations(1)–(7)can be solved by elementary integral method,these two model equations (13) and (14)cannot be reduced directly to the integral forms since they contain the high order derivative terms Thus,in next sections,we use the logarithmic trial equation method to solve them.

3.Gaussian wave solution for equation (13)

Firstly,Taking the traveling wave transformation

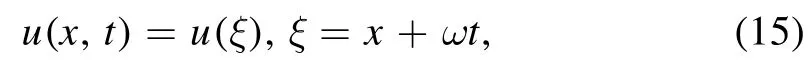
and substituting it into equation (13) and integrating twice yield the ODE as follows

where we have taken two integral constants to be zeros.

Then take trial equation

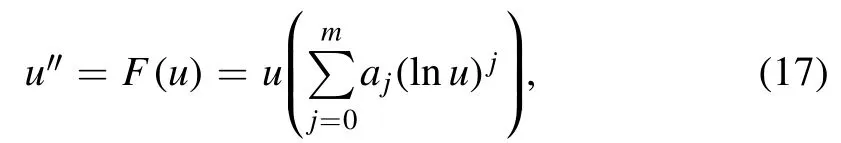
where m and ajare constants to be determined forj=0,… ,m.Setting it into equation (16),by the balance principle we get m=1.Therefore,the trial equation equation is given by

From the equation (18),we derive out by taking the integral constant be zero

and

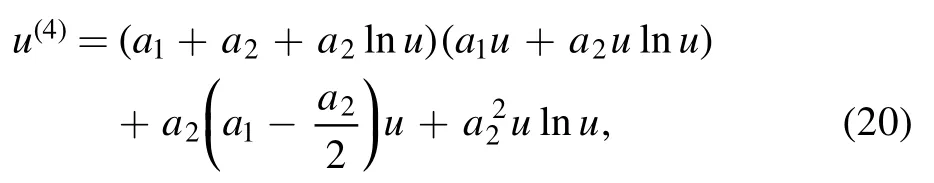
and substitute them into equation (16) to get an identity

Letting all coefficients be zeros yields a system of nonlinear algebraic equations

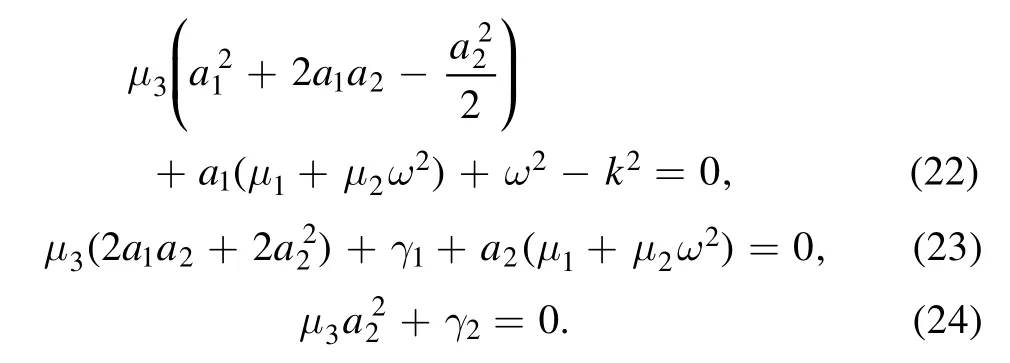
Solving the equations system,we get

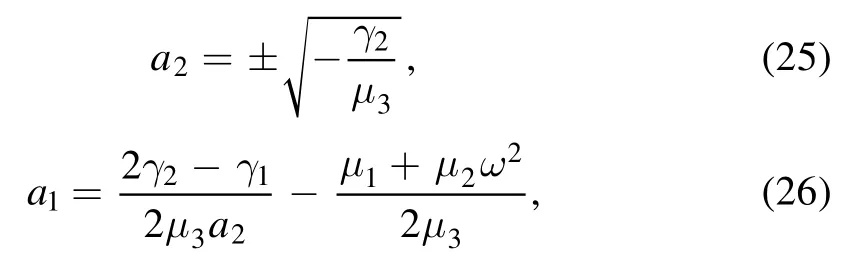
and the parameters condition

Therefore we can solve the equation (19),that is

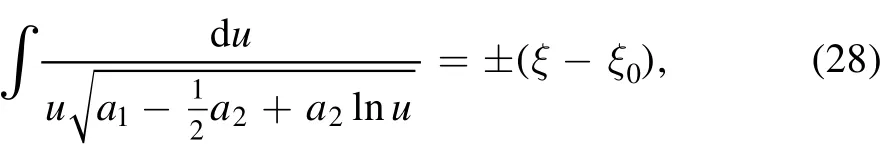
whereξ0is an arbitrary constant.And then we give the desired Gaussian solitary wave solution

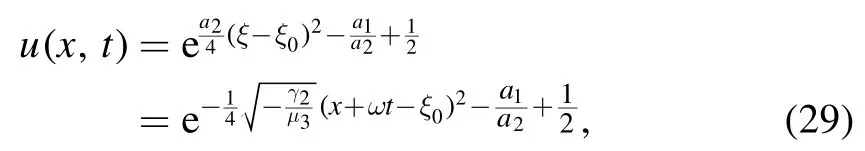
For concrete parameters,we can obtain concrete Gaussian solitary waves.For example,we takeγ1=2,γ2=1,μ1= 1,μ2= 1,μ3= − 1 ,k=ω= ±1,then we geta2= − 1,a1=1.So the Gaussian solitary wave is given as follows:

4.Gausson for equation (14)

Firstly,substituting envelope traveling wave transformation

into equation (14) and separating real and imaginary parts yield two ODEs as follows

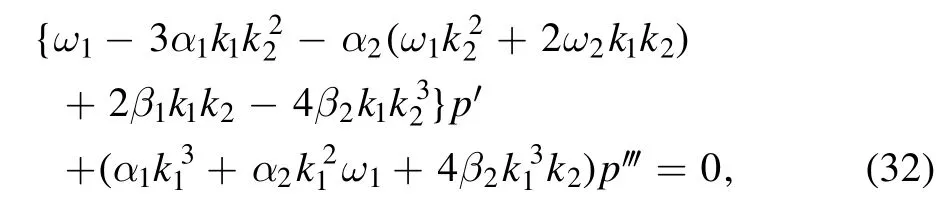
where

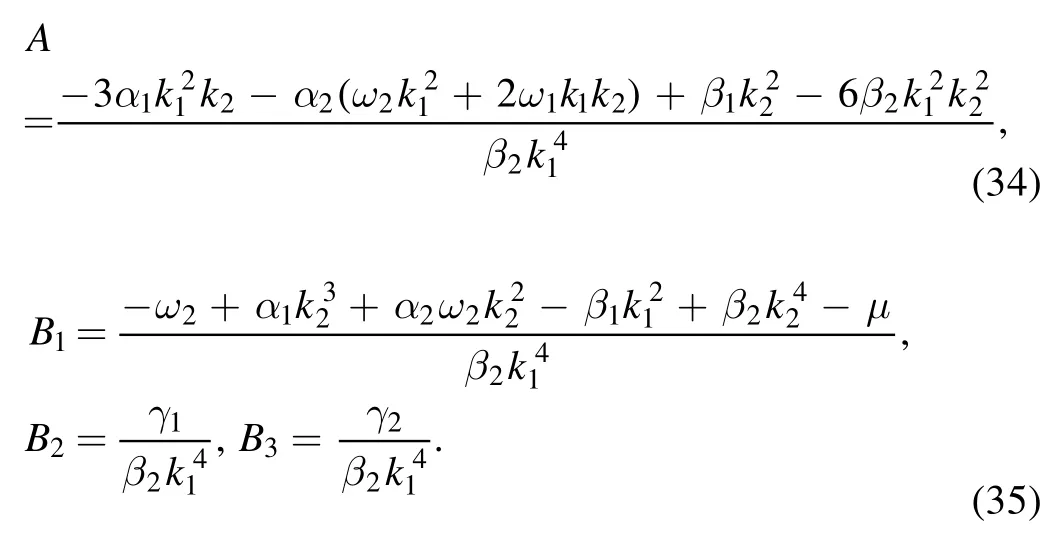
In equation(32),we let the coefficients ofp′andp′ be zeros to give

Solving the equations system,we get the parameters relations

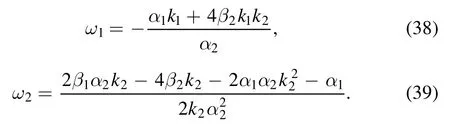
Under the above conditions,we only need to solve equation (33).Since equation (33) has the similar form with equation (16),we can solve it by the same method as above section.However,they have different parameters,for the purpose of completeness,we list the computations.

By the same way with the equation (13),the trial equation equation is given by

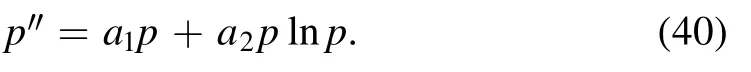
From the equation (40),we have by taking the integral constant be zero

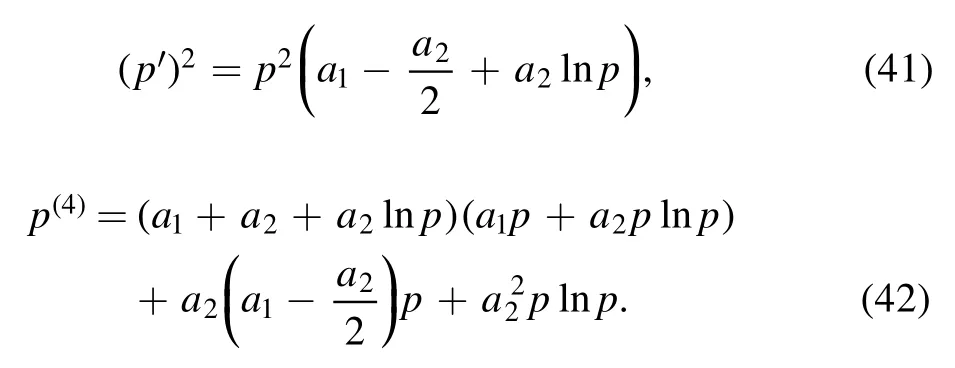
Furthermore,substituting them into equation (33) gives an identity

Letting all coefficients be zeros yields a system of nonlinear algebraic equations

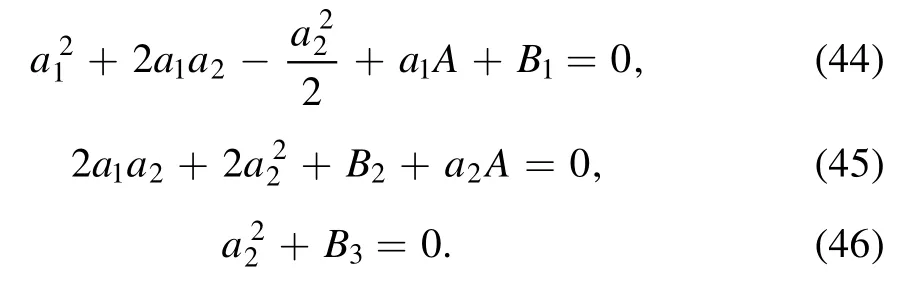
Solving the equations system,we get

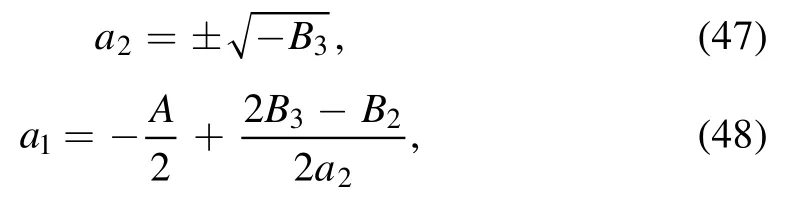
and all undetermined parametersk1,k2,ω1,ω2must satisfy the condition

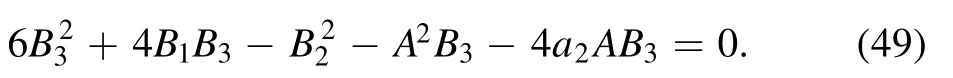
Next we write the equation (41) as the integral form

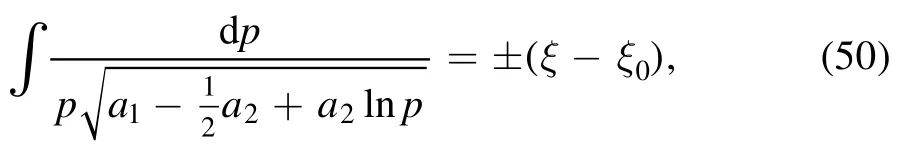
whereξ0is an arbitrary constant.And then solving the integral gives

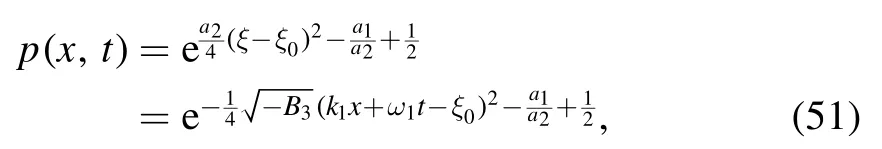
For concrete parameters,we can give concrete Gaussons.For example,we take1,γ2= − 1 ,k1= 1,ω2= −1,then we getSo the Gausson solution is given as follows:

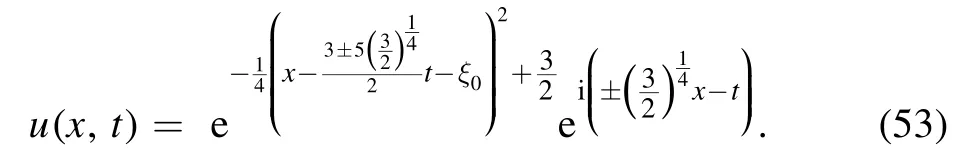
Remark 2.For the second degree logarithmic nonlinear Schrödinger equation(14),it is just the third and fourth order dispersions to balance the effect of second degree logarithmic nonlinearity.Here,the third order dispersion is a necessary term for p being dependent with temporal variable t.Indeed,if we remove this term,that is,if we takeα1=α2= 0,the model equation becomes

From equations(36)and(37),we must haveω1= 0.Without loss of generality,we can takek1=1andk2=0.The degenerate Gausson is given by

It is easy to see that the amplitude of the wave is of Gaussian shape and is independent with the temporal variable,while the phase of the wave is independent with the spatial variable.

5.Conclusion

Due to the balance between dispersion and logarithmic nonlinearity,the Gaussian waves can exist for two second degree logarithmic nonlinear model equations.These equations include both real and complex cases.In addition,for all model equations (2)–(7) in introduction,we can give the second degree logarithmic forms For example,

The above these high degree logarithmic nonlinear equations show the balance between logarithmic nonlinear and dispersion,and hence can be solved by the trial equation method,and hence the Gaussian waves can be given.This should be a basic principle for the existences of Gaussian solitary waves or Gaussons for the propagation patterns in high degree nonlinear logarithmic media.