Magnetohydrodynamic flow and heat transfer of a hybrid nanofluid over a rotating disk by considering Arrhenius energy

M Gnaneswara Reddy,Naveen Kumar R,B C Prasannakumara,N G Rudraswamy and K Ganesh Kumar

1 Department of Mathematics,Acharya Nagarjuna University Campus,Ongole—523 001,India

2 Department of Studies and Research in Mathematics,Davangere University,Shivagangothri,Davangere-577007,Karnataka,India

3 Department of Mathematics,P.C.Jabin Science Collage,Hubballi-580031,India

Abstract This research work explores the effect of hybrid nanoparticles on the flow over a rotating disk by using an activation energy model.Here,we considered molybdenum disulfide and ferro sulfate as nanoparticles suspended in base fluid water.The magnetic field is pragmatic normal to the hybrid nanofluid flow direction.The derived nonlinear ordinary differential equations are nondimensionalized and worked out numerically with the help of Maple software by the RKF-45 method.The scientific results for a non-dimensionalized equation are presented for both nanoparticle and hybrid nanoparticle case.Accoutrements of various predominant restrictions on flow and thermal fields are scanned.Computation estimation for friction factor,local Nusselt number and Sherwood number are also executed.Results reveal that the reduction of the heat transfer rate is greater in hybrid nanoparticles when compared to nanoparticles for increasing values of Eckert Number and the thermal field enhances for the enhanced values of volume fraction.

Keywords: porous medium,MHD,hybrid nanoparticles,activation energy

Nomenclature

Greek symbols

Subscript

1.Introduction

In the year 1889,Sweden’s Nobel laureate Arrhenius embarked upon a theory encompassing the reaction rate of numerous chemical processes.The theory averred the relationship between temperature and reaction rate in an equation form termed the Arrhenius equation.He stated that the minimum energy required to begin a chemical reaction is called the activation energy.Later,the term was coined as Arrhenius activation energy.Furthermore,the nature of Arrhenius activation energy was re-examined by Menzinger and Wolfgang [1].Jensen [2] scrutinized the contemporary use of the Arrhenius equation and activation energy through ICs.Hayat et al [3] addressed the influence of activation energy in the flow of dyadic chemically reactive third-grade fluid through a rotating disk.Khan et al [4] exhibited the influence of dyadic chemical reaction and Arrhenius activation energy with second-law scrutiny on nanofluid flow.Salahuddin et al [5] examined the inner energy change and stable-state 3D change in visco-elastic fluid flow in revolving state with added convective boundary conditions.The impact of Arrhenius activation energy on tangent hyperbolic fluid flow above an impelling stretched surface with zero mass-flux conditions was revealed by Kumar et al [6].Khan et al [7]calculated the effect of Arrhenius activation energy on chemically reactive rotating flow subject to heat source and nonlinear heat flux.Asma et al[8]numerically examined the magnetohydrodynamic (MHD) flow of nanofluid due to a rotating disk with the effect of activation energy and chemical reaction.

MHD flow has a wide range of applications in engineering,geophysics,astrophysics,the study of earthquakes,aerospace engineering and biological fields.Ramzan et al[9]used Eyring–Powell nanofluid to illustrate MHD flow,taking account of chemical reactions.Zeeshan et al [10] scrutinized the MHD Couette–Poiseuille nanofluid flow by considering activation energy along with the chemical reaction.Stagnation-point flow and the effect of Newtonian heating over the surface of a nanofluid were investigated by Hakeem et al[11].Lu et al [12] scrutinized the MHD flow with the help of Carreau nanofluid by applying zero mass-flux condition.Khan et al [13] considered 3D flow over a two-directional stretching sheet by using the Carreau rheological model.In researching magnetic effect,heat generation/absorption is taken into the account.The outcome of the research revealed that the velocity is dependent on Hartmann number.Reddy and Sandeep [14] explained the phenomena of MHD flow of Carreau nanofluid through the analysis of the different effects.

The fluid flow over a surface of rotating disks has attracted tremendous interest from scientists due to its several technical and aerospace applications.Greater effort from researchers is required in order to discover the hidden properties of rotating disks.This is because the fluid flow conduction through rotating disks is not only of speculative interest,but has practical significance in the use of medical equipment,gas turbines,chemical processes and rotating machines.Therefore,research into liquid flow over an infinite disk with rotation was first initiated by Karmann [15].Turkyilmazoglu [16] investigated the well-known Karmann viscous pump problem over a stretchable disk with rotation.The flow of nanofluid through a rotating disk was scrutinized by Turkyilmazoglu[17].Hayat et al[18]investigated the Jeffrey nanofluid flow with convection between two rotating stretchable disks.The heat variation of nanofluid flow through a rotating disk with a consistent escalation rate and three different nanoparticles was appraised by Yin et al [19].The quantitative simulation of radiative flow with carbon nanotubes and partial slip of nanofluid was done by Hayat et al[20].Rehman et al [21] gave the numerical solution of non-Newtonian fluid flow over a rigid inflexible rotating disk.Rafiq and Mustafa [22] analyzed the swirling unsteady nanofluid flow around a decelerating porous rotating disk.Turkyilmazoglu [23] proposed the idea of the interaction of fluid flow with suspended particles over a stretching rotating disk.Tassaddiq et al [24] probed the incompressible hybrid nanofluid flow in the presence of a magnetic field over an infinite impervious rotating disk.

Nanofluid flow has attracted the attention of engineers and scientists over the past two decades.Nanofluid is an innovative engineering material that has numerous applications in biology,cancer diagnosis,nuclear industries,drilling and oil recovery,electronic cooling,heat exchangers,cooling of microelectronics,vehicle cooling and vehicle heat management.To improve the thermal conductivity of nanofluids and evaluate the properties of heat transfer,hybrid nanofluids were introduced.A mixture of dual diverse nanoparticles yields hybrid nanofluids.Recently,several researchers scrutinized the mono and hybrid nanofluid flow over different surfaces.Ramesh et al [25] studied the influence of thermal radiation on MHD stagnation-point flow of nanofluid over a stretching surface with variable thickness.Sheikholeslami et al [26] scrutinized the impact of thermal radiation on natural convection ofFe3O4-ethylene glycol nanofluid,taking account of the electric field in a porous enclosure.Kumar et al scrutinized[27]the impact of Joule and viscous dissipation on 3D flow of nanoliquid in slip flow regime under timedependent rotational oscillations.Sharma et al [28] investigated the flow of nanofluids driven by the mutual effects of peristaltic pumping and external electric field past a microchannel,taking account of double-diffusive convection.Prakash et al[29]gave the mathematical modeling of electroosmotic flow of non-Newtonian nanofluids through a microchannel in the presence of Joule heating and peristalsis.Ramesh et al[30]scrutinized the flow of hybrid nanomaterial subjected to the convergent/divergent channel.Several researchers studied the nanofluid flow over different surfaces,taking account of the Joule effect,viscous dissipation and other influencing factors [31–35].

Inspired by all the above studies,the present work elucidates the activation energy flow associated with different nanoparticles,which was not considered in previous works.Hence,the earnest attempt made to probe the thermo-physical properties of nanofluid on MHD flow with the rotating disk.The present research problem is solved numerically.The results obtained are presented graphically and discussed briefly.

2.Mathematical formulation

Consider the 3D steady flow of incompressible hybrid nanofluid suspended with different kinds of nanoparticles over an infinite stretching rotating disk,under the influence of a magnetic field.The disk rotates about the z-axis with an angular velocity Ω.The heat transfer process is examined subject to dissipation and Joule heating.Geometrical representation of the considered flow problem is depicted in figure 1.In addition,we have considered the impact of the activation energy and binary chemical reaction aspects in analyzing the mass transfer.

The modeled governing equations are as follows:

with boundary conditions,

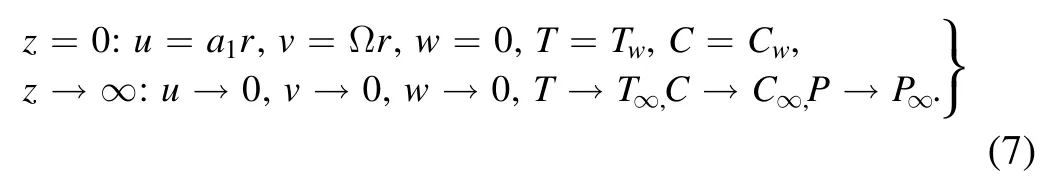
Here,(u,v,w) are the velocity components T,Tw,T∞,the temperature of the fluid,wall temperature and ambient temperature,respectively.

We consider the transformations:

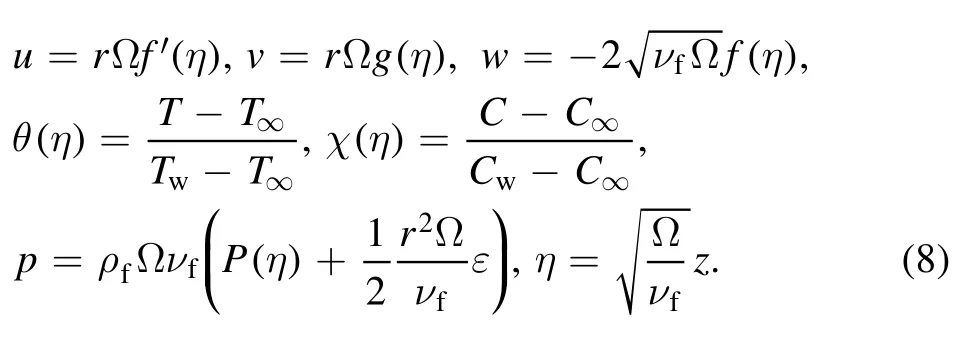
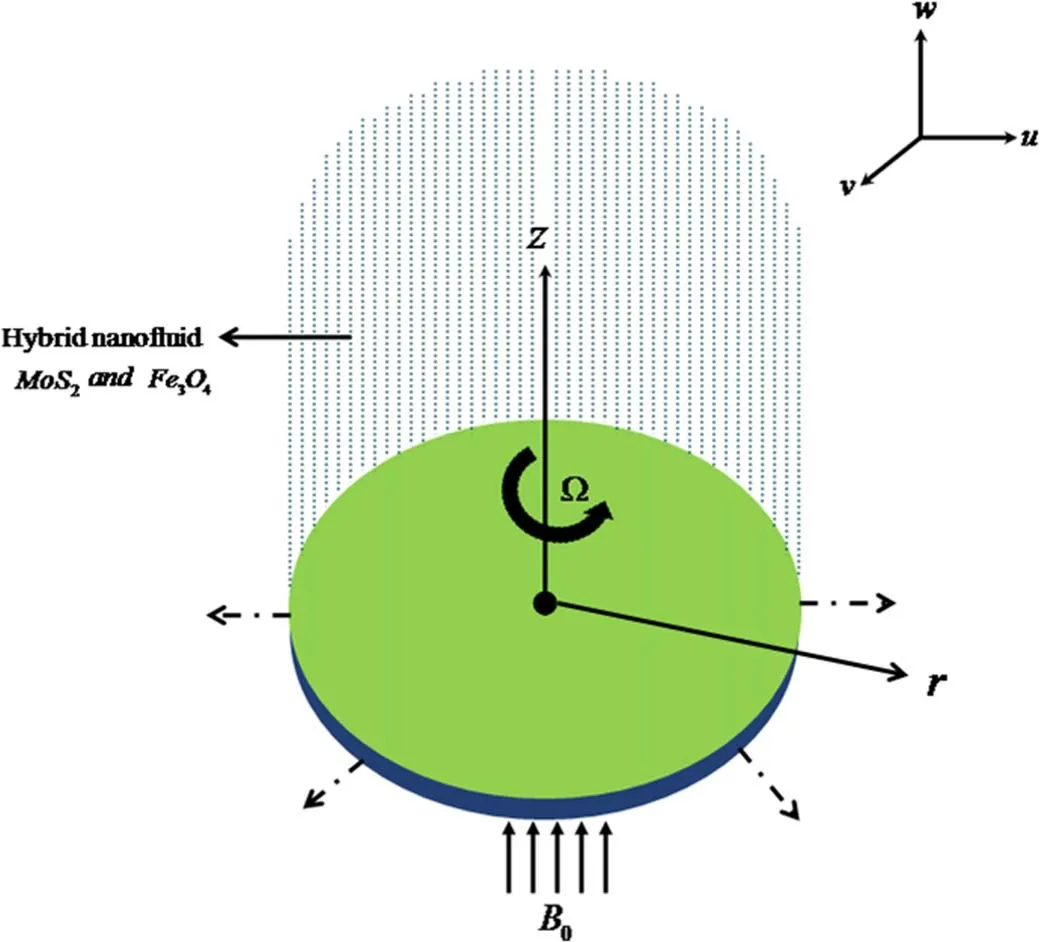
Figure 1.Flow configuration.

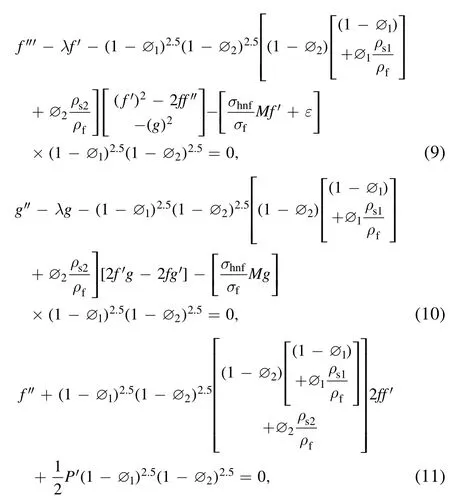
In view of equation (8),the continuity equation is satisfied exactly and equations (2)–(7) reduced as below:

Similarly,the transformed boundary conditions are:

where

Table 1.Thermo-physical properties of nanoparticles.

Here,σ-reaction rate,E-activation energy,δ-temperature difference andλ,Sc,M,Ec,Pr,Re,Aare the porosity parameter,Schmidt number,Hartmann number,Eckert number,Prandtl number,local Reynolds number and stretching parameter,respectively.

Equation(9)is differentiated with respect toηas follows:

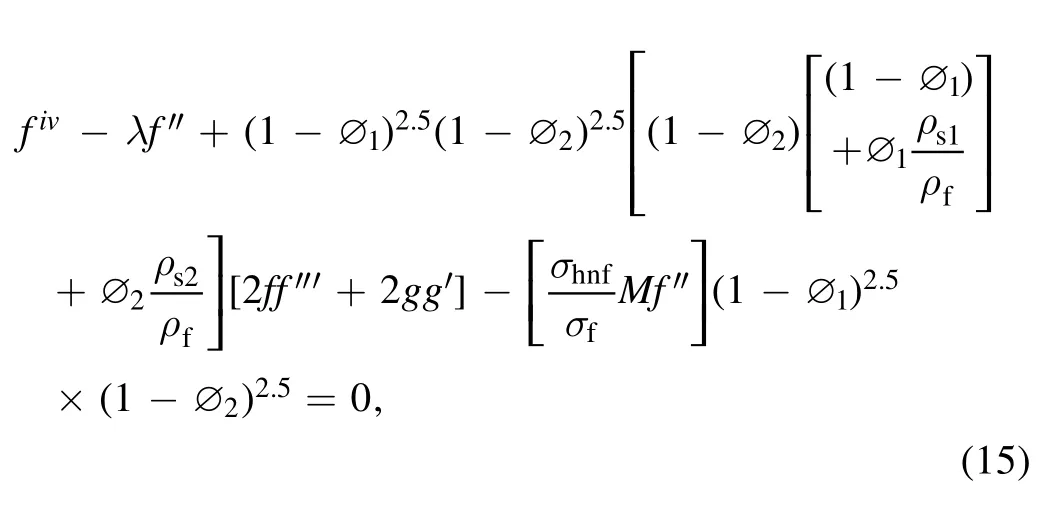
where,(ρhnf,μhnf,khnfand(ρCp)hnf) are given below:

TheSh,NuandCfare given as:

The non-dimensional form ofRe−1/2Sh,Re−1/2NuandRe1/2Cfxare:

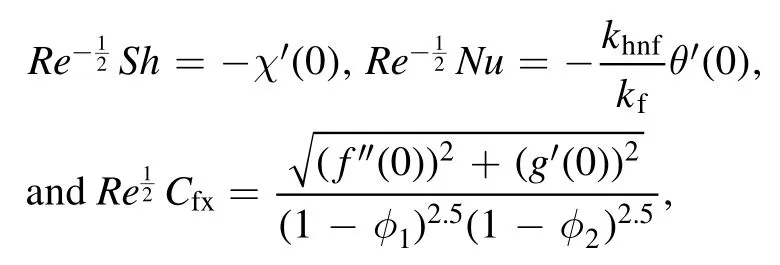
3.Result and discussion

This section covers the outcomes of the MHD flow over a rotating disk with suspension of different nanoparticles.Two types of oxides,namely molybdenum disulfide and ferro sulfate,are suspended in base fluid water.The powerful numerical mechanism RKF fourth-fifth order along with a shooting technique is used to deal the non-dimensional governing equations of the present problem.Table 1 presents the thermo-physical properties of each base fluid and the nanoparticles.In order to provide insight,the effects of various governing parameters on thef′(η),g(η),θ(η) andχ(η) are discussed graphically.

Figures 2–4 show the domination ofMoverf′(η),g(η),andθ(η) for the cases of hybrid nanoparticles and nanoparticles.Here,an escalating integrity ofMdecays thef′(η),andg(η) (see figures 2 and 3).Likewise,the thickness of the corresponding layer reduces for enhanced values ofM.In addition,the velocity of the fluid is lower in nanofluid when treated with hybrid nanofluid.Substantially larger values ofMincreased the Lorenz force.Consequently,the accelerated Lorentz force generates extra drag to the ambulation of the fluid flow and nanoparticles.From figure 4 it can be seen thatθ(η) results in larger integrities ofM.Furthermore,the corresponding thermal field increases for largerM.The impact ofλonf′(η) ,andg(η)is shown in figures 5,6.Here,it is contemplated that the escalating values ofλdecrease both the profilesf′(η) ,andg(η) of both the nanoparticle and hybrid nanoparticle case.Besides the interrelated thickness of the layer scales back for largerλ.In addition,the velocity of the fluid is lower in nanoparticles when treated with hybrid nanoparticles.

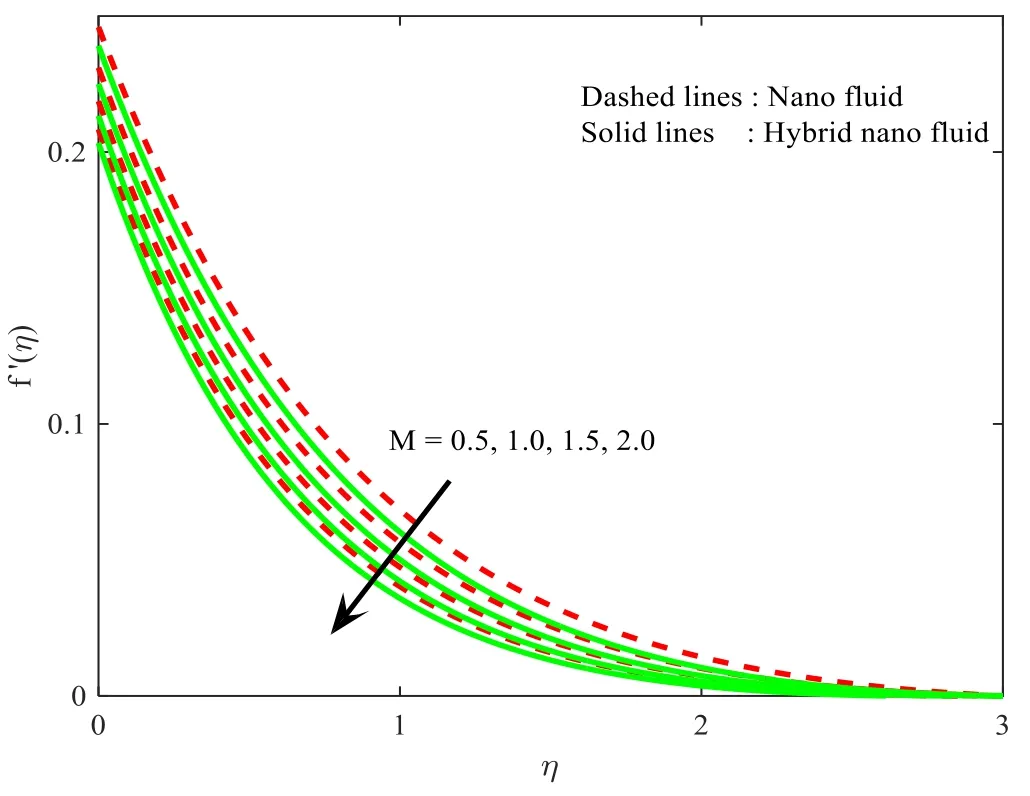
Figure 2.Influence of M onf′(η).

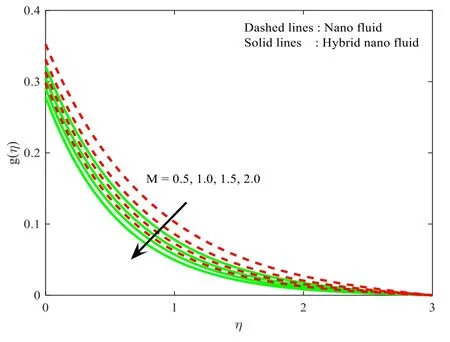
Figure 3.Influence of M on gη ().

Figure 4.Influence of M onθ (η).

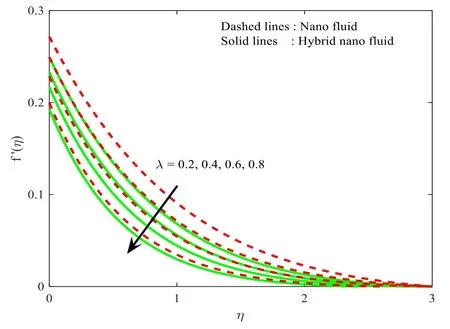
Figure 5.Influence ofλ onf′(η).

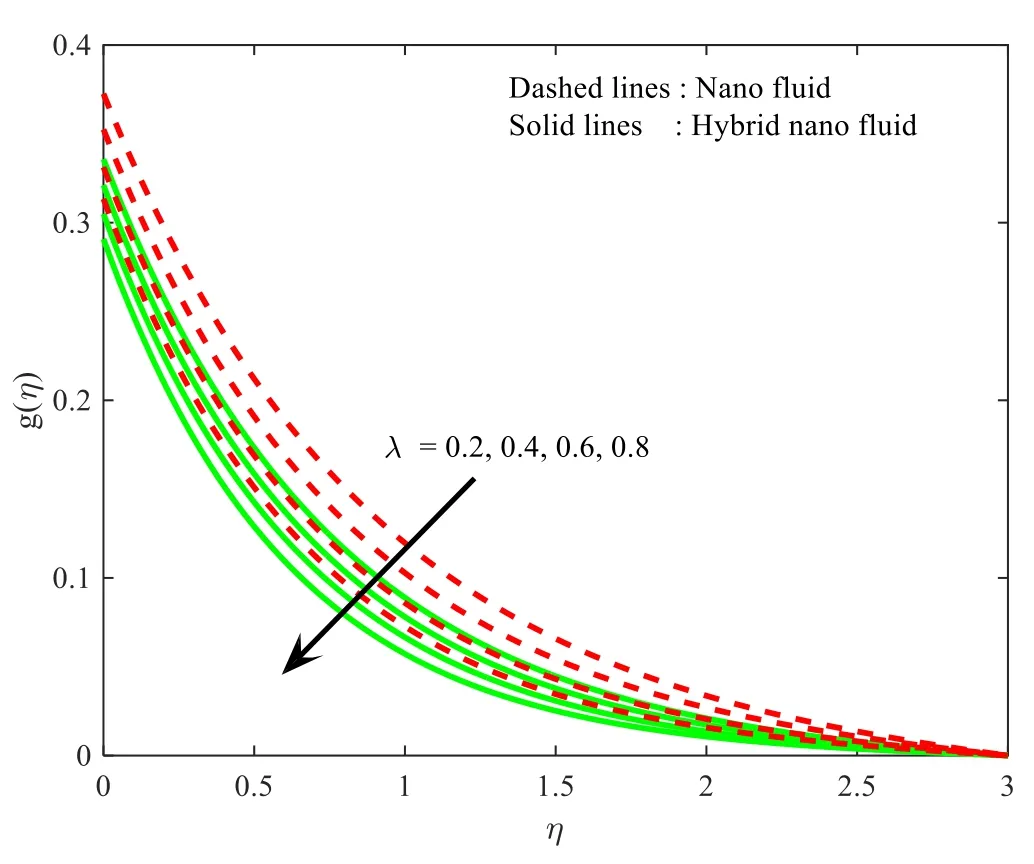
Figure 6.Influence ofλ on gη ().

The influence of ∅1onf′(η),andθ(η) profiles for both MoS2−H2O andFe3O4−H2O nanoparticle cases are depicted in figures 7,8.Here,it is noted enlarged values of volume fraction declines the velocity profile,but enhances the thermal profile.Furthermore,the compactness of the corresponding layers also provides for growing values ofK.Furthermore,the enhancement of fluid flow is higher in nanoparticles than that of hybrid nanoparticles.Figures 9,10 reproducef′(η),andθ(η)of both the hybrid nanoparticle and nanoparticle case for different values of ∅2.One may observe from these figure that the velocity profile is declined and thermal profile is enhanced for increased integrates of volume fraction ∅2.The compactness of momentum of both hybrid nanoparticle and nanoparticle cases declines for increasing values of ∅2parameter,but the opposite trend can be seen for thermal profile.

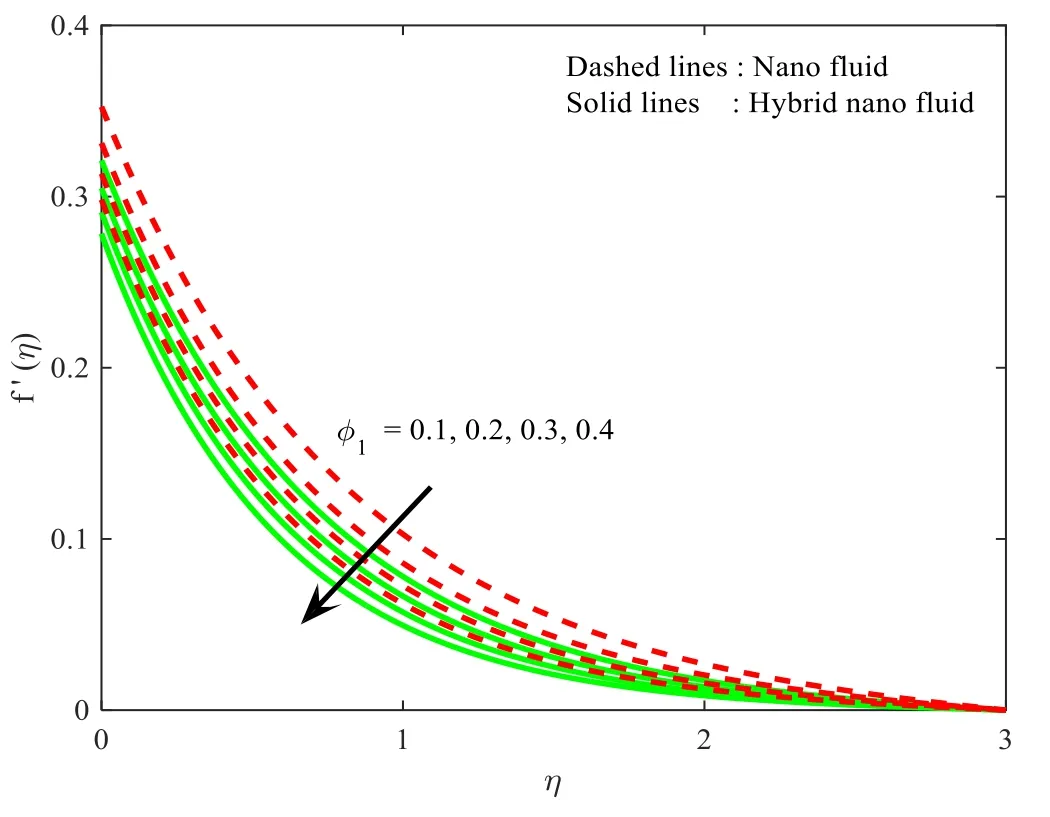
Figure 7.Influence of ∅1 onf′(η).

Figure 8.Influence of ∅1 onθ (η).

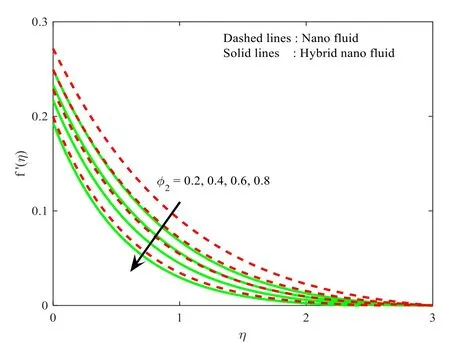
Figure 9.Influence of ∅2 onf′(η).

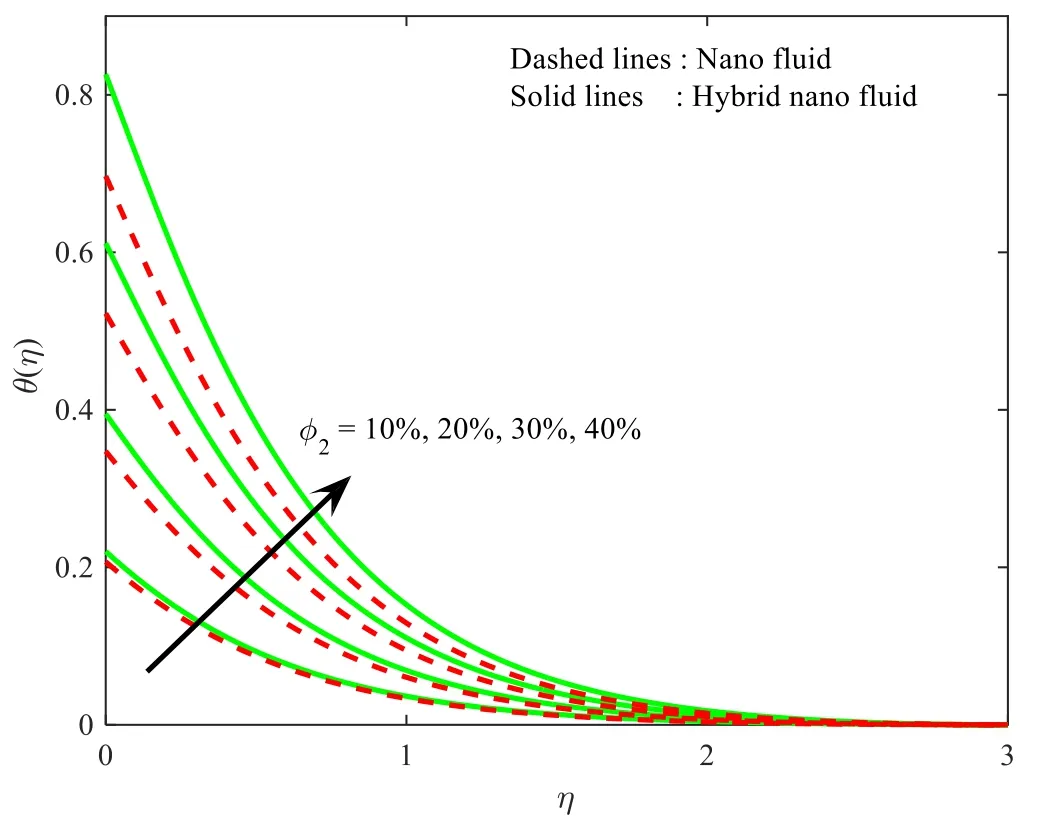
Figure 10.Influence of ∅2 onθ (η).

Figure 11.Influence ofEc onθ (η).

The influence of Eckert number on the thermal field of the nanofluid and hybrid nanofluid is displayed in figure 11.The increasing Eckert number increases the thermal field.In the case of a large magnetic force system,the major disruption of the temperature field induced by each member is an interesting result.These physical phenomena are attributable to the cumulative effect of heat energy stored in the nanofluid and hybrid nanofluid due to fractional heating.The variation in thermal field of the nanofluid and hybrid nanofluid versus Prandtl numberPris shown in figure 12.The graph shows that the thermal field and thermal layer thickness decline whenever thePrvalues are boosted.This is really caused by the fact that with the greater Prandtl number,fluids will have a comparatively low conductivity,which mostly diminishes the heat transfer and thickness of the thermal fluid flow and therefore the temperature of the fluid reduces.The effect ofPr on Newtonian fluids is close to what we are seeing in nanofluid.These characteristics are thus already retained by nanofluids.

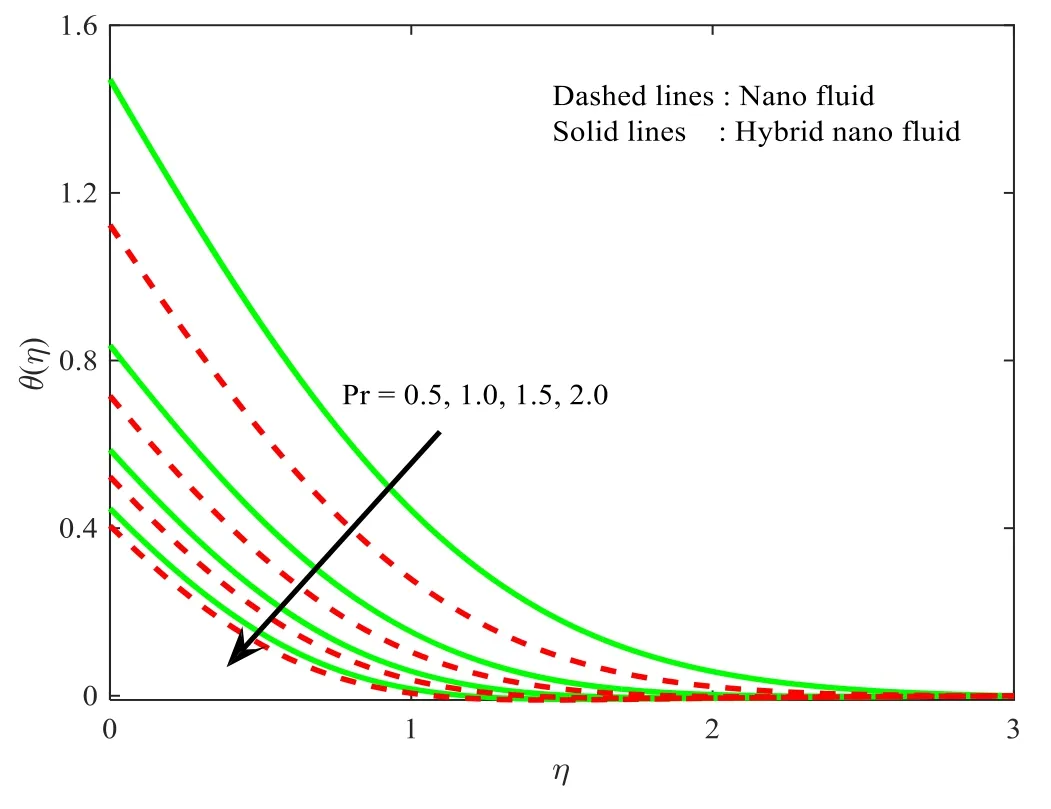
Figure 12.Influence of Pr onθ (η).

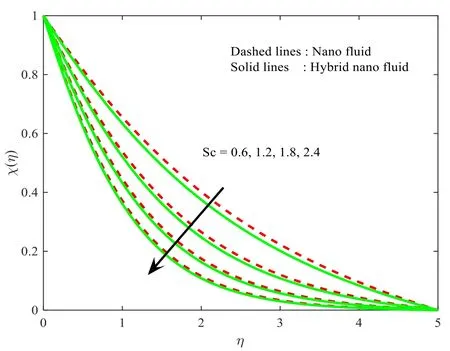
Figure 13.Influence ofSc onχ (η).

Figure 13 shows the denouement of theScparameter on theχ(η) profile for both the nanoparticle and hybrid nanoparticle case.Here,it is essential to mention that the extreme values ofScscale back the fluid concentration.Furthermore,the solutal layer of both the nanoparticle and hybrid nanoparticle case reduces for higher values ofSc.The influence ofσon the solutal field of the nanofluid and hybrid nanofluid is shown in figure 14.One may observe that the solutal field is scaled back for increment values ofσ.The compactness of the solutal layer of both the hybrid nanoparticle and nanoparticle case reduces for increasing values of the material parameter.In addition,the concentration of the fluid is much faster in the nanoparticle case when compared with the hybrid nanoparticle case.TheσandEonχ(η) for both the hybrid nanoparticle and nanoparticle case are depicted in figures 15,16.Here,it is observed that an increasing value ofEscales back the concentration of the fluid flow in both nanoparticle cases.

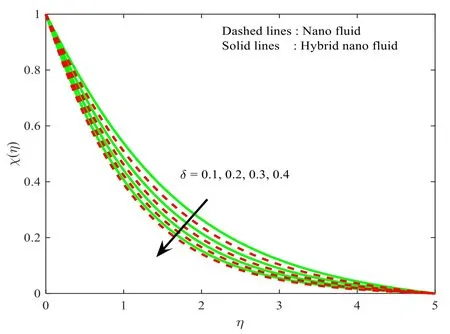
Figure 14.Influence ofδ onχ (η).

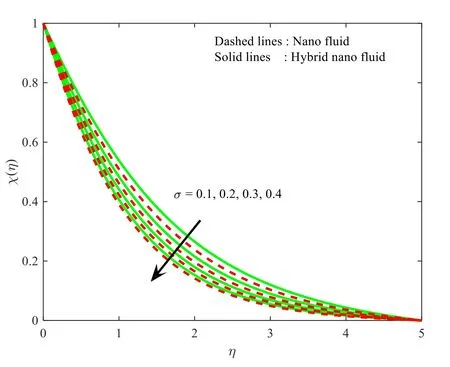
Figure 15.Influence ofσ onχ (η).

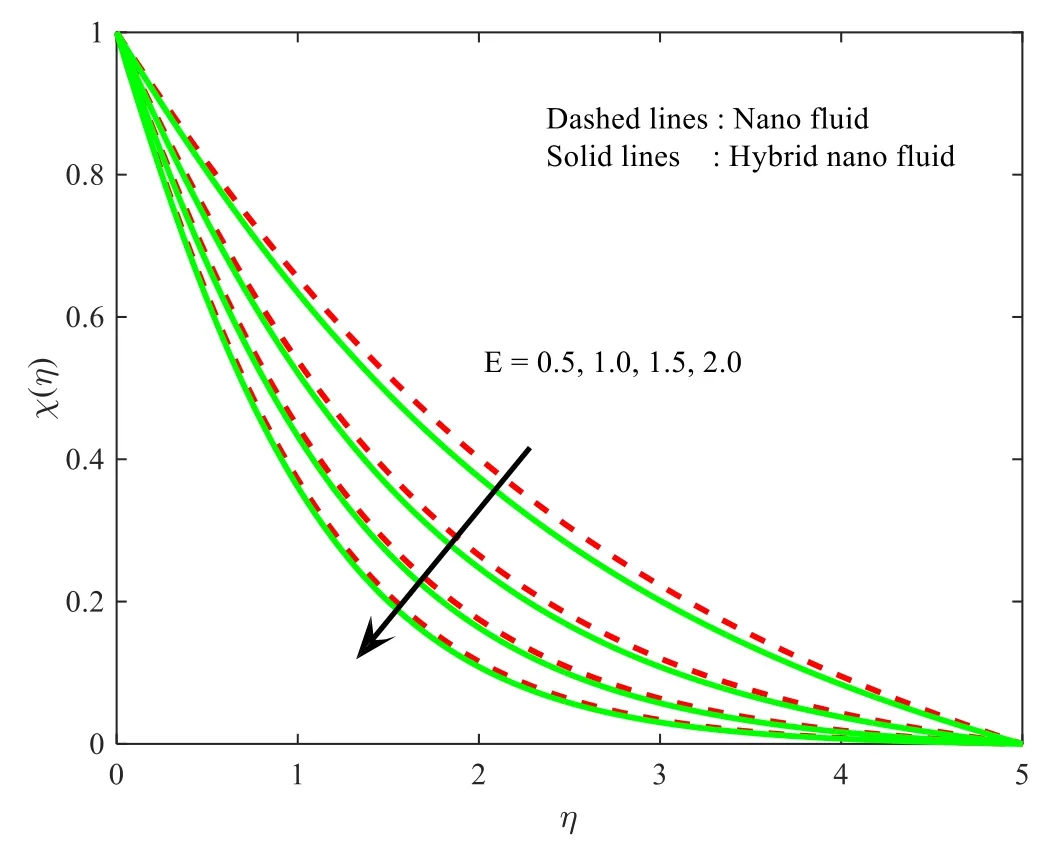
Figure 16.Influence of E onχ (η).

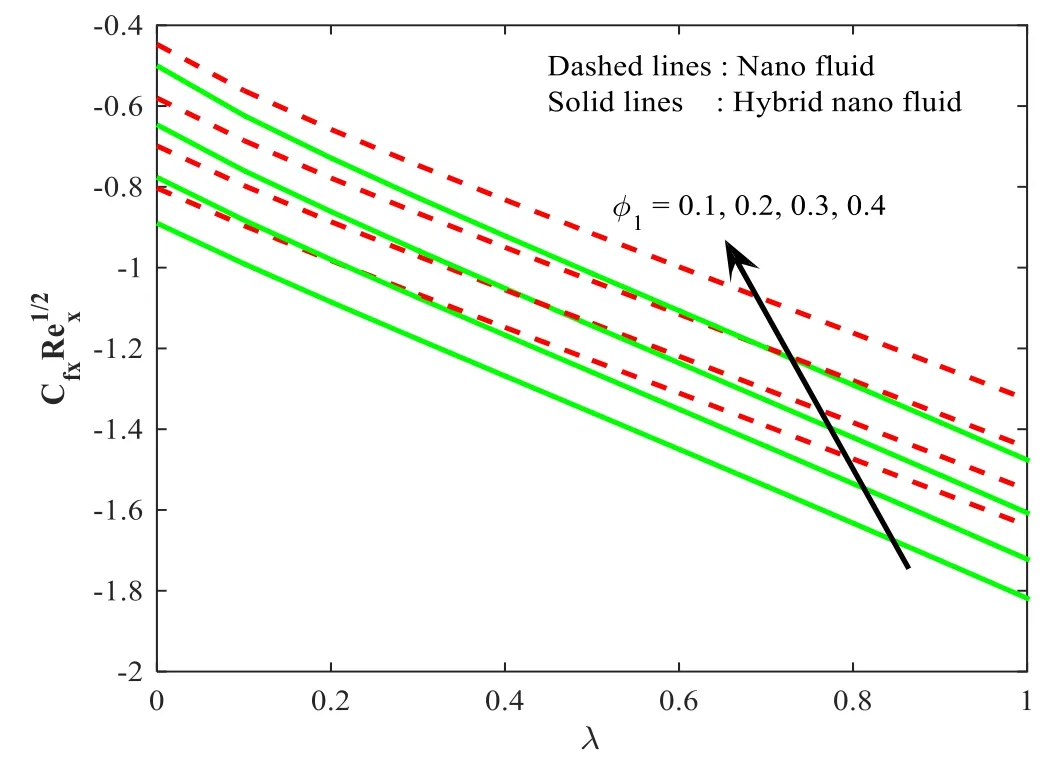
Figure 17.Influence ofλ versus ∅1 on Cfx.

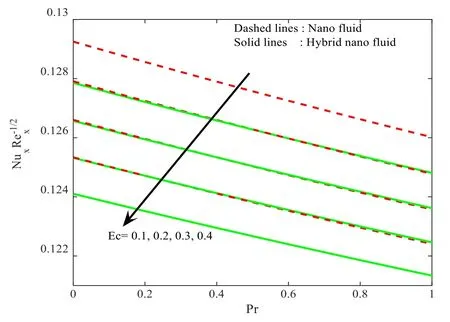
Figure 18.Influence of Ec and Pr on Re−1/2Nu.

The impact ofλand ∅1onRe1/2Cfxis delineated in figure 17.Here,it is contemplated that the escalating values ofλand ∅1scale back the friction factor for both the hybrid nanoparticle and nanoparticle case.Besides,there is an interrelated thickness of the layer downturn for largerλand∅.1Furthermore,the reduction of the friction factor is less in hybrid nanoparticles when compared to nanoparticles.Figure 18 represents the encounter ofEcandPronRe−1/2Nufor both the hybrid nanoparticle and nanoparticle case.One may observe that boosted values ofPr reduce the temperature of the fluid for both the hybrid nanoparticle and nanoparticle case.Hence,Re−1/2Nuis scaled back,while the opposite trend is observed for higher values ofEc.Figure 19 reproduces theRe−1/2Shfor varyingScandδfor both the hybrid nanoparticle and nanoparticle case.Here,it is essential to mention that larger values ofEcenhance theRe−1/2Shin both the hybrid nanoparticle and nanoparticle case.

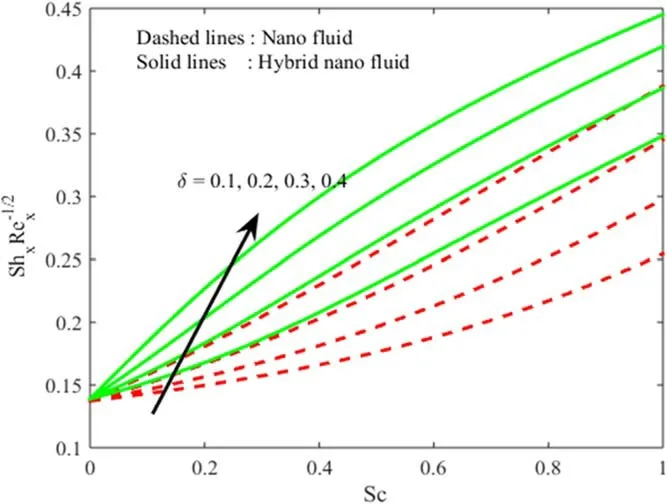
Figure 19.Influence ofδ andSc on Re−1/2Sh.

Table 2.Numerical values of Cfx for different physical parameter values.

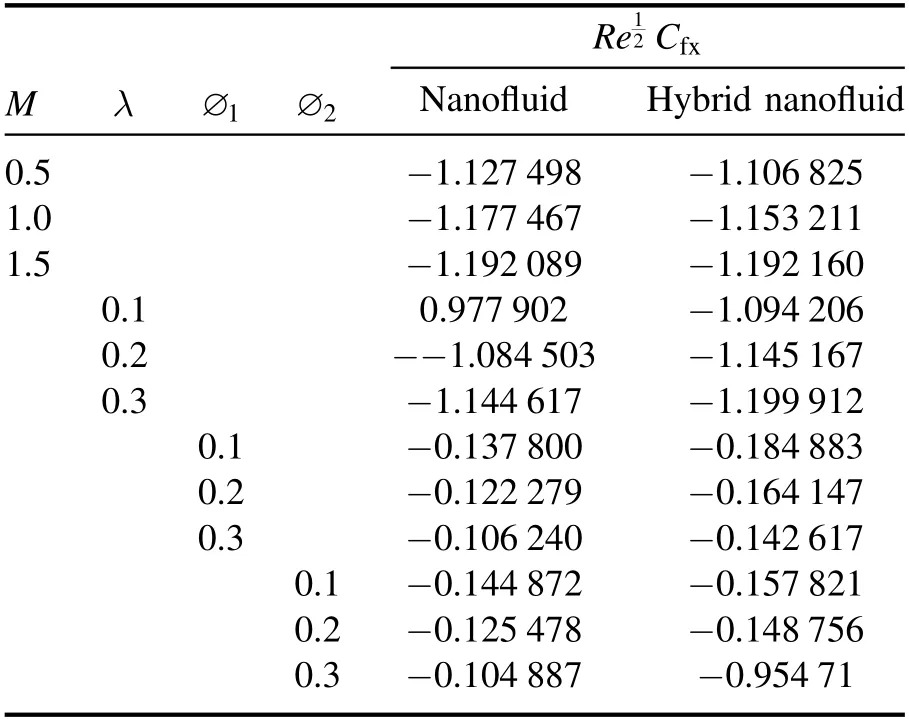
Table 2.Numerical values of Cfx for different physical parameter values.

Re Cfx 12 M λ ∅1 ∅2 Nanofluid Hybrid nanofluid 0.5 −1.127 498 −1.106 825 1.0 −1.177 467 −1.153 211 1.5 −1.192 089 −1.192 160 0.1 0.977 902 −1.094 206 0.2 −−1.084 503 −1.145 167 0.3 −1.144 617 −1.199 912 0.1 −0.137 800 −0.184 883 0.2 −0.122 279 −0.164 147 0.3 −0.106 240 −0.142 617 0.1 −0.144 872 −0.157 821 0.2 −0.125 478 −0.148 756 0.3 −0.104 887 −0.954 71

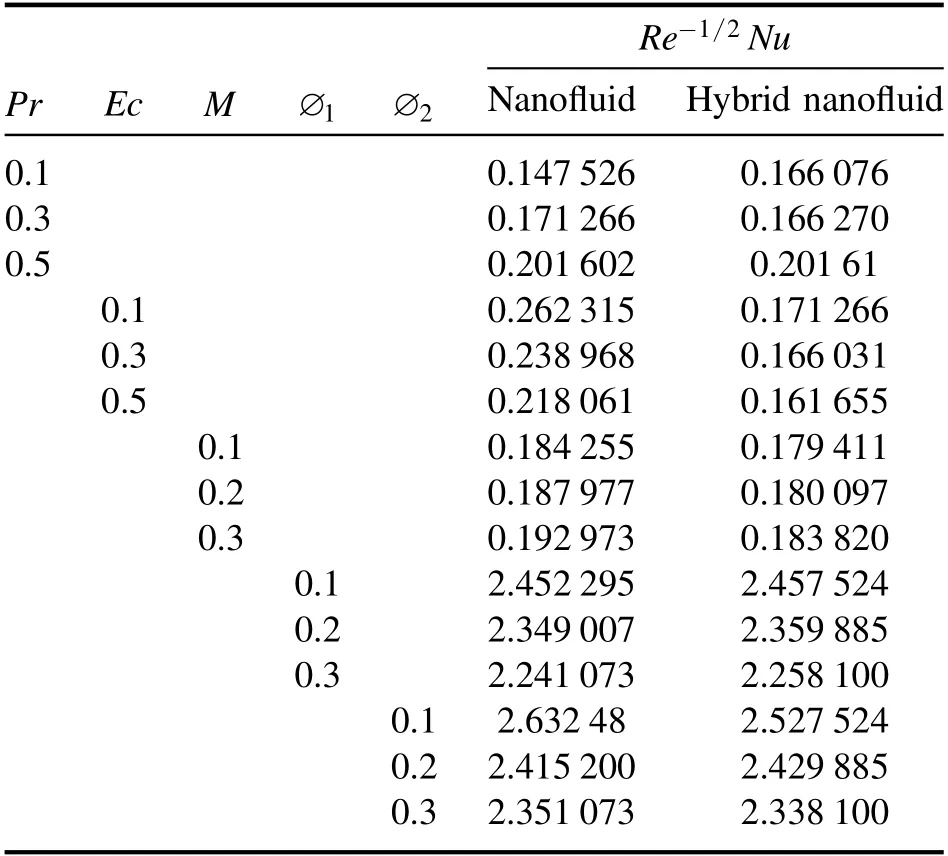
Table 3.Numerical values of Re−1/2Nufor different physical parameter values for both the hybrid and nanofluid case.

Table 4.Numerical values of Re−1/2Shfor different physical parameter values for both the hybrid and nanofluid case.

Table 5.Comparison of of statistical values with Miklavcic and Wang[36]in the absence of M,ε,λ Pressure gradient,nanoparticles,energy and mass effects.

The effects of diversified governing flow parameters on the friction coefficientsRe1/2Cfx,Re−1/2NuandRe−1/2Share listed in tables 2–4.From table 2,it can be seen that the fiction coefficient is enhanced by increasingMandλ,but a reverse trend is observed for both ∅1and ∅2.Furthermore,from table 2 it is noted that the value of the heat transfer rate scale back can be established by accumulating values of Pr,∅1and ∅2.While,a reverse trend is observed for booster values of bothMandEc.From table 4 it can be seen that the rate of mass transfer declined for increasing values ofScandσ.Table 5 gives the comparison of statistical values of the current problem with published results and it shows good agreement.

4.Conclusion

A hybrid nanoparticle performance of Arrhenius activation energy over a rotating disk by considering MHD is examined numerically.A powerful numerical mechanism RKF fourth and fifth order by adopting a shooting approach is used to deal with the non-dimensional governing equations of the present problem.The outcome of the velocity,concentration and temperature profile of both nanoparticle cases for distinct values of non-dimensional parameter are presented graphically and analyzed.Based on these graphs and tables we conclude that:

• enhanced values ofλdecrease the velocity profile for both cases

• enhancement of heat transfer is greater in hybrid nanoparticles when compared to nanoparticles for different values ofM

•f′(η)andg(η)is decreased for enhancing values of both∅1and ∅2

• largerσandScreduces the solutal boundary layer

• larger-scaleMandλslows down the fluid velocity of both nanoparticle cases

• thermal field enhances for increasing values of both∅1and ∅2.

Future work may add further value to the present topic by the investigation of hybrid nanofluid flow through new physical mechanisms,relevant influencing factors and a combination of different nanoparticles suspended in diverse carrier liquids.

Acknowledgments

The authors gratefully acknowledge the financial support from Dr D S Kothari Post-Doctoral Fellowship Scheme,University Grants Commission,New Delhi.