Perturbation,symmetry analysis,Bäcklund and reciprocal transformation for the extended Boussinesq equation in fluid mechanics
Gangwei Wangand Abdul-Majid Wazwaz
1 School of Mathematics and Statistics,Hebei University of Economics and Business,Shijiazhuang,050061,China
2 Department of Mathematics,Saint Xavier University,Chicago,IL 60655,United States of America
Abstract In this work,we study a generalized double dispersion Boussinesq equation that plays a significant role in fluid mechanics,scientific fields,and ocean engineering.This equation will be reduced to the Korteweg–de Vries equation via using the perturbation analysis.We derive the corresponding vectors,symmetry reduction and explicit solutions for this equation.We readily obtain Bäcklund transformation associated with truncated Painlevé expansion.We also examine the related conservation laws of this equation via using the multiplier method.Moreover,we investigate the reciprocal Bäcklund transformations of the derived conservation laws for the first time.
Keywords:Boussinesq equation,perturbation and symmetry analysis,Bäcklund transformation,conservation laws
1.Introduction
The Boussinesq equation,good or classical and regularized or improved,plays an important role in fluid mechanics fields,scientific applications,and ocean engineering.The good Boussinesq equation given as
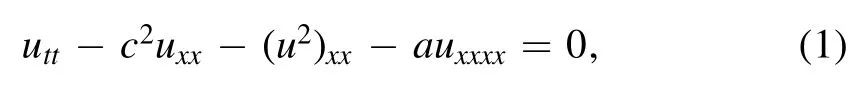
which describes the gravity induced surface waves as they propagate at constant speed in a canal of uniform depth.However,the regularized Boussinesq equation reads
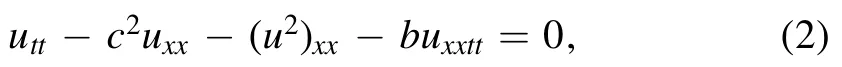
where the dispersion term uxxxxis replaced by the term uxxttthat improves the property of dispersion.Boussinesq equation[1] is commonly used to describe the long waves in shallow water.The classical equation(1)is completely integrable that gives multiple soliton solutions,whereas the improved equation(2)is not integrable,Both equations(1)and(2)have been studied intensively in the literatures [1–6] and some of the references therein.
Boussinesq-type equations have attracted many authors to conduct research work on these equations that arise in a variety of scientific and engineering fields.Boussinesq-type equations arise in many physical applications such as,sound waves in plasma,horizontal layer of material,nonlinear string[1–6] etc.It is well know that many nonlinear evolution equations including Boussinesq-type equations have soliton solutions [7–9].The bilinear method,in general,is a simple and straightforward approach to obtain soliton solutions[10–13].In addition,symmetry and conservation laws[14–23] play a key role in nonlinear mathematical physics fields.This is due to the fact that symmetry can be used to solve nonlinear evolution equations and find their new solutions.Conservation laws are very useful to interpret and explain many complex natural phenomena,such as momentum conservation,mass conservation,energy conservation and so on.For many nonlinear evolution equations,there are not only rich physical significance,but also elegant mathematical structure.
Recently,the relationship between the symmetry breaking and the energy dissipation of the infinite-dimensional nonconservative dynamic systems was explored [24],which is the theoretical foundation of the structure-preserving approach for the non-conservative dynamic systems and resulted in the broad applications of the structure-preserving method [25,26].This achievement established a bridge between the structure-preserving approach and the engineering problems.
In this work,we will study the Boussinesq equation
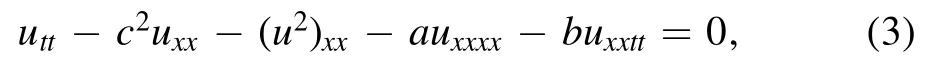
that involves two dispersive terms,namely uxxxxand uxxtt.It is clear that ifa≠ 0,b=0,This equation is reduced to the good Boussinesq equation (1) [2–4,6,27–30].However,forb≠ 0,a=0,it is reduced to the improved Boussinesq equation (2) [31,32].In [27] derived new similarity reductions of the Boussinesq equation (3).Moreover,authors of[28] studied non-classical symmetry reduction of the Boussinesq equation.the author in [29] considered the Lie symmetry,conservation laws and solitary wave solutions of the Boussinesq equation.
Concerning the mixed dispersive terms uxxxxand uxxtt,it is worth noting that Wang and Chen [33] studied the existence and uniqueness of the global solution for the Cauchy problem of the generalized double dispersion equation,where mixed dispersive terms,similar to what we used in (3),and they proved the blow-up result of the solution by using the concavity method and under some suitable conditions.They also emphasized that when the energy exchange between the surface of nonlinear elastic rod,whose material is hyperplastic (e.g.the Murnagham material),and the medium is considered,the double dispersion Boussinesq equation (3)can be derived from Hamilton principle,and it can also be obtained from the Euler equation for surface wave in irrotational motion.Moreover,Schneider and Wayne [34] considered the Boussinesq equation that models the water wave problem with surface tension that involves mixed dispersive terms,where this model can also be derived from the two dimensional water wave problem.In addition,Wang and Xue[35] studied the global solution for a generalized Boussinesq equation with two dispersive terms.More information about the double dispersive terms can be found in [33–35].
This paper is organized as follows,In section 2,we derive the Korteweg–de Vries(KdV)equation from extended Boussinesq equation (3) via using perturbation analysis.Symmetry analysis is employed to investigate this equation in section 3.In section 4,Bäcklund transformation associated with truncated Painlevé expansion are addressed.In section 5,conservation laws of this model(3)are presented.Reciprocal Bäcklund transformations of conservation laws are performed in section 6.Conclusions are displayed in the last section.
2.Perturbation analysis to derive KdV equation
Firstly,we use the following transformation

whereα,pare need to be fixed,that is to say,

Assuming thatu(i)→ 0(i=1,2,…)forξ→0,we expand this function into a series by
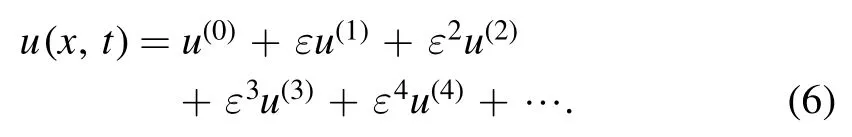
Substituting (6) into (3) gives
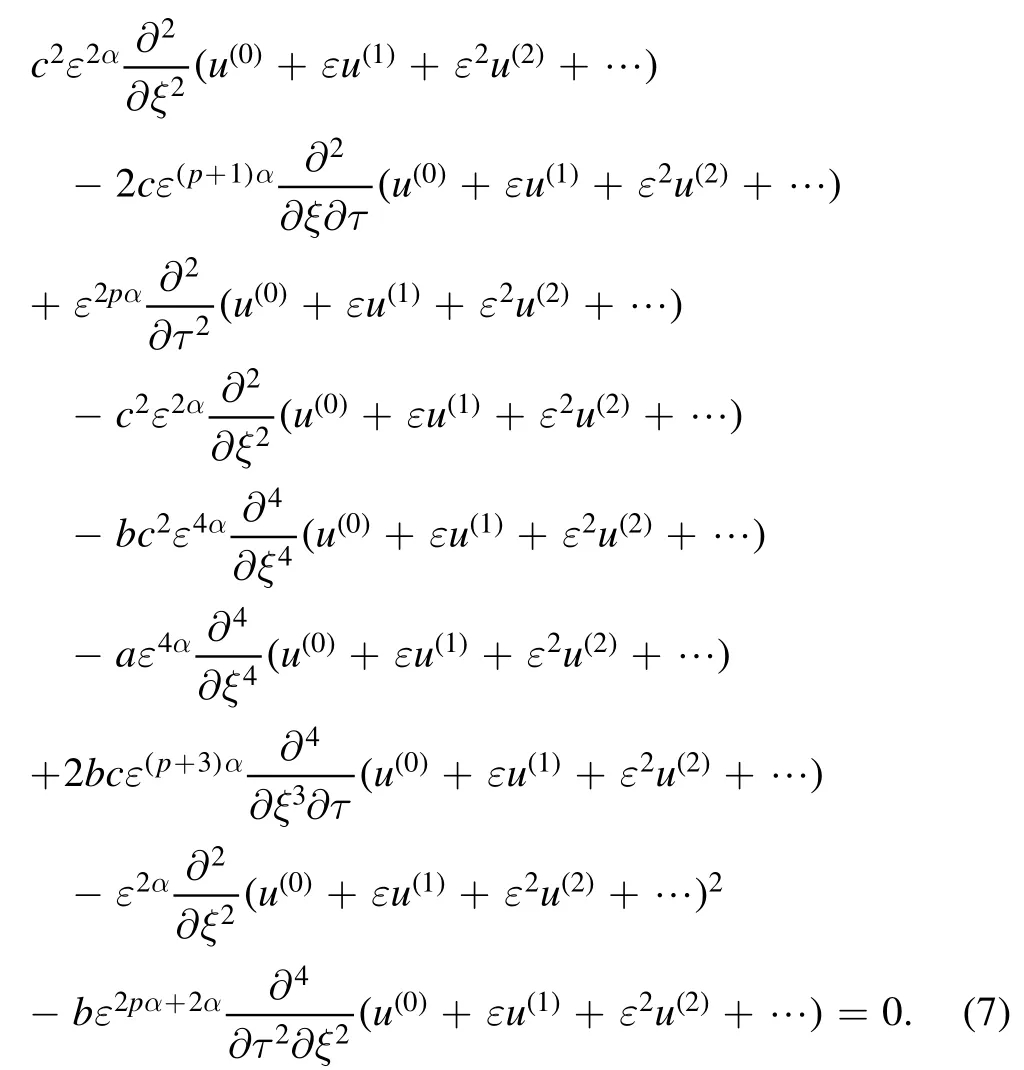
In order to arrive at our goal,we setu(0)=u(1)=0,and this gives(p+1)α= 4α,4α+2= 2α+4,which meansp= 3,α=1.Then (7) is reduced to
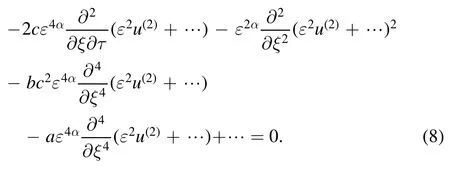
Therefore,we get
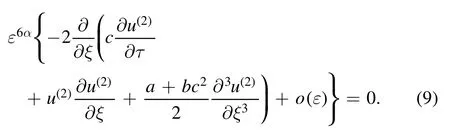
Consider the boundary conditionu(2)→0forξ→0,we get the nonlinear KdV equation
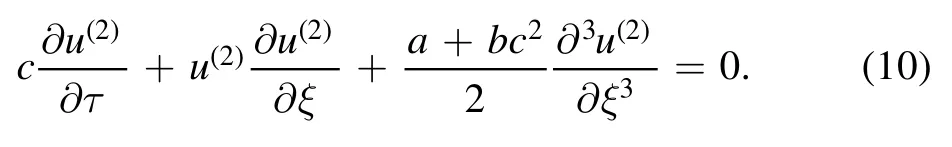
It is clear that,from extended Boussinesq equation,we also get the nonlinear KdV equation [6].
3.Generalized symmetry analysis,potential symmetry analysis and explicit solution
3.1.Generalized symmetry analysis
Now,we study equation (3) by following the generalized symmetry method as presented in the references([14,16,17]).A function σ is a symmetry of equation (3),if this function satisfies

where
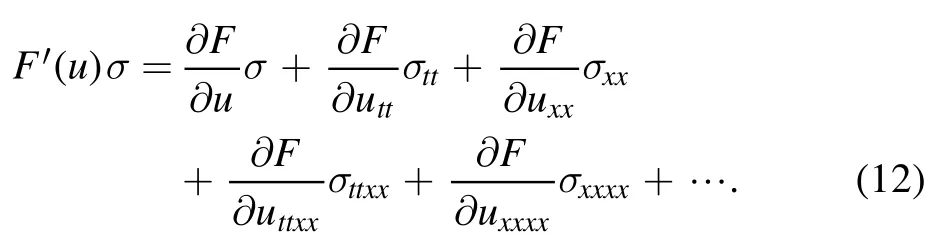
Therefore,we get the symmetry equation of equation (3) as
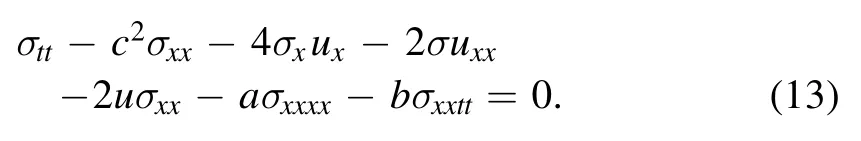
Setting σ equals to
where the coefficientsβi(i=0,1,2,3)are functions ofx,tand will be solved later.
Substituting (14) into (13) and using (3),we obtain the following results
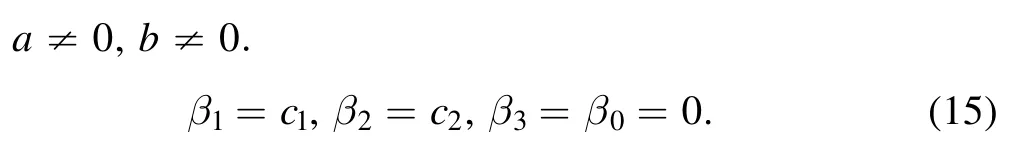
herec1,c2are arbitrary constants.
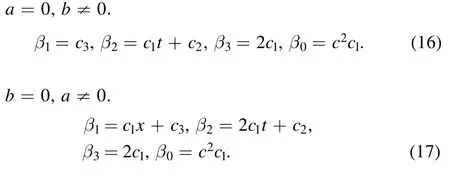
Therefore,we get symmetries for equations (15)–(17)respectively as

The equivalent vector expressions are obtained that read

In fact,fora≠ 0,b=0,it is in agreement with the obtained results for the Lie symmetry method reported in[29].Thus,it is just our special case.
3.2.Potential symmetry analysis
To conduct the potential symmetry analysis,we first rewrite(3) as conservation laws formTt+Xx=0,
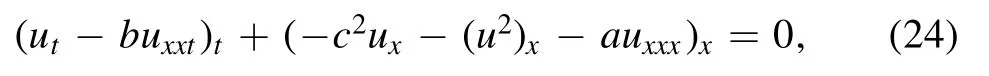
or
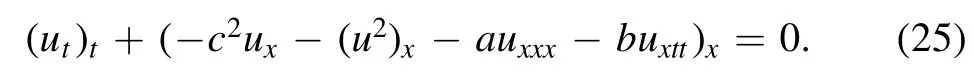
In order to derive the Lie point symmetry,for (24) we set
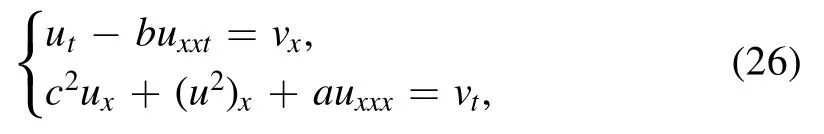
and for (25) let
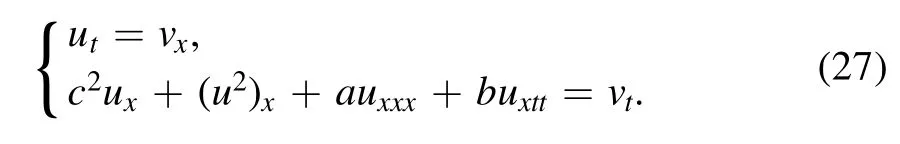
Consider the following vector

Based on the symmetry method [14,15,17–22],we get the same results for (24) and (25)
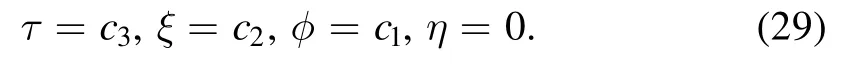
Based on the potential symmetry method [15],we found that these equations (24) and (25) do not have any potential symmetries.
3.3.Explicit solution via traveling wave transformation
Using traveling wave transformation,we set the invariant and invariant function

Substituting (30) into (3) leads to
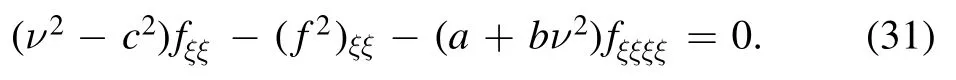
Integrating equation (31) once gives

Integrating equation (31) again yields

whereA,Bare the integral constants.IfA=B= 0,it is a reduced equation as given in [29].On the other hand,equation (33) gives the following form solutions

Substituting (34) into (33),one gets

Comparing coefficients of (35),we have

By considering the other coefficients of(35),ifn≥ 2,we obtain

Therefore,we rewrite the power series solution as follows

Thus,substitutingξ=x−νtinto (38) gives
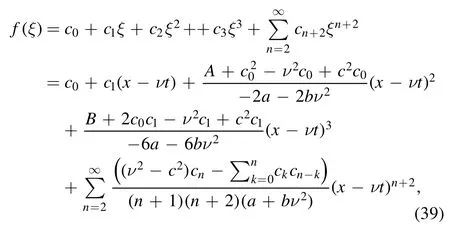
whereci(i= 0,1)are arbitrary consta nts.
Let the integration constant B equal to zero and multiplyfξ,integrate equation (33) once,we derive
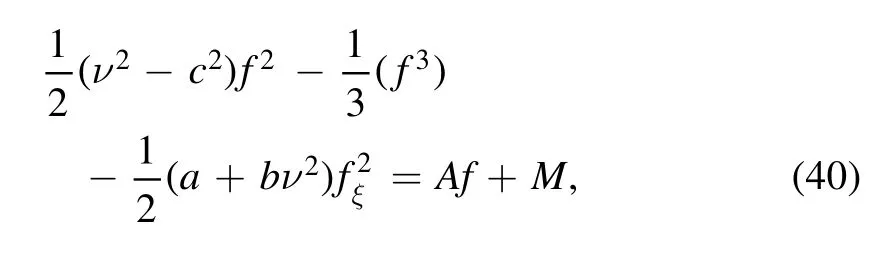
where M is the integral constant.Rewrite equation (40)
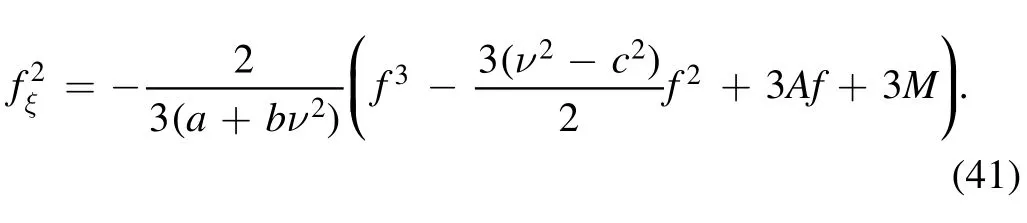
Consider the equation

Consider the three solutions to this equation justify the inequalityu1≥u2≥u3,therefore,one getsu1+u2+Also,
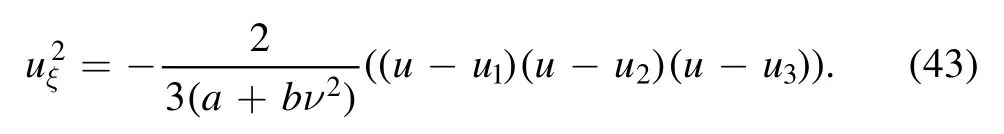
As a result we obtain the solution as

where

Ifk→0,we get trigonometric solution.However,fork→1,we get a solitary wave solution
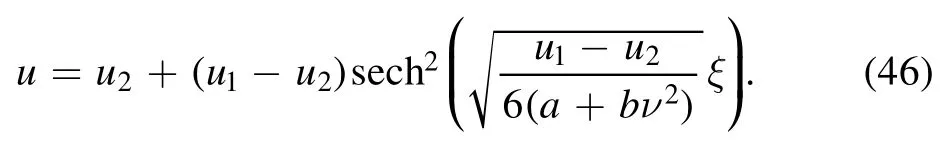
In particular,setA=we have
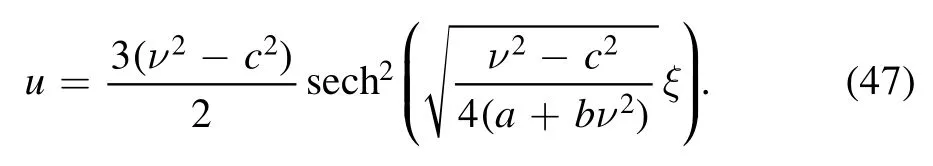
It is clear that equation (41) includes a great number of solutions,such as trigonometric solutions,Jacobi elliptic solutions,hyperbolic solutions and so on.Here,we do not list them in details.
4.Bäcklund transformation associated with truncated Painlevé expansion
Based on the assumption presented earlier in section 2,we set

Inserting equation (48) into (3),we get polynomials of different orders of f,all coefficients of different orders should be zero.Therefore,from coefficient:f−6,one gets
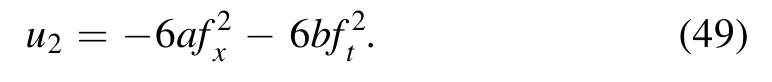
And then,substitute equation(49)into coeffciientf−5,one fnids

Substituting equations(49)and(50)into coefficient off−4,one obtains
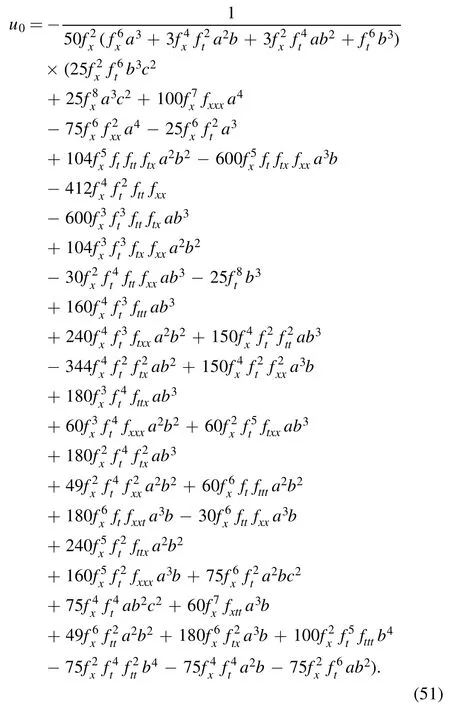
Substitute equations (49)–(51) into coeffciient off−3,one derives an equation with regard to f.In other words,f needs to satisfy the equation of this coeffciientf−3(see appendix).
Therefore,we get the following theorems is a solution of(3),where u0,u1and u2are given by equations (49)–(51)respectively.
Theorem 1.Iffsatisfies the equation of the coefficientf−3,thenu0is a solution of (3).
Theorem 2.Iffsatisfies the equation of the coefficientf−3,then

Theorem 3.u0is a auto Bäcklund transformation.
Proof: From coefficient f0,we can find that
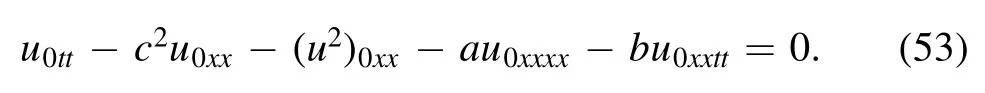
5.Conservation laws
In this section,we study conservation laws of equation(3)by using the multipliers method [15].One should get the multipliers,
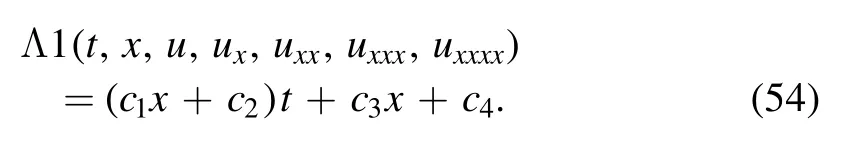
Therefore,we get
Theorem 4.For the multiplierxt,we have
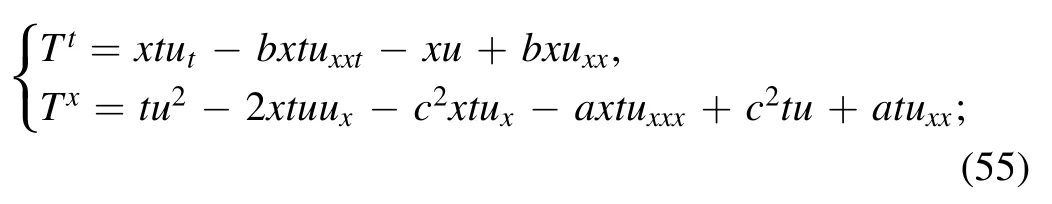
On the basis of the multipliert,we get
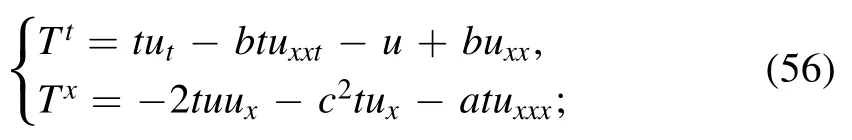
For the multiplierx,we have

As to the multiplier 1,we get
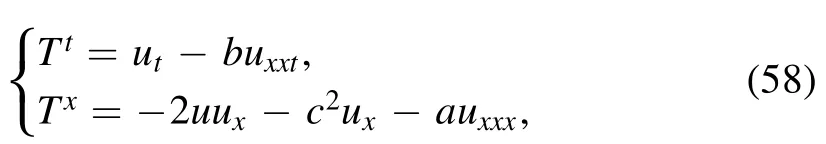
or
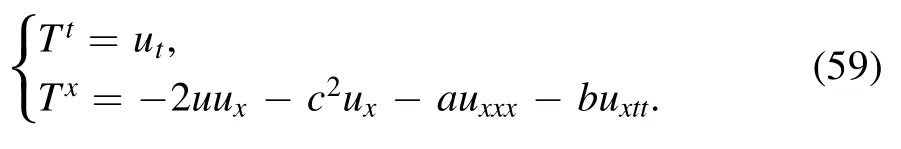
6.Reciprocal Bäcklund transformations of conservation laws
Based on the method addressed in [36],we consider the reciprocal Bäcklund transformations of conservation laws.
Theorem 5.[36] The conservation law
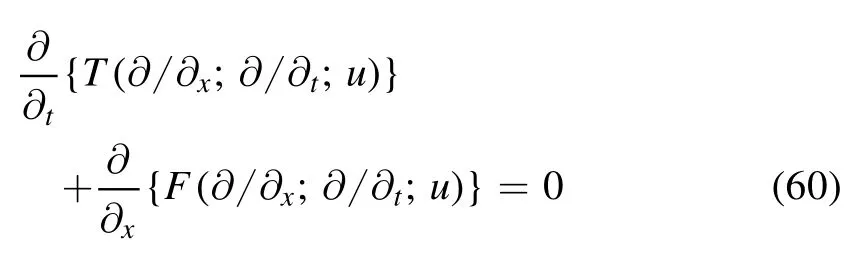
is transformed to the reciprocally associated conservation law
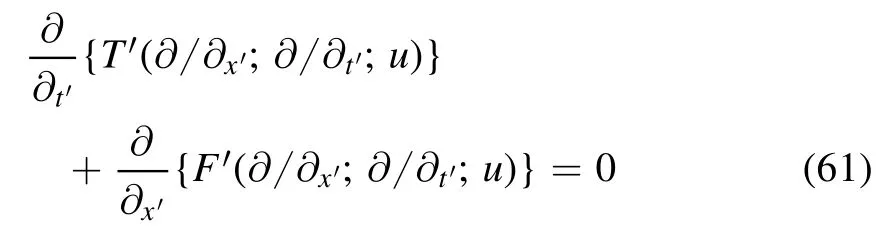
by the reciprocal transformation
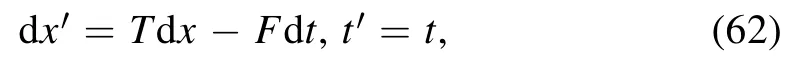
where

From equations (62) and (63),we get
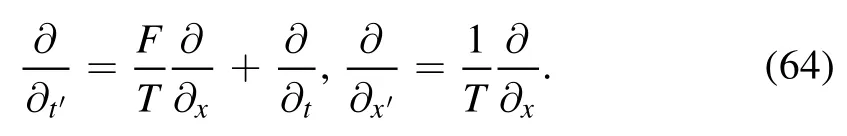
Now,based on the Theorem 5,we will deal with reciprocal Bäcklund transformations of conservation laws.
As to the multiplier 1,we obtain
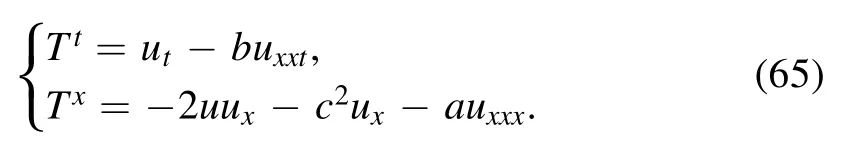
Therefore,conservation laws (65) transform to the following form:
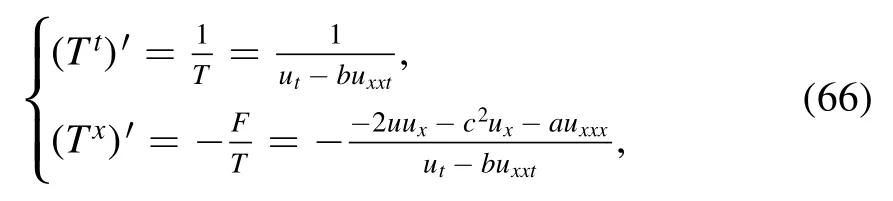
or equivalently

And similarly,we can get the remaining reciprocal Bäcklund transformations of conservation laws.
For the multiplier xt,we derive
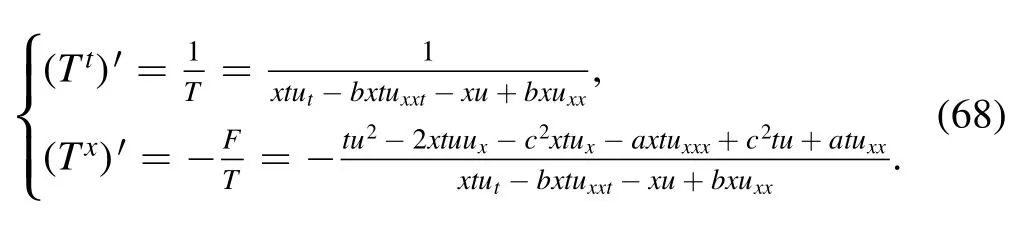
As to the multiplier t,we find
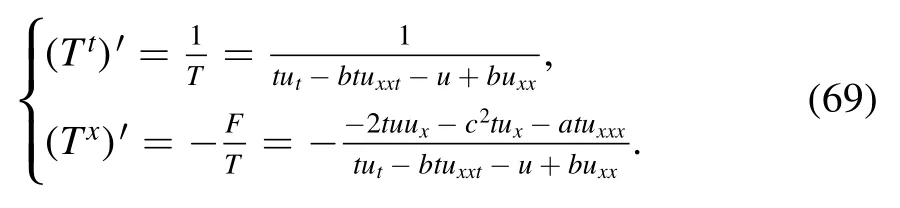
For the multiplier x,we have
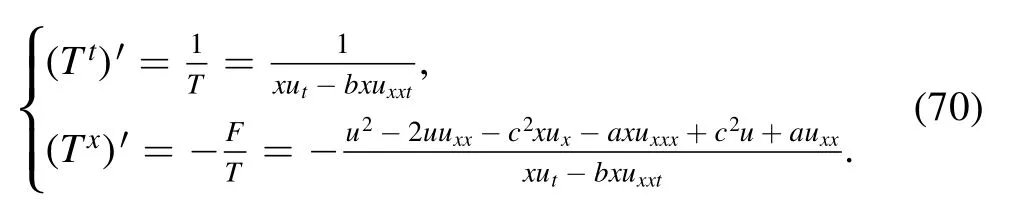
As to the multiplier 1,one can get
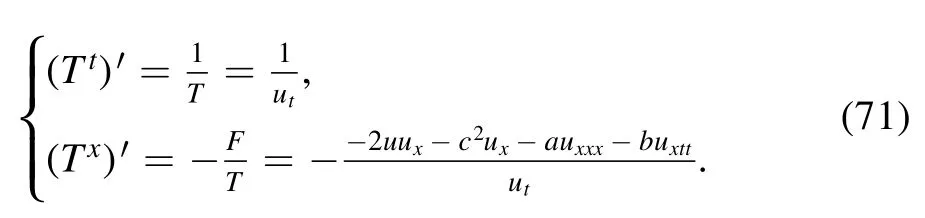
7.Conclusions
In the present work,the extended Boussinesq equation (3),that involves two dispersive terms,is investigated.From this equation,we derived the KdV equation using the perturbation analysis.Then,based on the generalized and potential symmetry,the corresponding symmetries and vector fields are performed.Some explicit solutions are also given.In addition,Bäcklund transformation associated with truncated Painlevé expansion are studied.Meanwhile,conservation laws also presented.After this,reciprocal Bäcklund transformations of conservation laws are performed for the first time.In this paper,we just considered the constant coefficients case.The obtained results will be employed for further works in the future.
Acknowledgments
This work is supported by Natural Science Foundation of Hebei Province,China (Grant No.A2018207030),Youth Key Program of Hebei University of Economics and Business(2018QZ07),Key Program of Hebei University of Economics and Business (2020ZD11),Youth Team Support Program of Hebei University of Economics and Business.National Natural Science Foundation of China (Grant No.11 801 133).
Appendix
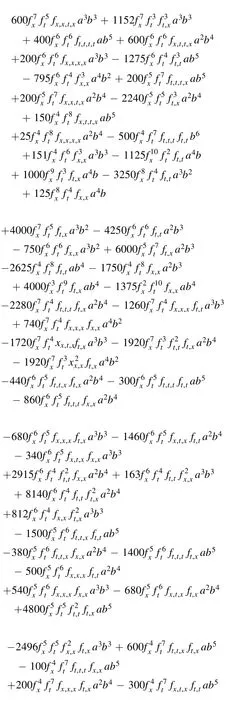
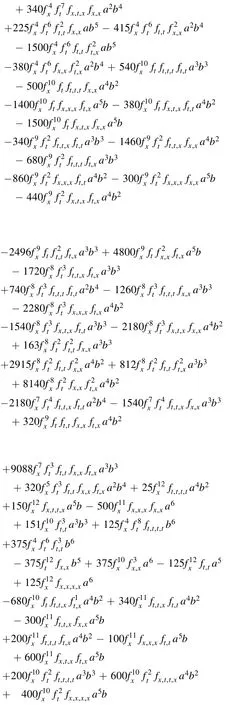
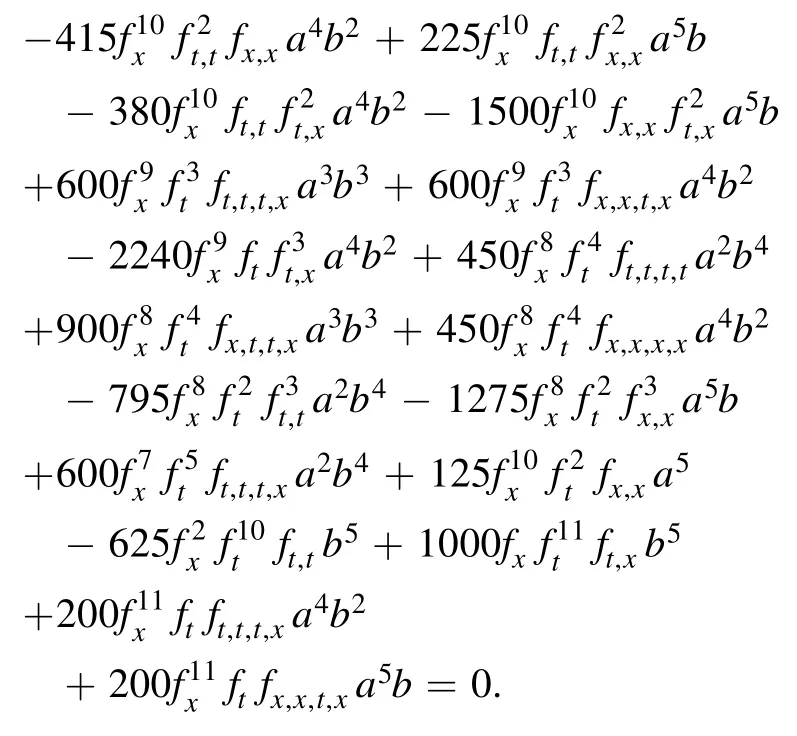
 Communications in Theoretical Physics2021年4期
Communications in Theoretical Physics2021年4期
- Communications in Theoretical Physics的其它文章
- Charged torus-like black holes as heat engines
- Pure annihilation decays of and in the PQCD approach
- Exploring the latest Pantheon SN Ia dataset by using three kinds of statistics techniques
- Hawking temperature of Kerr anti-de-Sitter black hole affected by Lorentz symmetry violating*
- The vacancy defects and oxygen atoms occupation effects on mechanical and electronic properties of Mo5Si3 silicides
- Deposition pattern of drying droplets
