三次非线性忆阻器的双端口建模与特性分析

曹 伟 ,乔金杰 ,赵丽娜 ,崔 弘

(1.齐齐哈尔大学计算机与控制工程学院,黑龙江齐齐哈尔 161006;2.齐齐哈尔大学经济与管理学院,黑龙江齐齐哈尔 161006)

1971 年美国华裔科学家蔡少棠教授从物理学对称性角度,首先提出了忆阻器的存在[1],全称记忆电阻器(Memristor)。传统电阻是线性无源二端口元件,而忆阻器体现的是磁通量与电荷之间的关系,其阻值随两端输入的电流或电压而变化,而且在断电情况下能保持以往的值不变,只有输入反向电流时才会被推回。因此,忆阻器是具有非易失性的非线性无源二端口电路元件。但由于当时仅从数学上推导得到的忆阻器,缺少实验支撑,因此忆阻器提出后的30 多年,并没有引起研究者的足够重视。直到2008 年5 月,在《Nature》 杂志上发表了美国惠普实验室研制出的二氧化钛忆阻器实物模型[2-3],才引起了人们对忆阻器研究的极大兴趣[4]。

正因为忆阻器是具有记忆功能的非线性新型电路元件,因此在混沌电路[5-6]、人工神经网络[7-8]、非易失性存储[9]和模拟电路[10-11]等众多领域有着广泛应用前景。但由于忆阻器是纳米级元件,加之受限于严格的实验条件,能够将其物理属性完全体现出来的标准元件到目前为止还是难以获得,精确电气特性实验数据的获取也较难[12]。因此为了更好地促进对忆阻器及其应用研究,建立有效的仿真模型尤为重要,且成为了一个研究热点。文献[13-14]利用文献[15-16]建立的忆阻器模拟电路仿真器(Simulation Program with Integrated Circuit Emphasis,SPICE)取得了一些应用研究成果。文献[17]基于Simulink 建立了两种不同窗函数的惠普忆阻器的仿真模型。2009 年文献[18]给出了忆阻器和忆容器的分阶段线性函数模型,分析了记忆元件的电路特性,但没有建立仿真模型。文献[19]通过对文献[18]中给出的分段线性函数忆容器数学模型的分析,基于Simulink 构建了忆容器的仿真模型,但该仿真模型只实现了数学模型中的分段线性函数部分,并没有体现出数学模型中的阶跃函数,从而该仿真模型没能反映出忆容值依赖于历史状态的特性。为弥补文献[19]中的不足,文献[20]在文献[19]建立的仿真模型基础上,建立了能够实现阶跃函数功能的忆阻器、忆容器和忆感器的Simulink 输入输出仿真模型,正确反映出了忆阻值、忆容值和忆感值的记忆特性和历史状态有关的特性,但文献[20]建立的输入输出仿真模型不方便与其他二端口元件连接。为了便于与其他二端口元件相结合,扩大忆阻器的应用范围,文献[21]基于Simulink 建立了双曲正弦函数忆阻器的双端口模型,遗憾的是该文献也没能体现出忆阻器阻值对历史状态的依赖性。

因此,为了使基于Simulink 建立的忆阻器仿真模型便于与双端口电路元件直接连接,并能体现出忆阻器阻值对历史状态的依赖性,本文结合文献[20]和文献[22]的思路,通过分析压控型忆阻器的数学模型,利用忆阻器的输入电压和上下限饱和度,设计了一种带有单位阶跃函数的三次非线性函数,以此来表示忆阻器的阻值变化率,并通过引入受控电流源和交流电压源的方法构建了基于Simulink 的双端口模型。该模型不仅能体现出忆阻器的记忆特性和历史状态有关的特性,而且建立的三次非线性函数忆阻器的双端口模型更便于搭建忆阻相关电路,扩大忆阻器的应用范围。最后,通过对建立的双端口模型输入不同信号的仿真实验,验证了所建立的双端口模型的有效性。

1 忆阻器的数学模型与基本特性

1.1 忆阻器的数学模型

蔡少棠教授在1971 年提出忆阻器概念时,指出忆阻器描述了磁通量φ与累积电荷q之间的某种关系,其数学定义可表示为[1]:

忆阻器可分为荷控型和磁控型。当式(1)是磁通的单值函数时即为磁控型忆阻器,也称为压控型忆阻器,可由式(2)表示:

式中:qM为流经忆阻器的电荷量;vM(t)为加在忆阻器两端的电压;iM(t)为通过忆阻器的电流;φM(t)为忆阻器的磁通量;WM为忆导值。变量的下标M 表示该变量与忆阻有关。

当式(1)是电荷的单值函数时即为荷控型忆阻器,也称为流控型忆阻器,可由式(3)表示:

式中:RM为忆阻值。

忆阻器是一个基本的非线性无源二端口元件,可作为第四种电路元件,与普通电阻器、电感器和电容器一起构成了电路理论的完备性。

文献[18]中在将忆阻器的概念推广至忆容器和忆感器时,给出了记忆元件的一个通用数学表达式,如式(4)所示。

式中:u(t)和y(t)分别为记忆元件的输入和输出;x为记忆元件的状态变量;g为广义响应函数;f为连续向量函数。当u(t)取流经忆阻器的电流,y(t)取加在忆阻器的两端电压时,流控型忆阻器的通用数学模型可表示为:

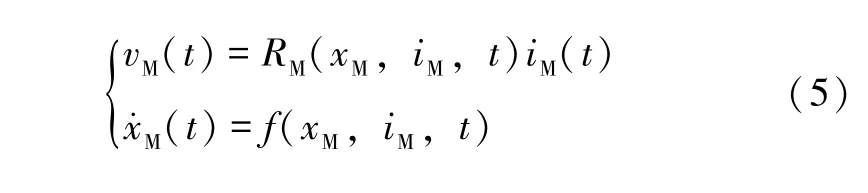
式中:xM为忆阻器系统的无量纲状态变量。同样,当u(t)取加在忆阻器的两端电压,y(t)取流经忆阻器的电流时,则压控型忆阻器的通用数学模型可表示为:

2008 年美国惠普实验室研制出一种纳米级忆阻器的物理模型[2],自此人们针对惠普实验室的二氧化钛忆阻器展开众多研究,建立了线性杂质漂移模型、窗函数模型、分段函数模型、三次非线性模型、积分模型等数学模型。

1.2 忆阻器的基本特性

忆阻器具有如下特性[23]:加在忆阻器两端输入电压与流经忆阻器的电流呈滞回环关系,且滞回环的宽度随输入正弦电压幅值的增加逐渐变宽,随输入正弦电压频率的增加而逐渐变窄,直至一条直线。

同时,从式(6)可以看出,当忆阻器的输入电压vM(t)=0 时,其输出必定为零,即iM(t)=0,也就是说忆阻器具有过零属性。因此,当用一定频率的过零周期电压作为忆阻器的输入信号时,其电压和电流的特性曲线一定是过坐标零点的滞回环曲线。2008 年美国惠普实验室利用研制出的忆阻器物理模型,通过实验进一步验证了忆阻器的上述特性[2]。

2 忆阻器双端口模型的建立

2.1 基于受控源的双端口模型设计

由于基于Simulink 建立的输入输出模型不方便与众多双端口电路元件直接连接,因此本文建立一种三次非线性函数忆阻器的双端口模型。

本文通过分析忆阻器的通用数学模型,利用忆阻器上下限饱和度和输入电压,设计带有单位阶跃函数的三次非线性函数,以此来表示忆阻器的阻值变化率。即给定忆导WM(xM,vM,t),设计阻值变化率(t) 的表达式如式(7)所示:

则式(6)可用式(8)和式(9)表示为:

式中:α和β为常数;R1为忆阻器的上限饱和度;R1为忆阻器的下限饱和度;θ为单位阶跃函数;xM为忆阻器阻值。

为实现忆阻器的双端口建模,通过引入受控电流源和交流电压源的方法建立基于Simulink 的双端口模型。因为式(8)和式(9)为压控型忆阻器的数学模型,因此根据式(8)选择受控电流源,并将式(8)的电流作为受控电流源的控制信号。式(8)通过交流电压源两端电压、积分器1、倒数模块和乘法器4 实现。式(9)表示的忆阻器阻值变化率通过交流电压源两端电压、乘法器1-3、增益1-2、加法器、常数模块1-4、开关1-2 实现。将积分器1 的输出通过阶跃函数后反馈到积分器1 的输入端,实现忆阻器的记忆功能。给定积分器1 有效初始值,则式(9)通过积分器1 后便可得到忆阻器阻值xM。

按照上述方案建立的双端口模型如图1 所示。模型中的4 个常数模块和2 个开关模块实现了式(9)中单位阶跃函数功能。其中阶跃函数的0 和1 两个状态,分别由0 和1 两个常数模块表示。将xM与开关1 的阈值R1比较,当xM＞R1时,开关1 输出为1,否则为0;将xM与开关2 的阈值R2比较,当xM＜R2时,开关2 输出为1,否则为0。这样,阶跃函数在式(9)中的作用得以实现,同时还体现出了忆阻器阻值依赖于历史状态的特性,即忆阻器的记忆特性得到正确表征。

图1 忆阻器的双端口模型与验证电路Fig.1 Dual port model of the memristor and its verification circuit

2.2 忆阻器双端口模型的特性分析

为验证双端口模型的有效性,按照图1 所示的验证电路,给双端口模型接入交流电压源和示波器进行测试实验。模型中的参数设置如下:正弦交流电压源的幅值为vm,频率为f,即加在忆阻器两端的电压为vM(t)=vmsin(2πft);增益1 取α=400 Ω·V-1·s-1,增益2 取β=400 Ω·V-3·s-1,开关2 阈值R2=500 Ω,开关1 阈值R1=20 Ω,积分器1 初始值取为70 Ω,电力系统图形化用户分析界面模块选为连续型,其余设置都取默认值,计算步长设为0.001 s。示波器1显示的是忆阻器的电压vM和电流iM关系曲线,示波器2 显示的是忆阻器的电压vM和忆导WM关系曲线,示波器4 显示的是忆阻器的阻值变化曲线,图1 中右下角的积分器2、积分器3 和示波器3 是为了获取电荷-磁通曲线而添加的,如果不需要获取该曲线可以省略该部分。

下面分别讨论双端口模型特性受输入电压的频率、幅值和波形的影响情况。

(1)正弦输入电压的频率对模型特性的影响

假设输入双端口模型的正弦交流电压的频率f分别为0.5,5,30 Hz,而电压的幅值vm=1.0 V 保持不变,此时由示波器1 测得模型的电压与电流的关系曲线如图2 所示。由图2 可以看出,当电压频率逐渐增加时,电压-电流的滞回环逐渐变窄,当f增加到一定值时滞回环则变为一条直线。

图2 输入电压的频率对电压-电流曲线的影响Fig.2 Influence of the input voltage frequency on the voltage and current curve of the memristor

(2)正弦输入电压的幅值对模型特性的影响

假设输入双端口模型的正弦交流电压的幅值vm分别为0.2,0.6,1.0 V,而电压频率f=0.5 Hz 保持不变,此时由示波器1 测得模型电压与电流关系曲线如图3 所示。由图3 可以看出,当电压幅值逐渐增加时,电压-电流的滞回环逐渐变宽。

(3)输入电压波形不同时的双端口模型特性

当双端口模型输入幅值vm=1.0 V,频率f=0.5 Hz 且过零的周期波(正弦波、锯齿波、方波)电压时,电压-电流特性曲线和电压-忆导特性曲线如图4 所示。由图4 可以看出,当双端口模型输入任何过零周期波时,都能得到过坐标零点的滞回环曲线。

图3 输入电压的幅值对电压-电流曲线的影响Fig.3 Influence of the input voltage amplitude on the voltage and current curve of the memristor

此外,在忆阻器双端口模型输入幅值vm=1.0 V,频率f=0.5 Hz 的正弦波交流电压时,由示波器3 和示波器4 分别测得电荷-磁通变化情况和忆阻器阻值随时间的变化情况,如图5 和图6 所示。由图5 可以看出,电荷与磁通之间存在着非线性关系,表明了忆阻的非线性,由图6 也可以看出,忆阻器的阻值随时间在上下饱和度之间做非线性变化。

根据上述实验结果可知,建立的双端口忆阻器模型完全符合忆阻器的定义和基本特性,证实了双端口忆阻器模型的有效性。

3 结论

本文在分析忆阻器通用数学模型基础上,通过引入受控电流源和交流电压源的方法建立了一种三次非线性函数忆阻器的双端口模型。并在不同输入信号下对建立的模型进行了仿真实验,得到了双端口模型在不同输入信号时,电压与电流呈现出的滞回环的变化规律,且变化符合忆阻器的基本特性,验证了双端口模型的有效性。该模型不仅能体现出忆阻器的记忆特性和历史状态有关的特性,而且建立的三次非线性函数规律忆阻器双端口模型更便于搭建忆阻相关电路,扩大了忆阻器的应用范围。按照本文设计思路同样可以设计三次非线性函数忆容器和忆感器的双端口模型。

图4 输入电压波形不同时的双端口模型特性Fig.4 Dual port model characteristics when input voltage waveforms are different

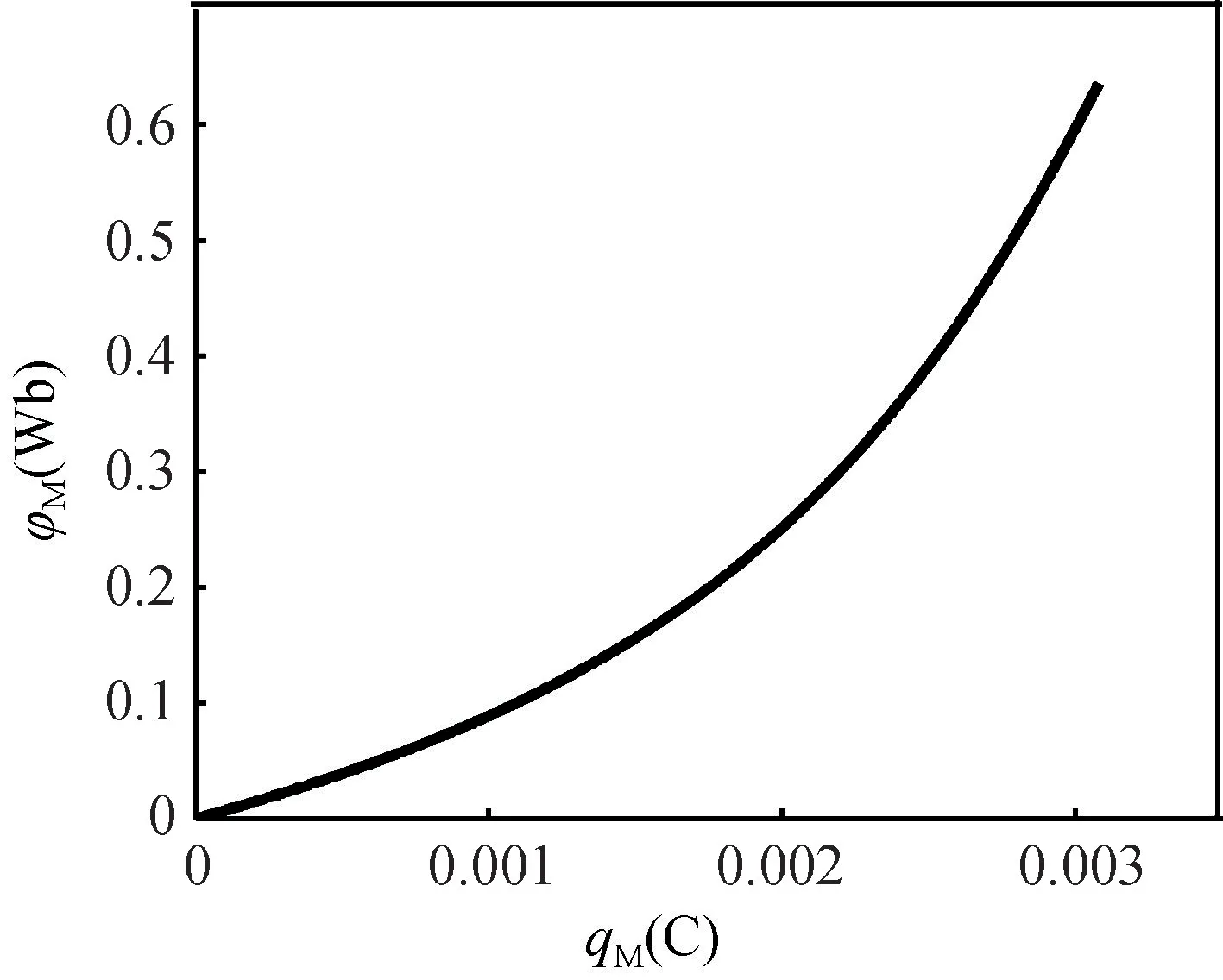
图5 忆阻器的电荷-磁通变化曲线Fig.5 qM-φMcurve of the memristor

图6 忆阻器的阻值随时间的变化曲线Fig.6 Variation curve of resistance of memristor with time