直左复线有轨电车干线可变带宽绿波模型

王昊，黎冬平，孙国鼎

(1.东南大学，a.交通学院，b.城市智能交通江苏省重点实验室，c.现代城市交通技术江苏高校协同创新中心，南京211189；2.上海市城市建设设计研究总院(集团)有限公司，上海200125)

0 引言

现代有轨电车采用地面敷设式轨道，在平面交叉口处与机动车存在通行权冲突，交通组织方式较为复杂，特别是对于直行和转向多线共轨的有轨电车网络，轨道在交叉口处分叉进一步增加了地面交通组织和控制的复杂度。如果缺少合理、有效的信号控制方案，将导致有轨电车和社会车辆通行权不协调，增加社会车辆和有轨电车的整体延误，严重影响干线系统的通行效率。因此，分析直行与转向复线共轨的有轨电车运行特点，构建兼顾复线有轨电车和社会车辆通行效率的干线绿波方案设计方法，既具有理论意义，又具有实用价值。

国外学者对干线信号协调控制的研究较早，最经典的成果是 MAXBAND 绿波模型和MULTIBAND绿波模型。Little等[1-2]在总结前人研究成果的基础上，提出半整数相位差(half-integer)信号协调，加入左转信号相位影响因素，基于双向交通流量比分配带宽，建立了混合整数线性规划模型——MAXBAND，通过分支定界法寻求最优解，从而确定最佳的双向最大带宽、信号周期、相邻信号相位差、行驶时间及左转相位设计方案等。Gartner 等以MAXBAND 模型为基础，即根据交叉口间各路段的交通流量、交通条件及交通需求给予不同路段不同带宽值，建立了MULTIBAND 模型[3]，运用启发式分解算法提高了混合整数线性规划问题最优解的求解效率[4]，并使模型能够适应实时信号协调控制优化的要求[5]。Jeong等[6]提出了基于MAXBAND 的TRAMBAND 模型，在同一信号控制背景下分别生成路中式有轨电车绿波、社会车辆绿波，并通过实例验证该模型可有效降低社会车辆、有轨电车在交叉口的延误。Zhang 等[7]对MUTILIBAND 模型进行了改进，取消了模型中同一路段内绿波必须对称的约束，提出非对称绿波模型AM-BAND。

国内学者王殿海等[8]提出了经过修正的绿波带宽数解法以及实际交叉口与理想交叉口的匹配方法。戴光远等[9]在MAXBAND模型的基础上，针对公交车的停站特性及通行需求，将公交车站作为绿波分区节点，突破了传统绿波算法中同一路段内绿波带宽不可变的限制，提出了分段式绿波模型。周洋帆等[10]提出了考虑运行图约束的有轨电车干线信号协调优化模型，使有轨电车停站时间和站间运行时间与运行图一致。

综上所述，国内外对绿波的研究成果主要集中于社会车辆以及常规公交车辆、有轨电车的干线绿波优化，缺少对同时存在直行和转向的复线共轨式有轨电车的干线绿波的研究。鉴于此，本文针对存在直左复线有轨电车的干线系统，改进经典MULTIBAND模型，在满足有轨电车绿波带宽需求的基础上，以最大化社会车辆绿波带宽为目标，建立综合考虑直左复线有轨电车绿波系统和社会车辆绿波系统的干线交通信号协调控制模型。

1 直左复线有轨电车基本特征

1.1 有轨电车线路特征

图1为直行线路和左转线路的有轨电车在干线道路共轨的路中式布局，图中Sk为交叉口k。有轨电车布设在路中，在路段上拥有独立路权，与社会车辆之间互不干扰，只有在交叉口处与社会车辆混行；干线分为上、下行方向，有轨电车线路1为直行线路，有轨电车线路2 为左转线路，该线路上行有轨电车在干线的第k个交叉口处通过左转由干线转到相交道路上，下行有轨电车在该处通过右转由相交道路转至干线道路。

图1 直行与左转有轨电车复线共轨布局示意Fig.1 Layout of arterial with straight and left-turn tram lines

1.2 干线交叉口相位设计

在路中式有轨电车布局中，直行线路有轨电车仅与直行机动车不存在冲突，可以共用通行相位。左转线路有轨电车与干线双向左转机动车以及干线同向直行机动车不存在冲突，可以共用相位。为扩大绿波解的可行域，采用早启迟断式相位方案。图2为干线上、下行方向社会车辆左转通行相位和直行通行相位的4 种典型组合。使用上划线表达下行方向的变量。为求解方便，将所有关于时间的变量都表示为信号周期时长C的倍数。i表示干线上行方向上第i个交叉口的序号。直行有轨电车和转向有轨电车利用与之无冲突的社会车辆相位通过交叉口。li、分别为第i个交叉口上、下行方向左转相位的绿灯时长；gi、分别为第i个交叉口上、下行方向直行相位的绿灯时长；Ri为第i个交叉口支路方向绿灯时长。

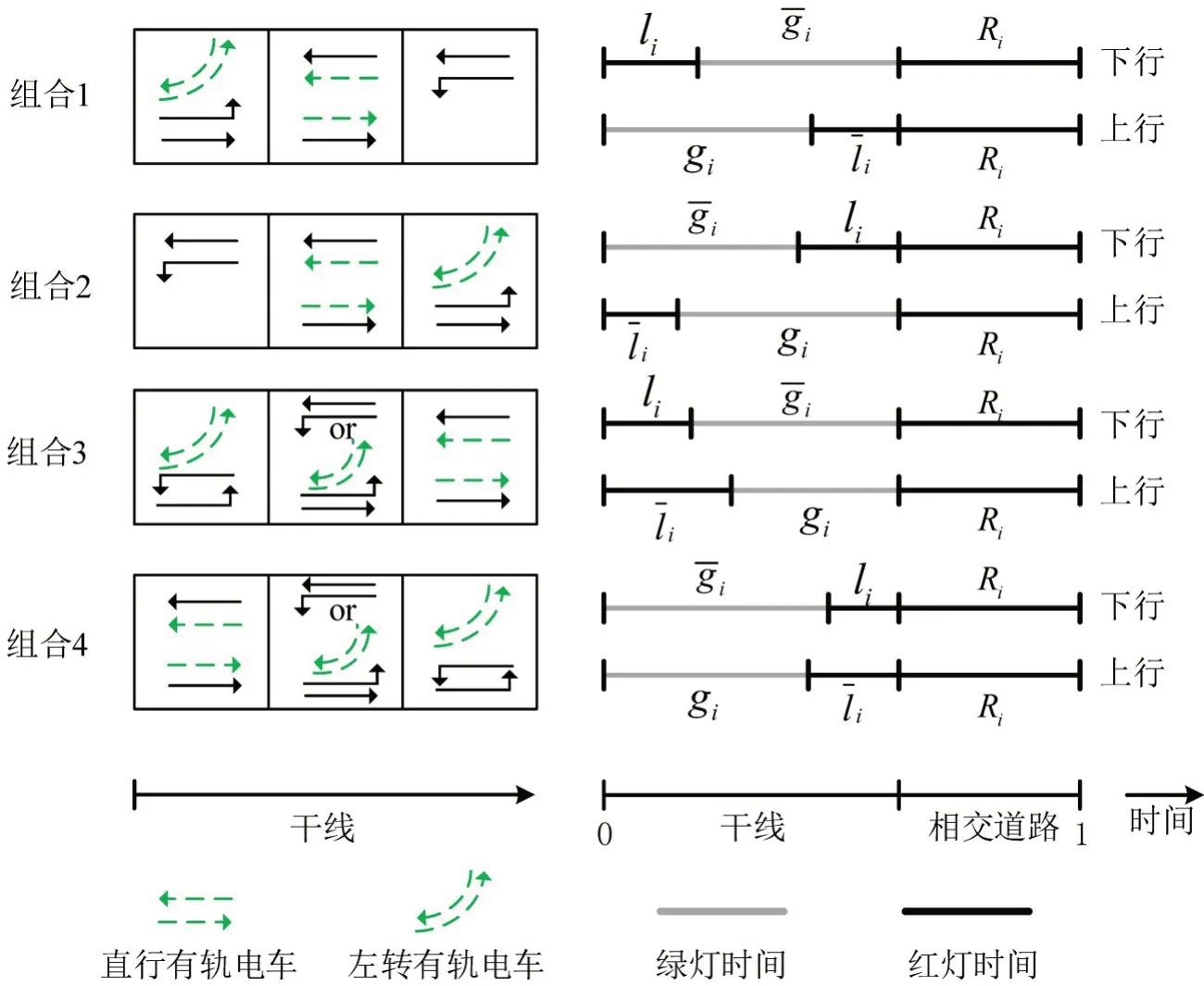
图2 干线交叉口信号相位组合Fig.2 Schemes of traffic phase for intersections in arterial

令Δi表示第i个交叉口上行红灯时间中心时刻到下行红灯时间中心时刻的时间差值，并引入0-1变量，则不同相位组合方案下的Δi为

式中：δi，均为0-1 变量，表1为4 种相位方案的变量取值情况。

表1 不同相位组合对应的δi 和Table 1 δi and for various phase schemes

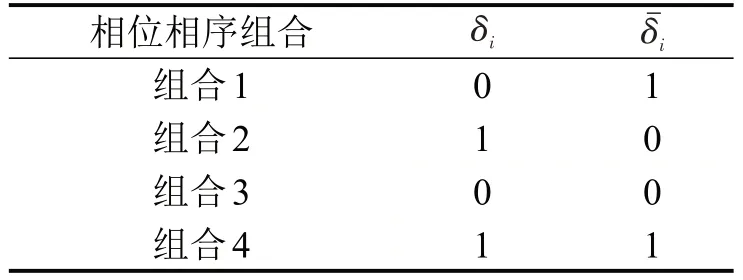
表1 不同相位组合对应的δi 和Table 1 δi and for various phase schemes

相位相序组合组合1组合2组合3组合4 δi 0 1 0 1 δˉi 1 0 0 1

2 考虑有轨电车绿波的干线信号协调控制模型

考虑直左复线有轨电车绿波的干线协调控制模型包含5 个方面：社会车辆绿波的约束条件，直行线路有轨电车绿波的约束条件，左转线路有轨电车绿波的约束条件，社会车辆绿波与双线路有轨电车绿波的交互约束条件，以及模型目标函数的设计。

2.1 社会车辆绿波约束条件

图3为干线社会车辆绿波时空图，根据MULTIBAND 模型[3]，社会车辆绿波的基础约束条件为

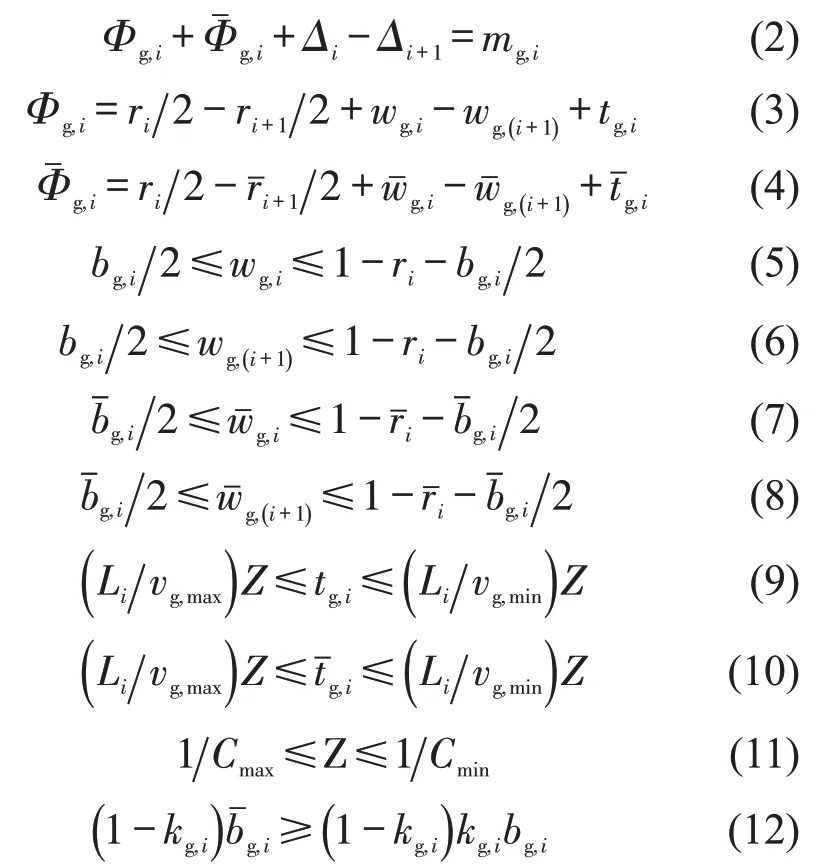
式中：Φg,i()为交叉口Si+1与Si社会车辆上(下)行红灯中心时刻的时间差(cycle)；ri()为交叉口Si上(下)行社会车辆直行相位的红灯时长(cycle)；wg,i()为交叉口Si上(下)行社会车辆绿波带中线与上(下)行红灯时间右(左)侧的时间差(cycle)；tg,i()为上(下)行社会车辆在交叉口Si与Si+1之间的行程时间(cycle)；bg,i()为上(下)行社会车辆在交叉口Si与Si+1之间的绿波带宽(cycle)；Cmax(Cmin)为周期时长的最大(最小)值(s)；vg,max(vg,min)为社会车辆平均行驶车速的最大(最小)值(m·s-1)；Li为交叉口Si与Si+1之间的路段长度(s)；kg,i为社会车辆上、下行绿波带宽的影响参数，由上、下行交通量的比值表示；Z为周期倒数(cycle·s-1)。

图3 社会车辆绿波系统时空图Fig.3 Time-space diagram of general traffic

2.2 有轨电车直行线路约束条件

类似于社会车辆绿波系统，有轨电车直行线路绿波系统的基础约束条件可根据图4进行推导，即

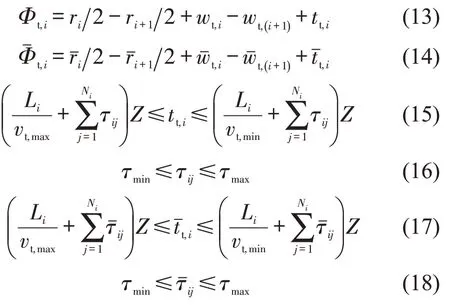
式中：Φt,i()为直行线路有轨电车绿波系统中交叉口Si+1与Si的上(下)行红灯中心时刻的时间差(cycle)；wt,i()为交叉口Si处直行线路有轨电车上(下)行绿波带前(后)锋与上(下)行红灯时间右(左)侧的时间差(cycle)；tt,i()为上(下)行直行线路有轨电车在交叉口Si与Si+1之间的行程时间(cycle)；vt,max(vt,min)为有轨电车平均行驶车速的最大(最小)值(m·s-1)；τij(j)为上(下)行有轨电车在交叉口Si与Si+1之间第j个站台的停靠时间(cycle)；Ni为交叉口Si与Si+1之间有轨电车停靠站数量。

图4 直行线路有轨电车绿波系统时空图Fig.4 Time-space diagram of straight tram line

直行有轨电车与干线上、下行左转社会车辆存在冲突。因此，与干线社会车辆绿波系统相比，直行有轨电车绿波的约束更为苛刻。有轨电车直行线路的绿波不能与上、下行红灯触碰，同时还要满足有轨电车较长的清空时间要求。图5为上行方向直行有轨电车绿波在4 种相位方案下受到的约束情况，其数学表达为

类似地，对于有轨电车下行方向，分析4 种典型相位方案，可以获得另一组约束条件为

根据有轨电车通行需求，设置有轨电车上、下行带宽约束范围为

货物丢失也是投诉中比例较大的。经常可以在一些报纸或新闻中看到快递公司丢失货物的消息，有的甚至连公司也不知道是在哪一个环节丢失的，这方面的投诉也越来越多。当前很多快递企业在对待用户的物品损坏或者丢失的投诉时，总喜欢以“能推就推，能拖就拖”的方式处理。前段时间身边的一个例子，快递公司说快递已经丢失，结果第二天又找到，还不肯送，造成这样的问题，还是自身素质存在缺陷。

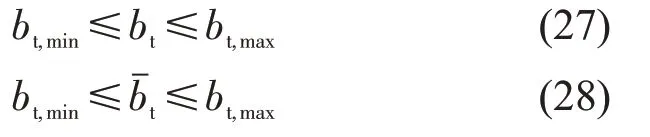
式中：bt()为直行线路有轨电车上(下)行绿波带宽(cycle)；tc,i()为上(下)行方向直行线路有轨电车在交叉口Si的清空时间(cycle)；bt,max(bt,min)为有轨电车绿波带宽的最大(最小)值(cycle)。

图5 wt,i 在不同相序相位组合下的约束Fig.5 Constraints for wt,i under various phase schemes

2.3 有轨电车左转线路约束条件

有轨电车左转线路中与直行线路共轨的部分，其相关约束条件与2.2 节直行线路的约束条件类似。

当上(下)行有轨电车在交叉口Sk左(右)转弯时，需要建立关于wtl,k和的特殊约束条件。如图6所示，当上行有轨电车左转通过交叉口Sk时，4种相位组合方案下的有轨电车左转线路约束可统一表示为

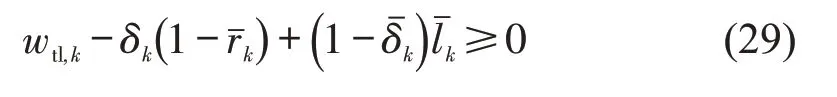
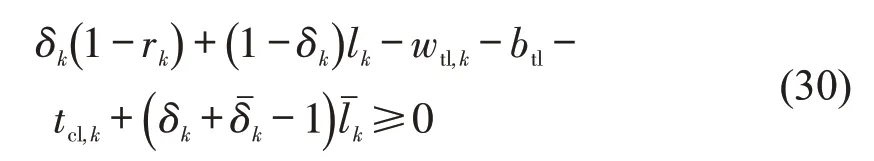
下行有轨电车右转通过交叉口Sk过程中，的约束分析与上行左转有轨电车方法类似，约束条件为

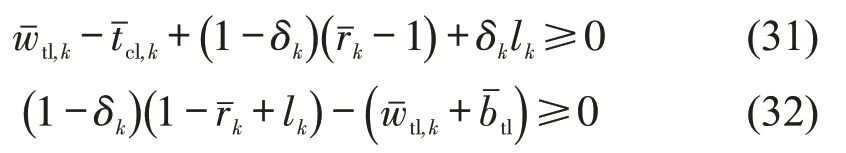
式中：tcl,k()为上(下)行有轨电车在第k个交叉口的左转清空时间；wtl,k()为上(下)行有轨电车左转绿波前锋与(下)行红灯时间右(左)侧的时间差。

图6 wtl,k 在不同相位组合下的约束Fig.6 Constraints for wtl,k under various phase schemes

2.4 社会车辆与有轨电车直左复线的交互约束条件

社会车辆的绿波系统和有轨电车直行、左转线路的绿波系统属于同一个信号协调控制系统。因此，各绿波系统相位差的差值必须是信号周期时长的整数倍，即符合

式中：mt,i()为整数变量。

2.5 模型目标函数设计

单个周期内至多有1列有轨电车到达交叉口，因而有轨电车绿波带宽满足基本通行需求即可。为提高整个干线系统的通行效率，以社会车辆绿波带宽最大为优化目标，构建目标函数为

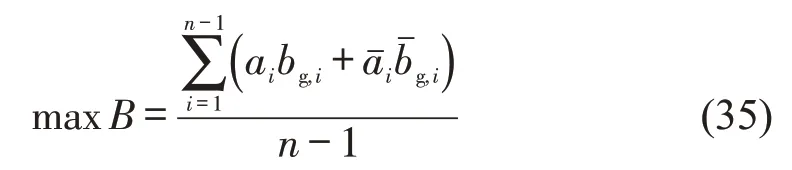
式中：B为所有路段社会车辆绿波带宽加权均值；ai和分别为交叉口Si与Si+1之间的上、下行方向路段的社会车辆绿波带宽的权重，可以用直行社会车流量与通行能力的比值表示。

以式(1)～式(34)为约束条件，式(35)为目标函数，构成一个混合整数非线性规划模型。模型得求解变量包括：通过分支定界算法或启发式算法可以获得该模型的最优解。

3 算例分析

以一条包括6个信号控制交叉口的干线为例，如图7所示。有轨电车轨道和站台都布设于路中，线路分为直行线路和左转线路，两条线路在第4个交叉口之前共轨，在第4个交叉口处分叉。

图7 有轨电车直左复线布局示意Fig.7 Layout of straight and left-turn tram lines

3.1 参数设置与输入变量

算例参数设置如表2和表3所示。模型优化过程中，交叉口绿信比固定，以保证通行能力稳定。有轨电车的最小带宽设置为10 s，满足基本通行需求。

表2 干线信号交叉口主要控制参数Table 2 Main parameters of phase schemes of intersections on arterial

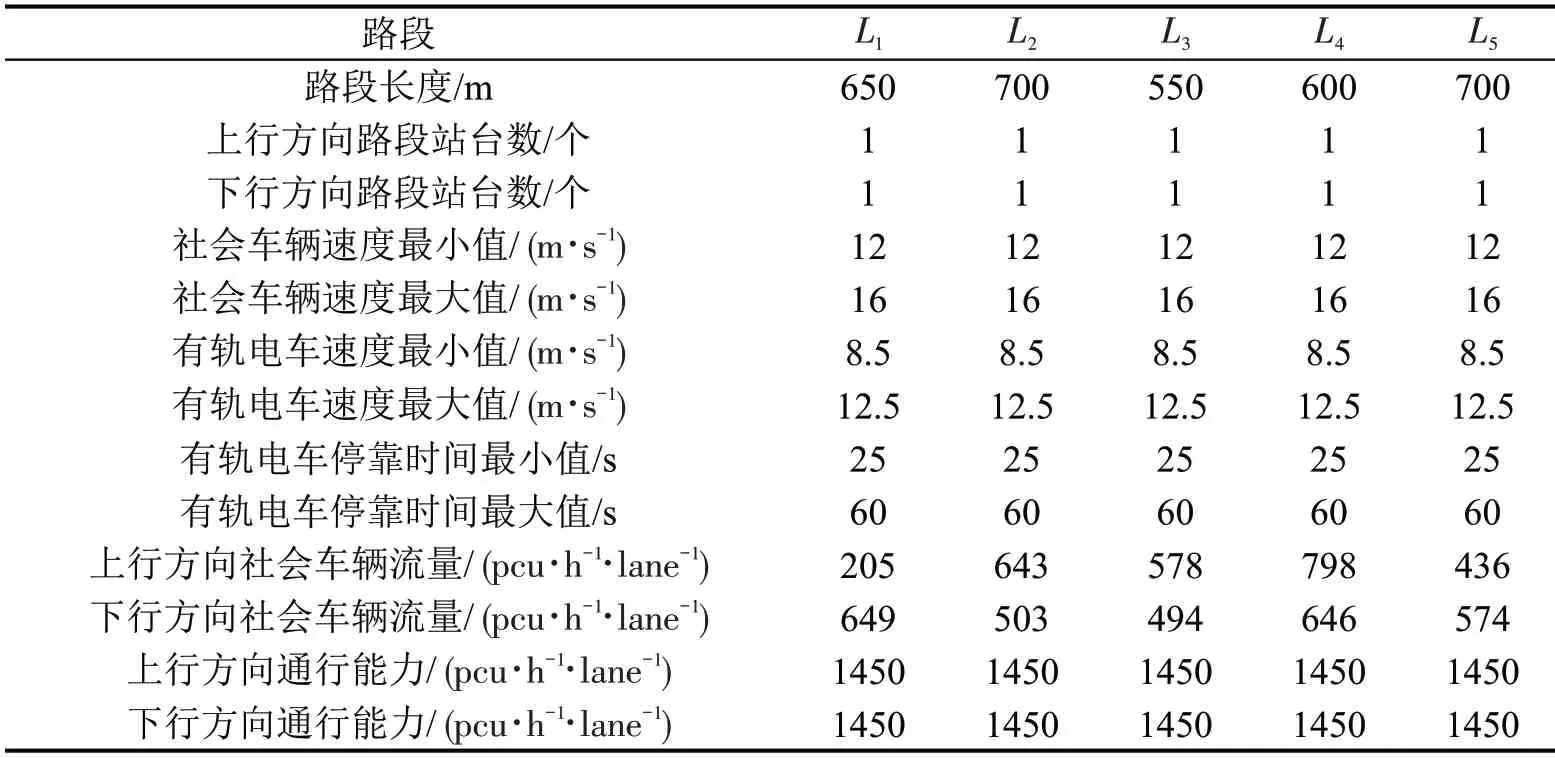
表3 干线主要交通参数Table 3 Main traffic parameters of arterial

3.2 结果分析

将案例中的参数和已知条件代入本文构建的混合整数非线性规划模型，应用数学规划优化器Gurobi求解模型，得到结果如表4所示。干线绿波整体信号周期长度为150 s，在保证有轨电车绿波带宽为10 s的基础上，获得社会车辆绿波带宽的最优解以及所有交叉口最优的相位方案。表5为每个交叉口的相位最优组合方式。社会车辆与有轨电车直行线路以及左转线路的绿波时空图如图8和图9所示。其中，粗实线表示的宽绿波为社会车辆绿波，细实线表示的窄绿波为有轨电车绿波。图9中，第4 个交叉口上行方向的点虚线表示上行方向左转相位时长。图中对有轨电车绿波轨迹进行了平滑处理，将停站等待时间包含在行程时间之内，因而绿波的斜率表示有轨电车在该路段的平均行程车速。

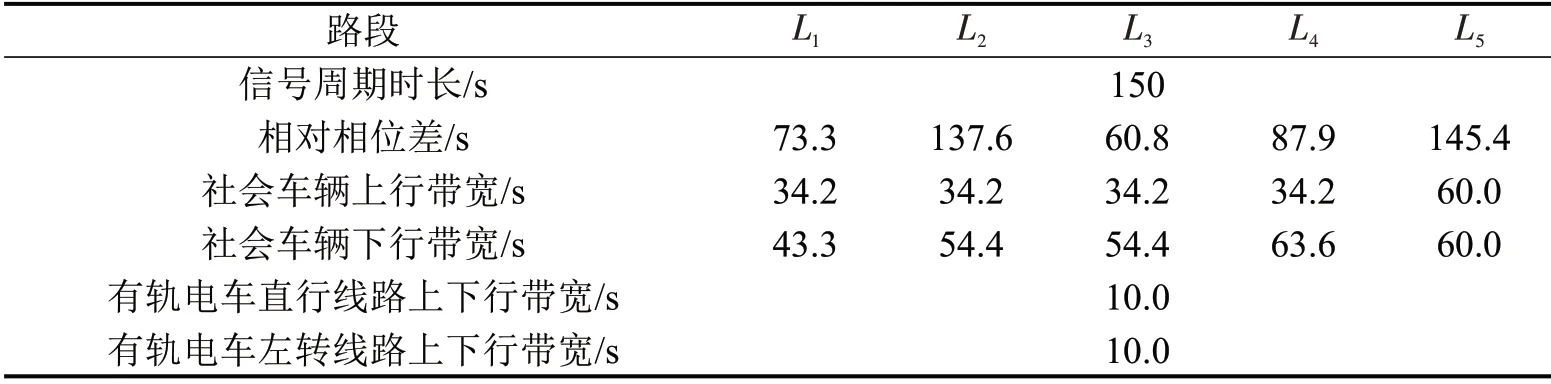
表4 模型优化结果Table 4 Optimization results

表5 沿线交叉口的δi 和优化结果Table 5 Optimization results of δi and for arterial intersections

表5 沿线交叉口的δi 和优化结果Table 5 Optimization results of δi and for arterial intersections

0-1变量δi δˉi S101 S210 S300 S401 S510 S600

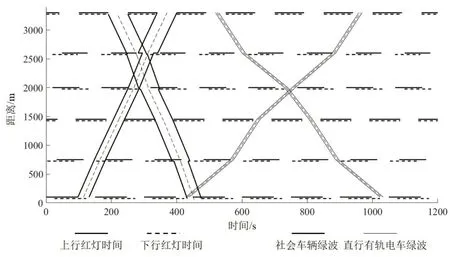
图8 直行有轨电车与社会车辆绿波时空图Fig.8 Time-space diagram of green waves for straight trams and general traffic

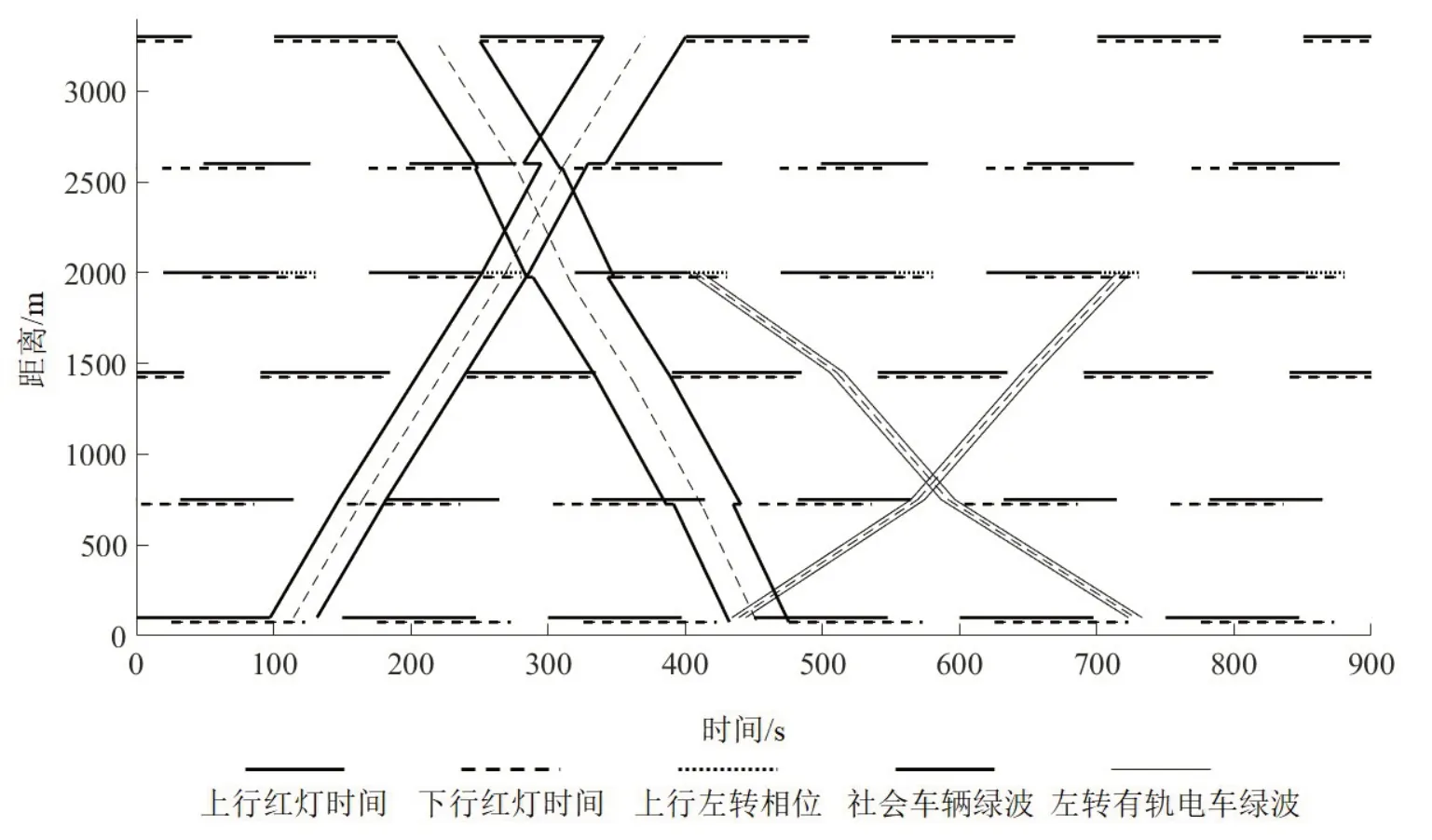
图9 左转有轨电车与社会车辆绿波时空图Fig.9 Time-space diagram of green waves for left-turn trams and general traffic

模型优化结果显示，社会车辆双向绿波带宽均不小于34 s，部分路段绿波带宽达到60 s 以上。直行与左转有轨电车的双向绿波带宽均为10 s。需要注意的是，本文绿波模型的约束条件为有轨电车安全通过交叉口提供了清空时间作为保障，该清空时间并不包括在有轨电车绿波带宽之内。因此，有轨电车仅需在绿波提供的10 s 时间窗口内达到交叉口前方即可确保安全通过交叉口。由于有轨电车行驶速度和停站时间具备较好的可控性，且通常一个信号周期内至多到达1列有轨电车，故有轨电车对绿波带宽的需求较小。

4 结论

本文得到主要结论如下：

(1)路中铺设轨道的交叉口，可采用早启迟断式控制，直行和左转有轨电车可分别利用社会车辆直行相位和左转相位通行。

(2)通过对MULTIBAND绿波模型中增加直行和左转有轨电车绿波约束条件，能够实现干线信号协调控制系统对社会车辆绿波、有轨电车直行和左转绿波的兼容，在满足有轨电车通行需求的前提下为社会车辆提供最大带宽绿波。算例表明，干线直左复线有轨电车可获得双向10 s通行带宽，社会车辆绿波双向带宽均大于34 s，部分路段绿波带宽可达60 s以上。

(3)本文为复线共轨式有轨电车干线的绿波方案设计提供了一般性方法论。模型中，有轨电车停站时间、交叉口清空时间、最小绿波带宽等参数均可根据实际情况进行调整。本文的优化方法同样适用于有轨电车的直右复线、左右复线，以及路侧式轨道布设情况。