山区公路隧道拱顶沉降回归模型的比选

魏弘铭， 范 瑛

(湖北工业大学土木建筑与环境学院， 湖北 武汉 430068)

山区公路隧道在其施工阶段中隧道拱顶沉降现象是一个多变复杂的非线性过程，对其变化量进行准确的预测与评估具有非常重要的工程意义。业界多采用半经验法、线性和非线性多元回归分析法对拱顶沉降监测数据建立多种模型，来分析预判新奥法施工的隧道拱顶产生的沉降值[1]。在隧道施工过程中，因环境复杂、监测仪器以及操作误差等多重因素的影响，常常会使得拱顶沉降监测数据不完全，因此单凭监测数据很难对拱顶沉降现象作出准确判断与评价。本文以山区公路隧道拱顶沉降监测数据为基础，建立变量，对数据进行处理，建立回归模型，研究分析监测数据存在的规律，具有科学、简便、实用性强的特点。具体做法是：依托竹山县西沟垭隧道工程，对监测数据进行处理，采用4种回归函数建立回归模型，通过显著性检验和回归曲线拟合对每一种回归模型进行比选，确定最适宜的回归模型，为西沟垭隧道拱顶沉降量分析预判提供科学依据，指导隧道施工。

1 工程概况

西沟垭隧道位于242国道竹山县上庸镇田家坝至峪口段改扩建工程的K4+025处，为新建单洞式隧道，隧道起止里程桩号为K3+765-K4+285，隧道全长520 m，最大埋深约102 m，建筑限界有效净高5.0 m，有效净宽10.0 m，净空断面面积为58.79 m2。勘察区域地貌单元属鄂西北构造侵蚀中高山区，山体起伏较大，地表植被较好，最大高程位于山顶，最低位置处于沟谷，相对高差约100 m，隧道区域山脊总体走向为北东西向，隧道轴线呈西北南向穿过山脊。西沟垭隧道从隧道进口处单向开挖，隧道施工按照新奥法原理，短台阶法作业。

2 显著性检验

2.1 相关系数

变量x和变量y之间是否存在线性关系，若存在线性关系那么线性关系程度的大小用相关系数r表示，即

相关系数r按三级标准划分：|r|<0.4为低度线性相关；0.4≤|r|<0.7为显著性相关；0.7≤|r|<1为高度线性相关[1]。

2.2 回归估计标准误差

通过回归模型得到的回归值与实际值之间偏离程度大小的指标用回归估计标准误差σ表示，即

σ值越小，回归值与其实际值的近似误差越小，回归值的代表性越强，用回归模型预测的结果越精确，回归模型的代表性越强[1]。

2.3 回归平方和U

回归平方和U表示，即

2.4 方差齐性检验

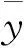
显著性水平α给定，本文选取α=0.05，计算F值，通过F值分布表比较。若F>F(1，n-2)，说明变量x与变量y有显著的线性关系，若F≤F(1，n-2)，则称变量x与y没有明显的线性关系，说明回归模型效果不显著，不具有代表性。

3 回归模型建立

回归模型就是基于已有的数据构建数学统计模型，得出变量之间关系的近似表达式，并根据表达式对相应的变量进行预测等[1]。

3.1 数据处理

选取测点稳定、无损坏、监测数据较完整的监测断面进行拱顶沉降回归模型的建立。西沟垭隧道拱顶监测断面布置较多，仅以桩号为K4+190的监测断面拱顶沉降数据为例，对回归模型的建立进行分析研究。在回归模型建立过程中，选择自变量为监测时间，拱顶累计沉降量为因变量。

回归模型的建立对奇异值非常敏感，奇异值的存在会极大地影响回归模型的效果以及后期拱顶沉降预测值，而在实际情况下，监测数据又容易受到多重因素影响而出现较大的波动起伏，因此在回归模型建立前，需对监测数据中的奇异值进行处理以提高回归模型的精度[3]。对于奇异值我们采用“拉依达准则”检验法找出剔除，并采用邻点中值法进行替换。

1)“拉依达准则”检验法

“拉依达准则”检验法又称为“3σ准则”检验法，对于一组数据{y1，y2，…，yi-1}，我们定义该组数据di：

di=2yi-(yi-1+yi+1)i=1,2,3,…,n-2

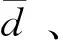
当qi>3时，则认为yi是奇异值[4]，应舍弃，空位值采用邻点中值代替。

2)邻点中值法

选择奇异值点两侧相邻点的数据yi-1和yi+1的中点值作为新的数据，新点yi计算公式为：

经过处理后的拱顶沉降数据如表1所示。

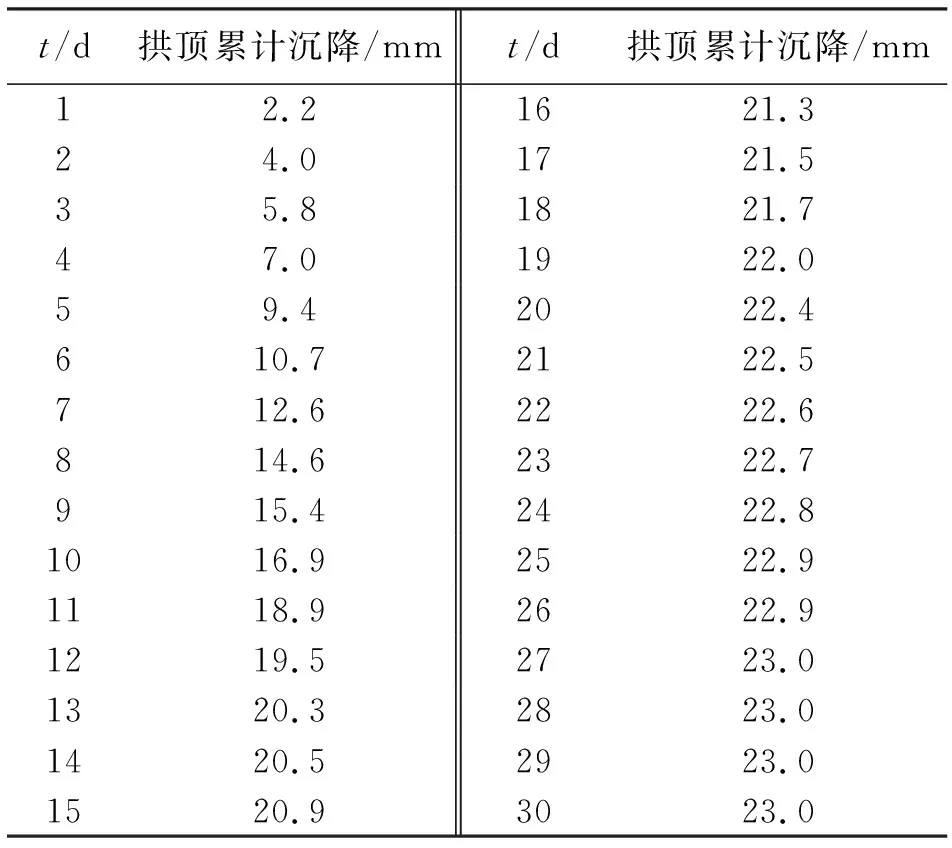
表1 隧道K4+190监测断面随时间变化拱顶累计沉降值

3.2 回归方程确定

根据JTGF60-2009《公路隧道施工技术规范》[5]的相关要求本文将分析下列4种回归函数模型的拟合效果：

幂函数模型

U=AtB

指数函数模型

U=Aexp(-B/t)

对数函数模型

U=A+Blg(1+t)

双曲线函数模型

U=t/A+Bt

式中：A，B为回归常数；U为拱顶累计沉降值,mm；t为初始沉降后的时间,d。

通过最小二乘法计算各回归模型参数，最小二乘估计法的思想就是对于每一个样本观察值(xi，yi)，使得观察值yi与f(xi)在该点处的误差平方和最小[6]。对于一元非线性函数模型，通过变量代换， 把一元非线性函数转换为一元线性函数y=a+bx，再利用最小二乘法计算参数a、b，通过a、b换算出曲线函数常数A、B值[7]。本文以指数函数模型U=Ae-B/t为例进行计算分析。

指数函数模型，表达式U=Ae-B/t，采用换元法，令y=lnU，a=lnA，b=B，x=-1/t，得转换函数:y=a+bx，对系数a、b采用最小二乘法算出，如下式所示：

(i=1,2,3,…,n=30)

(i=1,2,3,…,n=30)

求出回归方程表达式见下表，用同样的方法可得出幂函数模型、对数函数模型、双曲函数模型的回归方程表达式，计算过程见表2。

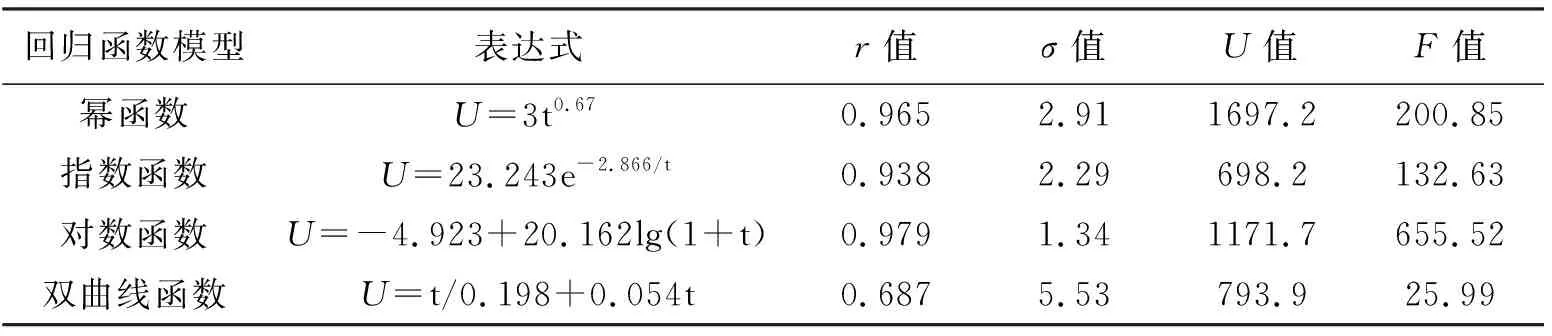
表2 回归函数模型表达式及相关参数统计表

4 回归模型的比选

4.1 回归曲线

回归曲线：两变量间呈现曲线关系的回归，确定两变量间数量变化的某种特定的规则或规律。各回归模型所对应的回归曲线与拱顶累计沉降量-时间实测曲线拟合图见图1～4。

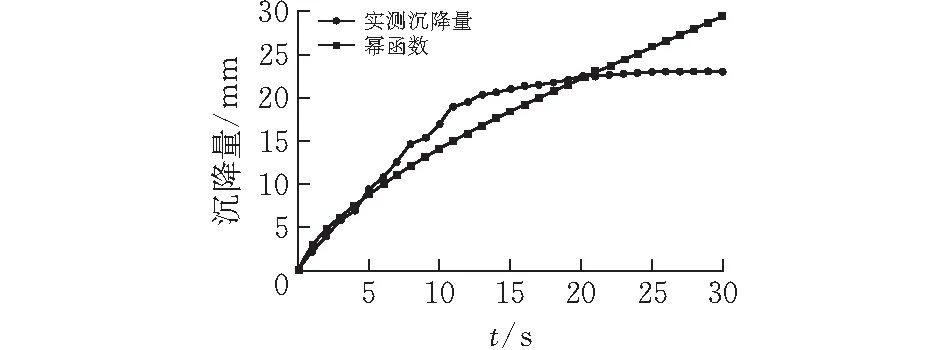
图 1 幂函数模型回归曲线

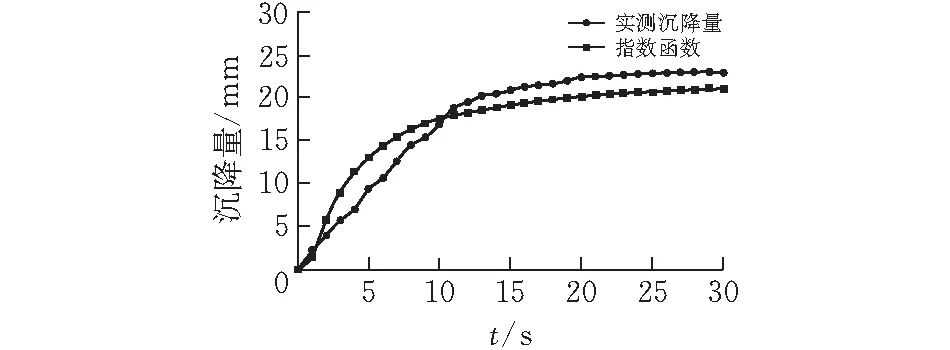
图 2 指数函数模型回归曲线

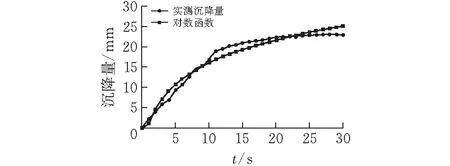
图 3 对数函数模型回归曲线

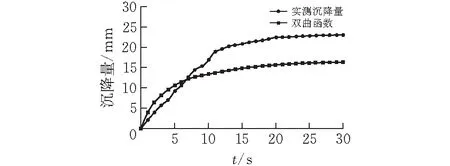
图 4 双曲线模型回归曲线

对比分析图1～4所示的回归曲线，对数函数模型是曲线拟合效果最好的，结合显著性检验中的相关系数r值、回归估计标准误差σ值、回归平方和U值、F检验值，在回归平方和U值比选方面，虽然幂函数模型U值大于对数函数模型U值，但综合各指标值以及回归曲线拟合趋势，显然对数函数模型能够更好地拟合实测数据，与实测数据相关度更高，所以最终确定对数函数模型为西沟垭隧道拱顶沉降评价分析模型，在后续西沟垭隧道施工过程中，采用对数函数模型，对拱顶沉降量进行预测分析评价以及合理确定二衬施作时间。

4.2 实测对比验证

通过显著性检验以及回归曲线拟合比选后得到的回归模型，在具体应用于实际分析前，要将回归模型与实际数据再一次对比验证，将t=18，19，…，26代入对数函数回归方程中，得出对应的拱顶沉降回归值，并与实际值进行对比，得到实际值与回归值对比表，见表3。

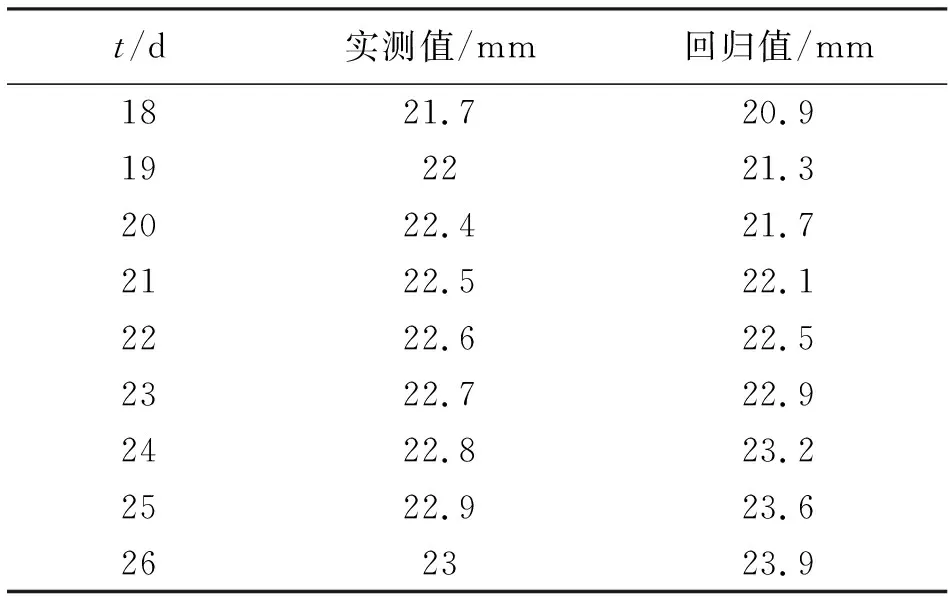
表3 实际值与回归值对比表

通过对数函数回归模型预测出隧道拱顶沉降在开始监测的第19 d后趋于基本稳定， 实测结果为第21 d以后趋于基本稳定，实测结果与预测结果基本对应，体现出回归模型分析结果的可靠性。回归相对偏差率=(回归值-实测值)/实测值，通过计算，回归相对偏差率在-0.03%～5.45%范围之间，偏差较小，对数函数模型得到的回归值与实测结果值吻合度较好，可以用于西沟垭隧道拱顶沉降现象的评价分析以及施工过程中沉降量的预测。

5 结论

1)利用4种回归函数对西沟垭隧道桩号为K4+190的监测断面进行拱顶沉降回归模型的比选，比选结果显示，4种回归函数模型中对数函数回归模型代表性最强，与实际情况吻合度更好，同时也表明各回归模型的适用性不同，应根据具体工程实际选择回归模型。

2)判断某一回归模型的优劣要从相关系数、回归差、回归平方和、F值、回归曲线与实测曲线拟合趋势等几个方面综合分析考虑，单一因素往往是片面的，不具代表性。

3)为了能够更好的分析评价隧道拱顶沉降现象，有些测点监测数据可能采用几种回归模型的组合，某一部分用一种回归模型，另一部分用另外一种回归模型，这样得到的结果可能更符合实际情况，这种组合模型在日后的运用过程中仍需深入分析探讨。