无界函数广义积分的一个注记*
2021-04-27 13:10:30刘新和郑顶伟陈占和
南宁师范大学学报(自然科学版) 2021年1期
刘新和,郑顶伟,陈占和
(广西大学 数学与信息科学学院,广西 南宁 530004)
下面引入奇点、奇线以及广义二重积分收敛性的定义。
设D为平面上的一个有界区域,点P0∈D。若f(x,y)在D{P0}上有定义,但在P0的任意的去心邻域内无界,则称P0为f(x,y)的奇点。设γ为D内含有P0的面积为0的闭曲线。若函数f(x,y)在Dγ有定义,但在任意包含曲线γ的区域上无界,则称γ为f(x,y)的奇线。




记Dε,δ={(x,y)|0≤x≤ε, 0≤y≤δ},则
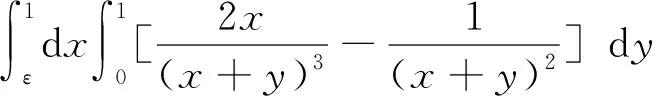
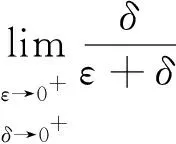
下面讨论2014年全国研究生入学考试数学(三)第12题及其参考答案。
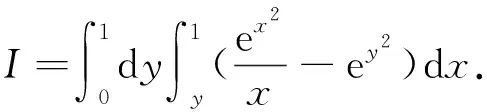
对任意的δ>0,令D1={(x,y)|0≤x<δ, 0≤y≤x},D2={(x,y)|δ≤y≤1,y≤x≤1},D3={(x,y)|δ≤x≤1,0≤y<δ},则o(0,0)∈D1且DD1=D2∪D3。

由积分第一中值定理可得

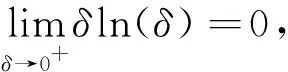

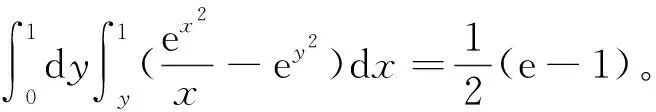

这是某高校高等数学期末考试中的一个考察二重积分的计算题,参考答案为:
由对称性可以得到
作为考察轮换对称性的期末考试试题,要避免出现奇点或奇线的问题。
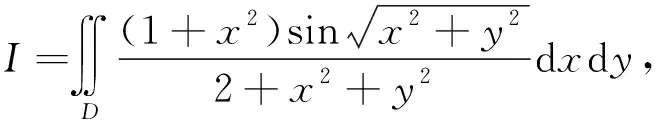
由轮换对称性可得
类似于定义1,可以把具有奇点、奇线的无界函数的广义二重积分的概念推广到具有奇点、奇线或奇面的无界函数的n(n≥3)重积分的情形。
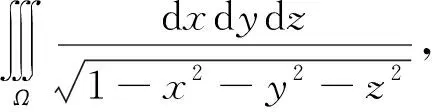
利用球面坐标变换x=rsinφcosθ,y=rsinφsinθ,z=rcosθ计算,这时Ω对应于Ω1={(r,φ,θ)|0≤r<1,0≤θ≤2π,0≤φ≤π}。因此,
猜你喜欢
中学生数理化·高二版(2024年2期)2024-06-17 17:49:31
车主之友(2022年6期)2023-01-30 07:58:18
新作文·小学低年级版(2022年6期)2022-08-30 03:01:42
小猕猴学习画刊(2022年12期)2022-02-06 03:00:58
小学生学习指导(爆笑校园)(2021年10期)2021-11-01 08:43:58
小学生学习指导(爆笑校园)(2021年9期)2021-09-27 03:45:38
小学生学习指导(爆笑校园)(2021年4期)2021-04-29 09:34:02
军事文摘(2020年14期)2020-12-17 06:27:46
上海建材(2020年5期)2020-12-15 00:33:32
数学物理学报(2016年6期)2016-04-16 04:41:05

