空调房间热环境实测与模拟

王洪利，徐鸿昌

(华北理工大学 冶金与能源学院，河北 唐山063210)

引言

2015年我国建筑面积总量约573亿m2，不断增长的建筑面积也带来了大量的建筑运行能耗需求[1]。建筑节能、绿色建筑等议题也日益受到重视。建筑能耗不仅与所采用的节能技术、节能措施有关，更受建筑的使用模式、室内环境需求水平的影响。在用户负荷变化较大的建筑中，集中式空调系统反而能耗更高、能效较低[2]。对于室内热环境和热舒适的研究，大多集中于采用集中空调的公共建筑，对于采用“部分时间、部分空间”的分体式空调制冷的住宅、办公房间的热环境研究较少。

校园办公室是一种较为典型的空调使用时间碎片化的房间类型，对于制冷需求的满足大多数是采用了后期加装分体式空调。房间空调安装较为随意，没有合理的气流组织优化，导致了舒适度欠佳。通过对实际空调房间的气流组织数值模拟，得到房间的热环境数据，并结合实地测量的热环境参数对比，验证数值模拟的正确性，最后综合分析了模拟房间的热环境。

1室内热环境实验与模拟

1.1 实验设置

热环境实测实验的房间，是位于本校的某一办公室。测量空调房间在空调器工作状态下，影响室内舒适度指数的几个客观指标的数据，具体包括温度、湿度和风速。

针对房间内的温度、湿度检测，选取4个工位测点布置传感器固定杆，分别在每个位置的0.1 m、1.1 m和1.7 m高度固定温湿度传感器，共12个测点。对制冷工况空调开启后室内温度趋于稳定，温度变化小于0.1 ℃的情况下的温度、湿度进行数据读取。同时选用一台热敏式风速仪，测量空调器风口的出风温度和风速，并且对各个测点的风速进行采集。4个工位测点平面位置关系如图1所示，实验器材及技术参数见表1。

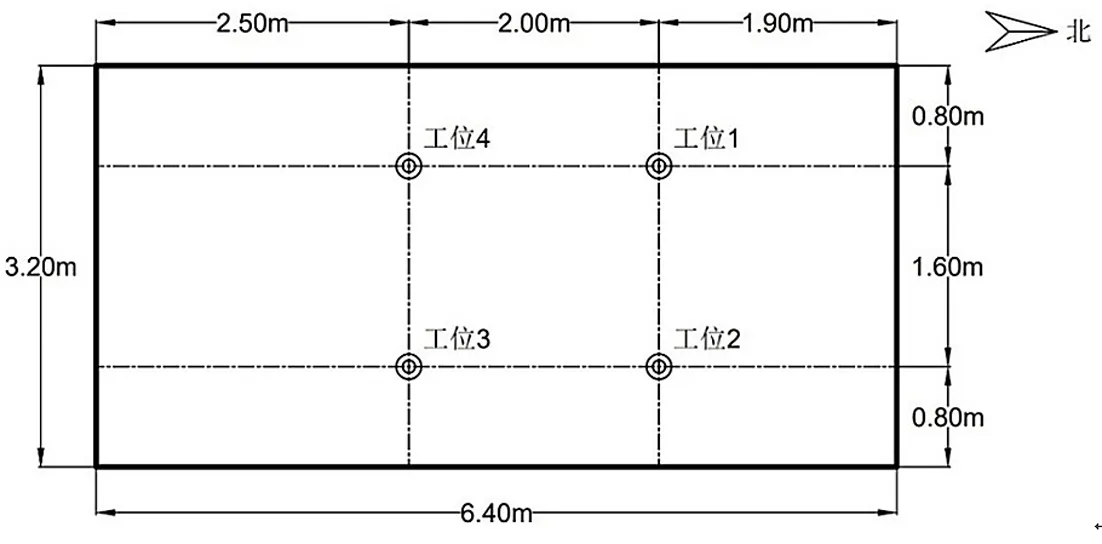
图1 房间工位测点示意图

表1 实验器材及技术参数

根据《GB50736民用建筑供暖通风与空气调节设计规范》，空调舒适度的设计参数如表2所示。实测空调参数的设置参照国家标准，综合考虑考虑夏季穿衣及节能因素，将空调温度设置为自动调节工况27 ℃。实测时室外气温35.8 ℃。

表2 人员长期逗留房间空调设计参数[3]

1.2 室内热环境数值模拟

1.2.1物理模型

房间选取为一典型单体办公室，房间长宽高为6.4 m×3.2 m×3 m，对应X轴、Z轴、Y轴，Z轴正向为北方向，X轴正向为东方向。房间西方向墙体上有一台分体式空调室内机，室内机尺寸870 mm(X)×280 mm(Y)×200 mm(Z)。送风口位于室内机下部，尺寸为600 mm×80 mm，回风口位于室内机顶部，尺寸为600 mm×100 mm。对外墙进行了简化，由于预期设置常热流边界条件，故省去了外窗，将外墙整体作为常热流的负荷源。东西两侧布置有两排长桌，有4名工作人员，4台电脑和4台显示器，具体参数见表3，详细分布见图2。

图2 房间物理模型

表3 设备列表及负荷设置

1.2.2边界条件

北侧墙体是与外界换热的外墙，设置为常热流边界，采用逐时计算法得到房间总热负荷，扣除设备及人员热负荷后，进而得到墙体传热负荷；其余墙体为内墙，相邻房间均为空调房间，可忽略彼此间换热。房间内其他设备和人员的设置参照表1。通过实际测量空调出风口风速并结合空气处理计算，出风口参数设置为风口风速3.2 m·s-1、出风温度15.8 ℃。

1.2.3网格划分

采用非结构化六面体网格，X、Y、Z方向网格最大单元尺寸为0.2 m，空隙间最少网格数量3个，模型每个边上的网格最少数量为2个。这样的设置可以对送风口、回风口等网格进行加密，保证计算精度。模型共划分网格单元145 169个，节点158 407个。风口处网格加密如图3所示。

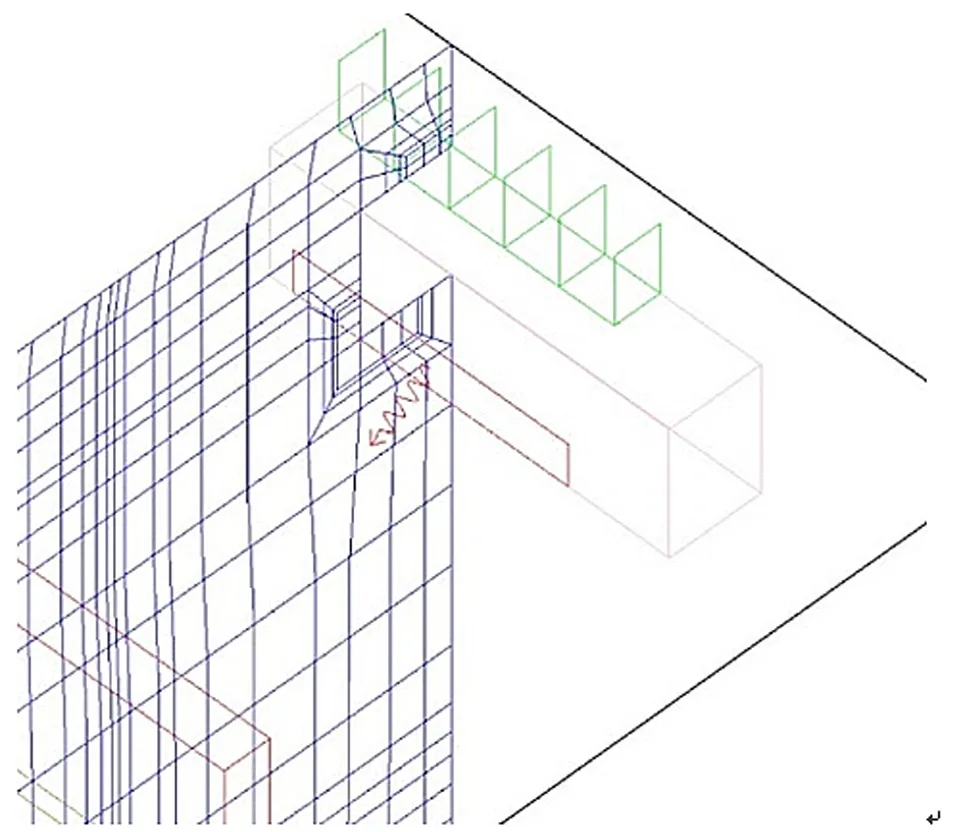
图3 局部网格加密

1.2.4 数学模型

为了对相应物理模型进行数值计算，该项研究对建立的数学模型进行适当简化，假设如下：

(1)室内的空气为理想气体，物性为不可压缩、密度是仅受温度影响的变量，且满足Boussinesq假设；

(2)办公室内空气流动为稳态湍流；

(3)室内空气为辐射透明介质；

(4)认为室内密闭性良好，不考虑漏风带来的扰动影响。

计算采用K-ε两方程湍流模型，控制方程见式(1)～式(8)。

模拟采用的控制方程由K方程、ε方程与动量方程、能量方程、连续性方程构成[4,5]：流体流动需满足质量守恒定律，即连续性方程：

(1)

式中：

ρ—气流密度，kg·m-3；t—时间，s；v为气流速度，m·s-1，下标i=1,2,3 表示X、Y、Z方向。

空气可以认为是不可压缩性气体，且空气的密度为常数值，因此上述连续性方程可以简化为下式：

(2)

流体也需满足能量守恒定律，表达为能量方程：

(3)

其中，k是分子运动所产生的导热系数，W·(m·K)-1；kt是因为湍流所导致的导热系数(kt=cpμt/Prt)，W·(m·K)-1；T是温度，K；ST是源项，W。

在一定时间内，流体微元体的动量变化大小等于这段时间内，作用在此微元体上的外力的综合。表达为动量方程(N-S方程)：

(4)

P为静压，Pa；x表示各轴方向，下标i、j=1、2、3分别表示X、Y、Z方向，且i≠j；τij为应力张量，Pa；ρgi为i方向因重力引起的体积力，N；Fi为其他源项，N。

K-ε两方程模型中，K为单位质量流量的湍流脉动动能，J。

(5)

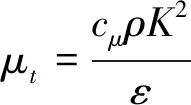
(6)

由以上定义，并结合N-S方程，可推得K方程和ε方程：

(7)

(8)

模型中各系数取值见表4。

表4 K-ε模型中的系数

1.2.5计算及收敛条件

速度与压力耦合采用SIMPLE算法。收敛条件为：流动方程(动量与连续性方程)、K方程、ε方程相对误差1×10-3，能量方程相对误差 1×10-6。

2结果对比与分析

2.1 温度

人体能够最直观感觉的房间热环境是温度的高低，垂直高度上的温差更是人体热感觉影响较为突出的因素。依据ISO7730国际标准，0.1 m和1.1 m高度垂直高度温差分为A、B、C3个等级，分别要求温差小于2 ℃、3 ℃和4 ℃[6]。美国ASHRAE55标准建议，坐姿状态下，地面上方0.1 m和1.1 m之间的温差≤3 ℃；站姿状态下，地面上方0.1 m和1.7 m之间的温差≤4 ℃[7]。

图4中数据为实测与模拟温度值。各点温度值均能够满足GB50736对室内温度的基本要求。模拟所得各个测点的温度值相比实测值整体趋势较为一致，数值上略有偏差，除2号工位的2个测点，其余都呈现处温度下低上高的分布。各个工位的垂直温差最大值为1.7 ℃，小于2个标准的建议值，满足垂直高度上的温差要求。

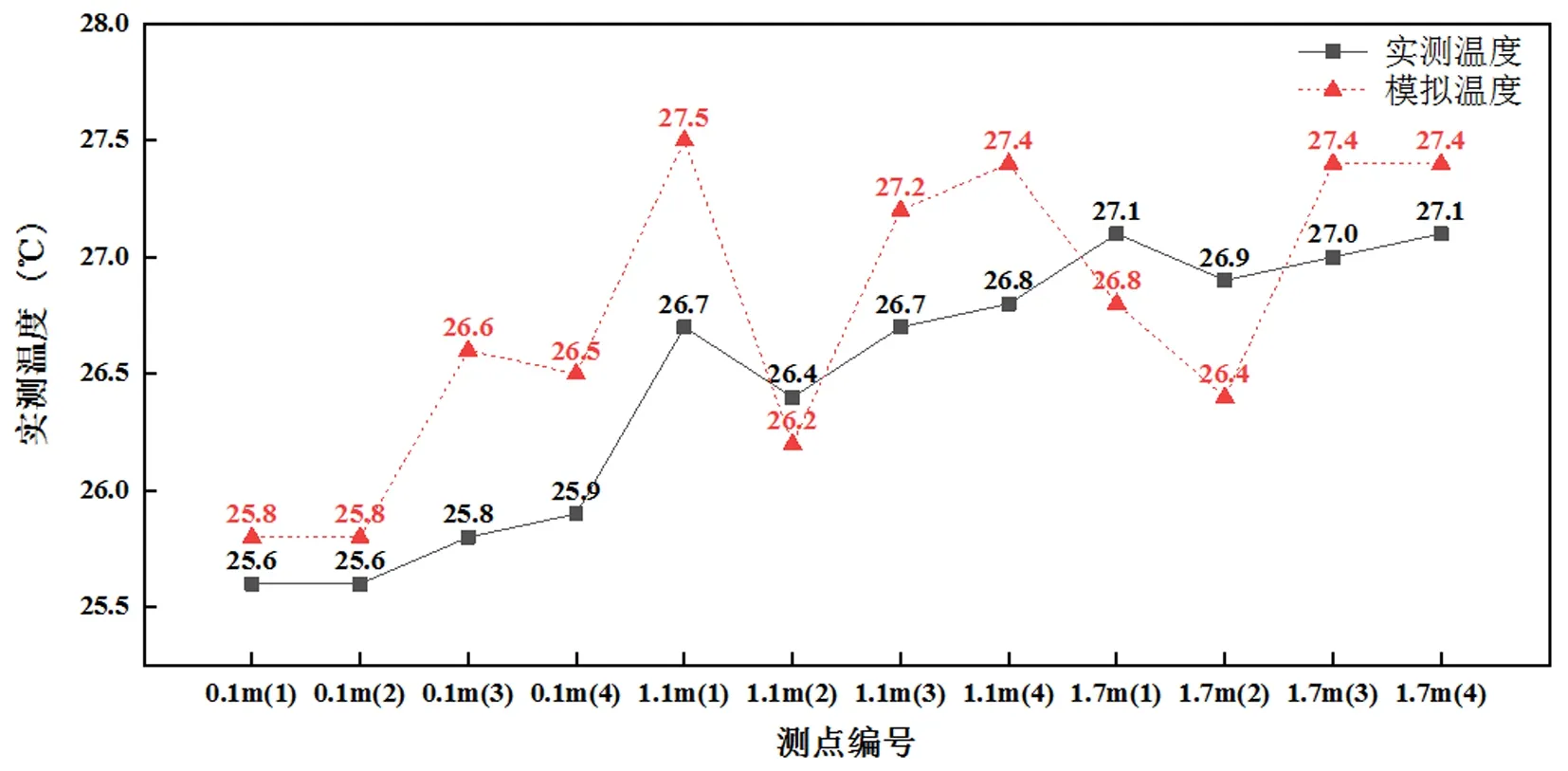
图4 实测与模拟温度值

图5为模拟所得的各高度截面的温度分布云图。由图5可知，各个高度截面的大部分面积的温度分布较为均匀，但是都会在空调出风口一侧出现或多或少的冷区。在0.1 m和1.1 m截面上，冷区有一定程度的扩散，面积较大，但是温差相对和缓；在1.7 m截面上看到的冷区分布较为集中，但是温差十分明显。各截面的温度平均值由0.1 m至1.7 m分别为26.5 ℃、27.0 ℃和26.9 ℃。水平高度上的温度梯度也大致呈下低上高的分布，与实测所得到的趋势较为一致。

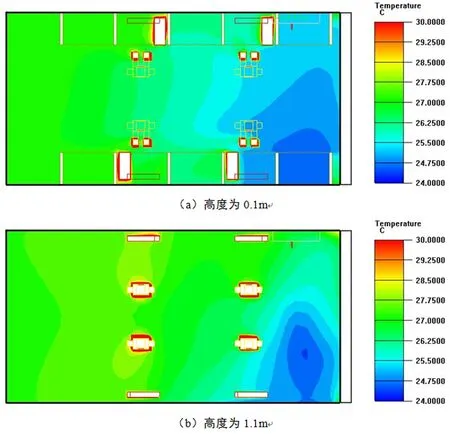
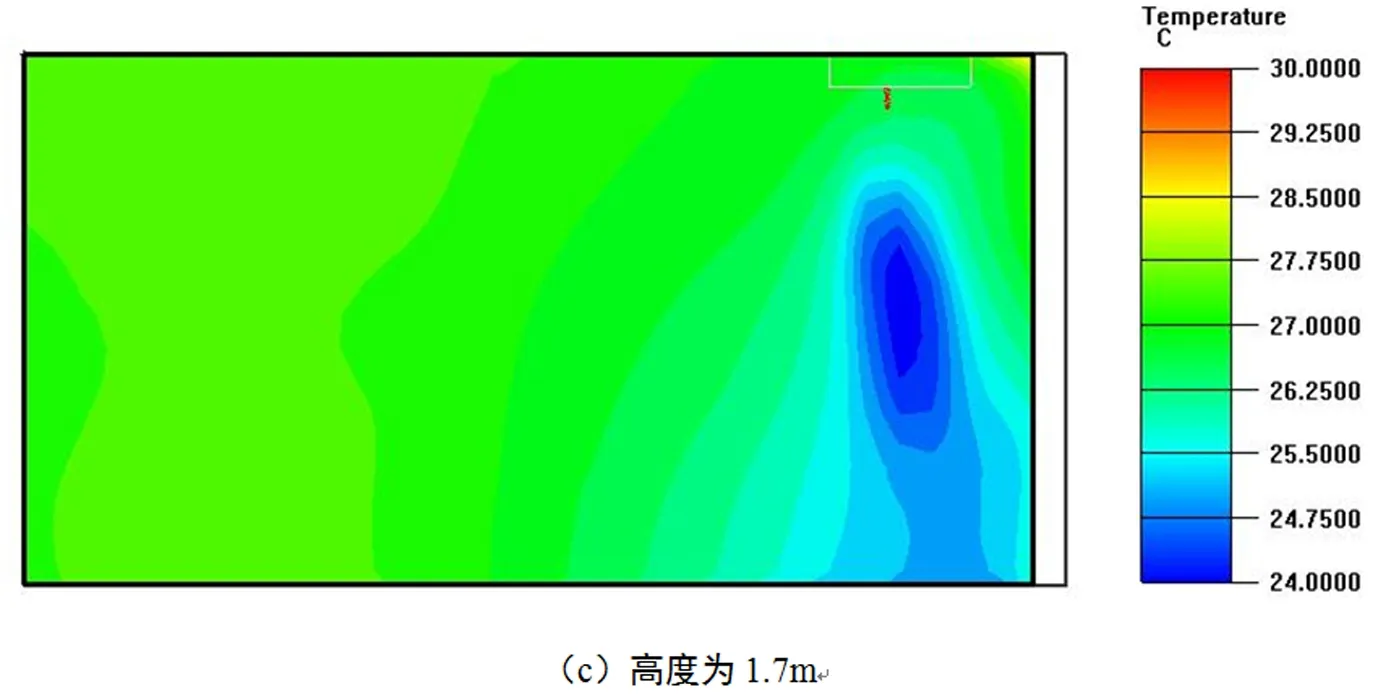
图5 各高度温度分布

2.2 风速

图6为实测与模拟温度值数据，图7为各高度速度分布云图。

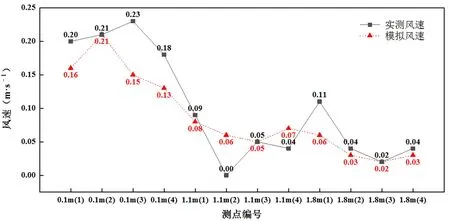
图6 实测与模拟温度值

图7 各高度风速分布

由图6可知，模拟所得各测点风速值与实际测量具有很好的趋势一致性，风速值在高度方向上呈现下高上低的整体趋势，底层的气流相对上层比较活跃。数值上风速整体都小于0.3 m/s，满足《GB50736民用建筑供暖通风与空气调节设计规范》中的要求。从图7速度分布云图上来看，0.1 m高度整体的气流活跃度高于其他2个截面，而1.1 m和1.7 m截面上整体的气体流动不明显，但是出现了局部的高风速区。1.1 m的局部风速超过了0.3 m/s，高速区中心部分可达到0.5 m/s以上；1.7 m局部风速超过了0.5 m/s，高速区中心风速可达0.89 m/s。

数值上，0.1 m、1.1 m和1.7 m高度的风速平均值分别为0.087 4 m/s、0.067 4 m/s和0.084 5 m/s。如果剔除局部高风速对平均值的影响，那么风速在垂直高度上也是呈下高上低的分布，与测点所得趋势是一致的。

2.3 湿度

根据徐昆仑的研究[8]，夏季相对湿度在30%～50%之间的可接受温度范围在23.8～28.9 ℃。图8所示为12个测点数据在温度、湿度图上的分布，实测各测点温度为25.6～27.1 ℃，相对湿度为49.1%～45.6%，二者综合后的数据点都落在了满足舒适度的范围之内。

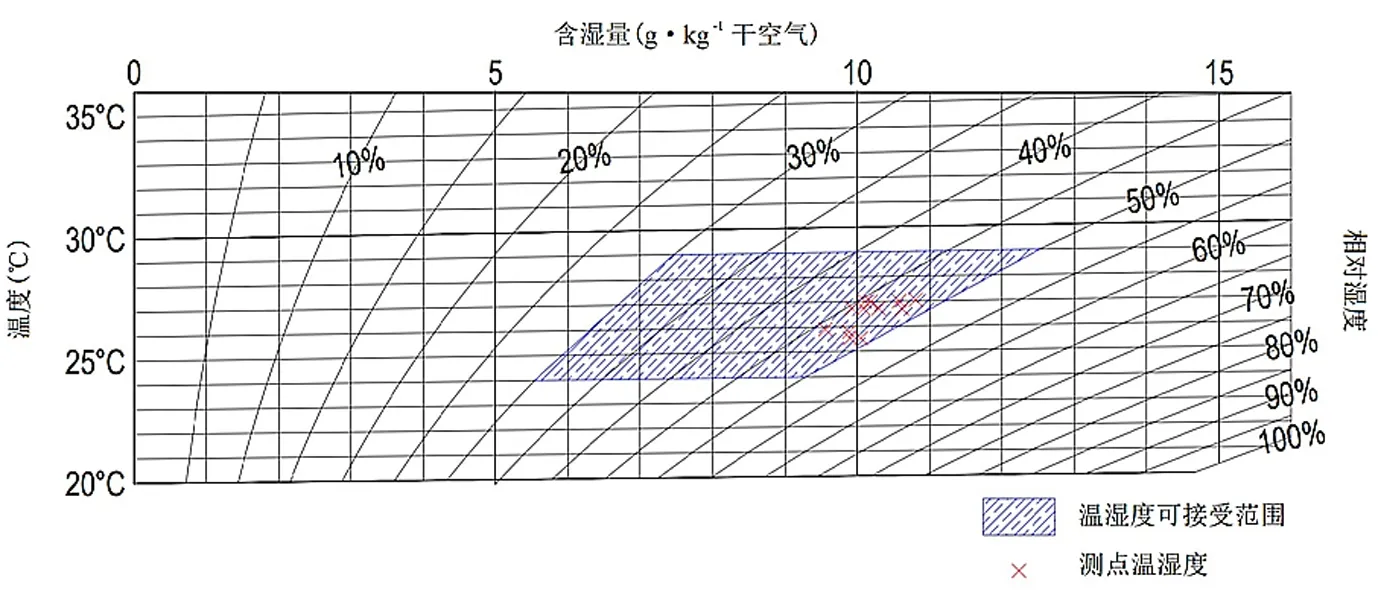
图8 各测点数值在温湿度图上的分布

图9所示为实测的室内相对湿度与含湿量，12个测点的值相差不大，相对湿度平均值为47%，满足《GB50736民用建筑供暖通风与空气调节设计规范》中对夏季空调舒适度的要求；结合温度将相对湿度转换为空气含湿量后，各点的数值差距也不明显，围绕10 g/kg干空气浮动，平均值为10.1 g·kg-1干空气。2个参数说明室内的湿度分布情况较为均匀，多点平均湿度值可以代表室内整体的湿度。

图9 各测点相对湿度及含湿量

3结论

(1)数值模拟采用了将模型部分简化、冷负荷设置为常热流边界的方法，经过实测数据与模拟结果的数据进行对比，验证了该模型的可靠性。

(2)相对湿度的实测结果显示出了实际室内环境在稳定的条件下，各个区域的相对湿度小幅度变化，同时实际空气的含湿量不会有很大的变化，整体室内的湿度分布均匀稳定。

(3)由实测和模拟所得热环境数据可知，对于温度、垂直温差、风速和湿度几个参数，房间内大部分人员活动区域都可以满足各项标准的要求。

(4)房间仍然存在不小的低温区和高风速区，这会导致室内人员的不舒适感，室内空调的风口形式和布置位置仍有优化空间。