采用不同模型预测低碳Fe–Ni 合金等离子熔覆层的冲击韧性

胡明强，胡永俊，李蓝特，邹小风，李风，舒畅

（广东工业大学材料与能源学院，广东 广州 510006）

等离子熔覆伴随着许多非常复杂的物理、化学变化，如熔化、凝固、固态相变、热辐射、热对流等。不同的工艺参数，比如喷头移动速率、熔覆电流、离子气流量等都会对工件产生影响，并且有些工艺参数的影响较大。若要获得较好的工艺参数，需要进行大量的重复性试验，阻碍了等离子熔覆的快速发展。

在数据处理方面，应用广泛的神经网络是一种通过BP(误差反向传播)算法训练的多层前馈网络，是快速实现流程优化的方法之一。通过不断的训练与学习，它可以自动建立输入与输出之间的映射关系，非常适用于阐述等离子熔覆工艺参数与涂层性能之间的非线性关系。周建忠等[1]针对BP 算法中存在的收敛速率慢、全局搜索能力弱等问题进行优化，设计了进化神经网络学习算法，从而建立了激光熔覆的BP神经网络。该算法的预测结果与试验结果误差不大于2.14%。杨友文等[2]基于熔覆层形貌质量、激光功率、扫描速率等也建立了BP 神经网络，预测值与实测值的误差不大于4.6%。彭竹琴等[3]利用反馈式神经网络预测硼铸铁等离子熔凝层的硬度，预测值与试验值的误差小于4.3%。

本文在高锰钢表面通过等离子熔覆制得低碳Fe-Ni 合金涂层，并采用不同模型来预测熔覆工艺参数对涂层冲击韧性的影响，为等离子熔覆层的制备提供理论指导。

1 实验

1. 1 材料

基材为块状Mn13 钢(Si 0.30% ～ 1.00%，Mn 11.00% ～ 14.00%，C 1.10% ～ 1.40%，P≤0.07%，S≤0.05%，Fe 余量)，尺寸为55 cm × 10 cm × 5 cm，经过水韧处理后通过砂轮机打磨至光亮，再用丙酮溶液或酒精洗涤，最后用吹风机烘干。通过雾化法得到本文所用粉末(Ni 18.25%，Co 9.10%，Mo 4.93%，Si 3.00% ～4.00%，Mn≤0.10%，C≤0.03%，Fe 余量)，在熔融状态的18Ni(300)马氏体时效钢中额外加入3% ～ 4%的硅粉以提高粉末的流动性，再采用高压气体将它们直接破碎为细小的液滴，然后快速冷凝成粉末，粒径均在45 ～ 110 μm 范围内。

1. 2 试样的制备

为了建立数据库，首先在不同工艺参数下制备熔覆层。选取3 个影响较大的因素设计了如表1 所示的试验，其他参数为：喷距8 mm，进料气流量2.5 L/min，重叠率30%。将粉末装入德国制造的Castolin Eutectic 等离子熔覆机，固定基体，设置好工艺参数后打开送粉开关，喷头移动到预设位置，同步送粉，在基体上沿S 形轨迹，熔覆平行的6 ～ 7 道涂层。

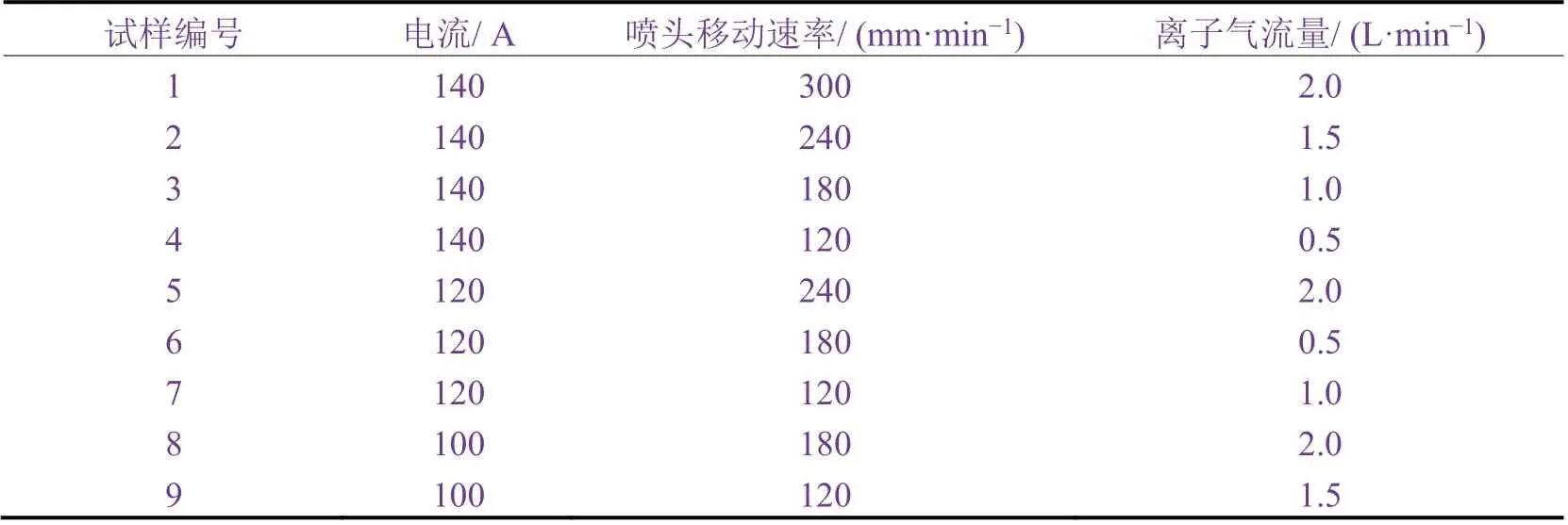
表1 不同操作参数下等离子熔覆试验Table 1 Plasma cladding experiments under different operation conditions

等离子熔覆中心温度约为3 000 °C，而基体温度为室温，温差极大，极易由于热应力而产生热裂纹，因此第一道只预热基体，不参与后续检测。熔覆完成后，将线切割好的试样放入热处理炉中进行固溶，随炉升温，达到820 °C 后保温1 h，再放入水中冷却至室温。在固溶时要分开摆放，否则在淬火时有可能改变试样尺寸。水冷后再进行时效处理，即将固溶后的试样分别放置在300、400、500 和600 °C 的热处理炉中保温5 h，随后空冷。加上不进行时效，总计45 组试验，以它们的结果作为神经网络数据库。

1. 3 冲击韧性的测试

利用砂纸和金刚石抛光膏对试样进行打磨，以去除表面污渍。采用JB-S300 数显式摆锤击试验机测试冲击韧性。将试样摆放到冲击口，V 形缺口背向摆锤一侧，选用冲击能量为150 J 的小锤作为冲击锤。

1. 4 实验原理

线性回归模型先假设预测值与特征值之间存在单调性，再构建如式(1)所示的损失函数。

损失函数求解，得到线性回归方程(2)。

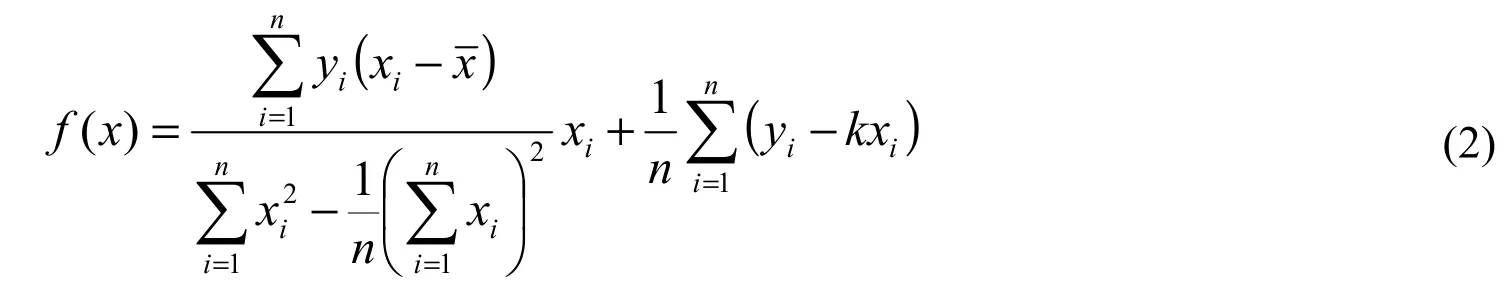
BP 神经网络一共有3 层结构，分别是输入层、隐含层和输出层，神经元组成为4-10-1。通过Python语言编程，设置a、b、c、d四个可输入参量，分别为等离子熔覆电流、喷头移动速率、离子气流量及热处理温度。将冲击韧性作为输出。神经网络的拓扑结构如图1 所示。

鉴于BP 网络在训练过程中容易陷入局部最小误差函数值，导致网络的预测精度较低[4]，于是引入粒子群算法(PSO)进行优化[5-11]，简化过后的学习过程如图2 所示。

在PSO-BP 模型中，粒子都被赋予一个适应度值，每个粒子都有一个速度v来确定其方向和距离。算法迭代之后最优解的单粒子被称为个体极值，而最优解决方案获得的粒子群被称为全局极值。算法的基本特征表达式如式(3)和式(4)。

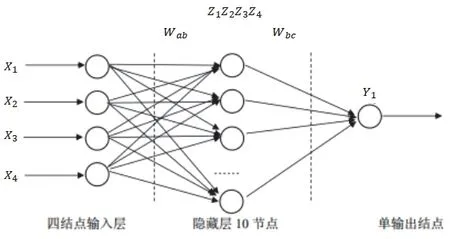
图1 BP 神经网络拓扑结构Figure 1 Topological structure of BP neural network

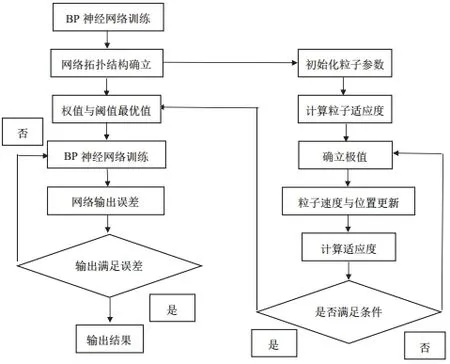
图2 PSO-BP 模型学习流程Figure 2 Learning process of PSO-BP model

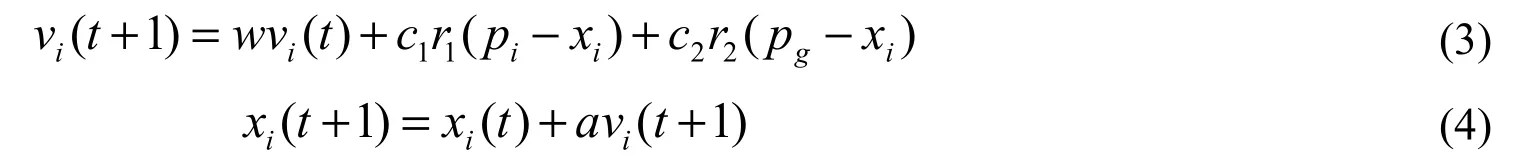
随机设定粒子的初始值，种群范围由BP 模型的数据设定。如图3 所示，在搜索全局最优解时，适应度会不断降低，直至最低值，冲击韧性在迭代76 次后收敛于0.037。

图3 适应度随迭代次数的变化曲线Figure 3 Variation curve of fitness value of the model with the number of iterations

惯性因子w由Shi 提出的惯性因子线性递减法(LDW)[12]计算所得，如式(5)所示。

学习因子c1、c2和种群规模由经验设定。根据迭代算法[13]更新速度v和粒子x。再采用粒子群算法全局搜索BP 网络预测的最优适应度，得到对应的粒子。以粒子本身作为新BP 网络的初始参数，即权值和阈值。

PSO-BP 模型的参数设定如下：种群规模20，种群设置为[-5,5]，迭代次数100，惯性因子w0= 0.9，wt= 0.4，学习因子c1=c2= 1.5。

2 结果与讨论

2. 1 热处理温度对冲击韧性的影响

采用日本制造的Smartlab 9kW 高分辨X 衍射仪(XRD)确定1 号试样分别进行不同热处理后所得熔覆层表面的相组成。从图4 可知，未进行时效的涂层的相组成主要为α-Fe，以及一定数量的Co3Fe7和铁镍化合物。300 °C 时效后出现少量CoFe，涂层组织因此得到强化。400 °C 时效后还出现Ni3Mo 和Mo0.25Ni0.75，这两种钼镍化合物以第二相颗粒的形式存在于晶界中，对涂层组织具有很大的强化作用。相比300 °C 时效，400 °C 时效后析出强化相的种类和数量都有所增多。500 °C 时效后涂层的主要相组成相比于400 °C 时效，多了Ni3Ti 这种新化合相，而且Ni3Mo 相的衍射峰强度有所增加。600 °C 时效后相成分发生明显变化，Ni3Mo 有所减少，Ni3Ti 这种强化相消失，此外多了Fe2Mo 这种新相，这是温度过高所致。

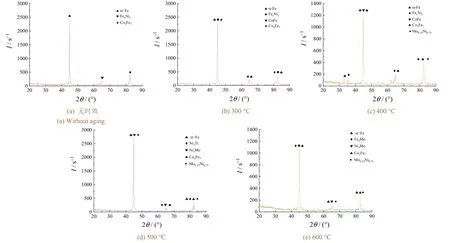
图4 经过不同温度时效后熔覆层的XRD 图谱Figure 4 XRD patterns of claddings after being aged at different temperatures

从图5 可见，温度对与冲击韧性有一定的影响，冲击韧性随着热处理温度升高而上升，这主要是因为金属间化合物颗粒(如Co3Fe7、Fe0.64Ni0.36、Mo0.25Ni0.75)随着温度升高而析出。温度超过500 °C 韧性略微下降，主要由于金属间化合物颗粒逐渐溶解且晶粒也开始变粗[14-15]。

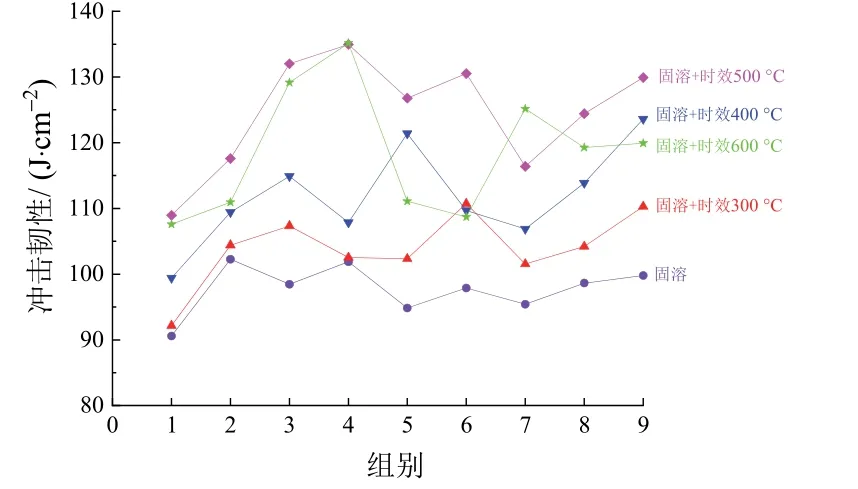
图5 不同条件下所制熔覆层的冲击韧性Figure 5 Impact toughness of coatings clad under different conditions

2. 2 线性回归模型

由于冲击韧性随着时效温度升高而升高，在预测冲击韧性时，线性回归模型稍微准确。从表2 可知，冲击韧度与时效的线性关系较为明显，相对误差也偏小。经过线性回归方程多次模拟的相对误差均值为7.06%。但是由于数据集未进行降噪处理，在多次模拟时会出现误差突然增大的现象，而且线性回归模型仅适用于具有线性关系的模型，存在一定的局限性[16]。

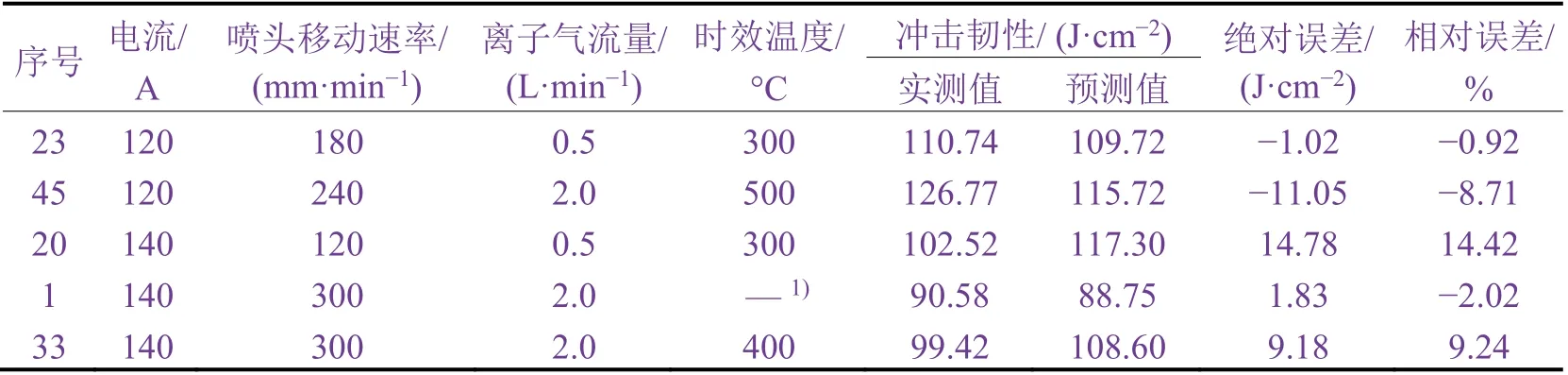
表2 冲击韧性的实测值与采用线性回归得到的预测值Table 2 Measured impact toughness in some experimental groups and corresponding values predicted by linear regression

2. 3 BP 模型

为了防止模型因为不一定具有线性关系而产生误差，更具普遍性，进一步采用BP 神经网络来进行模拟预测。从45 组数据中随机抽取5 组用于验证，剩余40 组用于训练模型。从表3 可知，经过多次模拟后得到的BP 模型的相对误差平均值为6.12%。但明显能看出BP 神经网络具有偶然性，由于权值与阈值不稳定，相对误差陡然增大一次。因为用于模拟的数据不够充足，BP 神经网络的权值和阈值没有得到很好的优化，所以该模型还不成熟，不能用于实际试验预测中。

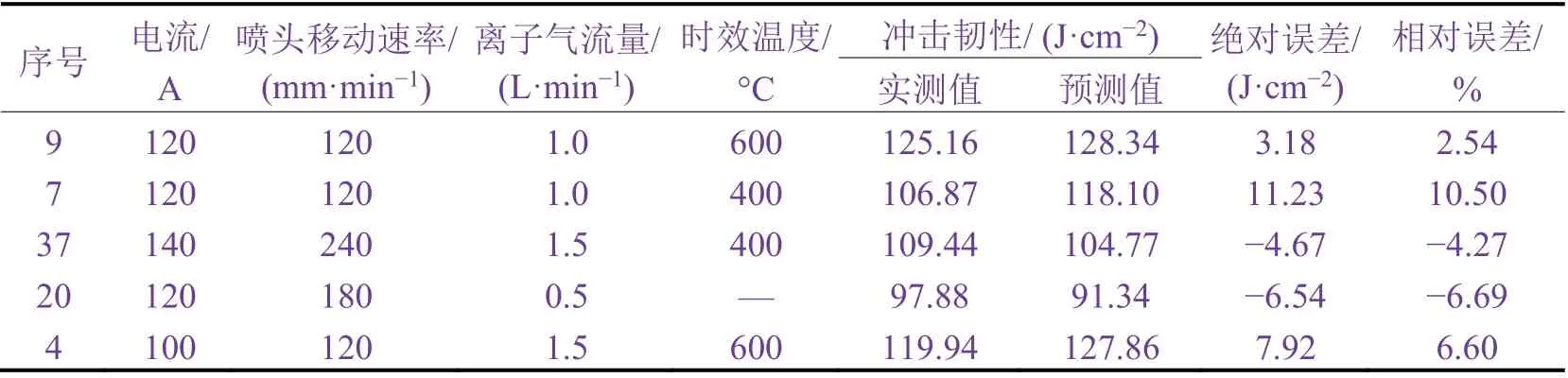
表3 冲击韧性的实测值与采用BP 模型得到的预测值Table 3 Measured impact toughness in some experimental groups and corresponding values predicted by BP model

2. 4 PSO-BP 模型

为了解决由于缺少大量数据而无法得到良好优化的BP 模型的问题，通过引入粒子群算法对BP 模型进行优化，以稳定其权值和阈值。从表4 可知，PSO-BP 模型的预测值与试验数据较为接近，经过多次模拟后的相对误差的均值为3.03%。

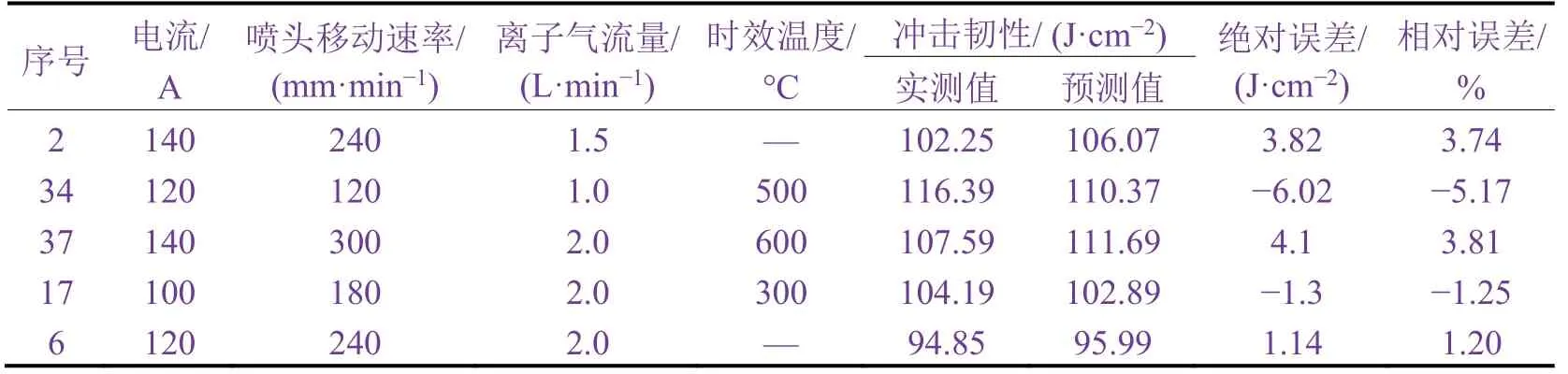
表4 冲击韧性的实测值与采用PSO-BP 模型得到的预测值Table 4 Measured impact toughness in some experimental groups and corresponding values predicted by PSO-BP model

2. 5 不同模型的比较

从表5 可知，线性回归模型适用于预测具有线性关系的数据，BP 神经网络模型适用于经过大量数据训练后的试验预测，PSO-BP 模型的预测效果较好，可以为实际生产和研发提供较好的非实验数据。

3 结论

通过调整工艺参数在高锰钢表面获得了低碳Fe-Ni 合金涂层，并用3 种模型对所制熔覆层的冲击韧性进行预测。结果表明：本文涉及的非线性问题不能用线性回归模型来解决；BP 神经网络在缺少大量训练数据的条件下精确度不足；引入粒子群算法后构建的PSO-BP 模型的预测最为准确。

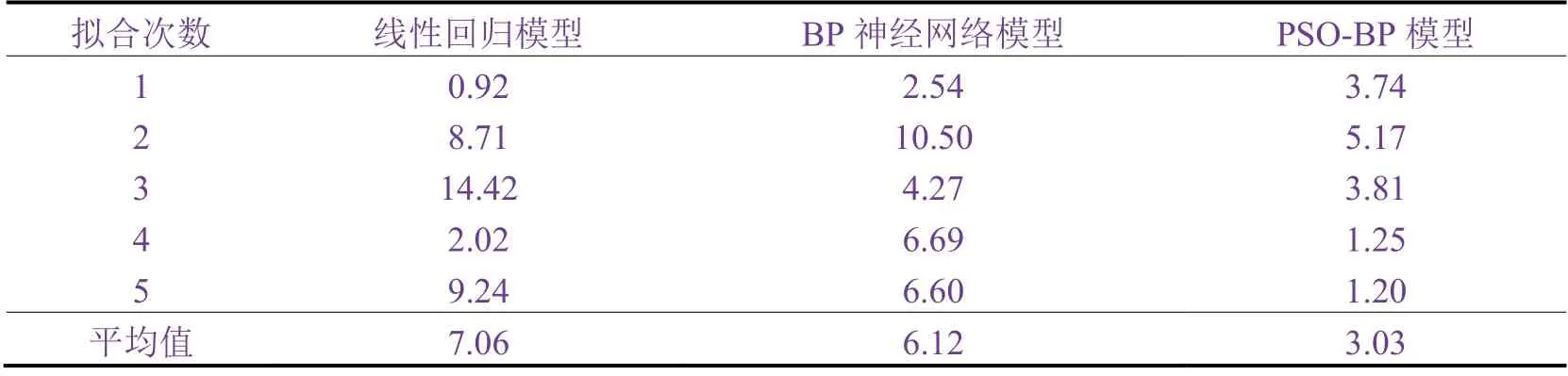
表5 3 种模型的相对误差Table 5 Relative errors of three models（单位：%）