MHD Maxwell Fluid with Heat Transfer Analysis under Ramp Velocity and Ramp Temperature Subject to Non-Integer Differentiable Operators

Thabet Abdeljawad,Muhammad Bilal Riaz,Syed Tauseef Saeedand Nazish Iftikhar

1Department of Mathematics and General Sciences,Prince Sultan University,Riyadh,12435,Saudi Arabia

2Department of Medical Research,China Medical University,Taichung,404,Taiwan

3Department of Computer Science and Information Engineering,Asia University,Taichung,41354,Taiwan

4Department of Mathematics,University of Management and Technology,Lahore,54770,Pakistan

5Institute for Groundwater Studies(IGS),University of the Free State,Bloemfontein,9301,South Africa

6Department of Science&Humanities,National University of Computer and Emerging Sciences,Lahore,54000,Pakistan

ABSTRACT The main focus of this study is to investigate the impact of heat generation/absorption with ramp velocity and ramp temperature on magnetohydrodynamic (MHD) time-dependent Maxwell fluid over an unbounded plate embedded in a permeable medium.Non-dimensional parameters along with Laplace transformation and inversion algorithms are used to find the solution of shear stress,energy,and velocity profile.Recently,new fractional differential operators are used to define ramped temperature and ramped velocity.The obtained analytical solutions are plotted for different values of emerging parameters.Fractional time derivatives are used to analyze the impact of fractional parameters(memory effect)on the dynamics of the fluid.While making a comparison,it is observed that the fractional-order model is best to explain the memory effect as compared to classical models.Our results suggest that the velocity profile decrease by increasing the effective Prandtl number.The existence of an effective Prandtl number may reflect the control of the thickness of momentum and enlargement of thermal conductivity.The incremental value of the M is observed for a decrease in the velocity field,which reflects to control resistive force.Further,it is noted that the Atangana-Baleanu derivative in Caputo sense(ABC)is the best to highlight the dynamics of the fluid.The influence of pertinent parameters is analyzed graphically for velocity and energy profile.Expressions for skin friction and Nusselt number are also derived for fractional differential operators.

KEYWORDS MHD Maxwell fluid;fractional differential operator;heat generation absorption;thermal effect;non-singular kernels

1 Introduction

Viscoelasticity has important implications due to the characterization of viscoelastic parameters (relaxation and retardation phenomenon),elastic shearing strain,thermal relaxation,timedependent an elastic aspect,and other rheological properties [1-3].In such fluid,stress and rate of strain have a nonlinear relationship and enhance their order which makes the flow equation more complicated [4,5].Elastic and memory effect for the flow of rate type fluid discussed by Maxwell.

Firstly,Maxwell [6] analyzed the visco-elastic attributes of air.Fetecau et al.[7] investigate the closed-form solution of the Maxwell model over an unbounded plate.Moreover,authors [8]discussed the Maxwell model over unbounded plate swing in the plane.Some significant results of the Maxwell model can be studied in [9-12].Aman et al.[13] investigated the heat transfer analysis of Maxwell fluid flow with carbon nanotubes.The analytical solution of a Maxwell fluid with slip effects was investigated by Asif et al.[14].Further,authors [15] discussed the unsteady rotational flow of Maxwell fluid in a Cylinder subject to shear stress.Noor [16] analyzed the impacts of chemical reaction on MHD Maxwell fluid flow for a vertical stretching sheet.In the literature,all the above-mentioned articles dealing with the flow of uniform and constant boundary conditions.There is an insufficient study that deals with flows under ramped wall temperature and ramped wall velocity conditions.Physically,the implementation of ramped wall velocity and temperature in real-life problems has a significant role.The diagnoses of prognosis,establishing treatments,analysis of heart functions,and blood vessel system [17-20] are major applications of ramp velocity.Firstly,the authors [21] discussed the simultaneous use of ramped velocity and temperature.Seth et al.[22-24] investigated heat and mass transfer phenomena with ramp temperature conditions.Recently,Tiwana et al.[25] and Anwar et al.[26] analyzed MHD Oldroyd-B fluid in the presence of thermal radiation under the effect of ramped temperature and ramped velocity.Anwar et al.[27] analyzed the flow of MHD Maxwell fluid under the impact of ramped wall temperature and velocity.Shah et al.[28] analyzed the convection flow of viscous fluids with analytical results by employing the time-fractional Caputo-Fabrizio derivative.

The technique of fractional calculus has been used to formulate mathematical modeling in various technological development,engineering applications,and industrial sciences.Different valuable work has been discussed for modeling fluid dynamics,signal processing,viscoelasticity,electrochemistry,and biological structure through fractional time derivatives.This fractional differential operator found useful conclusions for experts to treat cancer cells with a suitable amount of heat source and have compared the results to see the memory effect of temperature function.As compared to classical models,the memory effect is much stronger in fractional derivatives.From the past to the present,modeling of the different processes is handled through various types of fractional derivatives and fractal-fractional differential operators,such that Caputo (Power law),Atangana-Baleanu (Mittage-Leffler law),Caputo-Fabrizio (exponential law),Riemann-Liouville,modified Riemann-Liouville (Power law with boundaries) and few others [29-36].Recently,Imran et al.[37] studied the comparison approach between Caputo-Fabrizio and Atangana-Baleanu fractional derivative and found that Atangana-Baleanu fractional derivative is excellent in exhibiting the memory effect in fluid flow problems.Convective flow with ramped wall temperature for non-singular kernel analyzed by Riaz et al.[38].Further,Riaz et al.[39] discuss MHD Maxwell fluid with heat effect using local and non-local operators.Moreover,the authors [40] analyze the comparative study of heat transfer of MHD Maxwell fluid in view of fractional operators.Khan et al.[41,42] discussed the heat transfer analysis in a Maxwell fluid using fractional Caputo-Fabrizio derivatives.Some recent studies related to the applications of modern techniques of fractional derivatives can be seen [43-48].

The main objective of this paper is to investigate the MHD Maxwell model with the definition of fractional order derivative in a Darcy medium.The solution of fluid velocity,energy,and shear stress are obtained by Caputo-Fabrizio (CF)and Atangana-Baleanu derivative in Caputo sense(ABC)fractional derivative models under influence of ramped velocity and temperature.These non-integer order derivatives are good for handling the mathematical calculation.Section 2 helps to derive the governing partial differential equations.The solution of the temperature profile,velocity profile,and shear stress can be achieved throughCFandABCfractional models with help of Laplace transformation and inversion algorithm in Sections 3 and 4 respectively.In Section 5,the influence of physical parameters is discussed graphically by MATHCAD-15 software.Finally,the conclusion of the present article is given at the end.

2 Development of Governing Equations Based on Problem Statement

Consider the MHD time-dependent Maxwell model over an unbounded vertical plate immersed in a permeable surface.The plate is along the x-axis,while theξ-axis is perpendicular to the plate.At the wall end,both velocity and temperature have time-dependent conditions up to some certain limit of time known as the characteristic time;after that time,both velocity and temperature attain constant valuesu0andT∞.The physical model expressed in Fig.1.Under these presumptions,the governing equation for MHD Maxwell fluid with appropriate conditions are given below [27,41]:

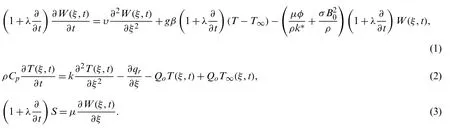
Figure 1:Geometrical presentation for MHD Maxwell model

Eqs.(1)-(3) represent as governing equations of velocity,energy and shear stress distributions respectively subject to imposed conditions as:

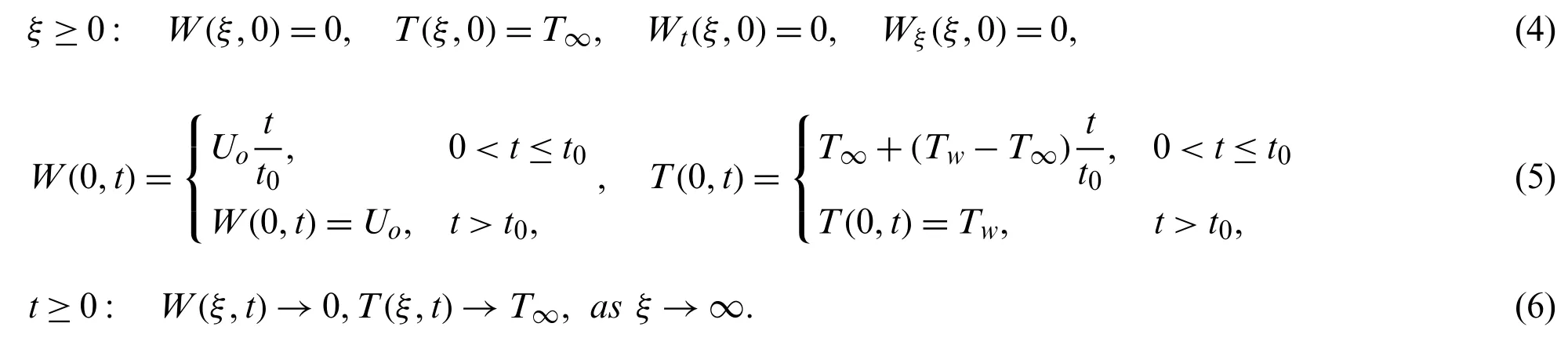
Introduce dimensionless elements to form the problem free from geometric

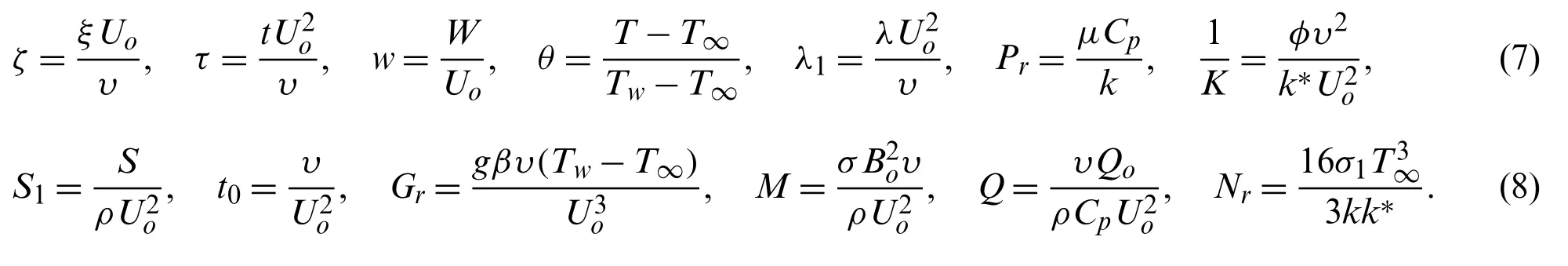
After simplification,we have the set of dimensionless governing equations:

with corresponding conditions

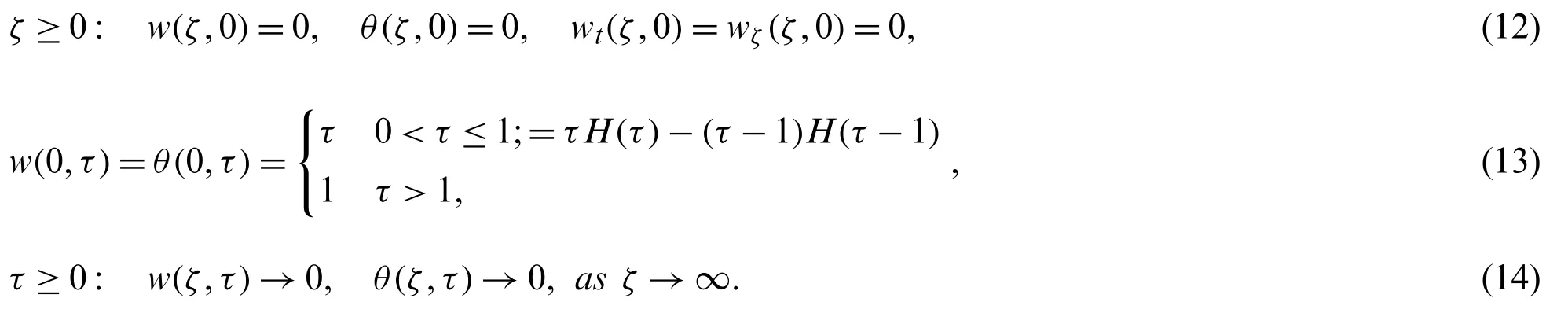
3 Solution of Temperature Profile

3.1 Caputo-Fabrizio Fractional Derivative

Fractional operators are quite flexible for describing the behaviors of energy transfer of MHD Maxwell fluid through the characterization of governing equations.Generating fractional governing equation of temperature (10) via CF-fractional operator (16) by exchanging the partial time derivative with fractional derivative of orderκ,

where,CFDκtis known as CF fractional operator [32] is defined by

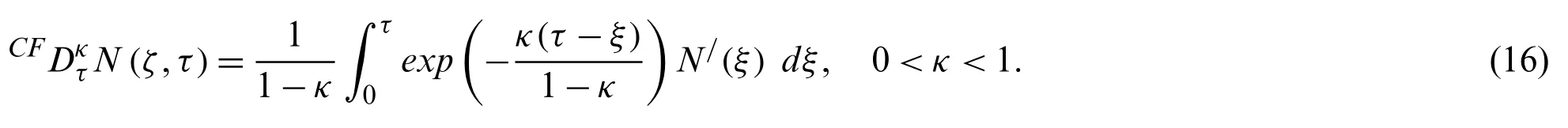
Solving the uncoupled and fractionalized governing equation of temperature (15) by Laplace transform method.One has to need the following typical property of Caputo-Fabrizio fractional operator defined in Eq.(17)

employing Laplace transformation on (15) with the help of (17),we explored second order partial differential equation

More suitable form of temperature field is

The solution of homogenous part of second order partial differential equation say (19) is,

with the help of Eqs.(12)-(14),we find out the values of constantsc1andc2for temperature equation

where

g1=1+Q−κQ,g2=κQ,g3=1−κ,g4=κ.

The expression of Nusselt numberNuforCFdifferentiation is given as:

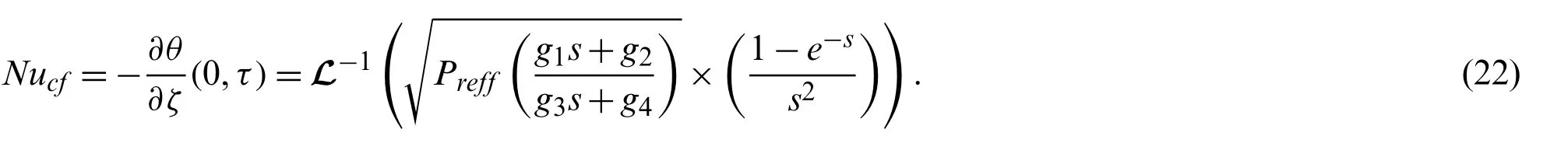
3.2 Atangana-Baleanu Fractional Derivative

Generating a fractional governing equation of temperature (15) via ABC-fractional operator (24) by exchanging the partial time derivative with fractional derivative of orderγ,

whereABCDγtis known as ABC fractional operator [33] is defnied by

whereM(α)denotes a normalization function obeyingM(0)=M(1)=1.

Solving governing equation of temperature (23) by Laplace transform method.One has to need the following typical property of ABC-fractional operator defined in Eq.(25)

employing Laplace transformation on (23) with the help of (25),we explored second order partial differential equation:

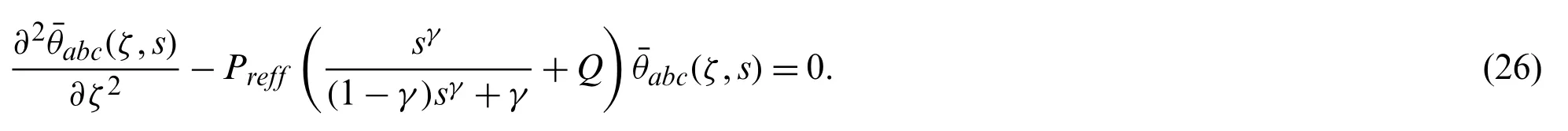
More suitable form of temperature field is,

The solution of homogenous part of second order partial differential equation say (27),

with the help of Eqs.(12)-(14),we find out the values of constantsc1andc2for temperature equation:

where

h1=1+Q−γ Q,h2=γ Q,h3=1−γ,h4=γ.

The expression of Nusselt numberNuforABCdifferentiation is given as:

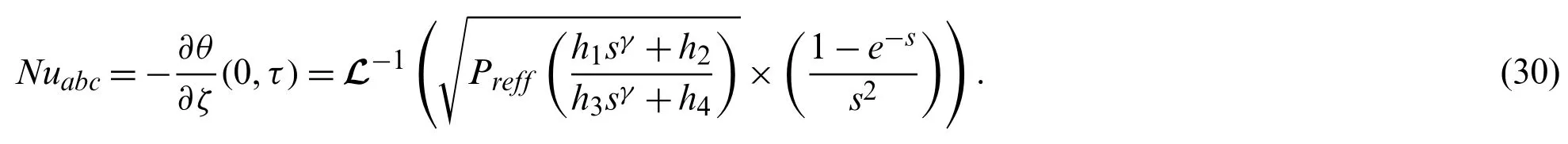
4 Solution of Velocity Profile

4.1 Caputo-Fabrizio Fractional Derivative

Generating a fractional governing equation of velocity Eq.(9) via CF-fractional operator say equation Eq.(16) by exchanging the partial time derivative with fractional derivative of orderκthen solving the governing equation Eq.(9) by Laplace transform method,we get

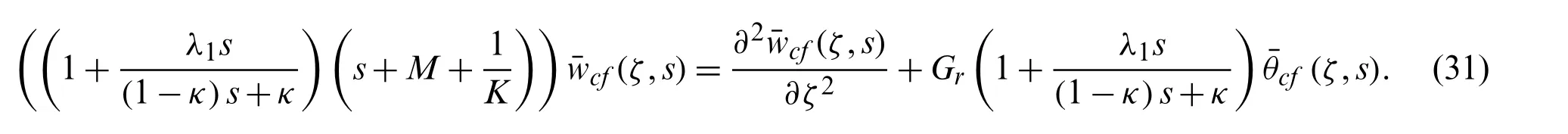
The required homogeneous part of the Eq.(31) is given as:

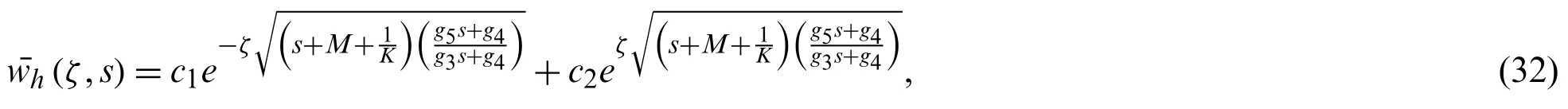
and particular solution can be give as follow after making use of Eq.(18),

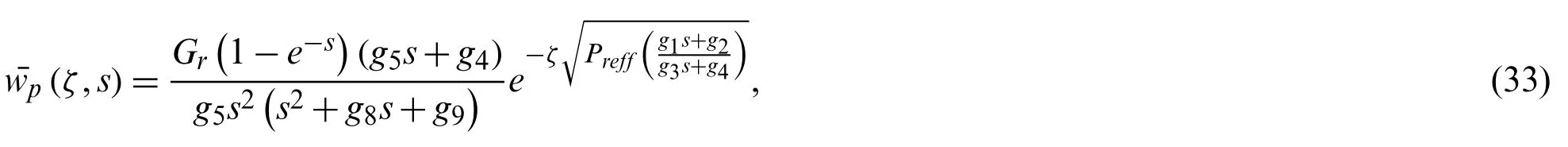
and solution of Eq.(31) can be given as follow:

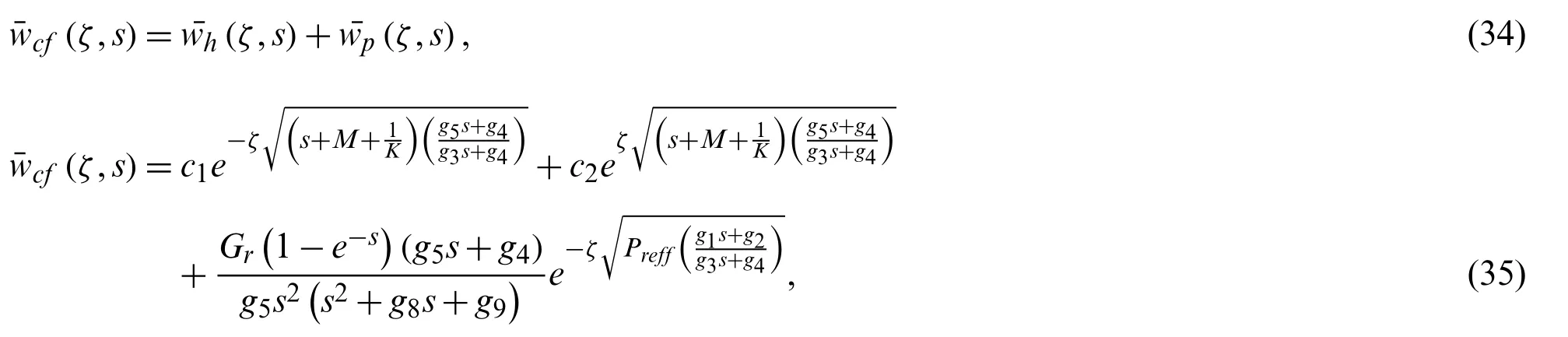
using conditions given in Eqs.(12)-(14) for velocity in order to find constants,we have

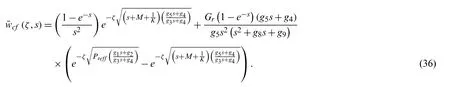
The suitable and simplified form for inversion algorithm,we have

and

where,letting parameters are described as

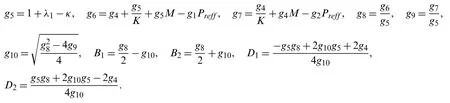
Differentiate Eq.(37) with respect toζ,we have

where

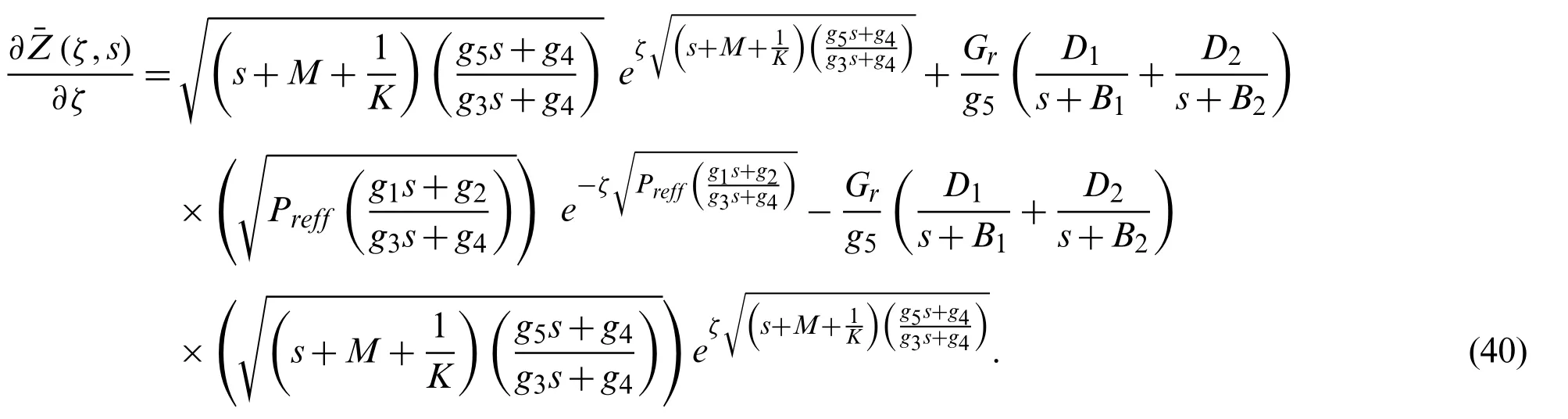
Plugging Eq.(38) into Eq.(11) gives the resultant solution of shear stress

The expression of skin frictionSfforCFdifferentiation is given as:

4.2 Atangana-Baleanu Fractional Derivative

Generating a fractional governing equation of velocity Eq.(9) via ABC-fractional operator say equation Eq.(24) by exchanging the partial time derivative with fractional derivative of orderγthen solving the governing equation Eq.(9) by Laplace transform method,we get

The homogeneous part of the Eq.(43) is given as:

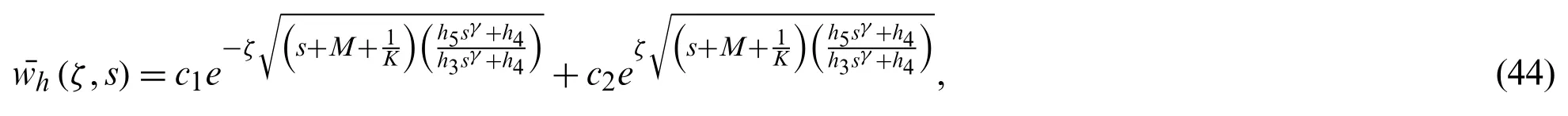
and particular solution can be give as follow after making use of Eq.(29) for the values(ζ,s),

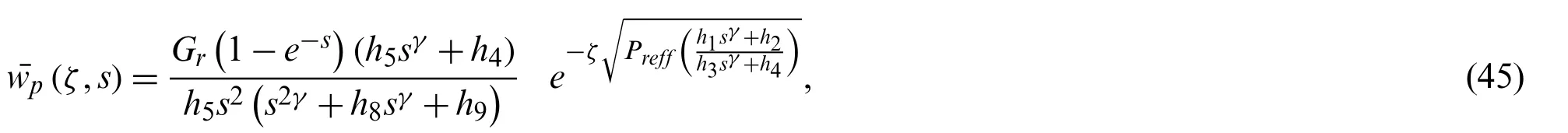
using conditions given in Eqs.(9)-(11) for velocity in order to find constants,we have

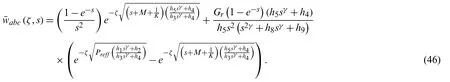
The suitable and simplified form for inversion algorithm,we have

and

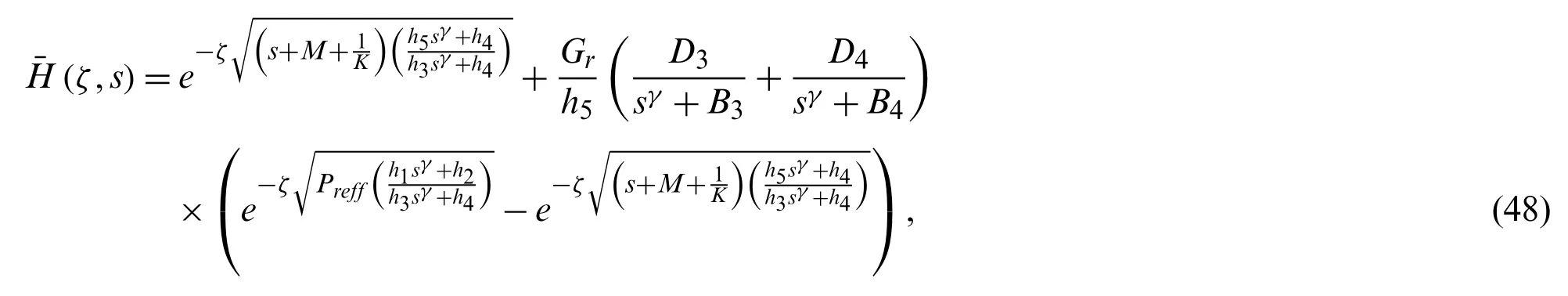
where,letting parameters are described as

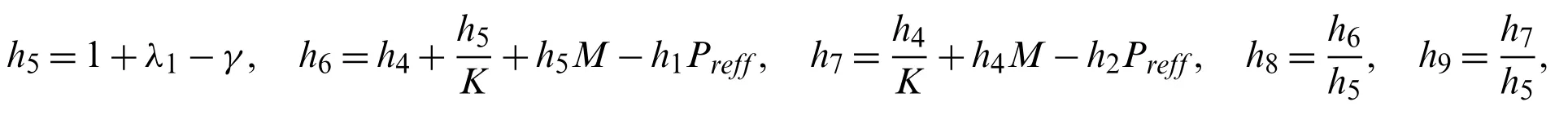
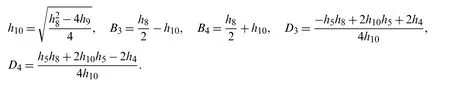
Differentiate Eq.(47) with respect toζ,we have

where

Plugging Eq.(50) into Eq.(11) gives the resultant solution of shear stress:

The expression of skin frictionSfforABCdifferentiation is given as:

In our flow models we use classical computational technique (Laplace transform) to solve the given models using different definitions of fractional derivatives.There are many algorithms for the numerical calculation of the inverse Laplace transform.The Stehfest’s formula,which approximates the inverse Laplace transform is simple,easy to use compared with other algorithms.In this paper we use Stehfest’s algorithm and also give comparison with other in tabular form.Tzou’s calculation for approval of our numerical inverse Laplace

where Re(.) is the real part,i is the imaginary unit andN1is a natural number [49,50].

5 Results and Discussion

This section is dedicated to present physical interpretation of the obtained results via CF and AB differential operators under heat generation,ramp velocity,and ramp temperature on the MHD Maxwell model.Results are investigated via Laplace transformation with an inversion algorithm for velocity,energy,and shear stress based on singular verses non-singular and local versus non-local kernels.The graphical representations are depicted for showing the influences of different physical parameters such as effective Prandtl numberPreff,thermal Grashof numberGr,fractional parametersγand magnetic effectMon velocity and energy profile using the package of MATHCAD-15.Additionally,we focus our depicted graphs for the comparison of ramped temperature with constant temperature using a fractional operator.

Figure 2:Plot via CF and AB-approaches for temperature with variation of Preff and time

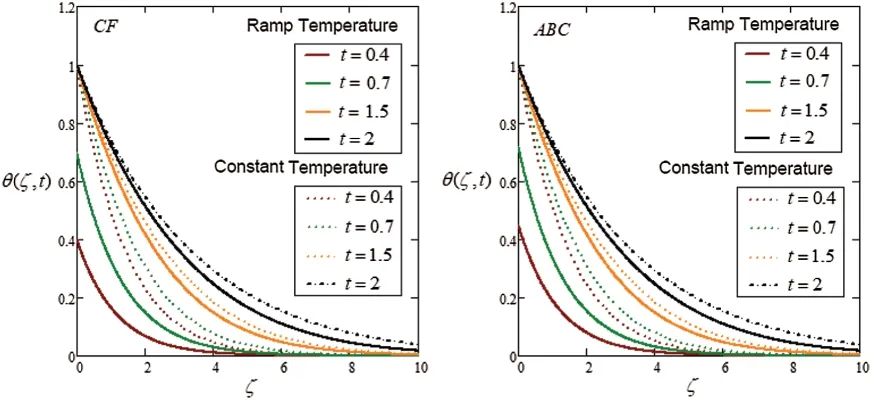
Figure 3:Plot via CF and AB-approaches for temperature with different values of time effect

Fig.2 is plotted for the impact ofPreffon the energy profile.It is seen that the thermal layer and temperature decrease by a large value ofPreff.AsPreffincreases,the temperature profile reduces more rapidly on theABCmodel as compared to theCFmodel.Physically,for a small value ofPreffthermal conductivity enhances which allows heat to diffuse away rapidly for a higher value ofPreff.For the isothermal case,the energy solution has a higher profile.The influence of time on the temperature field can be analyzed in Fig.3.ForCFandABCmodels,as an increase in time effect the resultant energy profile reduces for both ramped and isothermal wall conditions.

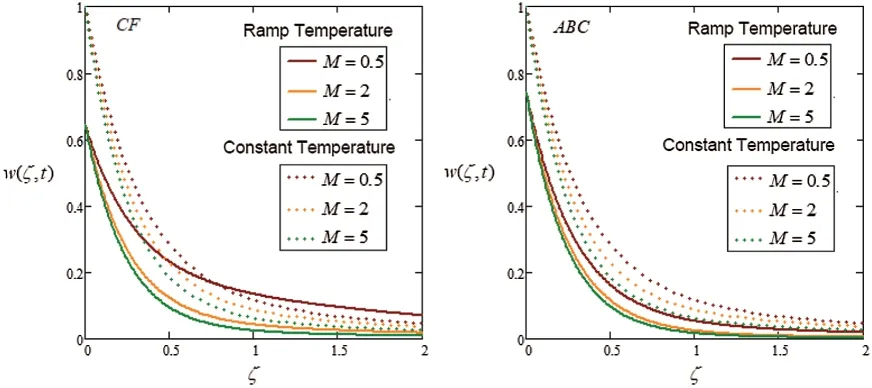
Figure 4:Plot via CF and AB-approaches for velocity with variation of time and M

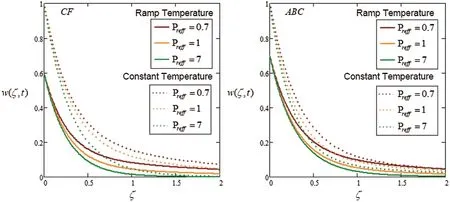
Figure 5:Plot via CF and AB-approaches for velocity with variation of time and Preff

Fig.4 investigates the influence ofMon velocity components.This graphical representation indicates that an increase in the magnetic field,the velocity reduce due to Lorentz force.It behaves as a drag force.By increasing the parameter of the magnetic field,the Lorentz force also increases.Fluid flow on the boundary layer is slow down due to this force.Fig.5 investigates the behavior ofPreff.Specific heat and conductivity depend onPreff.The thickness of the momentum and boundary layer is control by an effective Prandtl number.It is seen from the graph,decreasing the velocity,observed by increase the value ofPreff.The lower effective Prandtl number enhances thermal conductivity and increase the boundary layer.

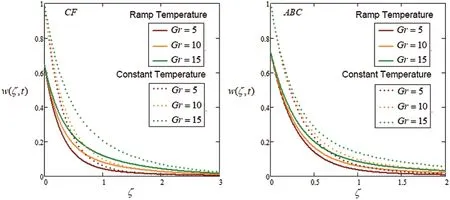
Figure 6:Plot via CF and AB-approaches for velocity with variation of time and Gr

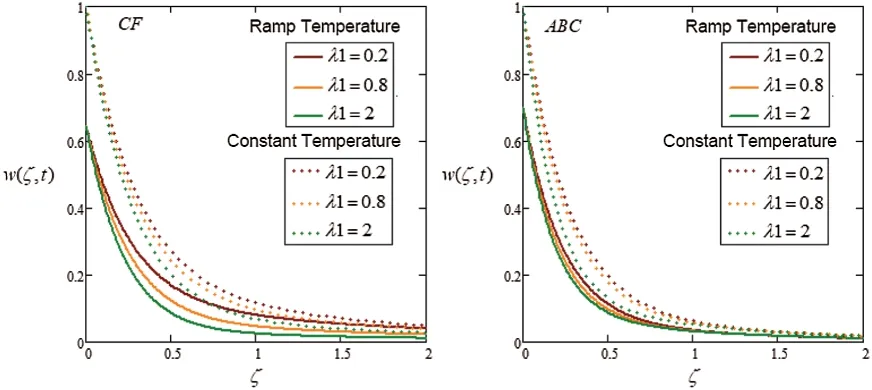
Figure 7:Plot via CF and AB-approaches for velocity with variation of time and λ1

Fig.6 shows that the impact onGrfor the velocity field versus time.It is the ratio of the buoyancy to a viscous force acting on the fluid.It can be seen in the velocity field enhance by increasing inGr.In a physical sense,as expected,when the Grashof number is increased,then fluid flow rises due to the thermal buoyancy effects.The velocity for theABCmodel is good as compare toCFmodels.It is observed that velocity for the isothermal condition is always larger than ramped conditions.Fig.7 analyzes the unique role ofλ1for ramped wall and isothermal wall conditions.The value ofλ1enhances leads to reduce in velocity.In the physical sense,relaxation describes the return of a perturbed system to a state of equilibrium.

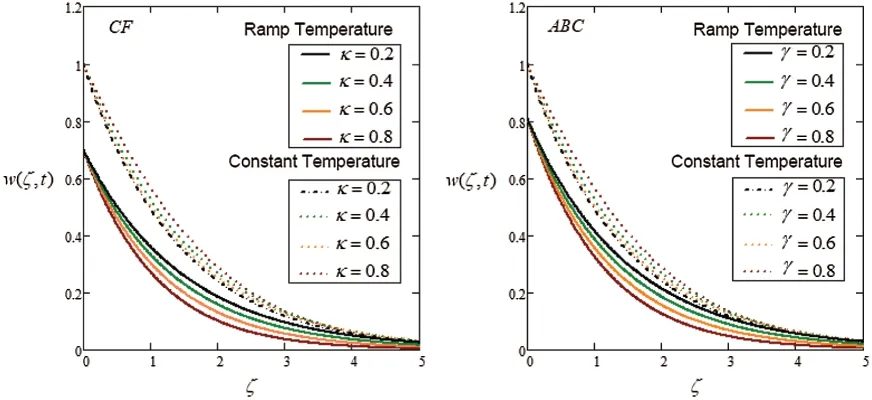
Figure 8:Plot via CF and AB-approaches for velocity with variation of time and γ

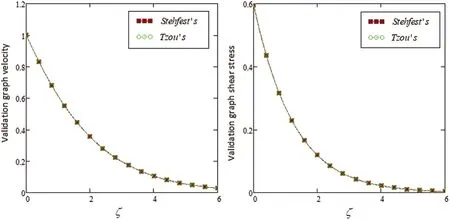
Figure 9:Comparison via Stehfest’s and Tzou’s algorithm

The influence ofαon the velocity field can be analyzed in Fig.8.The velocity field reduces by increasing the value ofαfor bothABCandCFmodels.The flow behavior for isothermal and ramped conditions are the same in all cases.To validate our solutions obtained by means of numerical inversion Laplace transform namely,Stehfest’s and Tzou’s algorithm.We represent the equivalence relation between those techniques in Fig.9.

Fig.10 is plotted to see the validity of our obtained results.We have compared our temperature results with the results from the studies by [26,27].In Fig.11,our obtained results are compared with the results of [22,26].

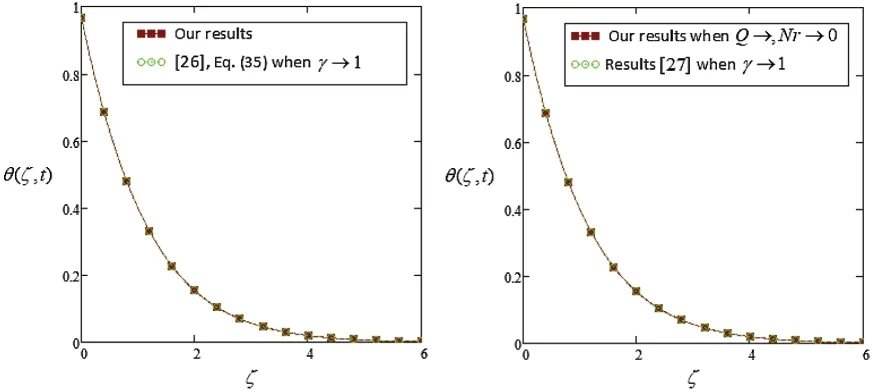
Figure 10:Temperature profile of our models compared with [26,27]

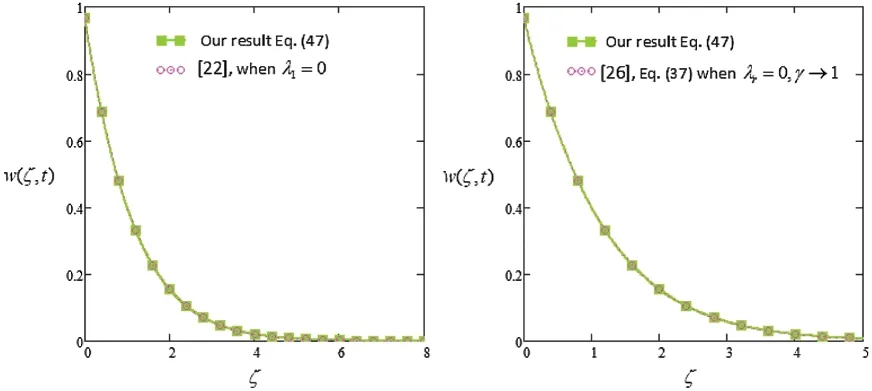
Figure 11:Velocity profile of our models compared with [26,27]

Tabs.1 and 2 represent a comparison of the temperature profile betweenCFandABCusing Stehfest’s and Tzou’s algorithms with a variation ofPreff.It is observed that the temperature profile reduces with large values ofPreff.It is noted that the temperature is maximum in theABCmodel as compared toCF.Tabs.3 and 4 represent a comparison of the fluid velocity between CF and ABC for increasing values ofζby using inversion algorithms.Velocity increases for all models.The velocity obtained via the ABC approach is greater than the velocity computed with the help of the CF approach.Some numerical calculations for the Nusselt number forPreffhave been carried out by Stehfest’s and Tzou’s algorithms in Tabs.5 and 6.It can be seen that the rate of heat transfer rate is high for the ABC model as compare to other models.

Table 1:Numerical inversion Laplace transform for temperature by Stehfest’s and Tzou’s

Table 2:Numerical inversion Laplace transform for temperature by Stehfest’s and Tzou’s

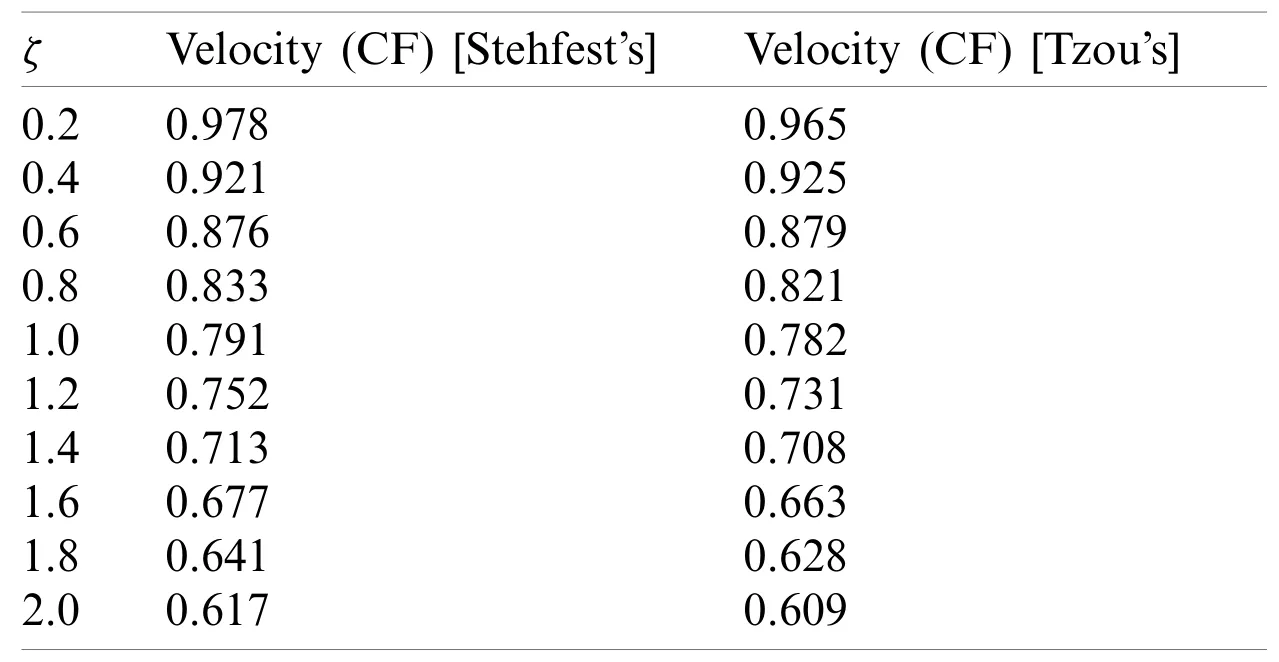
Table 3:Numerical inversion Laplace transform for velocity by Stehfest’s and Tzou’s

Table 4:Numerical inversion Laplace transform for velocity by Stehfest’s and Tzou’s

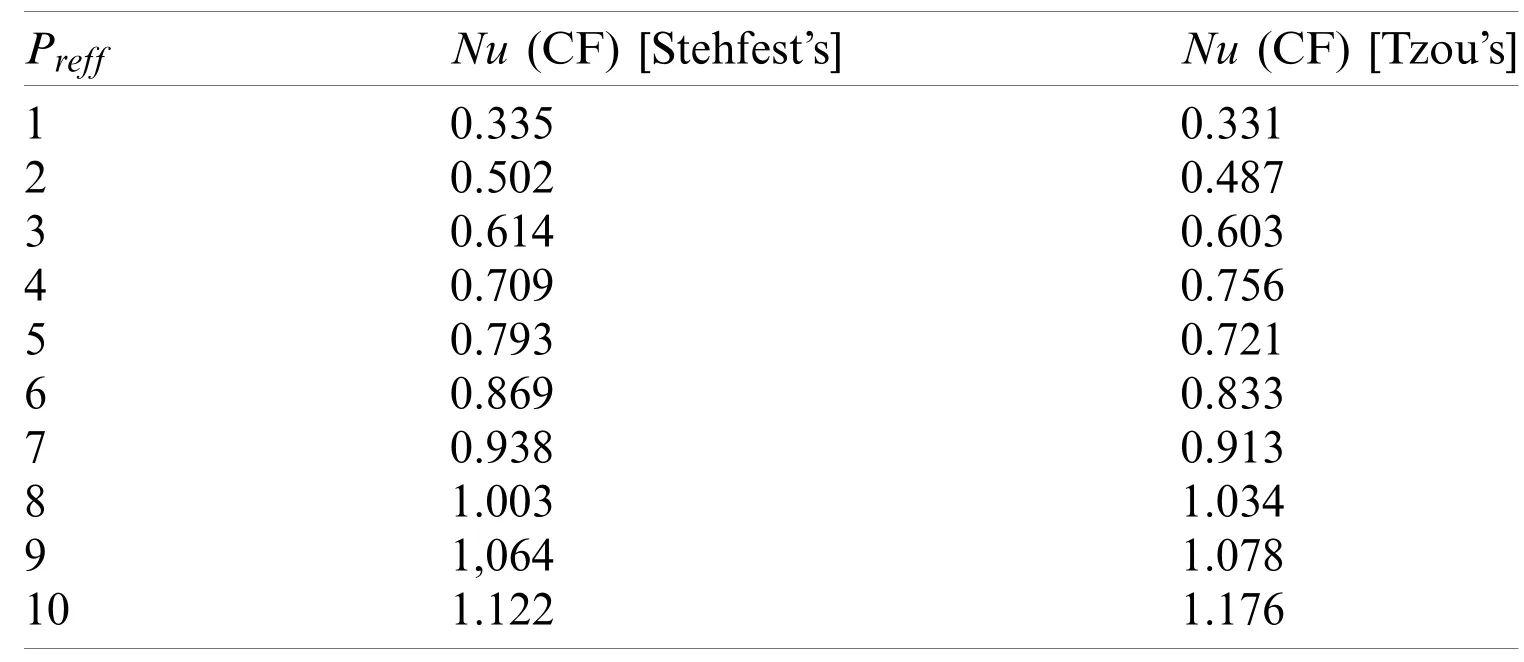
Table 5:Numerical inversion Laplace transform for Nusselt number by Stehfest’s and Tzou’s

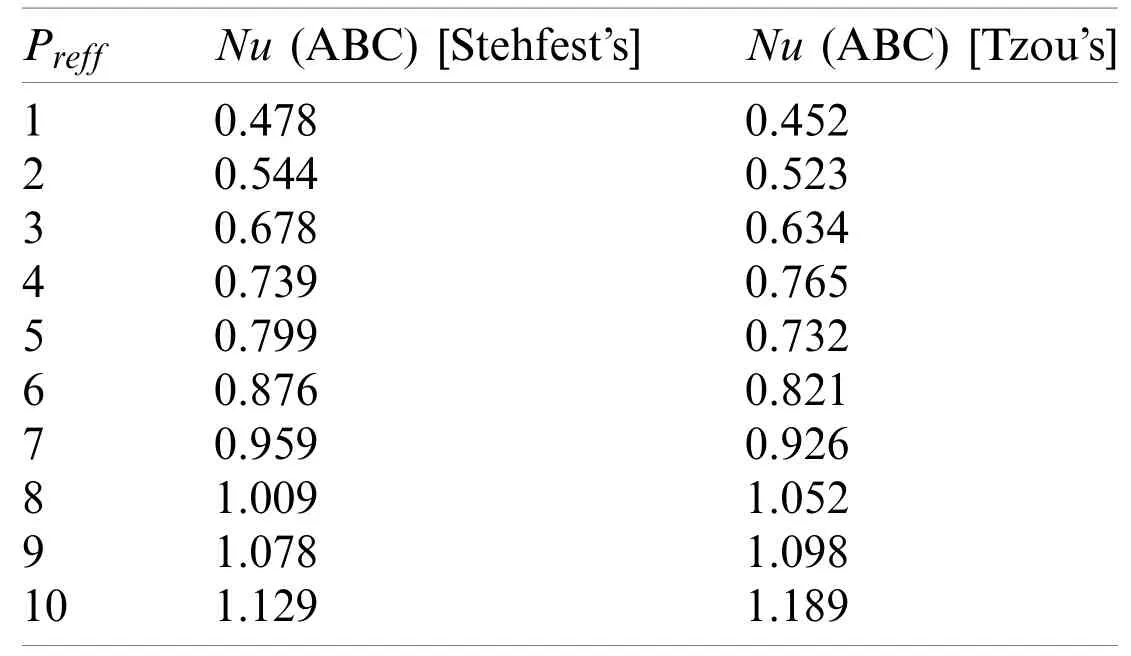
Table 6:Numerical inversion Laplace transform for Nusselt number by Stehfest’s and Tzou’s

6 Conclusion

The basic purpose of this article was to investigate the effect of the simultaneous use of ramped velocity and ramped temperature conditions on MHD Maxwell fluid.It is difficult to calculate the solutions of MHD Maxwell fluid using both ramp conditions.Fractional differential operators are used to finding solutions using Laplace transformation and inversion algorithm.Some comparisons have been drawn and they are in good agreement with the results published in [22,26,27].The important finding of this investigation are:

• The velocity decreases by magnifying the value of the magnetic profile.

• The velocity increases with increasing values ofGr.

• The Nusselt number describes that the heat transfer rate enhances with increasing thermal diffusivity.

• The velocity decreases by magnifying the value of thePreff.

•ABCfractional derivative is more considerable as compared to the classical model and other fractional models.

Acknowledgement:The authors are highly thankful and grateful for generous support and facilities of this research work.

Funding Statement:Self supported by the authors.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.