基于循环谱的外辐射源无人机微动特征检测*
谢跃雷,刘 信,梁文斌
(1.桂林电子科技大学 a.信息与通信学院;b.广西无线宽带通信与信号处理重点实验室;c.信息科技学院,广西 桂林 541004)
0 引 言
随着科技发展,小型无人机的功能越来越强,成本越来越低,在军事领域和民用领域都得到广泛应用。但在无人机市场持续增长的同时,无人机黑飞现象愈发频繁,“扰航”“伤人”“偷拍”等事件不时发生,甚至被用于走私和恐怖袭击等犯罪活动[1-3]。为遏制无人机黑飞的蔓延,目前全球各国都开始加强无人机监管,如何有效探测和识别无人机成为无人机监管的关键。
小型无人机几乎都有一个及以上数目的旋翼,旋翼的转动会对散射的电磁波信号进行周期性的调制,产生微多普勒效应[4-5]。微多普勒效应包含了无人机目标独特的微动特征,这为无人机的探测和识别提供了新的解决方法[6-12]。文献[6-7]分别通过实验测试了无人机的微多普勒效应,在入射电磁波与旋翼轴呈多种夹角及非视线条件下,单翼转动或多翼同时转动,接收回波信号中均存在明显的微多普勒效应,表明微多普勒特征可以作为探测小型无人机的一个明显特征。文献[9]中提出了一种基于经验模态分解的无人机微多普勒分类方法,通过本征函数估计出微多谱勒特征,实现了准确的无人机分类识别。虽然以上研究都可有效检测出无人机的微动特征,但实际应用中均需发射一定功率的雷达信号,易造成电磁污染,部署成本相对较高。
外辐射源雷达利用广播、电视及移动通信信号等非合作辐射源进行目标检测,无需发射信号且成本低,为无人机的检测提供了新的途径。文献[10-11]研究了第三方非合作照射源条件下目标的微多谱勒效应,实验中采用广播电视信号作为外辐射源,发现旋转的螺旋桨仍然可以引起明显的微多普勒效应。文献[12]进一步研究了数字电视外辐射源下多旋翼无人机微多普勒效应,给出了外辐射源雷达无人机微动信号模型,阐述了微动信号提取的关键技术,实验测试结果证实了利用数字电视外辐射源雷达实现多旋翼无人机微多普勒效应探测的技术可行性。以上微动特征检测方法需要重构参考信号,并采用直达波及多径杂波抑制算法来增强微多普勒特征信号,复杂度较高。
针对外辐射源雷达无人机微动特征检测问题,本文以数字电视地面广播(Digital Terrestrial Multimedia Broadcast,DTMB)信号作为非合作辐射源,提出一种基于二阶循环谱的微多普勒特征提取算法。数字电视地面广播信号采用DTMB标准,属于正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)类的多载波信号,具有循环平稳特性。而由文献[13-15]的研究可知,微动引起的微多普勒特征信号是非平稳信号,但也具有循环平稳特性。本文选取消费级无人机市场上的主流无人机大疆精灵4pro作为研究目标,建立相关参数模型,利用学校附近的尧山广播电视塔发射信号作为无源雷达的辐射源。
1 无源雷达回波信号模型及成分分析
本文采用DTMB地面数字电视广播信号作为无源雷达发射信号,DTMB系统采用了TDS-OFDM调制方式,其特点是帧头采用PN序列,帧体采用多载波调制,PN序列和多载波模式可以认为是时域的PN序列和频域的OFDM符号在不同的时间片上传输。假设PN序列的长度为Ng(420、595和945),并且OFDM符号的长度为N1。PN序列和OFDM帧体的组合构成了一个完整的信号帧。
第l帧中的第k个符号表示为
(1)
式中:
(2)
式中:l为帧数,k为同一帧中的符号数,PNk表示帧同步头中的符号。sl,k是来自有限星座的数据符号,Sl,i是在星座之后的频域中的数据符号,因此DTMB信号的复包络为
(3)
式中:cl,k是复信息符号,gtr(t)是发射器的信号脉冲,t0为脉冲起始时间,T0是符号周期,fc是载频。

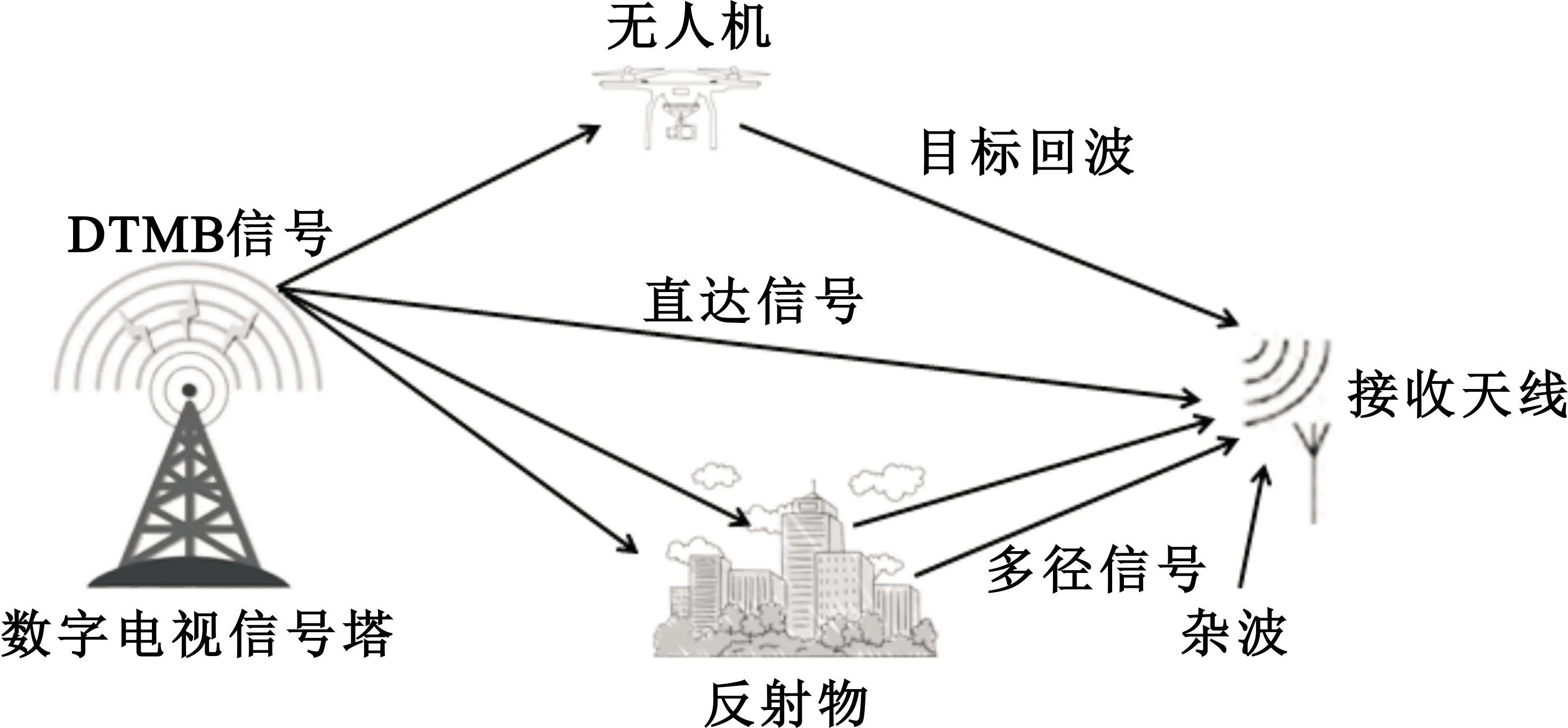
图1 DTMB信号传播形式
根据学者Chen[5]对雷达中微多普勒特征的数学推导,设无人机旋翼为一散射点目标,则目标相对雷达的径向运动规律R(t)为
R(t)=R0+Apcosβsin(2πfrt+φ0)。
(4)
式中:R0是旋转中心到雷达的距离,Ap为旋翼长度,φ0为旋翼初始相位,fr为转动频率。
无人机微动产生的目标回波x(t)可以表示为
x(t)=y(t-τ)=
(5)
式中:ρ为散射中心的后向散射强度,τ=2R(t)/c,c为光速。
所以总的接收信号z(t)为
z(t)=y1(t)+y2(t)+x(t)+n(t)。
(6)
直达信号y1(t)、多径信号y2(t)和目标回波x(t)经过过采样后具有循环平稳特性,而高斯白噪声n(t)不具备周期平稳性,即当循环频率不等于0时,高斯白噪声的循环谱密度函数在理论上为0。因此对于接收信号而言,在循环谱的非零循环频率域上能够抗高斯白噪声干扰,具有较强的抗噪声性能。在目标回波x(t)中,微多普勒特征会在DTMB信号上产生微弱的调制,从而与直达信号y1(t)和多径信号y2(t)区分开。直达信号y1(t)和多径信号y2(t)相当于DTMB经过莱斯信道后产生的,由文献[16]可知它们都满足相同周期的二阶循环平稳特性,即在循环谱上产生相同峰值,所以在检测时归为一类考虑。
2 循环谱检测及仿真验证
2.1 DTMB信号循环平稳特性
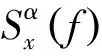
(7)
式中:α是循环频率,f是谱频率,m是整数;G*(f)是G(f)的共轭,G(f)为成形滤波器,它的表达式为
(8)
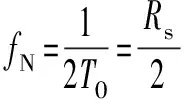

(9)
2.2 微多普勒特征循环平稳特性
由文献[14]可知,散射点转动的微多普勒特征的一般形式为正弦调制相位信号,模型如下:
r(t)=σrexp(jAsin(2πfvt-φ)),0≤t≤T。
(10)
为了方便推导微多普勒特征的循环平稳特性,假定式(10)中σ=1,φ=0;fv为微多普勒频率,与转动周期有关。则微多普勒特征的观测模型为
r(t)=exp(jAsin(2πfvt))。
(11)
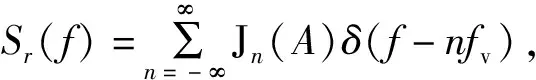
(12)
对于x(t)的二次变换
yτ(t)=r(t+τ/2)r*(t-τ/2)=
其中Fourier系数为
(13)
循环谱定义为循环自相关函数的傅里叶变换,即
(14)
将式(13)代入式(14),可得信号的循环谱为
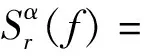
sinc[π(fv(m-n)-α)T]。
(15)
当且仅当
(16)
时循环谱不为零。考虑循环谱的峰值大小,设cmn=|sinc[π(fv(m-n)-α)T]|,则满足式(16)的情况下,循环谱为一系列的峰值:
(17)
所以,在循环谱f=0截面上,即m=-n时,在α=2nfv(n=±1,±2,±3…)处出现峰值。
2.3 理论仿真
本节仿真实验采用DTMB作为无源雷达,信号参数如表1所示;大疆精灵4pro作为检测目标无人机,参数如表2所示。
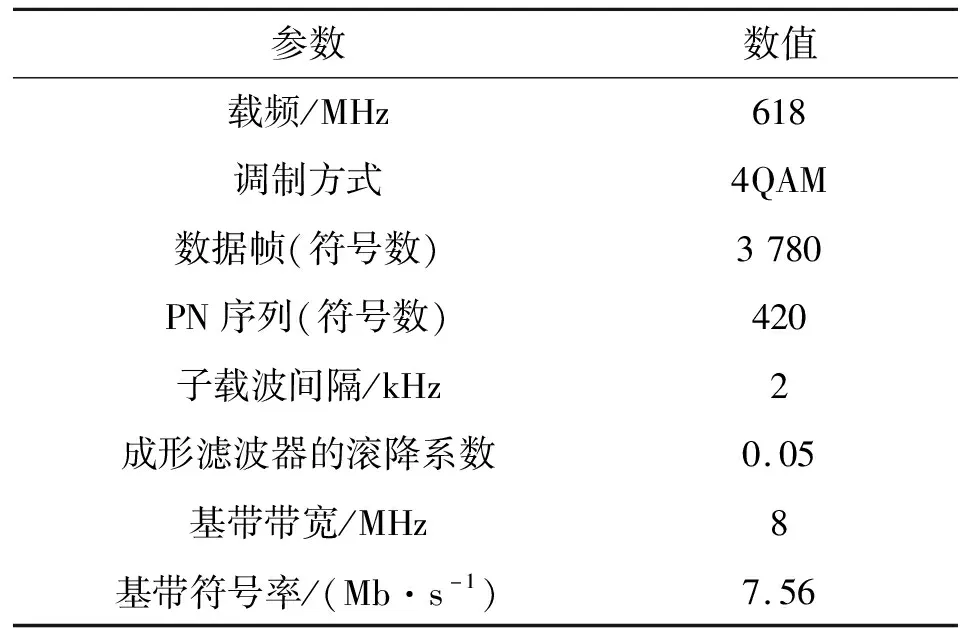
表1 DTMB信号参数

表2 大疆精灵4pro参数
图2证明了信号的谱相关密度函数是一个形式上的二维傅里叶变换频谱,其反映了频谱搬移过程在循环频率α=±2fc分量处的相关性。从图3(a)可知,频谱峰值之间的间隔为60 Hz,所以此时微多普勒频率fv=60 Hz;相应地,图3(c)中的次高峰出现在±2fv=±120 Hz处。上述仿真结果与理论相符。
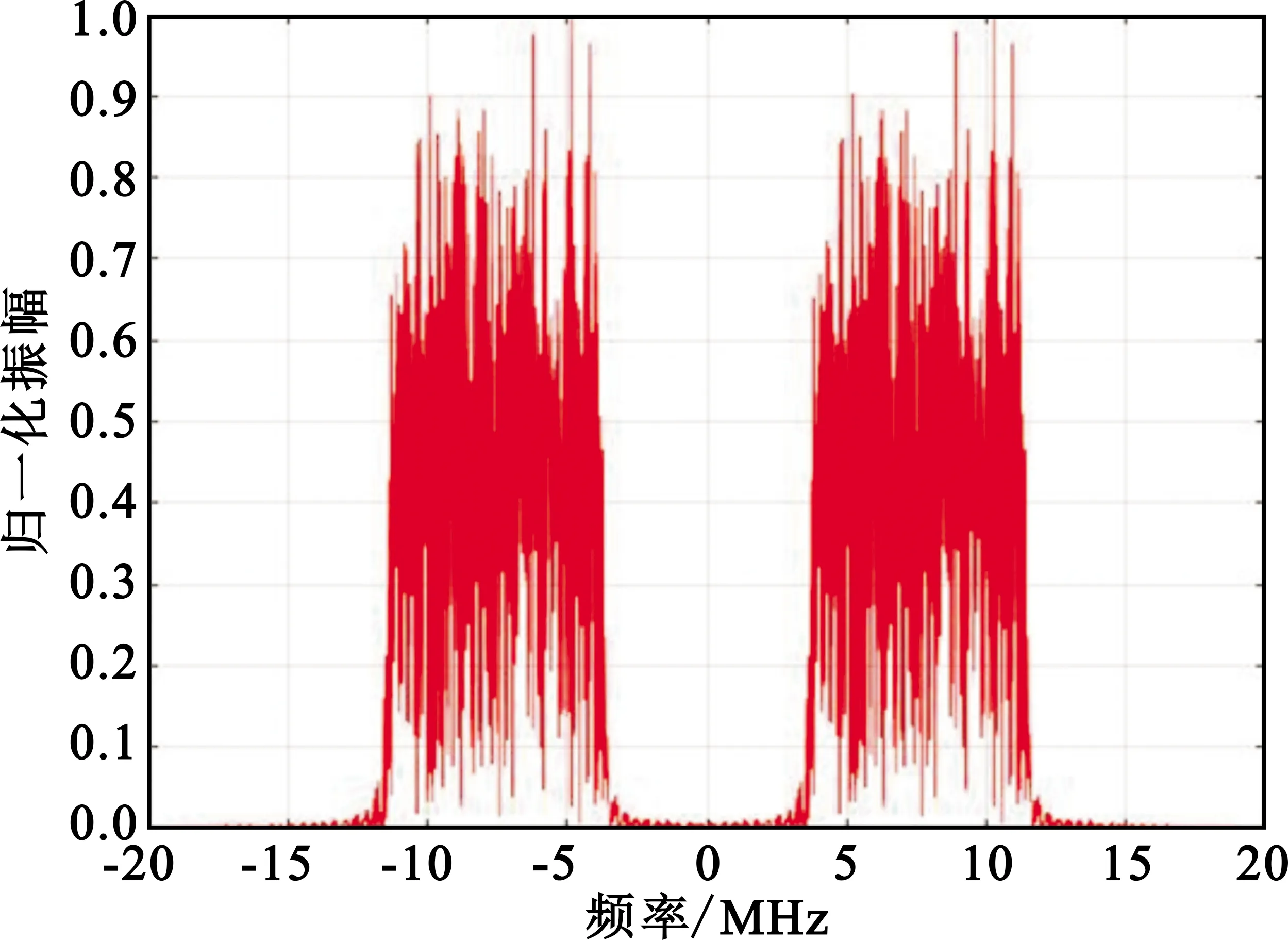
(a)DTMB基带信号的频谱
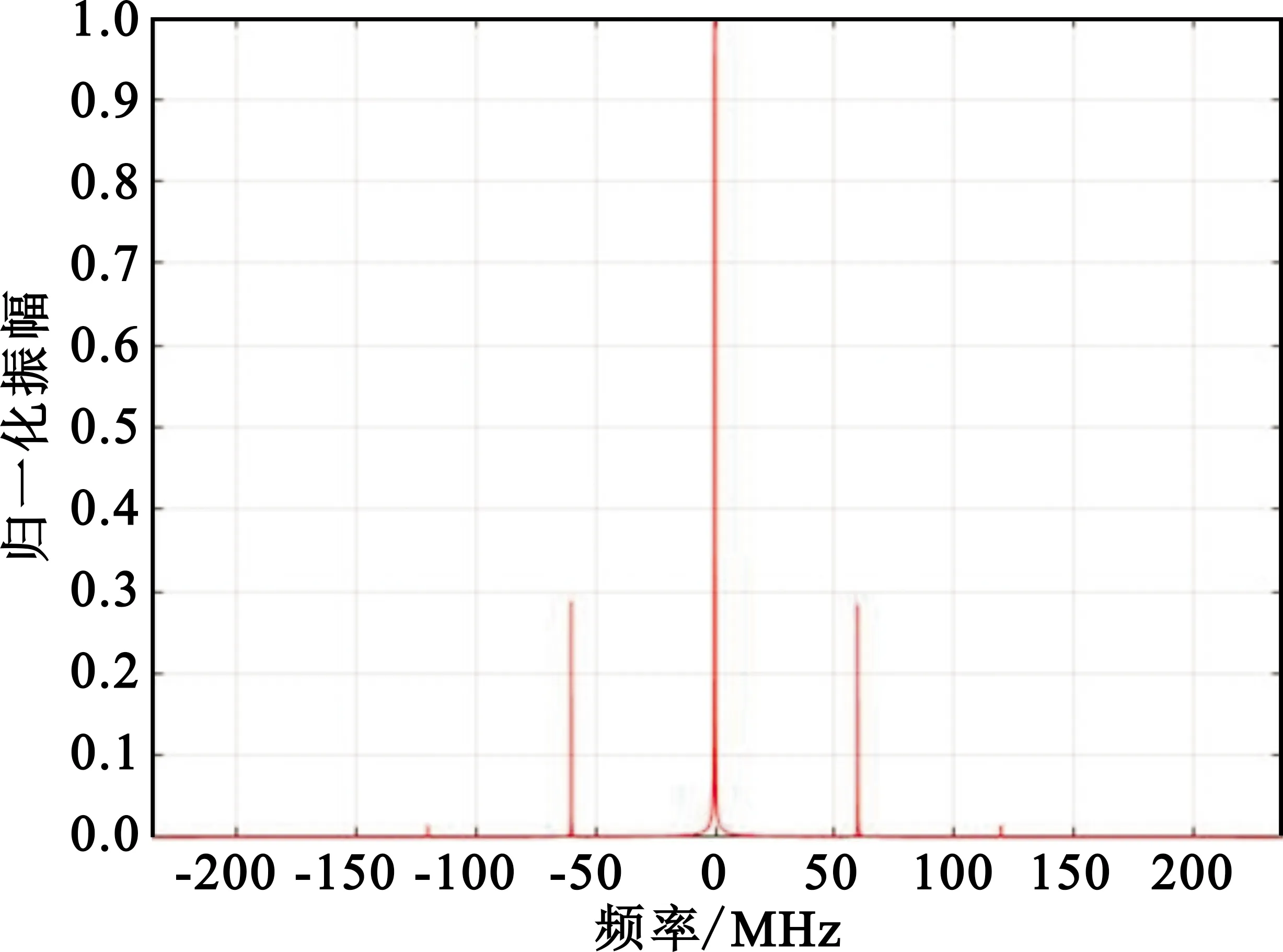
(a)微多普勒特征信号的频谱
文献[20]也是利用循环谱检测无人机的微动特征,但观察信号的三维循环谱难以直观地将不同调制方式信号之间的差异体现出来。本文检测方法作为该文献的扩展,对信号的循环谱等高图进行研究。循环谱等高图可以理解为等能量点的连接形成的,不同调制信号的等高图是不同。这表明,微动调制会对信号的循环谱等高图产生影响,从而利用该特征达到检测无人机的目的。并且,本文还增加无人机在不同飞行速度和转速下的仿真实验。
2.3.1 不同飞行速度和转速对等高图的影响
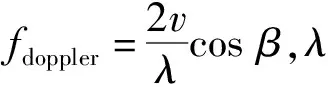
图4 无人机不同飞行速度的等高图和对微多普勒频谱的影响
无人机转速增大,会使微多普勒频率增大。本实验设置无人机转速分别为20 r/s、25 r/s、30 r/s、35 r/s、40 r/s,对应微多普勒频率分别为40 Hz、51 Hz、60 Hz、70 Hz、80 Hz。然后通过Matlab仿真得到对应的等高图,接着灰度化后,计算出不同转速下的总灰度值分别为57 587 532、5 758 8047、57 587 879、57 588 643、57 588 615。不同转速下的等高图与DTMB信号的等高图仍然有明显的区别,且不同的转速对等高图的影响不大。上述两个仿真实验证明了本文方法能有效检测到运动状态下的无人机。
2.3.2 无人机微动特征检测流程
信号的循环谱等高图是信号的循环平稳性和能量分布情况的表征,能量分布会通过不同颜色表示,通常为RGB三原色。等高图通过加权平法公式Gray=0.299R+0.587G+0.114B得到相应的灰度值,每个像素点的灰度值大小在0~255之间,0代表黑色,255代表白色。经过微动调制的回波信号与DTMB的循环谱等高图之间在能量分布上存在一定的差异。所以,利用以上信息,设计如图5所示的检测流程。
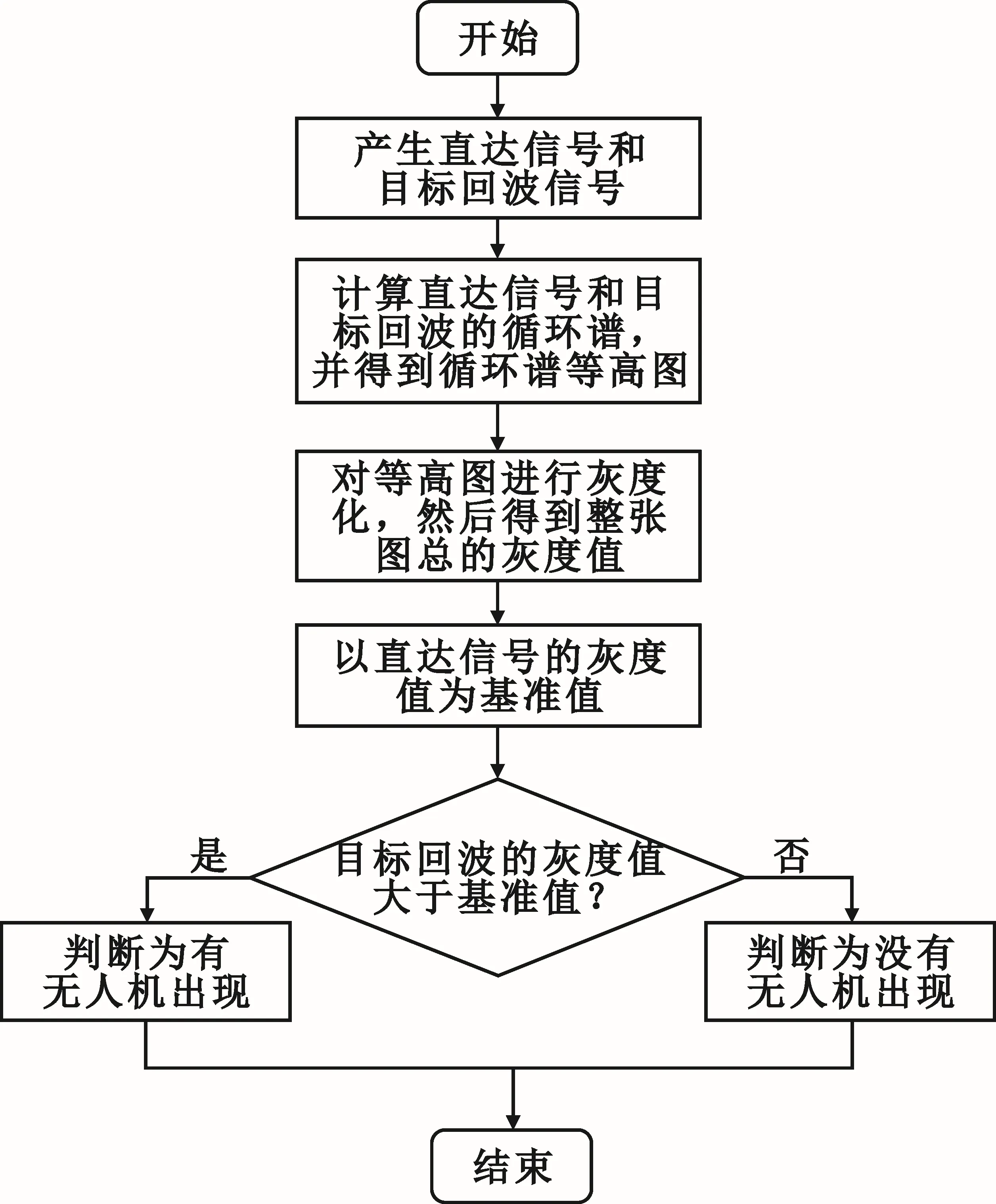
图5 检测流程图
根据上述检测流程,进行蒙特卡洛仿真实验。先设置信噪比为0 dB、5 dB、10 dB、15 dB、20 dB、25 dB,再在各个信噪比下生成100张DTMB循环谱等高图以及100张目标回波信号循环谱等高图,然后按照上述检测流程,统计各个信噪比下,检测出有无人机出现的概率,最后画出检测概率图。图6仿真结果证明了该检测方法的有效性,同时不需要复杂的信号处理也能达到检测无人机微动特征的目的,与其他无人机检测算法相比,降低了检测难度。
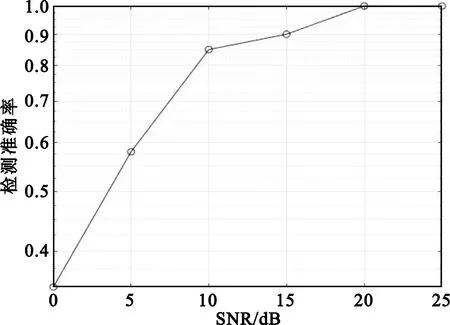
图6 检测概率图
3 实测验证
3.1 实测方案与配置
实验场景配置如图7所示,接收站位于桂林电子科技大学图书馆五楼的阳台,接收装置的控制中心为FPGA,采样芯片为AD9361,采样带宽为40 MHz,中心频率为603 MHz。发射站为尧山广播电视塔,选择的DTMB参数如表1所示,属于V频段,频道为DS-26,频带范围为614~622 MHz,中心频率为618 MHz。图7左上角为实验所用的大疆精灵4pro无人机,参数如表2所示,微多普勒频率为fv=60 Hz。实验中为充分考察旋转叶片的微多普勒效应,将该无人机悬停于信号采集装置前方32 m,距装置高度30 m处采集数据,此时悬停状态下的无人机主体多普勒频率可忽略不计。AD9361先通过混频器将广播信号转换成固定的中频信号,然后,正交解调器再将中频信号向下转换成复基带信号,在复基带处信号被采样频率为40 MHz的ADC传递到数字处理器。接着,通过千兆网口将硬件采集平台的信号上传到电脑中,电脑通过上位机软件将信号存储为I、Q两路数据。最后,通过Matlab仿真软件进行数据处理。

图7 微多普勒特征信号探测实验场景
3.2 实测结果分析
利用低通滤波器对实测信号进行杂波滤出后,得到图8所示的实验结果。
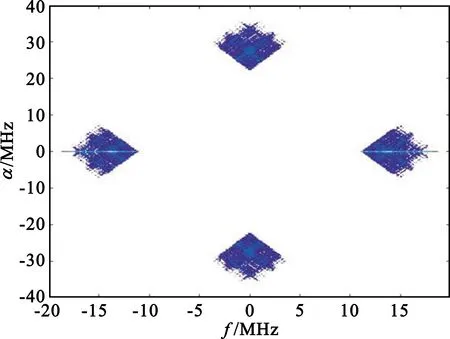
(a)直达波的循环谱等高图
其中,图8(a)的总灰度值为57 732 556,图8(b)的总灰度值为57 886 529,直达波和目标回波的循环谱等高图之间区别明显,并且通过检测流程,判断出有无人机出现,达到了检测无人机的目的。循环谱等高图中除了信号特征信息外,几乎80%的区域是空白的,为后续的图像识别带来了良好的稀疏特性。
4 结束语
本文在基于无源雷达探测的基础上,建立无人机微多普勒特征信号检测模型,分析了微多普勒特征在循环谱上的表现形式,并给出了一种针对无人机微多普勒特征的存在性检测算法。对该算法进行了仿真验证和实验测试,实验结果证明了算法的可行性。但对于多无人机情况下微多普勒特征是否会相互干扰甚至被掩盖的问题,本文还未进行深入研究。后续会对各种干扰情况进行研究。

