区域干旱重现期反演研究
徐 敏
( 辽宁省本溪水文局,辽宁 本溪 117000)
干旱频率分析是干旱风险划分的重要基础和内容,对干旱风险普查至关重要[1],也是对干旱发生和影响程度的重要评定依据,干旱重现期通过干旱频率反演,对干旱条件下水资源高效利用具有重要的意义[2]。早期干旱事件主要是针对区域内干旱发生及持续的时空特征上进行单维变化分析[3- 5]。为了解决单一维度干旱变量不能有效反演干旱迁移变化规律的问题,基于干旱强度、持续时间、间隔时段等多变量的干旱频率分析得到一定程度的研究[6- 9]。在这些成果中,Copula函数可克服传统单变量分析方法的不足[11],在国内一些地区干旱频率分析中得到应用和推广[10- 12]。近些年来。受人类活动和气候变化的综合影响。阜新地区近些年来发生严重干旱事件的频次逐年增高,且存在多发频发的演变态势[15]。为有效应对区域干旱变化,制定有效的抗旱措施,将传统被动抗旱转为主动防御旱情,需要对干旱发生频率及干旱风险进行综合分析。为此本文基于Copula函数,以干旱特征两个重要影响指标为依据,建立其联合概率模型,对区域干旱重现期进行重构反演分析。研究成果对于阜新地区干旱演变特征以及干旱风险具有重要的参考意义。
1 干旱重现期计算方法
结合干旱历时和干旱烈度双变量联合概率以及各单量概率可分析,干旱历时和干旱烈度分别大于d和s时,或者其同时大于d和s时的干旱频率计算方程为:
P(D>d)=1-P(D≤d)=1-FD(d)P(S>s)=1-P(S≤s)=1-FS(s)P(D>d,S>s)=1-FD(d)-FS(s)+FD,S(d,s)
(1)
式中,P—干旱频率;FD—干旱历时累积概率分布函数;FS—干旱烈度累积概率分布函数;FD,s—干旱烈度和干旱历时累积概率分布函数;D—干旱历时统计变量,d;S—干旱烈度统计变量;d—发生某一程度干旱事件的干旱历时,d;s—发生某一程度干旱事件的干旱烈度。
一年中干旱事件可能发生1次,也可能多次发生,因此干旱重现期分析不适合采用设计洪水重现期的计算方法。干旱历时D和干旱强度S大于或等于某一数值的重现期为:
TD=T(D≥d)=E(L)/P(D>d)Ts=T(S≥s)=E(L)/P(S≥s)
(2)
式中,TD—干旱历时重现期,d;Ts—干旱强度重现期,d;E(L)—干旱持续时间与未发生干旱历时的两个干旱特征变量期望值相加,d。
干旱重现期的计算以同时表征干旱烈度和干旱历时的可能度,与单变量重现期计算方法不完全等同。干旱烈度和干旱历时同时考虑时其干旱重现期TDs计算方程为:
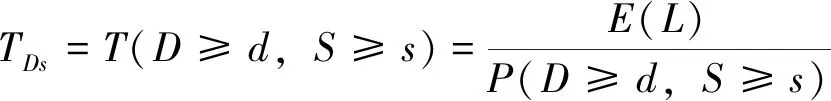
(3)
方程中,TDs—干旱历时和干旱强度联合分布的重现期,d;T—重现期,d。
2 旱评估指标选取
分别选用降水距平百分率Pa、标准化降水指数SPI和Z指数作为干旱评估指标,对阜新地区干旱指标适用性进行评估。各干旱指标时间计算尺度为1个月。阜新地区各县区干旱指标识别结果见表1。
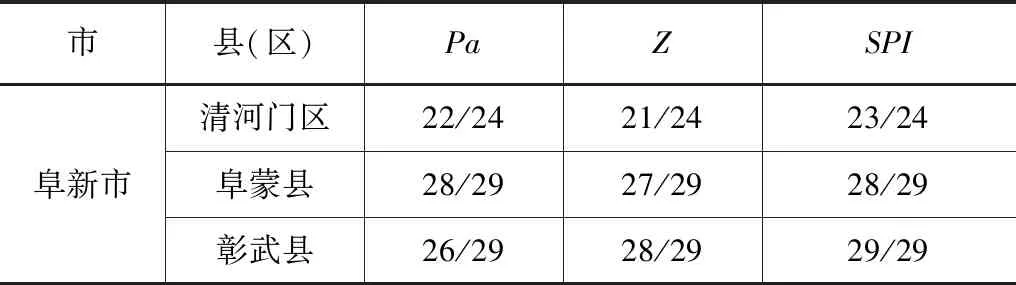
表1 阜新市各县区干旱指标识别结果对比
由表1可见,对于各县区来说,1个月尺度的SPI、Pa以及Z指数的干旱识别结果各有不同,其中SPI在月尺度干旱识别误差均可低于5%,具有较好的识别精度。为此,将1个月尺度的SPI作为研究区域干旱事件识别指标,并据此进行干旱频率计算。
3 干旱特征变量提取
在区域干旱事件识别的基础上,对其干旱样本数据系列进行获取,对于符合干旱特征的变量样本序列需要进一步定量和客观表述。干旱历时和烈度可用来表征干旱特征变量。干旱历时是指某一场次干旱事件过程的持续时间,用于定量描述干旱事件的时间特征。依据游程理论,识别结果的横轴跨度即为干旱历时。干旱烈度是指某一场次干旱事件的累积水分亏缺程度,体现为阈值指标与干旱指标之差的累积和,用于定量描述干旱事件的严重程度。即下图历时干旱指标SPI与阈值之差的累积值来计算。阜新地区干旱事件识别结果见表2,并基于1个月尺度SPI对阜新地区干旱特征便利进行系列统计,统计结果见表3。
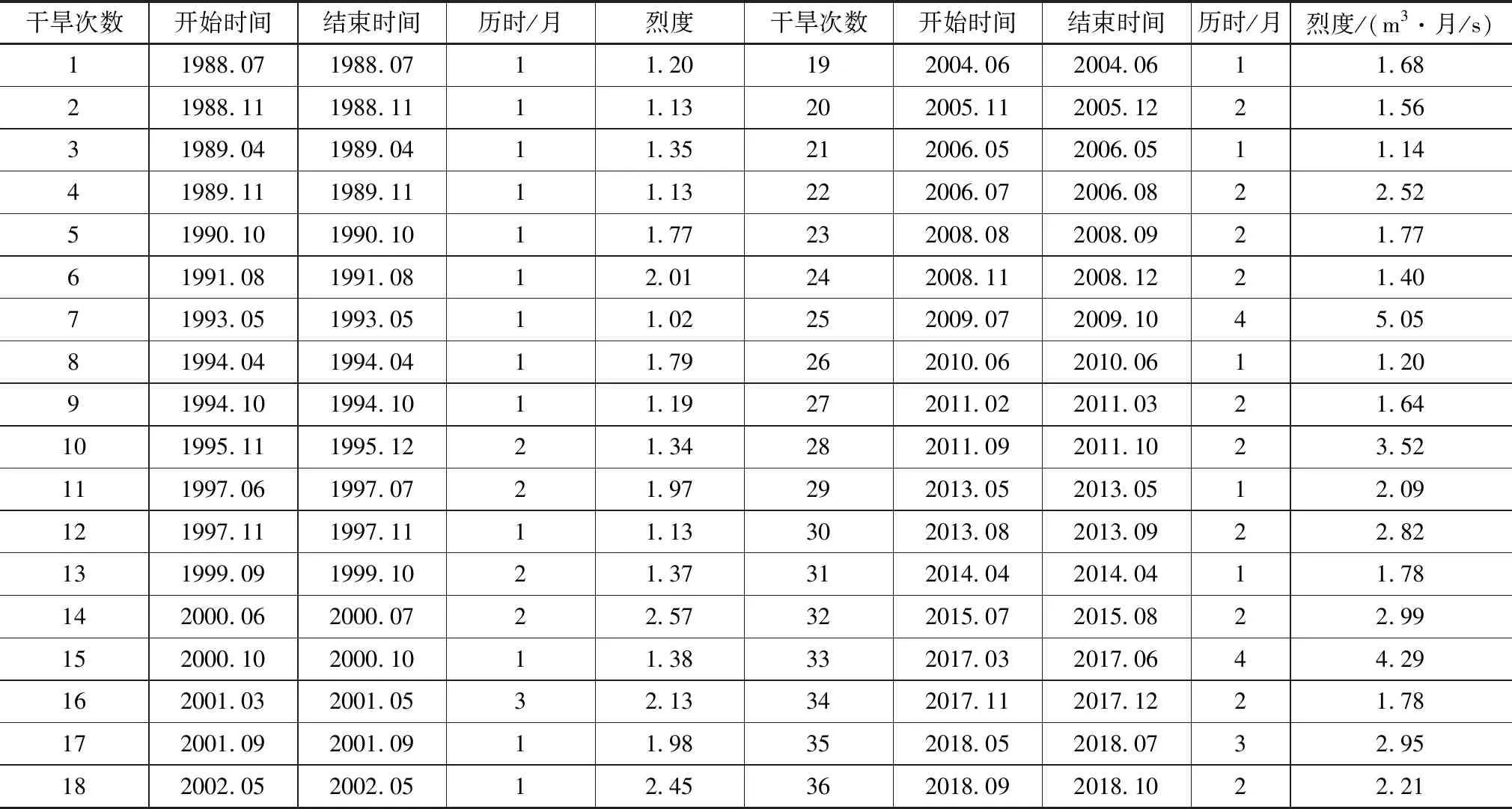
表2 阜新市干旱事件识别结果

表3 基于1个月尺度SPI指标的阜新地区干旱特征变量系列统计结果
基于表3阜新地区干旱特征变量系列统计结果分析可知,近30年间,基于1个月尺度SPI指标识别的阜新地区县区的干旱事件数在20~50次,与抗旱统计报表的数据相近。各县区平均干旱历时在6—9月之间,总的来彰武县和阜蒙县具有相对较长的干旱历时均值以及相对较大的干旱烈度均值,清河门区具有相对较短和相对较小的平均干旱历时和平均干旱烈度。
4 干旱特征变量特征变量联合频率分析
传统多变量概率分析模型假设具有相互独立的变量,各独立变量边缘概率相乘即为其联合分布概率,或者假设各变量边缘概率处于同分布,变量联合分布表达式为显式。但是由于干旱烈度和干旱历时之间存在显著关联性,且变量概率分布均不相同,因此需要采用不同类型概率分布函数进行联合概率分布分析。为此本文结合Copula多函数,基于阜新地区干旱历时和干旱烈度分析数据作为干旱特征双变量进行干旱联合频率分析,分析结果见表4,并对其联合概率分布进行了分析,如图1所示。
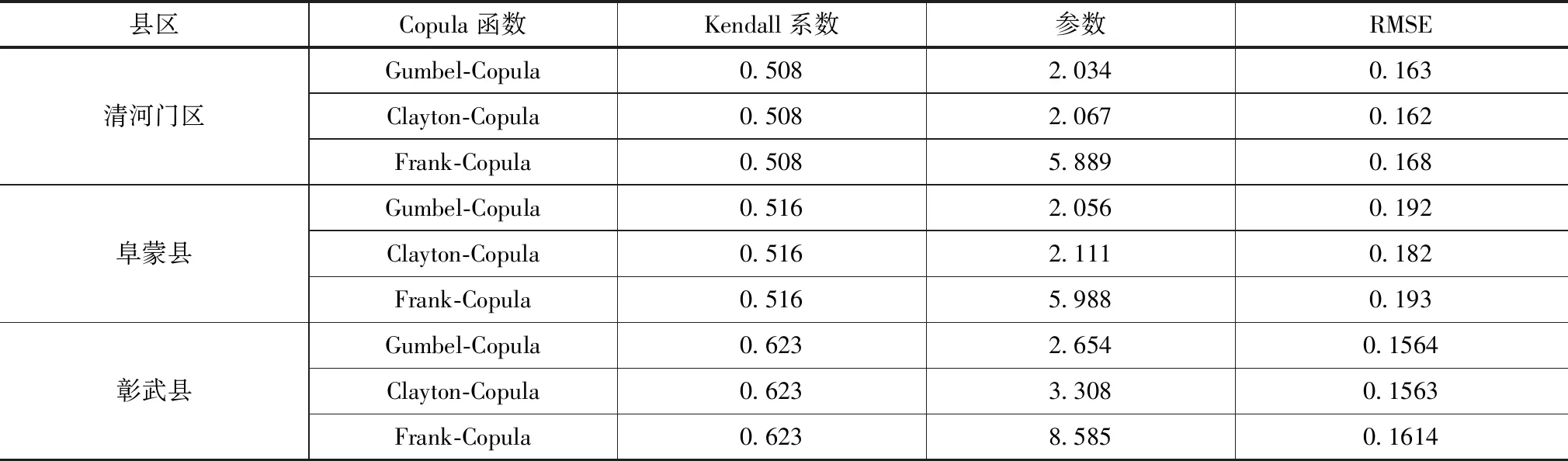
表4 基于RMSE的Copula函数最优选择
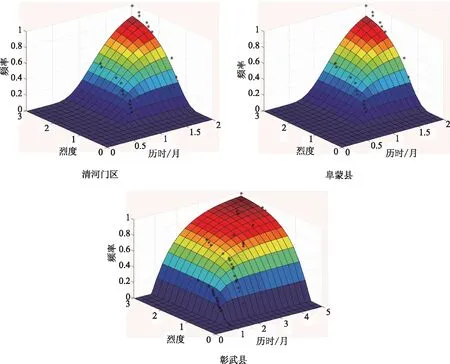
图1 阜新县区干旱联合概率分布曲线
从分析结果可看出,清河门区不同类型干旱联合概率分布Copula函数的Kendall相关系数均高于0.5,Clayton-Copula的均方根误差RMSE值在各类型函数中最低,为0.162,其拟合结果也优于其他函数,相比于其他两类函数更适合于清河区干旱联合频率分布特征,其联合干旱频率分布函数为
式中,C—干旱频率分布函数;cl、μ、ν、θ—函数参数。
阜蒙县不同类型干旱联合概率分布Copula函数的Kendall相关系数也均高于0.5,总体而言Clayton-Copula函数的方根误差RMSE值在各类型函数中最低,拟合度更好,其函数为
从彰武县各类型分布函数的Kendall相关系数可看出,其相关系数高于0.6,Clayton-Copula函数拟合度最高,方根误差RMSE值最低,其分布函数为
从阜新地区干旱联合概率分布函数可看出,Clayton-Copula为该区域干旱频率最优概率分布函数。
5 干旱重现期分析
通过对干旱及烈度联合频率的分析,计算得到阜新地区的干旱重现期,结果见表5。

表5 阜新地区的干旱重现期分析结果
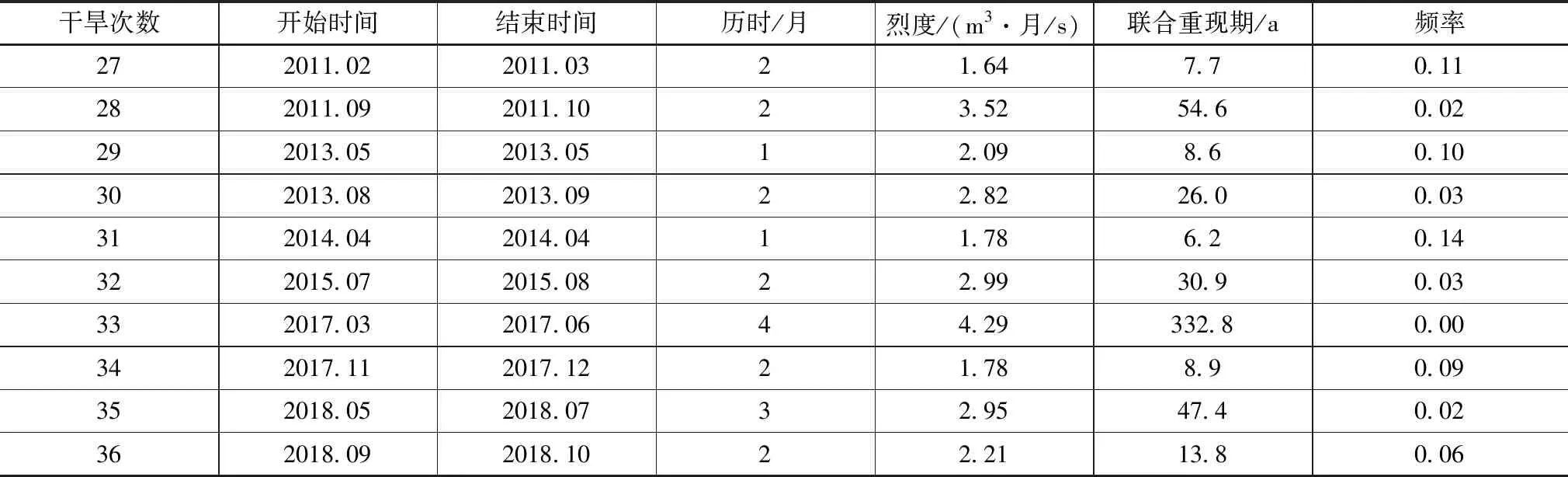
(续表5)
干旱重现期主要表示在长时段内每平均出现一次超过或等于某一量级干旱事件所间隔的历时,一般以年为计算时间。干旱重现期和干旱频率存在定量联系。干旱重现期相比于干旱频率可综合反映干旱事件随机性更便于抗旱减灾实际工作中发布具体旱情信息。此外需要说明的是如百年一遇干旱不应被认为相隔100年出现一次干旱事件,这种干旱量级从概率论角度出发其在100年内出现的频次可能超过1次,也可能出现的频次为0。
6 主要结论
(1)在Copula三种主要类型函数中,Clayton-Copula函数拟合结果最优,因此在采用Copula函数进行干旱历时-烈度干旱联合概率分析时,建议主选Clayton-Copula函数作为其拟合函数。
(2)在进行干旱事件指标识别时,为更好的反演区域干旱变化特征,建议以不同干旱指标识别误差低于5%为控制指标,选取误差较低的指标进行干旱事件识别。
(3)干旱重现期和干旱频率存在相互对应关系。干旱重现期相比于干旱频率可综合反映干旱事件随机性,相比于干旱频率更适合于抗旱减灾实际工作中具体旱情信息的发布。

