钢覆面矫形工装上矫形架结构优化分析
王仓平
(中国核工业二三建设有限公司,北京 100000)
核环保项目的钢覆面包含热室钢覆面、设备室钢覆面和不锈钢水池覆面。钢覆面的加工具有施工体量大、焊接点多、土建安装深度交叉施工作业等特点[1]。根据设计技术要求,钢覆面安装要先制作焊接龙骨,由焊接龙骨支撑钢覆面板材,钢覆面的支架龙骨焊接点多,焊接由于受局部热点影响,大尺寸焊接极易出现扭曲变形和波浪变形,受焊缝布局不规则,焊接变形难以控制,大尺寸预埋龙骨焊接矫形,在行业内的焊接件安装施工作业中都属难点。为保证施工进度,方便现场使用,项目部研发了钢覆面施工专用矫形工装。矫形工装的结构如图1所示。其中上矫形架对整个矫形工装起着至关重要的作用。但由于上矫形架横梁跨度大,在施工过程中附加载荷时会产生变形,影响矫形件的最终矫形结果。因此很有必要对上矫形架进行有限元分析,对其结构进行优化设计。

图1 矫形工装结构示意图
矫形工装的上矫形架为横梁结构,罗传林[2]等人对龙门式机床横梁的板筋结构形式、截面形状、导轨分布形式作了研究分析,用有限元分析方法,对不同截面形状的横梁在特定方向的刚度大小进行了分析对比。郭铁能等[3]建立了横梁力学模型和有限元数学模型,采用ADAMS 和ANSYS 进行了仿真研究,定量地得到横梁各导轨面承载时的变形。通过对仿真数据的分析,确定了横梁导轨面变形的承载曲线和曲线方程;许丹等[4]采用机械系统多刚体动力学仿真软件ADAMS 和有限元分析软件ANSYS对横梁进行了静动态特性分析,计算出考虑重力和切削力作用下横梁部件的静态变形,以及通过动态测试和参数辨识方法,获得导轨结合面特性参数。最终经过模态分析得到系统固有频率和各阶振型图;侯红玲等[5]利用有限元分析软件ANSYS 在材料和截面空间尺寸相似的情况下,对截面形状不同的几种结构的梁进行静力和模态分析,将强度较好的梁,用模态分析得到刚度更好的梁。通过结构的变形和一阶频率的振型研究比较,最终确定了较为合理的横梁结构。
通过文献可以看出,横梁的应力分布、形变位移等情况对工装的整体精度和性能有着很大的影响,对矫形工装的上矫形架横梁进行有限元分析及优化设计显得尤为重要。本文通过对研发的矫形工装上矫形架进行有限元分析和优化设计,以提高矫形工装的作业精度。
1 矫形工装上矫形架模型简介
上矫形架的结构和受力时的形变量对工装整体矫形精度有很大的影响。如图2 所示,上矫形架分别由两侧的脚柱和上部的横梁,以及附属构件千斤顶、用于连接千斤顶和横梁的支架板和有安装在脚柱上的行走机构组成,横梁材料为工字钢。

图2 上矫形架结构示意图
为分析横梁的应力分布和承受载荷时的应力分布情况,我们选取横梁、脚柱和支架板受力部分为研究对象。建立如图3 所示的坐标系,其中横梁长为l,千斤顶和支架板上装有滚轮可在横梁上来回移动以保证加工需求。千斤顶安装位置即为载荷施加位置,我们分别选取横梁的2 等分点、3 等分点和4 等分点进行计算。施加总力为7000N。

图3 选取的研究模型
横梁和脚柱材料为Q345B。材料力学特性参数见表1。

表1 材料特性参数
2 数值模型建立
2.1 上矫形架的有限元模型
对Solidworks 建立的上矫形架三维模型进行网格划分,并设置其材料属性和边界载荷。最小单元尺寸为3mm,2 等分点模型、3 等分点模型和4 等分点模型到达离散模型的单元数分别为2175771、2187137 和2185661。以2 等分点模型为例,离散后的上矫形架有限元模型如图4 所示。

图4 吊装梁有限元模型
2.2 有限元模型约束条件
根据实际约束情况,边界条件设置如下:
1)两脚柱底端设置为固定约束;
2)支架板下底面设置有垂直向上且均匀分布的载荷,总力大小为7000N。即f2=-7000N,且2 等分点模型仅中间位置设置有一个受力点,3 等分点和4等分点模型中分别布置有两个受力点。
3 计算结果
3.1 上矫形架应力分析
上矫形架的等效应力分布和形变量分别如图5所示。变形位移量按照100 倍放大显示。

图5 各模型应力分布(单位:Pa)
计算得当附加载荷f2=-7000N 时,2 等分点、3等分点和4 等分点各模型的最大等效应力值分别为302MPa、266MPa 和226MPa,满足材料的屈服强度。从图5 可以看出最大等效应力发生在横梁与脚注连接部分,横梁的最大等效应力发生在横梁的中间位置。且施加的载荷越靠近横梁两端,最大等效应力越小。特别是当受力点处于横梁中间部位时,最大等效应力302MPa 接近材料屈服强度,对矫形件进行矫形作业时,当施加的力大于7000N 则最大等效应力很有可能超过材料的屈服极限。应此,在矫形工装矫形作业时应最大可能的避免载荷集中分布在横梁中间位置。
3.2 上矫形架变形分析
上矫形架横梁各处的形变量如图6 所示。

图6 各模型横梁各处形变量
从图5 可以看出当附加载荷f2=-7000N 时,2等分点、3 等分点和4 等分点各模型的最大形变量分别为3.16mm、2.63mm 和2.1mm,各模型的最大形变量均位于横梁中点处。结合应力分析,有必要对上矫形架结构进行优化,以提高矫形工装可靠性和作业精度。
4 上矫形架优化分析
4.1 模型优化
为满足上矫形架作业精度和可靠性,对上矫形架进行优化设计,以3 等分点受力为例,优化后的模型如图7 所示。
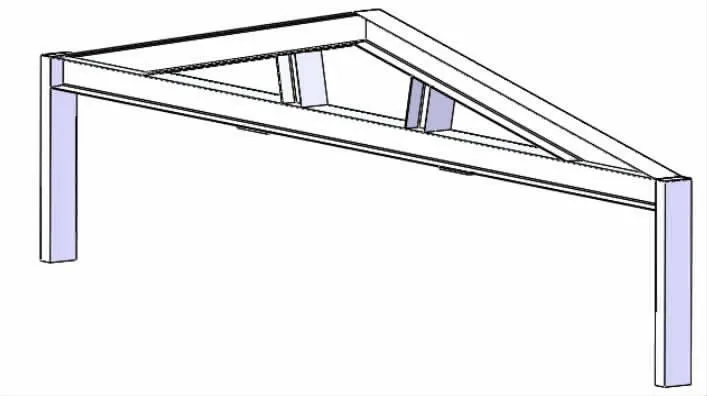
图7 优化模型示意图
4.2 优化模型计算结果
对优化后的模型进行网格划分,再进行数值计算,约束条件和边界条件设置与2.2 一节所述相同。计算得应力分布和横梁各处位移结果分别如图8、图9 所示。
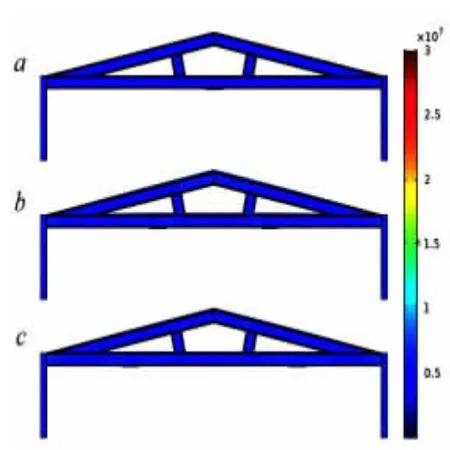
图8 各模型应力分布(单位:Pa)

图9 横梁各处形变量
对优化模型计算得当附加载荷f2=-7000N 时,2等分点模型、3 等分点模型和4 等分点模型各自最大等效应力值分别为3.15MPa、50MPa 和46MPa,三者均满足材料的屈服强度。相比优化前,各模型最大等效应力分别减小了98.96%、81.2%和79.64%,相同载荷下的应力优化效果明显。2 等分点、3 等分点和4 等分点各模型的最大形变量分别为0.02mm、0.32mm 和0.26mm,各模型的最大形变量均位于横梁中间段,相比优化前分别减小了99.37%、87.83%和87.61%。大幅度提高了矫形工装的作业精度。
5 结论
本文通过对矫形工装的上矫形架进行数值模拟,得到了上矫形架施加载荷f2=-7000N 时的等效应力分布情况和应变情况。在数值结果的基础上对原有的矫形工装进行了优化设计,并对优化后的上矫形架进行数值分析,最终结果如下:
1)优化前,上矫形架施加载荷f2=-7000N 时,各模型最大等效应力均位于横梁与脚柱连接处,横梁上的最大应力位于横梁重点处,且最大等效应力都满足材料屈服强度。且施加的力越靠近横梁两端,最大等效应力越小。
2)当在上矫形架的中间位置施加7000N 的载荷时,最大等效应力接近材料屈服强度。作业时在满足作业要求的前提下应避免此类情况发生。
3)上矫形架的优化效果明显,2 等分点模型、3等分点模型和4 等分点模型的最大等效应力分别减小了98.96%、81.2%和79.64%。在作业时,优化后的矫形工装可承受更大的载荷。
4)优化后的2 等分点模型、3 等分点模型和4等分点模型的最大形变位于分别减小了99.37%、87.83%和87.61%,比结构优化前,相同载荷下,横梁的应变减小,有助于提高作业精度。

