A Numerical Convex Lens for the State-Discretized Modeling and Simulation of Megawatt Power Electronics Systems as Generalized Hybrid Systems

Bochen Shi, Zhengming Zhao*, Yicheng Zhu, Zhujun Yu, Jiahe Ju

Department of Electrical Engineering, Tsinghua University, Beijing 100084, China

Keywords:Generalized hybrid systems Megawatt power electronics Modeling and simulation Numerical convex lens

ABSTRACT Modeling and simulation have emerged as an indispensable approach to create numerical experiment platforms and study engineering systems.However,the increasingly complicated systems that engineers face today dramatically challenge state-of-the-art modeling and simulation approaches. Such complicated systems,which are composed of not only continuous states but also discrete events,and which contain complex dynamics across multiple timescales, are defined as generalized hybrid systems (GHSs) in this paper. As a representative GHS, megawatt power electronics (MPE) systems have been largely integrated into the modern power grid, but MPE simulation remains a bottleneck due to its unacceptable time cost and poor convergence.To address this challenge,this paper proposes the numerical convex lens approach to achieve state-discretized modeling and simulation of GHSs. This approach transforms conventional time-discretized passive simulations designed for pure-continuous systems into state-discretized selective simulations designed for GHSs.When this approach was applied to a largescale MPE-based renewable energy system, a 1000-fold increase in simulation speed was achieved, in comparison with existing software.Furthermore,the proposed approach uniquely enables the switching transient simulation of a largescale megawatt system with high accuracy, compared with experimental results,and with no convergence concerns.The numerical convex lens approach leads to the highly efficient simulation of intricate GHSs across multiple timescales, and thus significantly extends engineers’capability to study systems with numerical experiments.

* Corresponding author.

E-mail address: zhaozm@mail.tsinghua.edu.cn (Z. Zhao).

https://doi.org/10.1016/j.eng.2021.07.011

2095-8099/© 2021 THE AUTHORS. Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1. Introduction

With the rapid development of computational technologies in recent decades,numerical modeling and simulation have emerged as an indispensable approach to recreate,explore,decode,and predict complex dynamics of interest across a wide range of scientific disciplines and engineering applications [1,2]. However, with the rapid development of science, technology, and modern society,the dynamic behavior of the physical systems of interest to humanity is becoming increasingly complicated, such that these systems can no longer be simply regarded as pure-continuous systems [3,4]. The emergence of such complicated systems dramatically challenges state-of-the-art modeling and simulation approaches.

Fig.1 provides some examples.In ecosystems(Fig.1(a)),events such as crustal movement, volcanic eruption, and glacial melting fundamentally change the evolution mode of the system, particularly when taking into account climate change due to recent human activities [5,6]. Another example is the spread and control of coronavirus disease 2019 (COVID-19) as shown in Fig. 1(b), in which control measures such as travel bans and city shutdowns changed from time to time according to the spread of infection,and in turn governed the spread pattern of the disease [7,8]. Engineering examples include chemical processing plants, in which continuous states such as temperature interact with discrete events such as phase transition[9].In robot control,foot impacting and knee locking lead to mode transitions [10]. Clearly, the above systems cannot simply be modeled as pure-continuous systems.They show a hybrid nature involving the coexistence of both continuous states and discrete events.

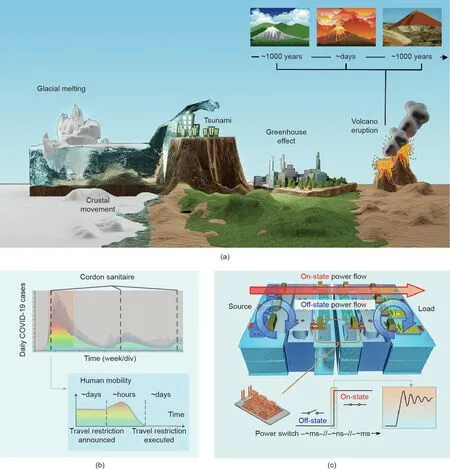
Fig. 1. Typical examples of generalized hybrid systems (GHSs) and their multi-timescale nature. (a) Discrete events in an ecosystem fundamentally change the evolution mode(e.g.,biodiversity).The timescale of these events is relatively very small.(b)Control measures for COVID-19 as discrete events change the infection modes of the virus as continuous states.Peak mobility may occur during the short period of the discrete event(e.g.,after the announcement and before its execution).‘‘Week/div”refers to the unit of the x-axis is one week per grid. (c) In power converters, switching events of the semiconductor switches control the transfer of energy flow as desired. The nanosecond-level switching transient causes an abrupt change of electromagnetic energy and, sometimes, system failure, especially in megawatt power electronics (MPE)systems.

Another engineering example that we focus on in this paper is that of power electronics systems (Fig. 1(c)). Power electronics have been widely used in nearly all electric energy conversion fields [11]. In particular, given the increasing concerns about climate change and the energy crisis, megawatt power electronics(MPE) systems act as indispensable interfaces to connect renewable sources with the utility grid and end users[12].In power electronics converters, the originally continuous voltage and current are‘‘discretized”through the introduction of power semiconductor switches [13]. Hence, the system demonstrates the coexistence of both continuous states and discrete events, and can thus be defined as a hybrid system.

The term ‘‘hybrid system” originated from a special workshop that was held in 1986 [14], and soon became an emerging topic[4,15,16].The early defined hybrid system mainly involved continuous states controlled by discrete signals [17]. Thus far, the concept has been enormously expanded to include the mixing of and interaction between continuous states and discrete events[15]. However, the abovementioned definitions and discussions still cannot depict the full complexity of the hybrid nature of engineering systems today.On many occasions,discrete events cannot occur instantaneously.It is known that time is the measurement of existence; therefore, there must be a time interval during the‘‘event,”although it is often too fast to be perceived.From a physical perspective, a discrete event still has a continuous transient with a small timescale; this results in a prominent multitimescale feature in generalized hybrid systems (GHSs) (Fig. 1).The transients of discrete events can have great significance,especially when the physical energy during the short transient of an event is large [18]. A typical example is the switching transient in MPE (Fig. 1(c)). Because the power level is high, the ‘‘sudden change”and‘‘imbalance”in large electromagnetic energy is highly likely to cause system faults [19–21].

These switching transients cannot be described within the conventional concept of a hybrid system and the ideal concept of a discrete event without any physical process. Therefore, in this paper,we introduce and define the concept of a GHS in order to describe a more general and complete context of the hybrid nature of physical systems. We define a GHS as follows: A GHS is a multitimescale dynamic system composed of both time-driven continuous dynamics and event-driven discrete dynamics, where largetimescale continuous dynamics embody discrete processes, and discrete processes embody small-timescale continuous transients.

In GHSs, continuous states and discrete events as two distinct types of variables co-exist and interact with each other, collaboratively determining the system behavior. Meanwhile, two types of continuous states of different timescales simultaneously exist within the system, resulting in a prominent multi-timescale feature that must be considered in high-power applications. Such GHS are not only commonly found in the physical world, but also regarded as a more general form of the dynamic system.Subsequently,a challenge of such a complicated dynamic behavior—which is of equal significance to many engineers in various applications—is the effective and efficient modeling and simulation of GHSs.

The remainder of this paper is organized as follows: The challenges of modeling and simulating GHSs using conventional approaches are summarized in Section 2. A so-called ‘‘numerical convex lens” designed based on the features of a GHS in order to achieve state-discretized modeling and simulation is then proposed in Section 3 to address these challenges. The proposed approach has general value for different GHSs in various engineering applications. More specifically, we examine how to model and simulate an MPE system as a representative GHS. Applications of the proposed approach in MPE systems are demonstrated in Section 4. Finally, conclusions are drawn in Section 5.

2. Challenges of modeling and simulating GHSs

2.1. Modeling and simulation challenges for general GHSs

In current modeling and simulation approaches [22], time is taken as the independent variable to build the system model and determine the corresponding solver; this is called the timediscretized approach. This approach is a natural idea: Since time is the measurement of existence, to study a dynamic system is to explore the pattern of the system dynamics based on time. However, time flows continuously and uniformly without qualitative change. In contrast, the variables of state in GHSs can not only accumulate, but also change qualitatively. In other words, when a certain condition is fulfilled, the system will switch to another mode and continue its accumulation under a totally different pattern. In this situation, numerical experiments based on timediscretization encounter a significant challenge: The discretized timepoints may not be the exact time when an event occurs.Therefore,such experiments are incapable of evaluating the event’s impact on the system dynamics accurately. As a consequence, an extremely small timestep must be adopted in order to accurately locate the discrete event and solve the corresponding smalltimescale transient during the event,which results in dramatically low efficiency, or even computational failure.

2.2. Challenges of modeling and simulation for MPE systems

The subsection above provided a general discussion of the challenges encountered when modeling and simulating GHSs. We now discuss MPE systems in detail in order to demonstrate more concrete examples.The modeling of MPE systems can be basically categorized into three types according to different levels of semiconductor models:average models [23,24], ideal models [25–27], and physical models[28–30]. The average model eliminates (averages) the switching actions within one or several switching cycles and therefore transforms the GHS into a pure-continuous system. Thus, the analyses and designs of the system—especially those of the closed-loop controls—can be well-supported with available mathematical tools such as the transfer function and the bode plot [31]. Within the context of GHSs,the average model only focuses on the large-timescale continuous dynamics. The impact of discrete events is ignored, let alone switching transients within the events.When considering the switching events, the ideal switch model is widely used in many systemlevel simulation tools [26]. This model considers the ‘‘largetimescale continuous–discrete”process,but still ignores the switching transients of switching events.

Existing models of switching transients are complicated equivalent circuits based on semiconductor physics, as shown in Fig. 2[28]. Such physical models abandon the assumption of discrete events and describe the semiconductor switches as smalltimescale continuous systems instead. The GHS is then transformed again into a pure-continuous system, but this time into a small-timescale system that considers the switching transients.Theoretically, physical models accurately describe smalltimescale transients. Practically, these physical models have also been implemented in device-level commercial tools for power electronics [29,32] and have been used in studies with a small number of switches. Unfortunately, it is hardly possible to use them in MPE applications, in which typically hundreds or thousands of semiconductor devices exist and interact with each other[33,34].An example is the simulation of a 24-switch 50 kVA solidstate transformer with physical switch models tested in Ref. [35];although it is just a medium-scale circuit, the simulation already takes about 9 h and frequently encounters divergence failures during numerical studies.It is scarcely possible to simulate larger converters in MPE simulations with physical models within an acceptable time period while ensuring a convergent result.

To sum up, it is still challenging to model the integral‘‘continuous–discrete–continuous” process in MPE. Existing approaches are still based on time as the variable to develop the models; therefore, only a certain aspect (i.e., continuous/discrete)and certain timescales can be focused on.

The solving of MPE systems as GHSs is equally challenging due to the enormous number of switching events.Existing approaches such as state-space methods [26,27] and nodal analysis methods [36],which are equipped with various fixed- or variable-step integration methods[37],still fall under the category of time-discretized solvers.Such methods are incapable of automatically matching discretized points with the occurrence of discrete events and,furthermore,with the small-timescale transients within the events, which are fundamental features introduced by GHSs.Iterations are frequently necessary during the simulation in order to locate the discrete event, and small timesteps must be adopted to solve the transients and overcome convergence issues, as shown in Fig. 3. For MPE systems with hundreds or thousands of semiconductor switches, the switching events of different switches are typically asynchronous. Even for a relatively low switching frequency, such as 1 kHz, 1000 switches in the simulated system can cause events to occur 1 million times per second. This results in low simulation speed and poor convergence.

3. A numerical convex lens for state-discretized modeling and simulation

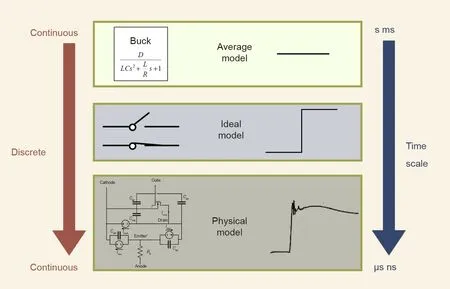
Fig. 2. Existing modeling approaches for MPE systems include the average model, ideal model, and physical model. Each model focuses on one aspect of the ‘‘continuous–discrete–continuous” process of the GHS,and the models vary from large to small timescales. For the average model,D is the duty cycle, and L,C, and R are the inductance,capacitance,and resistance in a buck converter,respectively.For the physical model,Cgs,Cgd,and Cdsj are the metal-oxide-semiconductor capacitances,Imult,Icss,and Ibss are the equivalent current sources in insulate gate bipolar transistor(IGBT),Ccer and Ceb are the equivalent capacitances in IGBT,Rb is the equivalent resistance connected to the anode, and Imos is the metal-oxide-semiconductor current.

To address the above challenges of modeling and simulation for GHSs, we propose the concept of state-discretized modeling and simulation.The general idea involves role-swapping the variable of time and the variable of state. In pure-continuous systems, time can be a sufficient variable to perform modeling and simulation.However,in GHSs,time is only a passive variable.Due to the introduction of discrete events and the corresponding small-timescale transients within the events, system states become a more dominating variable, which not only embodies the system dynamics,but also triggers the occurrence of events. By swapping the roles of time and state, a state-discretized solver can potentially merge the discretization of the simulation with the quantitative change of the GHS(i.e.,the occurrence of the events),and is therefore capable of modeling the integral process of multiple timescales while maximizing the simulation efficiency.

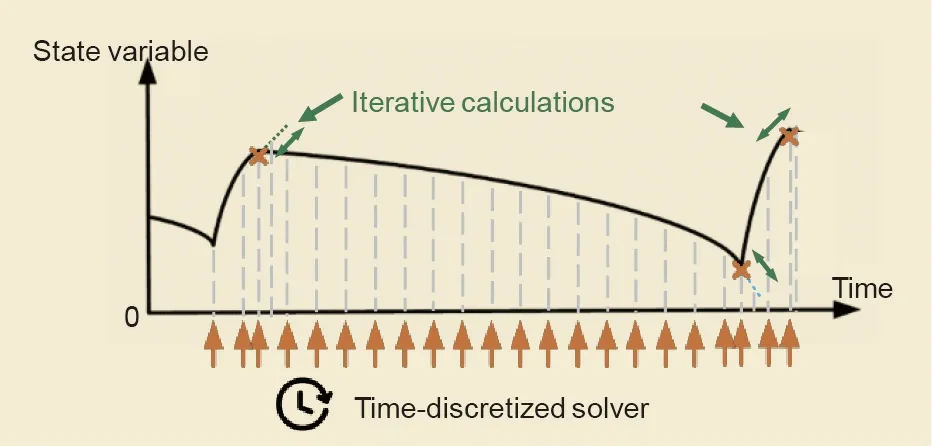
Fig. 3. Existing time-discretized solvers for MPE systems. Discretized points in a time-discretized solver can be mismatched with the occurrence of the discrete events.Iterative calculations are necessary to locate the events,and small timesteps must be adopted to simulate switching transients without convergence problems.

In this section, in order to implement the concept of statediscretized modeling and simulation, we receive inspiration from optics and propose a novel method called the ‘‘numerical convex lens.” Although they are considered to be two separate fields,optics and computational science share the same target: to perform observation,either with light or with computations.In optical experiments,if a certain part of an object cannot be clearly seen,a convex lens can be used to magnify it in detail.The degree to which the convex lens magnifies the observed object depends not only on the lens itself,but also on the incident rays from the object,such as their light frequency and intensity. This analogy inspired us to compare the system variables in numerical experiments(including continuous states and discrete events) to light rays and endow them with different ‘‘frequency” and ‘‘intensity,” so that they will have different refractive indexes through the numerical convex lens (i.e., the solver) and, therefore, different levels of magnification. In this way, we can pick out variables that have undergone qualitative changes (which means that their magnified images are clear enough to be observed) and let the clear imaging trigger the numerical experiment. This leads to a ‘‘selective” numerical observation, where we swap the roles of state and time. To be specific, with the help of the convex lens, the discretization of states(i.e.,the imaging process)triggers the solving of the system,and the discretization of time is determined accordingly. In this way, we can efficiently match the discretized solving points with the qualitative changes of system states without unnecessary calculations,which enables accurate and fast numerical experiments.

3.1. A fractal model of the GHS with the numerical convex lens

To perform numerical observation, the first task is numerical modeling. With the assistance of the numerical convex lens, we can establish a ‘‘fractal model” for GHSs (Fig. 4). In the fractal model, system dynamics are decoupled into different groups according to their differences in timescale, which are defined as different dynamic planes. The dynamics in the fast planes are the transient processes of discrete events in slow planes.In each plane,system dynamics can be modeled with the hybrid automaton model [25,38]. When observing the fractal model using the numerical convex lens, the system variables will be imaged through the lens. This process is called ‘‘state discretization.” The clear image triggers the numerical solving. In particular, when a discrete event occurs, the numerical convex lens will magnify it into a new dynamic plane and switch the numerical experiment into this plane, where the small-timescale behavior of the system is described as a new ‘‘small hybrid system.” When this discrete event ends, the numerical experiment will be switched back to the previous plane. In this way, the dynamics of different timescales can be decoupled,so that the solving speed and convergence of the numerical experiment can be simultaneously improved with high accuracy.The above idea is very similar to the idea of fractals in geometry:Research on fractal geometry has revealed that when observing the geometric features of a system on different spacescales, it is usually found that parts exhibit an amazing similarity to the whole; likewise, in numerical experiments, with the help of the numerical convex lens,we can observe the system dynamics in different timescales on different dynamic planes, and the dynamics on different planes can be similarly modeled as hybrid systems. Therefore, we call this numerical model of multitimescale GHSs the ‘‘fractal model.”

In the fractal model,system dynamics are decoupled into different groups according to their differences in timescale and defined as different dynamic planes. For example, as shown in Fig. 4, the system dynamics are divided into three groups and defined as three different dynamic planes: ①the slow dynamic plane containing second-to millisecond-scale dynamics;②the fast dynamic plane containing microsecond-to nanosecond-scale dynamics;and③ the ultra-fast dynamic plane containing picosecond- to femtosecond-scale dynamics. To observe the details in a discrete event in the slower plane, the numerical convex lens can be used to magnify the discrete event into a faster plane,which represents a small hybrid system. In other words, the dynamics in the fast planes are the switching transient of discrete events in the slow planes. If necessary, we can also magnify the switching transients in this small hybrid system into a dynamic plane with a ‘‘smaller timescale.”By repeating the above process,we can use the numerical convex lens to observe the dynamic behavior of the generalized dynamic system in different timescales on different dynamic planes.In this way,dynamics with different timescales can be distinguished, thus avoiding the need to consider unnecessary dynamic behaviors.

In each plane, the hybrid system can be modeled as a hybrid automaton [38], as illustrated in Fig. 5. The hybrid automaton model comprises the following elements:

(1) Variables

①Time variable t.

②State variables: A set of variables inside the system that can describe the dynamic behavior of the system completely and without redundancy.

Fig. 4. Establishing the fractal model of GHSs based on the numerical convex lens.GHSs exhibit prominent multi-timescale features. Based on the numerical convex lens, we can decouple the system dynamics into different groups and define them as different dynamic planes. Discrete events in each plane can be magnified and modeled as a new dynamic plane by the numerical convex lens.

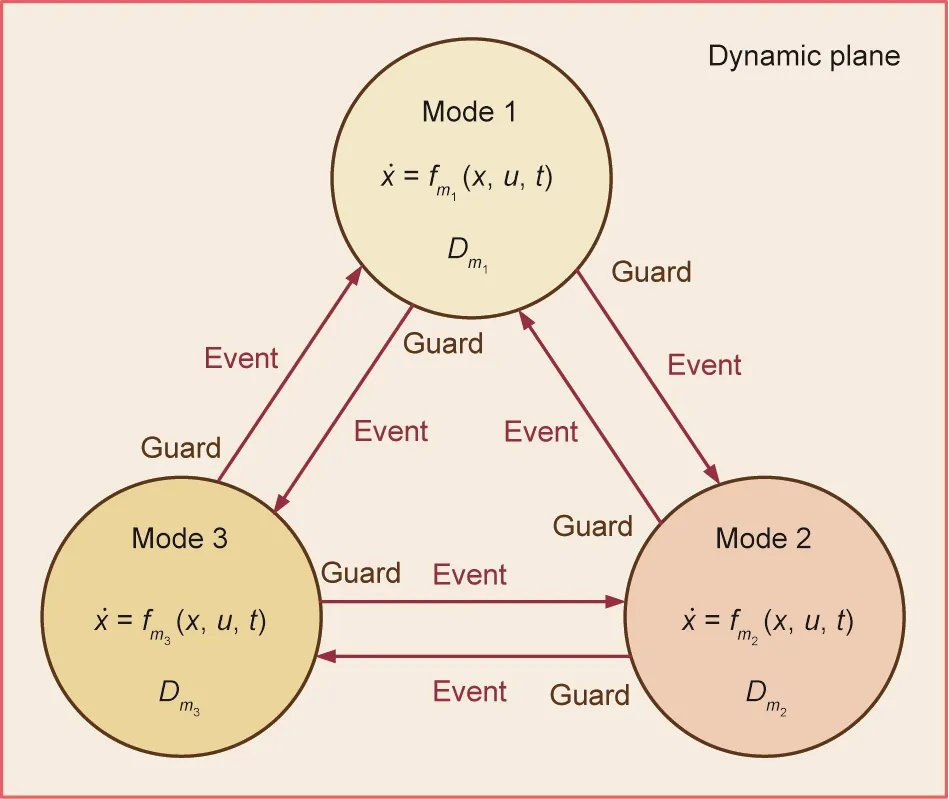
Fig. 5. The hybrid automaton model for a single dynamic plane. The model comprises four elements: variable, mode, guard, and event. A dynamic plane contains a set of all possible dynamic modes and guard conditions.

· Continuous state variables x: State variables that vary continuously with time.

· Discrete state variables d: State variables that vary discontinuously with time.

③Input variables u:Variables that are outside the system but can influence the dynamic behavior inside the system. Input variables can be continuous or discrete.

(2)Mode:The operating pattern of systems dynamics.A combination D of discrete variables dictates a mode. In different modes,the dynamic patterns are different, which means that the corresponding mathematical models are different. For example, in Fig. 5, for the kth mode mk, we can describe the system mode as the following ordinary differential equation (ODE):

where c is called the characteristic variable and can be expressed by state variables, and vthis the corresponding threshold value. When Eq. (2) holds true, system states will remain in the present mode.When the characteristic variable crosses the threshold,it will cause a change of the inequality’s Boolean value, and thus may trigger a mode transition of the hybrid system.

(4) Event: The mode transition of the hybrid system. An event happens when the guard condition of the present mode changes its Boolean value.

A dynamic plane contains a set of all possible dynamic modes and guard conditions.When a discrete event occurs and its transition details are of concern, the numerical convex lens can be utilized to magnify it and transfer the numerical experiment to the faster plane. When the transition process ends, an ending event will be triggered,and the numerical experiment can be transferred back to the slower plane.

3.2.State-discretized solving of a GHS with the numerical convex lens

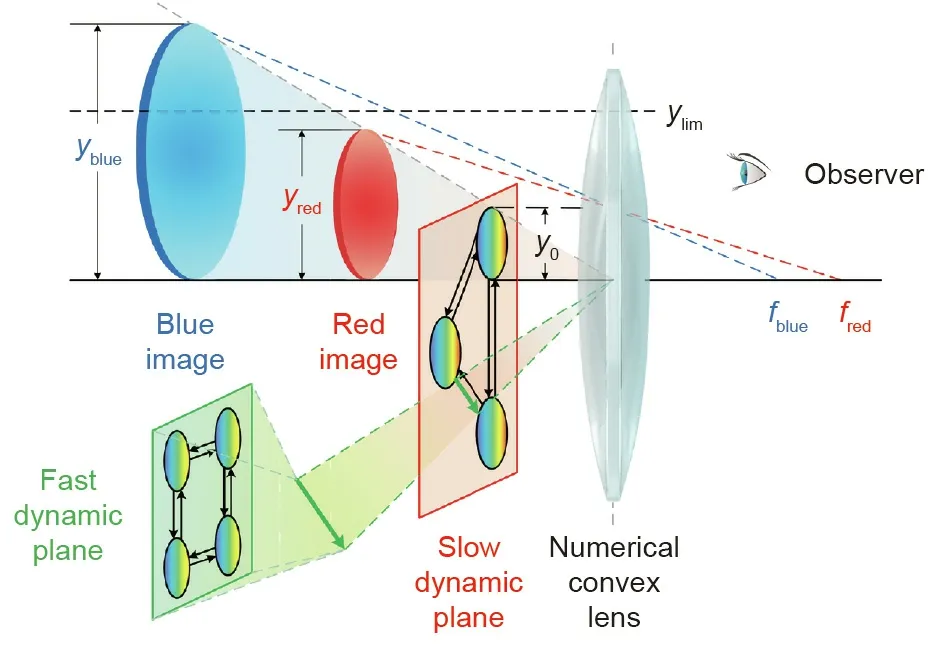
Fig. 6. Observing the fractal model of GHSs through the numerical convex lens.When solving the fractal model, the color(frequency) of the continuous states and the light intensity of the discrete events reflect the degree of attention that should be paid in the numerical experiment.They exhibit different refractive indices when they pass through the numerical convex lens,such that variables with a clear image,which are the variables that undergo qualitative changes, can be picked out to spontaneously trigger the numerical experiment. yblue and yred are the image heights of the blue and red light,respectively,and fblue and fred are the focal lengths of the blue and red light, respectively.

This section introduces how to solve the fractal model of GHSs.According to the principles of the numerical convex lens (Fig. 6),the system variables will separate into different light rays; hence,clearly imaged variables that have undergone qualitative changes will be picked out and will spontaneously trigger numerical experiments. In general, to solve a GHS composed of continuous states and discrete events,different imaging principles are used for these two categories of elements with different properties. Below are detailed descriptions on how to solve GHSs with the numerical convex lens.

Let u0be the object distance, y0be the object height, and y be the image height in Fig. 6. Let us assume that, in order to be captured by human eyes,the height of the image should be more than the resolution threshold ylim, that is,

Then the numerical criteria for clear image formation can be rewritten as

The remaining question becomes: What is the definition of the refractive index n for system variables? As was mentioned in the introduction of this paper,a GHS comprises two types of system variables: continuous states and discrete events. Since these two elements have different properties, their imaging principles in the numerical convex lens system are different.In the numerical system,we compare them to rays of light and endow continuous states with different colors (frequencies) and discrete events with different intensities. According to the refraction principle of the numerical convex lens,lights with different colors or intensities will have different refractive indices and different focal lengths, and their images will naturally be separated in space and have different sizes.

For continuous states,taking a single-variable case as an example,we compare it to a beam of monochromatic light with variable color,whose color at a certain moment corresponds to a frequency that is called the ‘‘numerical angular frequency.” Here, we define the numerical angular frequency as the measurement error in numerical experiments. At present, there have been many algorithms designed for pure-continuous systems that can provide the local error estimate at each timestep, such as the widely used ode45 algorithm[37]and others[39,40].Similar to the Cauchy dispersion formula in optics, the refractive index of the numerical convex lens for continuous states Δn1has the following nonlinear relationship with the numerical angular frequency ω:

where cbaseis the base value for the characteristic variable c. Eq.(10) shows that the closer the characteristic variable of a discrete event is to the threshold, the greater the weight of the discrete event will be, and the higher the priority it should be given in numerical experiments. Real lens materials can have nonlinearity and exhibit different refractive indexes for light with different intensities,in what is called the Kerr effect in optics.Inspired by this phenomenon, we endow the numerical convex lens with a similar effect and define the relationship between the refractive index Δn2and the light intensity as follows:

where K is the Kerr coefficient of the lens.The larger K is,the stronger the Kerr effect of the lens will be.Thus,K reflects another property of the lens,which represents the error tolerance of the solving of discrete events.

Taking the image formation principle of both continuous states and discrete events into account, we can obtain the complete expression of the refractive index, as follows:

For continuous states,we consider them to be variable-frequency and constant-intensity, and let KI ＜＜1; for discrete events, we consider them to be variable-intensity and constant-frequency,and let ω2/b2＜＜1. Based on the numerical criteria for clear image formation given by Eq.(8)and the complete expression of the refractive index given by Eq.(12),the fractal model can be solved according to the formed image of the system variables in the generalized hybrid system. Since the numerical convex lens can have both the dispersion effect and the Kerr effect, it has the ability to efficiently solve continuous states and discrete events at the same time.

3.3. Modeling and solving MPE systems

To apply the above-described general methods to the simulation of MPE systems,this subsection discusses detailed interpretations of all the concepts in the numerical convex lens (including the fractal model and the solving algorithm) based on a power electronics context. To establish the fractal model shown in Fig. 4 for MPE systems,we divide the system dynamics into two dynamic planes according to their timescales.The first-level dynamic plane describes the large-timescale system-level dynamics, where the switching-on and switching-off of the power switches are considered as discrete events.When the switch is in its steady state(onstate or off-state, modeled as small resistance or open-circuit,respectively),the system can be described with the state equation:

where x is the state vector,and each element of x is an independent state variable, namely the voltage of a capacitor and the current of an inductor; and u is the input vector, and each element of u is an input of the system, such as a power source. Moreover, it is shown in Eq.(13)that the state equation fswis dependent on sw,a switching function vector where each element is the switching state(on or off) of a switch.

For mode transition, namely, the switching event, the model must define the guard for each switching event,as Eq.(2)suggests.Here, we list the main guard conditions for switching events.

For a diode switch, the guard condition for its turn-on is when its voltage where vDis greater than zero:

The guard condition for an active switch(e.g.,an insulated gate bipolar transistor, or IGBT) is determined by the controller of the system.In power electronics,pulse-width modulation(PWM)control is usually used to determine the switching signals[41],where switching events are triggered when a reference waveform vref(which depends on system states) crosses a carrier waveform vcar(a regular signal). Thus, the guard condition of an active switch is

where vrefand vcarare the values of the reference and the carrier,respectively.

Thus far, the first-level dynamic plane in the fractal model has been established. To describe the transient of a discrete event in the first-level dynamic plane—namely, the switching transient of the semiconductor device—it is necessary to build a hybrid model of the second-level dynamic plane. Here, in order to model the switching behavior, we use the piecewise analytical transient(PAT)modeling method as described in Ref.[20].In the PAT model,the switching transient is divided into different stages according to the physical mechanisms inside the semiconductor device(Fig. 7).Each stage corresponds to one mode (one circle in Fig. 5) in the second-level dynamic plane.

Now that we have established the fractal model for MPE systems,with level-one and level-two dynamic planes,the next target is to solve the fractal model with the numerical convex lens. Following the principles of the numerical convex lens, our tasks include: ①to determine the numerical angular frequency for the continuous state variables; ②to determine the numerical light intensity for the discrete event variables; and ③to solve the system following the imaging principles. Below are descriptions of how these concepts are defined in MPE systems.

First, as defined above, the numerical angular frequency is the numerical measurement error and is dependent on the integration algorithm. For non-stiff circuits of MPE systems, we can use the flexible adaptive discrete state (FA-DS) integration algorithm to calculate the numerical solution of the continuous states [39].According to the algorithm, the numerical angular frequency is defined as follows:

Fig.7. PAT model of an IGBT-diode switching pair.The complicated physical mechanisms within semiconductors are decoupled,as shown in the left circuit.Only dominant mechanisms are considered in each stage of the switching transient,as shown in the right waveform.The relationship between the mechanisms and the stages are marked with colors. BJT refers to the bipolar junction transistor. Ls is the stray inductor and vLs is the voltage across it.CDC is the direct current-bus capacitor and VDC is the voltage across it.VGon,VGoff,RGon,and RGoff are the gate-drive voltages and resistances.RGint is the inner resistance of the gate node.Cgc,Cge,and Cce are the junction capacitances of the IGBT and vcg,vge,and vce are the voltages across them.DS is the diode,vD is the voltage across it,irr is the reverse recovery current of it,and iD is the current through it.Lload and Rload are the inductance and resistance of the load,and IL is the current through the load.ic is the current through the IGBT.ig is the gate-dive current of the IGBT.Icmax is the maximum current of the IGBT during the turn-on transient. t0 ～t6 are the time instants of each stage.

where x is one of the state variables (the inductor current of the capacitor voltage), xbaseis the base value of x, p is the order of the integration algorithm,xp+1denotes the(p+1)th-order derivatives of x,and Δt denotes how long the numerical integration lasts since the last calculation timepoint.

Based on the above definitions,ω(x,t)represents the estimated numerical error of the integration algorithm for state variable x at timepoint t,thus offering what the numerical convex lens requires for the imaging of continuous states: namely, the numerical measurement error(which denotes how much this state variable matters and whether we need to update the system states at this timepoint).

For the discrete events, the definition of the numerical light intensity of each discrete event has been given in Eq. (10). We define the base value for the discrete event solving cbaseas the maximum value of all the threshold values defined in the fractal model—that is, Eqs. (14–16)—and the absolute tolerance as a setting of the algorithm.

We can now solve the system following the image formation of the numerical convex lens, according to Eqs. (8–12) and Eq.(17). There are three parameters to control the simulation accuracy—that is, b, K, and β—which control the error tolerances of the continuous states, the discrete events, and the overall simulation, respectively. Once a clear imaging triggers a new calculation, we can use the discrete state algorithm to calculate the continuous states, or use the secant method [39] to locate the time of occurrence of discrete events. Furthermore, discrete events will be magnified into a second-level dynamic plane to simulate the switching transients.

4. Applications and validations in MPE systems

This section presents applications of the state-discretized approach in MPE systems. A 2 MW renewable energy system is taken as an example to test and verify the proposed modeling and simulation approach. The structure in Fig. 8 illustrates one of the operational modes of the system, with renewable energy and storage. The main component is a four-port electric energy router(EER)[34]that connects the utility grid,the renewables,the energy storage, and various types of loads.

The topology of the EER is shown in Fig. 9. In the studied system,one EER contains 576 switching devices;in theory,this means that the system has 2576possible operating modes in total. In addition, each mode transition is accompanied by a nanosecondlevel electromagnetic transient. This makes the system unsolvable with any time-discretized approaches and tools currently available, unless the mathematical model is greatly simplified, which would result in low accuracy.Even with simplifications from ignoring the switching transients of the discrete events, the simulation still takes much too long (up to hours or days). Consequently,due to huge challenges in numerical modeling and solving, the design and analysis of such a system have mainly relied on experience or simplification in the past.

To better elaborate the concept of the fractal model in the studied case,we show the mathematical form of the fractal model here,taking one high-voltage direct current (HVDC) submodule (Fig. 9)in the EER as an example.For the upper dynamic plane,if we define mode U1 as (SHD1= SHD4= 1, SHD2= SHD3= 0), and mode U2 as(SHD1= SHD4= 1, SHD2= SHD3= 0), we can derive the upper-level state equations within the fractal model as follows:

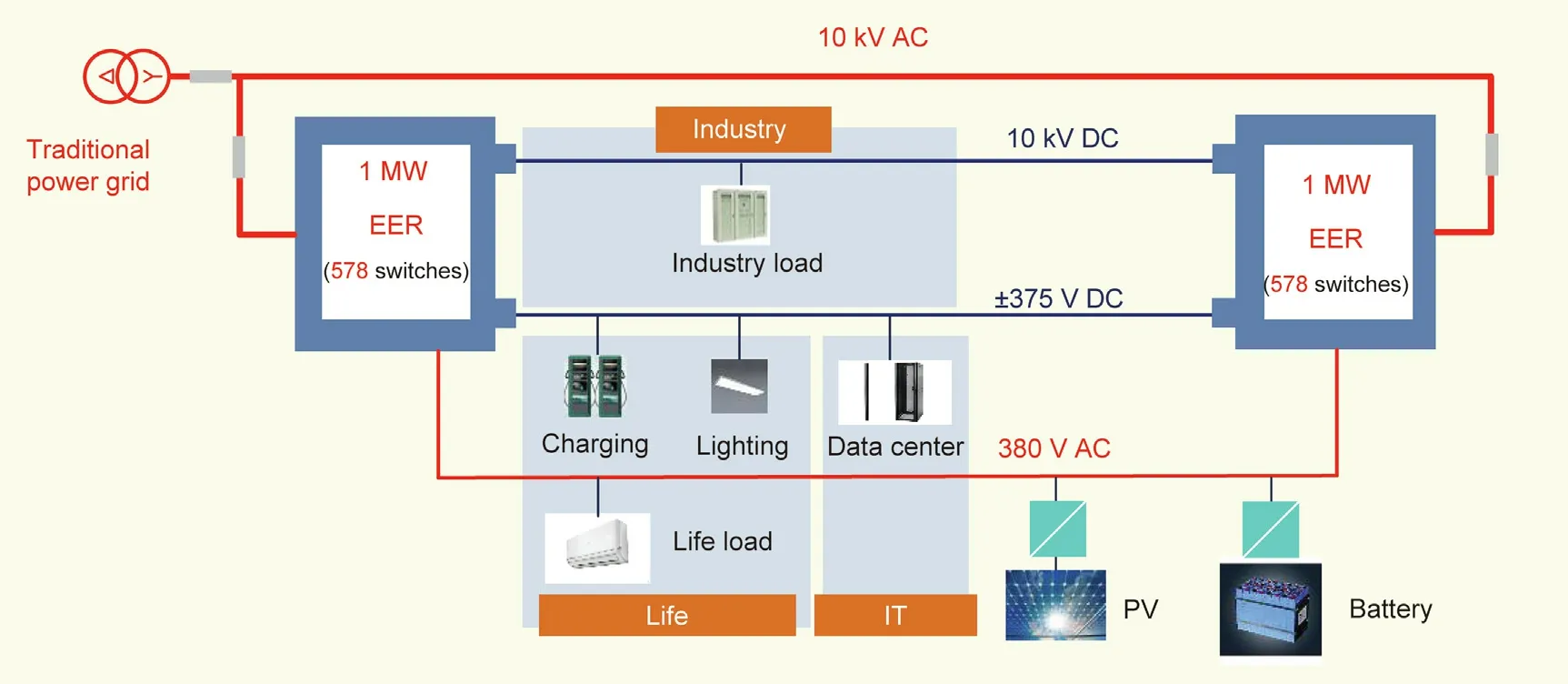
Fig. 8. Structure of the studied MPE system. IT refers to information technology, PV refers to photovoltaic, DC refers to direct current and AC refers to alternating current.EER: electric energy router.

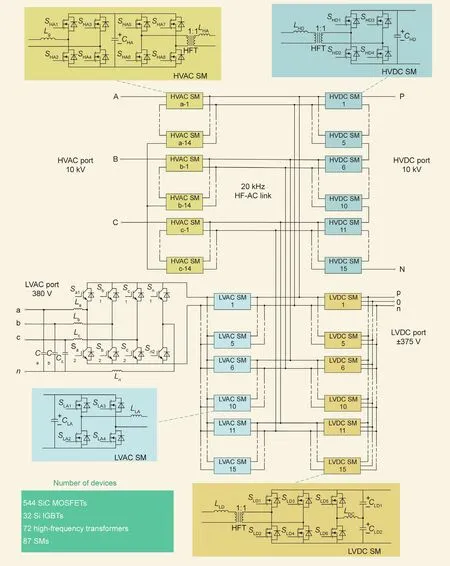
Fig. 9. Topology of one EER. It contains a 10 kV high-voltage alternating current (HVAC) port, a 10 kV high-voltage direct current (HVDC) port, a ±375 V low-voltage direct current(LVDC)port and a 380 V low-voltage alternating current(LVAC)port.A 20 kHz high-frequency alternating current(HF-AC)link is used as the AC bus inside the EER.One EER contains 87 submodules (SMs) and 72 high-frequency transformers (HFTs). SHD1, SHD2, SHD3, and SHD4 are the switching signals of the SiC MOSFETs in a HVDC SM.LHD and CHD are the inductance and capacitance in a HVDC SM.

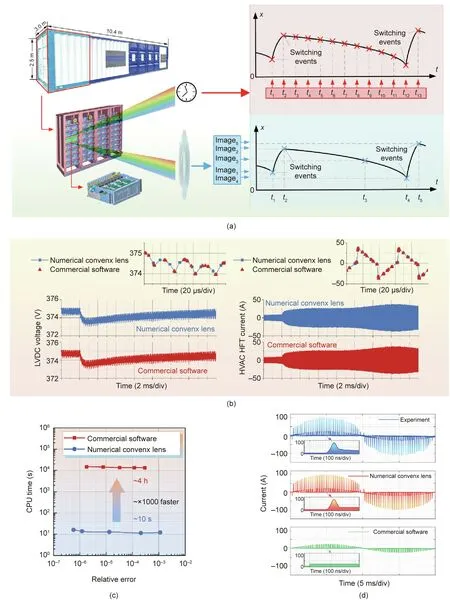
Fig. 10. Numerical experiments on the 2 MW system. (a) Diagram of the prototype and internal structure of the EER, and a comparison between the principles of timediscretization and state-discretization methods in a numerical experiment of power electronic hybrid systems.Comparisons of(b)simulated results and(c)simulated speed between the numerical convex lens and commercial simulation software based on time-discretization. (d) Comparison of switching-current simulated results between the numerical convex lens and commercial simulation software that uses an ideal switch model. ns/div: nanosecond per division; μs/div: microsecond per division;ms: millisecond per division.

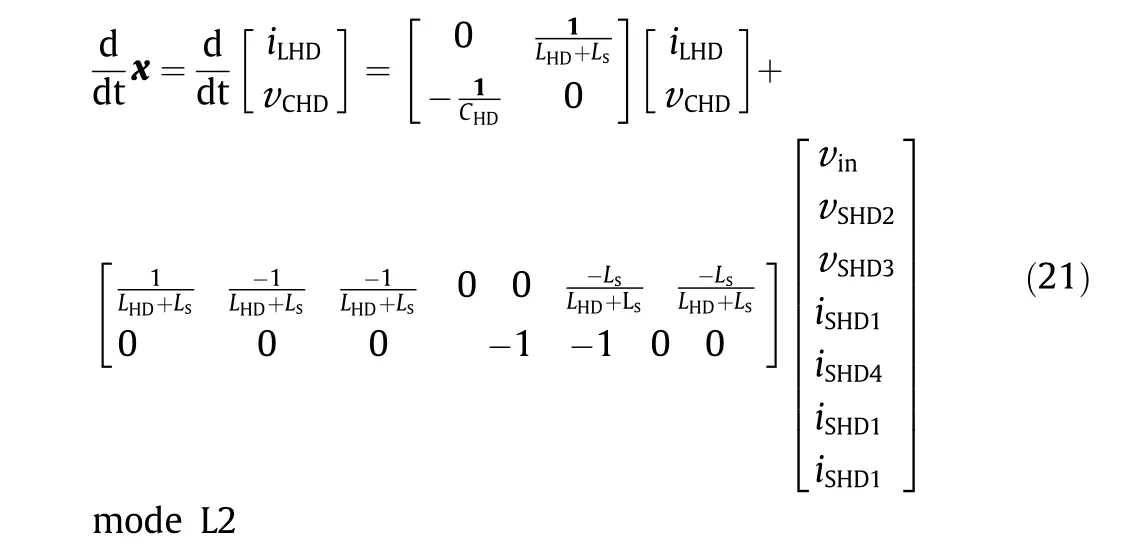
where Lsis the stray inductance as in Fig. 7, and vSHD2,vSHD3, iSHD1,and iSHD4are the equivalent voltage and current sources of the MOSFETs.

The expressions of vSHD2,vSHD3,vSHD1,and vSHD4are given by the PAT model[20].It can be found that the model for the upper-level dynamics—that is,Eqs.(18)and(19)—and the model for the lowerlevel transients—that is, Eqs. (20) and (21)—share very similar forms. This finding proves the concept of the fractal model; that is,when we zoom into the smaller timescale(Fig.4,the transients of the discrete events), the model shows similarity to the largertimescale model. These different timescales are all described by hybrid models,with multiple modes and states and algebraic equations in each mode.

Based on the fractal model above, a numerical platform can be built for this EER system.A 0.2 s load-change dynamic of one EER is tested.Compared with the time-discretization approach,the statediscretization approach enabled by the numerical convex lens can dramatically improve the calculation efficiency (Fig. 10(a)). A professional simulation software in the field of power electronics commercial is chosen as the benchmark.All the tests are performed on the same personal computer, with a 4.20 GHz Intel Core i7-7700K CPU and 32 GB of memory. When simulating a 200 ms dynamic process (where switching transients are ignored because no existing tools can solve the system otherwise), the numerical convex lens achieves more than 1000 times acceleration at the same accuracy,shortening the simulation time from nearly 4 h to around 10 s(Figs.10(b)and(c)).This result is achieved on an ordinary personal computer and does not involve any acceleration technology by multi-core computation in parallel. Furthermore, the numerical convex lens takes advantage of the fractal model to solve the switching transient of discrete events—that is, the nanosecondlevel electromagnetic transient—thus attaining high consistency with experimental results (the simulation time with the proposed approach is then 608 s for a 0.2 s simulation when considering the switching transients of all the semiconductor switches).To date,no other commercial simulation software has such capability; other software can only approximately regard the switching events as instantaneous (Fig. 10(d)). The accuracy and high speed of the numerical convex lens enables a groundbreaking revolution in the design and development of the MPE system:All designers will be able to verify its design efficiently and accurately, solve multitimescale dynamics,and perform virtual control tests at low hardware cost (i.e., an ordinary personal computer) and low time cost(seconds or minutes). With the numerical convex lens, designers can conduct the previously unimaginable and time-consuming simulation of system dynamics, and can even achieve automatic design and iteration by introducing artificial intelligent algorithms.

Another scenario of the EER is simulated to demonstrate the capability of the proposed numerical convex lens for addressing dynamic interactions across multiple timescales.In a real EER project, a high-frequency oscillation of 2 MHz is observed across the AC link[42].Due to the topology shown in Fig.10,this 2 MHz oscillation has a large influence on the stable operation of the system.It generates significant electromagnetic interference (EMI) and causes malfunctioning of the control system. Such highfrequency behavior is highly dependent on the small-timescale switching transients, while also having a large influence on the overall performance of the system. Therefore, this scenario provides typical evidence of the tight connection between multiple timescales in MPE systems [43]. With the numerical platform, we study the high-frequency oscillation with both a conventional gate driver(Fig.11(a))and an active gate driver(details of the design of the active driver can be found in Ref. [43]) (Fig. 11(b)). The simulated results show that with the active gate driver, which actively controls the voltage slew rate of the switching transient, it is largely possible to mitigate the high-frequency oscillations and therefore the corresponding EMI.

5. Conclusions

Although time-discretized simulation approaches have been well-developed for pure-continuous systems, the current bottleneck in the development of engineering systems lies in how to address emerging largescale complex systems, defined as GHSs,which involve both continuous states and discrete events across multiple time scales.To resolve this bottleneck,this paper demonstrated the numerical convex lens method to implement statediscretized modeling and simulation of GHSs. In the proposed approach,the calculated point is triggered by the imaging of a virtual convex lens, where the imaging process represents the discretization of the system states. Therefore, the discretized points can be naturally matched with the discrete events within GHSs.

The proposed approach can be universally used for all GHSs among various engineering fields. In this work, we applied and verified the proposed approach in MPE systems,which are increasingly being integrated in modern power grids during the transition toward a more sustainable energy system. A 1000-fold speedup was achieved using the proposed approach. Furthermore, this approach has the unique capability to simulate nanosecond-level switching transients in such largescale systems without convergence problems. This approach will advance the computing capability and extend the limitations of numerical prototypes in engineering systems, such that simulations of complicated GHSs are no longer a bottleneck.

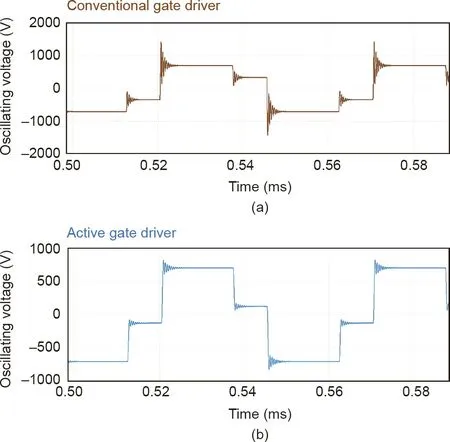
Fig.11. Simulated results of high-frequency oscillation with(a)a conventional gate driver and (b) an active gate driver.

Acknowledgments

This work was supported by the Major Program of National Natural Science Foundation of China (51490683).

Compliance with ethics guidelines

Bochen Shi,Zhengming Zhao,Yicheng Zhu,Zhujun Yu,and Jiahe Ju declare that they have no conflict of interest or financial conflicts to disclose.