High-frequency characterization of high-speed modulators and photodetectors in a link with low-speed photonic sampling

Mengke Wang, Shangjian Zhang, Zhao Liu, Xuyan Zhang, Yutong He, Yangxue Ma, Yali Zhang,Zhiyao Zhang, and Yong Liu

State Key Laboratory of Electronic Thin Films and Integrated Devices, School of Optoelectronic Science and Engineering, University of Electronic Science and Technology of China, Chengdu 610054, China

Abstract: We propose a low-speed photonic sampling for independent high-frequency characterization of a Mach-Zehnder modulator (MZM) and a photodetector (PD) in an optical link. A low-speed mode-locked laser diode (MLLD) provides an ultrawideband optical stimulus with scalable frequency range, working as the photonic sampling source of the link. The uneven spectrum lines of the MLLD are firstly characterized with symmetric modulation within the interesting frequency range. Then, the electro-optic modulated signals are down-converted to the first Nyquist frequency range, yielding the self-referenced extraction of modulation depth and half-wave voltage of the MZM without correcting the responsivity fluctuation of the PD in the link. Finally, the frequency responsivity of the PD is self-referenced measured under null modulation of the MZM. As frequency responses of the MZM and the PD can be independently obtained, our method allows self-referenced high-frequency measurement for a high-speed optical link. In the proof-of-concept experiment, a 96.9 MS/s MLLD is used for measuring a MZM and a PD within the frequency range up to 50 GHz. The consistency between our method and the conventional method verifies that the ultra-wideband and self-referenced high-frequency characterization of high-speed MZMs and PDs.

Key words: frequency response; modulators; photodetectors; low-speed photonic sampling; microwave photonics

1.Introduction

High-speed optoelectronic devices including an electrooptic Mach-Zehnder modulator (MZM) and photodetector(PD) are basic but are key components in radio-over-fiber communication systems, optical communication systems and microwave photonic signal processers[1-3], which perform as precise optical-to-electrical (O/E) or electrical-to-optical (E/O)signal converter[4,5]. Their frequency responses have a great impact on device characterization and system optimization, especially for ultra-wideband applications, leading to a challenge for device measurement over a wideband frequency range.

In most cases, modulators (MODs) and PDs are separately measured with different schemes and methods. There are a variety of optical or electrical methods proposed to characterize MZMs, including the optical spectrum analysis method, the electrical spectrum frequency-swept method and the electro-optic heterodyne mixing method, or to characterize PDs, including the optical noise-beating method, the optical pulse excitation method, the optical wavelength-beating method, the electrical spectrum frequency-swept method, and the electro-optic heterodyne mixing method. The optical spectrum analysis method enables the calibration-free measurement of the MZM, benefiting from the optical spectrum analysis in the optical domain[6-8]. However, the grating-based optical spectrum analyzers (OSAs) have a limited resolution of 0.01 nm (about 1.25 GHz at 1550 nm). The resolution could be improved up to tens of MHz with the help of a heterodyne or Brillion OSA, nevertheless the measurement is often affected by the wavelength line-width and accuracy of the laser source. The optical noise-beating method utilizes the amplified spontaneous emission (ASE) noise to generate an ultra-wideband optical stimulus for the PD under test[9-12],however the measurement suffers from poor signal-to-noise ratio and small dynamic range. The optical pulse excitation method needs complex calibrations for the response of the oscilloscope and the amplitude fluctuation of the optical pulse source[13,14]. The optical wavelength-beating method requires an extra tunable laser as the local oscillator (LO)[15-19]for the PD and depends on a tunable laser with ultra-narrow linewidth and extremely stable power.

For high resolution, the electrical spectrum frequencyswept method was migrated from microwave measurement to optoelectronic measurement with the help of a microwave network analyzer[20-22], and is widely used for characterizing both E/O devices and O/E devices provided that there are standard O/E or E/O transducers for extra E/O or O/E calibration. In order to simplify the calibration, the improved frequency-swept method was proposed for measuring MODs and PDs with the help of an electro-absorption modulator (EAM) used as a MOD and a PD, provided that the EAM can be used for E/O modulation and O/E detection with the same frequency response[21,23]. Recently, we proposed electro-optic heterodyne mixing methods for self-calibrated frequency response measurements of both MZMs or PDs based on heterodyne spectrum mapping[24], or electro-optic modulation mixing[25,26], which eliminate the extra O/E or E/O calibration by using frequency-shifted heterodyne and/or two-tone modulation[27]. In order to extend the measuring frequency range, we employed a low-speed mode-locked laser diode (MLLD) working as the ultra-wideband LO and presented a photonic down-conversion sampling for ultrawideband frequency response measurement of MZMs[28].However, the method in Ref. [28] assumes that the MLLD features very wide spectra lines with extreme flatness. Therefore,electro-optic methods that can achieve high-frequency response measurements of MZMs and PDs with ultra-wide frequency range and self-referenced capability are of particular attraction.

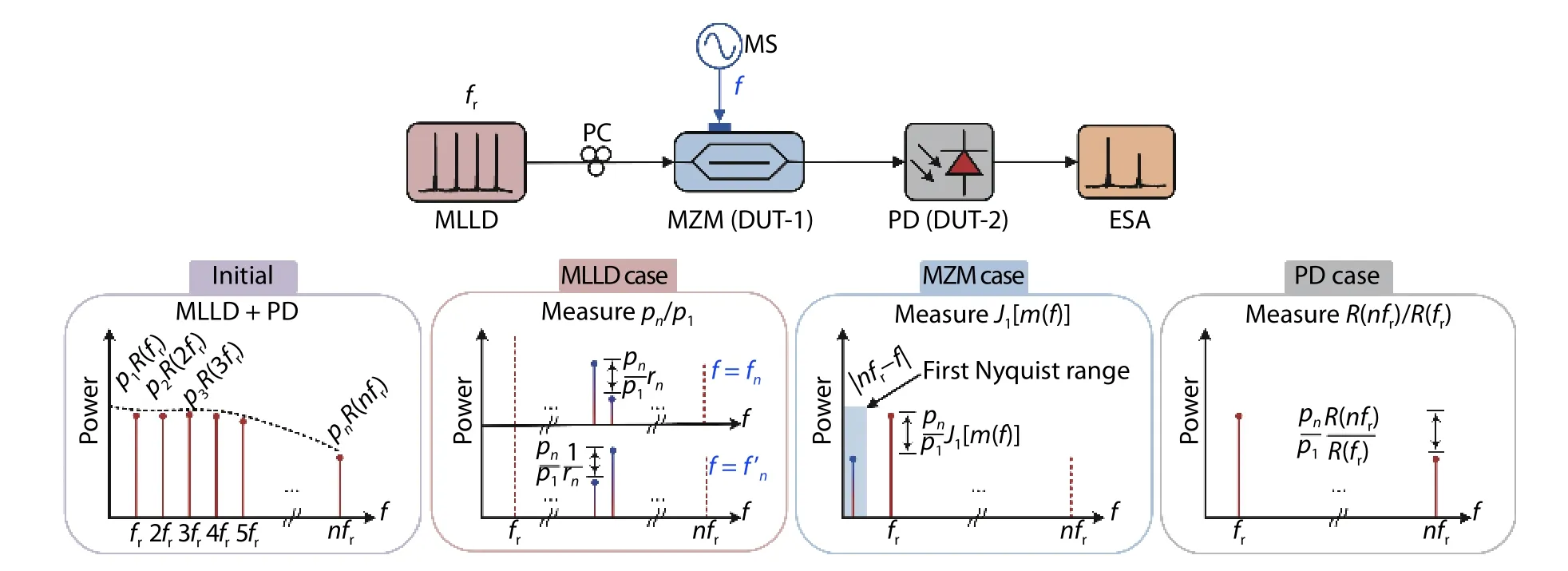
Fig. 1. (Color online) Schematic diagram of the proposed method based on low-speed photonic sampling. MLLD: passively mode-locked laser diode, PC: polarization controller. MZM: electro-optic Mach-Zehnder modulator. DUT: device under test. MS: microwave source. PD: photodetector. ESA: electrical spectrum analyzer.

In this work, we propose a low-speed photonic sampling for independent high-frequency characterization of highspeed MZMs and PDs in an optical link. As is shown in Fig. 1,the method consists of an MLLD, an MZM under test and a PD under test. The low-repetition-frequency MLLD provides an ultra-wideband optical stimulus with scalable frequency range, working as the photonic sampling source of the MZM and the PD in the link. Different from Ref. [28], the uneven spectra lines of the MLLD are firstly characterized with symmetric modulation within the interesting frequency range. Then,the electro-optic modulated signals are down-converted to the first Nyquist frequency range, yielding the self-referenced extraction of modulation depth and half-wave voltage of the MZM without correcting the responsivity fluctuation of the PD in the link. Finally, the frequency responsivity of the PD is self-referenced measured under null modulation of the MZM. The method avoids any extra calibration for the frequency response of PD in the case of the MZM under test or the frequency response of the MZM in the case of the PD under test, because they can be totally canceled out by the symmetric frequency components. Therefore, frequency responses of MZMs and PDs can be independently obtained,and our method allows self-referenced high-frequency measurement for high-speed optical link. Theoretical description and experimental demonstration are presented to fully confirm our scheme. All the results are compared to those obtained with the conventional method for the consistency and accuracy.

2.Operation principle

As shown in Fig. 1, a low-repetition-frequency optical comb from the MLLD is used as an optical source to send into the MZM under test, and modulated by the electrical signal from the microwave source (MS). The output photonic sampling signals are detected by the PD under test and analyzed by an electrical spectrum analyzer (ESA). The optical comb from MLLD can be written as[28]



with the amplitude Vωof the electrical signal and the halfwave voltage Vπ(ω) of the MZM at the frequency ω. Then the photonic sampling signals are sent into the PD under test,and the generated instantaneous photocurrent can be expanded with the help of the Jacobi-Anger theorem[29], given by



where R is the responsivity of the PD, Jk(m) is the k-order Bessel function of the first kind, p0and pnrepresent the DC and AC intensity of the comb lines from the MLLD, respectively, expressed by



which are related to the intensity pnof comb lines from the MLLD, the modulation depth m of the MZM and the responsivity R of the PD, respectively.

For characterizing the uneven spectra lines of the MLLD,the MS is firstly set at the symmetric frequencies of ωn= [(n -1)/2]ωr- Δω and ω’n= [(n - 1)/2]ωr+ Δω [n = 1-(N1+ N2)], respectively. According to Eq. (5(b)), we have



Because of ωn+ ω’n= (n - 1)ωr, the PD responsivities of R(ωr+ ωn) = R(nωr- ω’n) and R(nωr- ωn) = R(ωr+ ω’n) will hold,and we set rn= R(nωr- ωn)/R(ωr+ ωn) = R(ωr+ ω’n)/R(nωr- ω’n).Therefore, the uneven response pn/p1induced by the comb lines from the MLLD can be expressed as



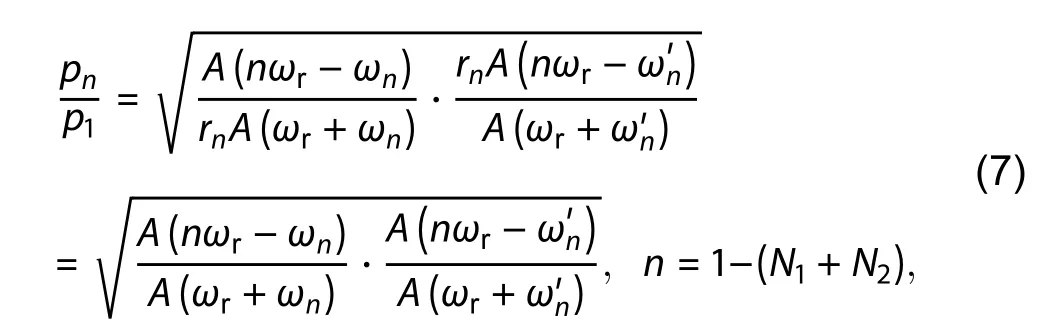
which is independent of the bias phase of the MZM since the bias phase has the same influence on these frequency components and can be totally cancelled out through the relative amplitude.

Then, in the case of the MZM under test (DUT-1), the electrical signal at any frequency of ω is applied onto the MZM and down-converted to the first Nyquist frequency range of 0-ωr/2, obtaining the desired frequency components at|nωr-ω| and ωr, which can be written by, based on Eqs. (5a)and (5b)



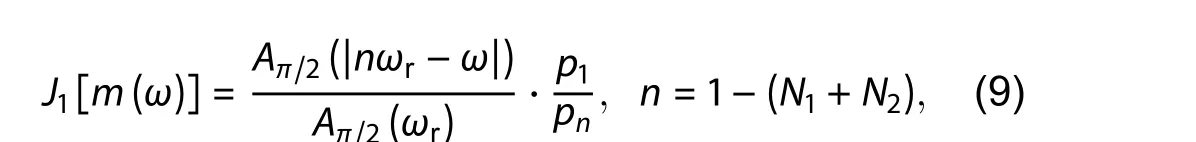
where n = round(ω/ωr), indicating that ω/ωris round to the nearest integer. Since the repetition frequency ωrof a passively MLLD is about tens of megahertz or below in practice,we assume that R(ωr) ≈ R(|nωr-ω|). Therefore, the modulation depth m(ω) can be written as with the uneven response pn/p1of the MLLD from Eq. (7).The half-wave voltage Vπ(ω) of the MZM at the modulation frequency ω can be extracted with the help of Eq. (3). It should be noted that the responsivity of the PD is canceled out by the relative amplitude of these two frequency components and any extra O/E calibration is not required.

In the case of the PD under test (DUT-2), the MZM works under null modulation, that is, there is no microwave signal applied on the MZM, and the frequency components at the repetition frequency nωrcan be obtained based on Eq. (5a). Therefore, the frequency response of PD at the frequency nωrwith respect to the fixed low-frequency ωrcan be expressed by



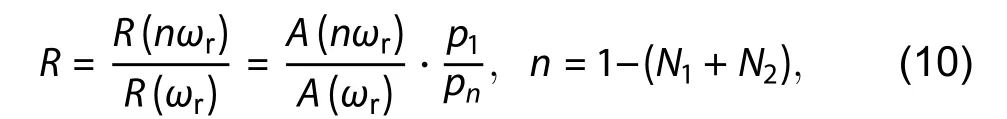
which relates to the uneven response pn/p1of the MLLD from Eq. (7).

Finally, the ultra-wideband frequency responses of both MZM and PD can be self-referenced measured based on the low-speed photonic sampling. It is worth noticing that the frequency responses of the MZM and PD are independently extracted, which eliminates any extra calibration for the frequency response of the PD in the case of the MZM under test or the frequency of the MZM in the case of the PD under test,since they are canceled out by the carefully chosen frequency components.

3.Experimental demonstration

In the experiment, a 96.9 Ms/s MLLD is used as the optical source to sample the electrical signal via the MZM under test (EOSPACE), and the output photonic sampling signals are collected by the PD under test (DSC) and analyzed by an ESA (R&S FSU50).

To extract the uneven response of the MLLD within the frequency range of 50 GHz, the symmetric frequencies of the MS are set as fn= [(n - 1)/2]fr- Δf and f’n= [(n - 1)/2]fr+ Δf(n = 1-516, fr= 96.9 MHz, Δf = 2 MHz), respectively. The desired four frequency components can be obtained, including fr+ fn, nfr- fn, nfr- f’nand fr+ f’n, as illustrated in Fig. 2. For example, when the frequency of the MS is set to be f516=[(516 - 1)/2] × 96.9 - 2 MHz, the desired two frequency components at 25.04665 GHz (fr+ f516) and 25.05065 GHz(516fr- f516) are measured to be -67.43 and -77.51 dBm.Then, when the symmetric frequency of the MS is set to be f’516= [(516 - 1)/2] × 96.9 + 2 MHz, the desired two frequency components at 25.04665 GHz (516fr- f’516) and 25.05065 GHz (fr+ f’516) are measured to be -77.76 dBm and-69.76 dBm. Therefore, the uneven response p516/p1induced by the comb lines from the MLLD can be calculated as-9.04 dB according to Eq. (7). Similarly, when the symmetric frequencies of the MS are sweeping from f516to f1and f’516to f’1(n = 516, 515, …, 1), the uneven response pn/p1induced by the comb lines from the MLLD can be determined within the interesting frequency range of 50 GHz, as shown in Fig. 3.

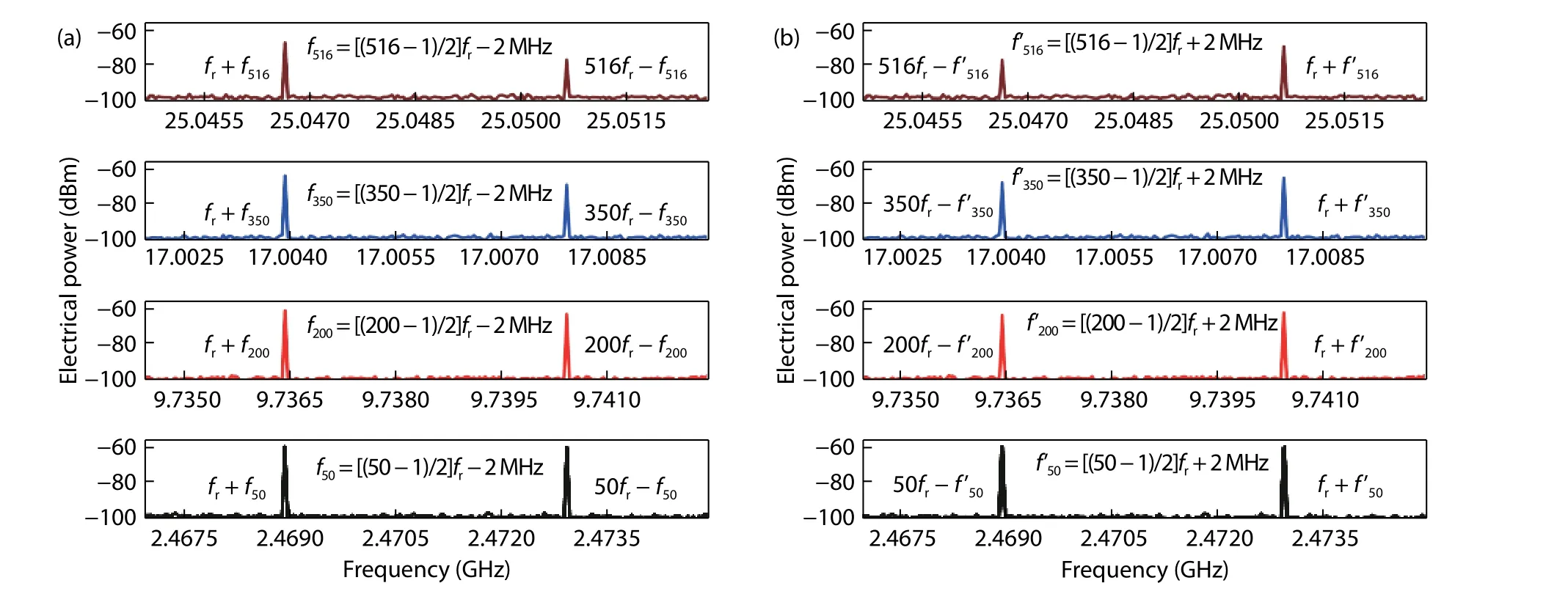
Fig. 2. (Color online) Measured electrical spectra of photonic sampling signals at different symmetric modulation frequencies for extracting the uneven response of the MLLD.

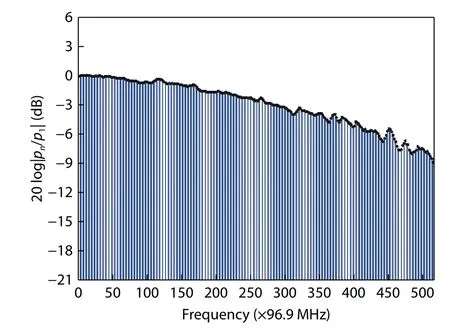
Fig. 3. (Color online) Measured uneven response pn/p1 induced by the comb lines from the MLLD.

Fig. 4. (Color online) Measured typical electrical spectra of the MZM under test at different modulation frequencies.

Fig. 5. Measured modulation depth and microwave driving power applied on the MZM.

In the MZM measurement (DUT-1), the electrical signal at any frequency of f is loaded onto the MZM to acquire the desired two frequency components at |nfr- f| and frafter the PD, and the bias phase ψ = π/2 are achieved by changing the applied bias voltage of MZM, which corresponds to the maximum amplitude of the frequency components at |nfr- f|. Fig. 4 shows the measured typical electrical spectra of the MZM under test at different modulation frequencies. For example,when the frequency of MS is set as f = 49.96 GHz, the obtained two low-frequency components at 40.4 MHz (=516fr- f) and 96.9 MHz (fr) are measured to be -77.45 and-41.75 dBm. Meanwhile, the uneven response p516/p1induced by the comb lines from the MLLD has been calculated as -9.04 dB. Therefore, the modulation depth m of the MZM at the modulation frequency 49.96 GHz is solved to be 0.093 based on the Eq. (9). In addition, the actual microwave amplitude of the electrical signal applied on the MZM is measured to be 0.316 V (-0.01 dBm), thus the half-wave voltage is determined to be 10.670 V at 49.96 GHz according to Eq. (3).

The measurement can be easily operated at other frequencies by simply setting the frequency of the MS. Fig. 5 shows the measured frequency-dependent modulation depth and the microwave driving powers applied on the MZM for reference, from which the half-wave voltage can be calculated as a function of modulation frequency, as illustrated in Fig. 6.The half-wave voltage measured with the electro-optic heterodyne mixing method is also shown in Fig. 6 for comparison.Meanwhile, the relative frequency response of the MZM can be calculated based on the half-wave voltage, as shown in Fig. 6, where their good consistency between two methods verifies that our method can self-reference extract the absolute frequency response of the MZM.

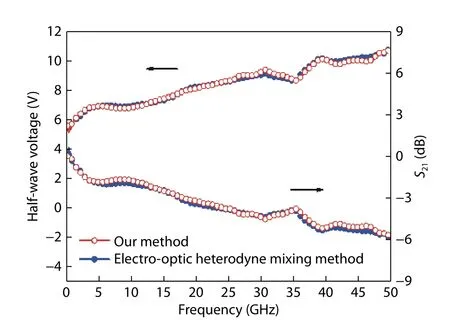
Fig. 6. (Color online) Measured half-wave voltage and relative frequency response of the MZM under test with our method (red open circles) and the electro-optic heterodyne mixing method (blue solid circles).

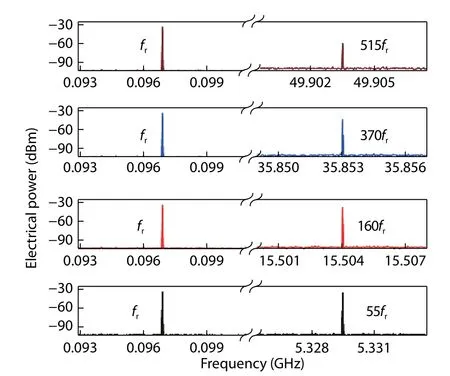
Fig. 7. Measured electrical spectra of the repetition frequencies nfr when the MZM works with null modulation, in the case of the PD under test.

In the PD measurement (DUT-2), there is no electrical signal output from the MS, and the MZM works under null modulation. The frequency component at the repetition frequencies nfrcan be obtained, as presented in Fig. 7. For example,in the case of n = 515, the desired two frequency components are measured to be -33.95 dBm at 96.9 MHz (fr) and-58.96 dBm at 49.9035 GHz (515fr), respectively, and the uneven response p515/p1induced by the comb lines from the MLLD has been calculated as -8.85 dB. Therefore, the responsivity of PD at the frequency 49.9035 GHz (515fr) with respect to the fixed low-frequency 96.9 MHz (fr) is determined to be-16.16 dB based on Eq. (10). Similarly, the relative responsivity of PD at other repetition frequency nfrcan be extracted by simply changing the value of n, as displayed in Fig. 8. The experimental results obtained with the electro-optic heterodyne mixing method is also shown in Fig. 8 for comparison,and the consistency demonstrates that our method enables the self-referenced frequency response of PD within the ultra-wide frequency range based on low-speed photonic sampling.

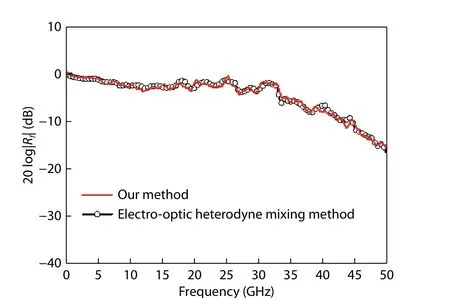
Fig. 8. (Color online) Measured frequency response of PD under test with our method (red line) and the electro-optic heterodyne mixing method (open circles).

4.Measurement uncertainty

For measurement accuracy, we firstly study the measurement uncertainty of the uneven response pn/p1induced by the comb lines from the MLLD, which can be obtained by the total derivative of Eq. (7), given by



According to the specification of the ESA, the measured electrical power has a maximum uncertainty of 0.1 dB or the amplitude has an uncertainty of less than 0.05 dB. Thus, the measurement uncertainty of the uneven response pn/p1of MLLD will be less than 0.1 dB (= 0.05 × 4 × 0.5), corresponding to a relative error of less than 1.16% [= (100.1/20-1) × 100%].

Then, in the case of the MZM under test (DUT-1), we investigate the error dependence of modulation depth m on the uncertainty of J1(m) by the error transfer factor, written as



which is deduced from the total derivative of Eq. (9). As is shown in Fig. 9, the error transfer factor F is less than 1.1 in the case of the modulation depth m ＜ 0.4. In our experiment,the main error sources of J1(m) come from the uncertainty of ESA, the uncertainty of the uneven response pn/p1induced by the comb lines of the MLLD and the response fluctuation of the PD because our method is based on the approximation of R(ωr) ≈ R(|nωr- ω|) from Eq. (9). In the experiment, we can see that the 3-dB bandwidth of the PD is measured to be 33 GHz, so the responsivity difference of the PD within 96.9 MHz frequency difference is estimated to be less than 0.2 dB. Therefore, J1(m) would have an uncertainty of less than 0.4 dB (= 0.05 × 2 + 0.1 + 0.2), which means a relative error of less than 5.18% [= 1.1 × (100.4/20- 1) × 100%] delivered to the extracted modulation depth m. Similarly, the uncertainty of the half-wave voltage can be written by the total derivative of Eq. (3), given by



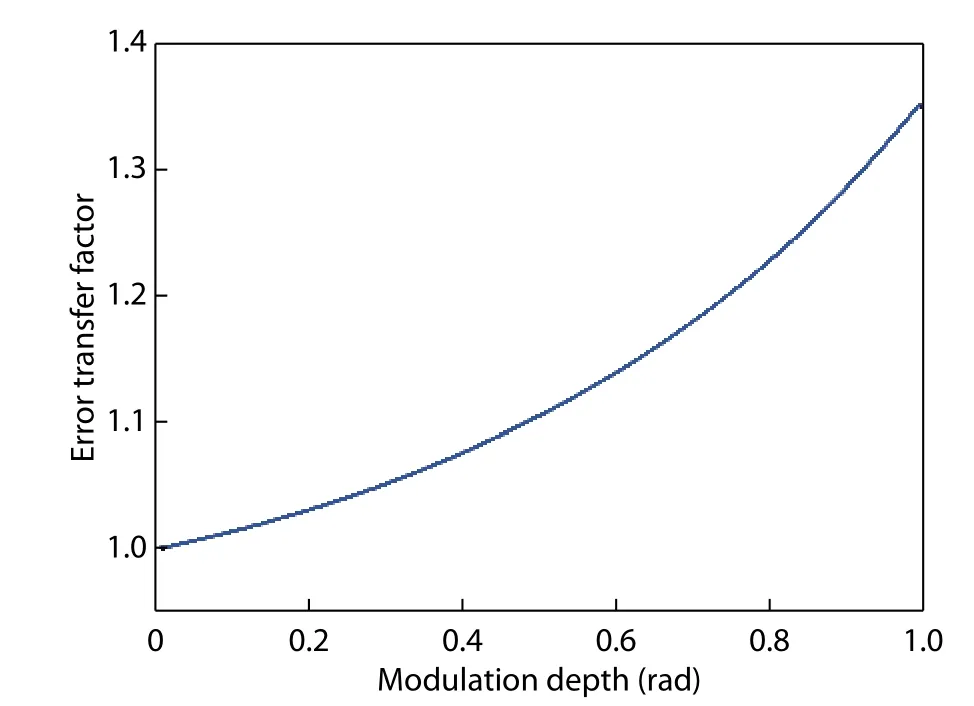
Fig. 9. Error transfer factor as a function of modulation depth.

Therefore, the total relative error of less than 5.76% [=5.18% + (100.05/20-1) × 100%] is transferred to the measured half-wave voltage in the worst case.

Finally, in the case of the PD under test (DUT-2), the measurement uncertainty of the frequency response can be derived from the total derivative of Eq. (10), expressed by



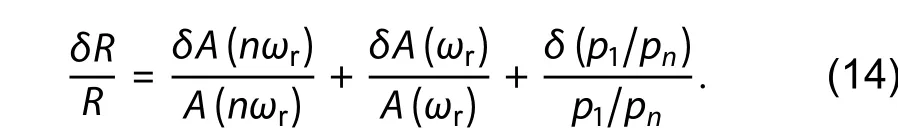
Thus, the PD responsivity at the repetition frequency nωrwith respect to the fixed low-frequency ωris measured with a relative error of no more than 2.33% (= [10(0.05×2+0.1)/20-1] × 100%) in the worst case.

We also make the accuracy comparison between our method and the electro-optic heterodyne mixing method in Ref. [24]. In our method, the relative errors of less than 5.76%and 2.33% might be transferred to the measured results of the MZM and PD in the worst case, respectively. However, in the method of Ref. [24], the measured results of the MZM and PD might have the relative errors of less than 8.87% and 2.30%, respectively.

5.Conclusion

Compared with the optical methods, the proposed method enables high-frequency measurement of MZMs and PDs with high resolution, in which the photonic sampling signals show extremely narrow spectrum lines due to the inherent coherence of the optical frequency comb originating from the same MLLD. Different from the electrical spectrum frequencyswept method, it achieves the self-referenced frequency response measurement of the MZM and the PD through the low-speed photonic sampling without any complex O/E or E/O calibration. In contrast to the electro-optic heterodyne mixing methods, our method realizes high-frequency characterization of MZM and PD with self-reference capability in ultra-wideband measuring frequency range. Prior to our work in Ref. [28], this scheme can be operated even under the case of an MLLD without flat spectra lines, which largely alleviates the requirement for the MLLD source.

In summary, we have demonstrated a self-referenced and ultra-wideband high-frequency characterization of a high-speed MZM and PD in an optical link based on lowspeed photonic sampling. The method enables the independent frequency response measurements of MZM and PD in a shared link, and eliminates any extra calibration for the frequency response of the PD in the case of the MZM under test or the frequency response of the MZM in the case of the PD under test by the carefully chosen frequency components.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (2019YFB2203500), the National Natural Science Foundation of China (NSFC)(61927821), the Joint Research Fund of Ministry of Education of China (6141A02022436), and the Fundamental Research Funds for the Central Universities (ZYGX2019Z011).