带分布时滞分数阶微分方程非振动解的存在性
2021-04-21 03:38:22刘有军赵环环
山西大学学报(自然科学版) 2021年1期
刘有军,赵环环
(山西大同大学,数学与统计学院,山西 大同 037009)
0 引言
由于分数阶微分方程越来越多地体现在力学和材料系统、热学和光学系统、流变学、信号处理、系统识别等应用型问题的描述中,这也就吸引了众多的国内外学者对其的理论研究做了一定的工作[1-3]。与此同时,泛函微分方程的振动理论由于其有重要的理论价值和现实意义,也得到了蓬勃的发展[4-8],其中一个重要分支——非振动解的存在性,发展较好[9-19]。
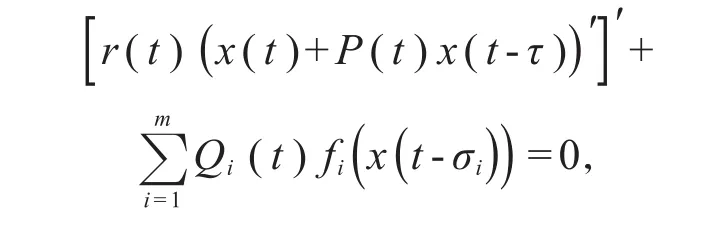
在2007年,周等[19]讨论了二阶多时滞微分方程得到了其非振动解存在的充分条件。但这些论文主要集中在整数阶的研究,2017年,周等[20]研究了常系数分数阶微分方程
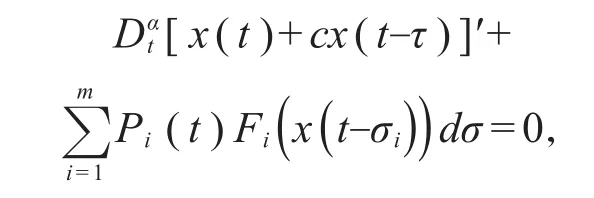
也得到了类似的结果。通过对上面文章的认真分析,在2019年,赵等[21]研究了多时滞变系数分数阶微分方程
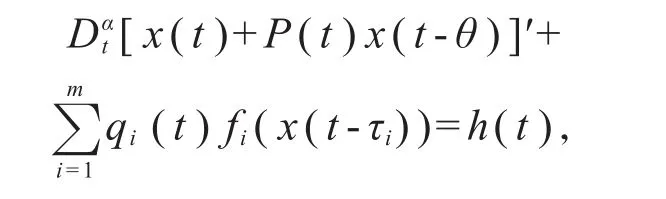
此文研究了离散时滞的情形,但由于连续时滞分别反映的不同学科的应用问题,而且此类结果还不多

1 主要结果




猜你喜欢
辽宁丝绸(2022年1期)2022-03-29 00:59:06
Chinese Physics B(2021年7期)2021-07-30 07:42:54
数学物理学报(2020年5期)2020-11-26 06:06:48
四川工商学院学术新视野(2020年1期)2020-07-24 09:04:54
西南石油大学学报(自然科学版)(2019年5期)2019-12-20 07:01:02
中学生数理化·中考版(2017年6期)2017-11-09 02:46:51
电气化铁道(2017年1期)2017-04-16 06:00:15
现代企业(2015年5期)2015-02-28 18:50:43
四川师范大学学报(自然科学版)(2015年2期)2015-02-28 14:07:40
应用数学与计算数学学报(2014年3期)2014-09-26 12:03:52

