基于最大转矩电流比的永磁同步电机自适应滑模控制

葛晨阳　孙新程　闫天一　胡继磊

摘要：针对永磁同步电机伺服系统在外部扰动力矩下的速度跟踪控制问题，提出了一种基于最大转矩电流比的自适应滑模控制器。为了简化计算，采用牛顿-拉夫逊迭代法实现最大转矩电流比对电机交直轴电流的分配，并在此基础上改进了自适应滑模速度控制器。为减少滑模控制中的抖振，设计了自适应滑模切换增益。通过仿真实验对比可知，所提控制方式有效提升了系统的动态响应能力、稳态性能和抗扰动能力。

关键词：内置式永磁同步电机;最大转矩电流比;自适应滑模控制;抗扰动能力

0 引言

内置式永磁同步电机（Interior Permanent Magnet Synchronous Motor，IPMSM）因其体积小、结构简单、功率密度高等优点，近年来被大量应用于飞轮储能、电动汽车、轨道交通等需要输出转矩大、动态响应快、调速范围宽的场合。目前，传统的永磁同步电机大量采用的是id=0的矢量控制方式，该控制方式易于实现，非常适合于表面式永磁同步电机（Surface Permanent Magnet Synchronous Motor，SPMSM）。但是由于IPMSM转子结构的特殊性，采用id=0的控制方法会提高电机铜耗，降低电流利用效率，间接提高了系统容量。

最大转矩电流比（Maximum Torque Per Ampere，MTPA）的控制方法可以充分利用IPMSM转子磁路的不对称性所产生的磁阻转矩，提高电机功率密度。但是其电磁转矩Te与交直轴电流id、iq之间存在着非线性的耦合项，增加了计算难度。文献[1]通过传统的查表法计算不同电磁转矩Te对应的id、iq的值，但是这种方法需要大量的数据存储空间;文献[2]提出了基于IPMSM的非线性磁链模型对d轴磁链和电流、q轴磁链和电流分别拟合，得到相应的转矩方程和MTPA条件，但是这种方法对实际系统的运算能力要求较高。

滑动模态控制（Sliding Mode Control，SMC）具有快速响应、对参数和扰动变化不敏感、参数设计无须系统在线辨识等优点，被大量应用于非线性系统的控制中。文献[3]设计了离散的滑模电流控制器，但是忽略了切换项中的不连续性的影响;文献[4]通过引入“准滑动模态”和“边界层”，采用饱和函数来设计切换函数，减弱了抖振，但是饱和函数的设计还是存在不连续性，参数无法实现自适应变化;文献[5]采用模糊控制方法在线调整切换系数，但是滑模控制器中切换系数过多，模糊规则的设计需要大量的工程经验。

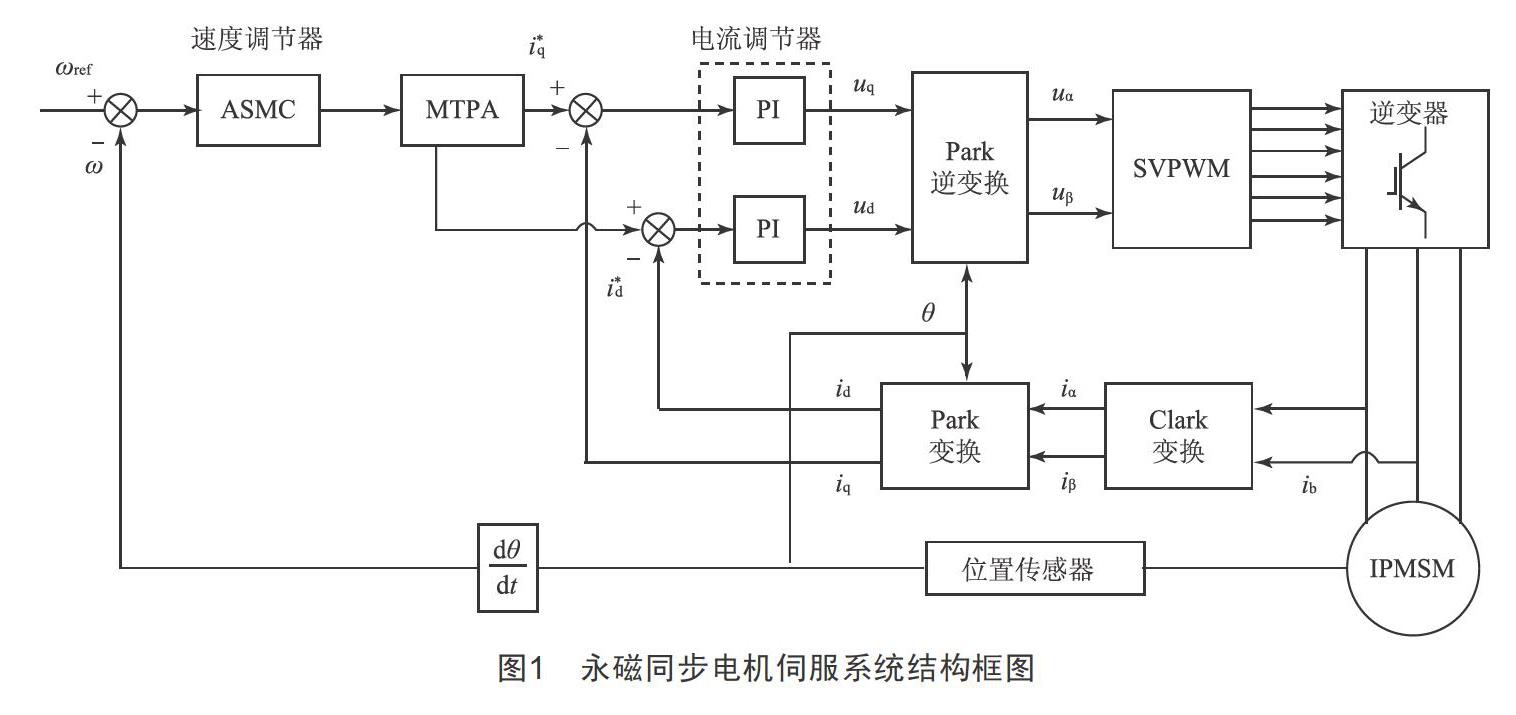
本文以存在外部扰动力矩的永磁同步电机伺服系统为研究对象，结合MTPA与滑模控制方法的优点，提出了一种基于MTPA的自适应滑模控制（Adaptive Sliding Mode Control，ASMC）方法，系统结构框图如图1所示。MTPA控制采用牛顿-拉夫逊迭代计算方法，降低了计算复杂性，提高了工程实用价值。滑模速度控制器中改进了滑模控制律的设计，将自适应控制引入传统的滑模切换项中，使滑模切换增益根据系统到达滑模面的距离自适应调节，降低系统抖振，提高系统动态和稳态性能。对比仿真结果表明，本文设计的控制方法明显提升了电机的速度和转矩响应，系统鲁棒性更好。

1 外部扰动下的永磁同步电机数学模型

永磁同步电机在d-q坐标系下的数学模型可用如下的定子电压方程、电磁转矩方程以及机械运动方程表示：

式中：id、iq、ud、uq、Ld、Lq分别为定子电流、电压和电感在d-q轴上的分量;R为定子的电阻;ψf为永磁体磁链;pn为电机的极对数;J为转动惯量;F为阻尼系数;Te为电磁转矩;TL为负载转矩;Δ为系统受到的扰动力矩;ωm为电机的机械角速度;θm为转子位置角。

结合实际系统中负载力矩、系统参数的变化在一定范围内都是有界的，可以作出如下假设：

假设1：系统的扰动力矩及其变化有界，即存在常数d0>0和d1>0，使得|Δ|≤d0，||≤d1。

假设2：系统的负载力矩在不改变电机负载的情况下为恒定值，其变化量全部等效为扰动力矩。

假设3：由假设1和假设2可得，电机输出的电磁转矩一阶导数连续且有界。

假设4：伺服系统工作在力矩和调速模式，给定的运动轨迹参考值ωref一阶导数连续且有界，二阶导数有界。

通过公式（1）和上述假设可以推出：

2 基于牛顿-拉夫逊迭代法的MTPA实现

最大转矩电流比可以理解为在输出相同的电磁转矩下，需要提供的定子电流值最小，即如式（3）表示的一个极值问题：

4 仿真研究与分析

为验证本文所提控制方法的有效性，在MATLAB/Simulink环境下搭建了仿真模型。其中，采用MTPA的矢量控制方式，基于本文提出的自适应滑模控制原理设计了滑模速度控制器，电流控制器采用了PI控制器。其系统结构框图如图1所示。仿真所选的永磁同步电机参数如表1所示。

自适应滑模控制器的参数设置为：c1=25，c2=10，q=150，ε=2，η0=100，λ=0.004，σ=100，μ=20。系统的外部干扰Δ=

0.5sin（50πt）N/m。图4、图5分别是本文所提控制方式与基于id=0的滑模速度控制器的对比结果。当电机处于调速模式下时，负载转矩恒定为5 Nm，在t=0 s时，给定转速为500 r/min。在t=0.25 s时，转速突变为1 500 r/min。由图4（a）可以看出，基于MTPA的ASMC转速响应更快、转速受扰动影响更小，稳态误差更小。由图4（b）可以看出，当电机启动时，MTPA控制方法能够提高电磁转矩的响应，而ASMC控制方法能够快速降低电磁转矩的超调，达到输出转矩和负载转矩的平衡。

当电机处于力矩模式时，在t=0 s时，电机的转速恒定为 1 500 r/min，初始负载转矩为20 Nm;在t=0.25 s时，转矩突变为40 Nm。由图5（a）和（b）可以看出，当负载变化时，采用本文所提的电机控制方法，可以有效缩减转速和输出电磁转矩动态响应时间，抗扰动能力更强。对比图5（c）和（d）可以看出，当电机稳定运行时，MTPA控制方法的三相电流的最大值分别为10 A和17 A。当采用id=0控制方法时，三相电流的最大值分别为10.5 A和20 A。由此可见，本文所提的控制方法在稳态运行时电机输出的电流更小，能耗更低，电机输出效率更高。

5 结语

為了满足实际内置式永磁同步电机伺服系统转矩输出大、速度响应快、抗干扰能力强、电机输出效率高等要求，本文提出将自适应滑模控制方法应用在最大转矩电流比的控制中。采用牛顿-拉夫逊迭代法分配最大转矩电流比所需的交直轴电流，简化了计算方法，提高了方法的工程应用价值。速度调节器采用滑动模态控制方法，并针对鲁棒切换项设计自适应增益函数，有效降低了滑模的抖振，提高了系统的稳定性。仿真实验结果表明，该系统鲁棒性强，具有良好的动态性能和抗扰动能力，适用于永磁同步电机伺服系统的多种场合。

[参考文献]

[1] 黄鹏，苗长云，黄雷，等.参数在线估算的永磁同步电机最大转矩电流比控制[J].煤炭学报，2011，36（1）：172-176.

[2] 廖勇，伍泽东，刘刃.车用永磁同步电机的改进MTPA控制策略研究[J].电机与控制学报，2012，16（1）：12-17.

[3] 崔家瑞，高江峰，张波，等.永磁同步电机滑模变结构鲁棒控制[J].电机与控制学报，2016，20（5）：84-89.

[4] 高雅，刘卫国，骆光照.基于dSPACE的新型双滑模PMSM控制方法[J].中南大学学报（自然科学版），2015（6）：2036-2043.

[5] 李鹏飞，严欣平，苏盈盈，等.基于永磁同步电机逆系统解耦模糊滑模控制[J].太阳能学报，2011，32（4）：565-570.

[6] 李军，余家俊.基于分段曲线拟合的IPMSM最大转矩电流比控制研究[J].四川大学学报（工程科学版），2012，44（Z1）：307-311.

[7] 谢涛，高桂革，王杰.基于滑模控制器的PMSM的矢量控制系统研究[J].电机与控制应用，2018，45（3）：6-10.

收稿日期：2021-02-01

作者简介：葛晨阳（1994—），男，江苏兴化人，硕士研究生，助理工程师，研究方向：智能电网与控制技术。