基于高阶图卷积网络的城市空气质量推断模型*

陈 杰 ，许镇义 ，2

(1.中国科学技术大学 自动化系，安徽 合肥230026；2.合肥综合性国家科学中心人工智能研究院，安徽 合肥230088)

0 引言

近年来，随着经济的增长，环境问题也变得日益突出， 大气污染问题正受到前所未有的关注和重视[1]。城市空气中，如一氧化碳(CO)、碳氢化物(HC)、氮氧化物(NOx)、固体颗粒物(PM2.5、PM10)等污染物浓度与人们的身体健康息息相关[2-3]。 空气质量指数(Air Quality Index，AQI)是定量描述空气质量状况的指数，其数值越大说明空气污染状况越严重，对人体健康的危害也就越大[4]。

为了及时准确地反映空气质量及发展趋势，需要精确的空气质量监测设备。然而这些监测设备的建设成本以及后期的维护费用是昂贵的[4]，所以，在一个城市不同区域安装大量的空气监测设备是不现实的。 例如，北京市主城区面积约为1 381 平方公里，仅仅包含17 个空气监测站点，各个监测站位置分布由图1 所示。

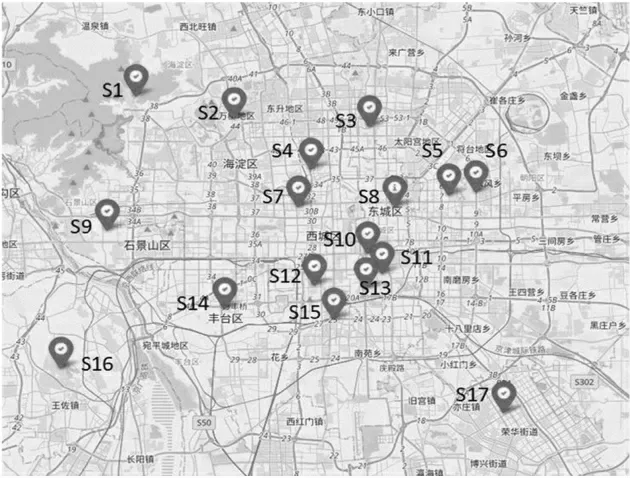
图1 北京市空气质量监测站位置分布

这些年来，关于空气质量推断的研究主要分为：基于知识驱动和基于数据驱动的两类方法。 基于知识驱动的方法主要使用数学模型[5-6]和物理知识[7]，模拟空气污染物的实际物理扩散过程，通过计算仿真来推断未观测区域的空气质量分布。 这些方法都采用了一系列优化技术，如相关性分析、聚类分析和多目标优化[8-10]。 为了达到稳定状态，仿真过程不仅需要复杂的系统编程，而且会消耗大量的计算能力。 模型简化和稳定性假设，也会使模型效率进一步降低。

近几年来，基于数据驱动的方法也在不断发展,并在空气质量推断方面取得了很好的效果。ZHENG Y 等[4]提出了一种基于Co-training 协同训练框架[11]的半监督学习方法来推断城市空间细粒度的空气质量。 但是该框架由两个独立的分类器组成，很难捕获不同特征之间的复杂交互性。CHEN L等[12]采用K-近邻策略来构建外部数据源(如路网结构、交通等)与空气质量分布之间的关系。 然而K的具体数值没有确切的理论标准，最近的K个站点的特征不一定是最有效的，并且不同站点的影响程度可能会随时间而变化，因此有可能导致出现非一致性的问题。 HSIEH H P 等[13]基于图标签节点传播[14]，设计了一种基于亲和关系的空气质量推断模型(the Affinity-based AQI Inference Model，AQInf)。 然而由于其自身模型性能的限制，AQInf 很难捕获图节点之间的反映空气质量时空变化趋势的关联程度。

本文主要想解决的问题是：如何基于城市已建立的有限数量的空气质量监测站，来精确地推断未监测区域的空气质量分布。 因而将城市空间细粒度空气质量预测问题转化为城市时空图(Spatio-Temporal Graph，STG)预测问题，其中，时空图中的每个节点表示城市中的每个子区域(1 km×1 km)，并且每个节点关联随时间变化的空气质量数值。 任务的挑战性主要基于以下几个方面：

(1)空气质量分布受到很多复杂的外部环境因素的影响(例如天气、交通、土地用途等)。 对于商业中心等交通流量大的区域，空气质量往往比公园湖泊等区域差。 这样会导致由于地理因素影响而出现不光滑数据值，很难通过基于插值的方法来精确推断未监测区域的空气质量。 例如，图1 中的S5、S6监测站点和S11、S13 监测站点，在地理位置上很接近，但是PM10、AQI 指数分布却常年差异很大，具体分布如图2 所示。 造成这个现象最可能的原因是，空气质量较优的站点，靠近公园或者湖泊，而空气质量较差的站点，处于商业中心或主干道附近，交通量较大。

(2)空气质量分布具有时空交互性。 在同一时刻内， 不同空间区域内的空气质量分布相互影响；在同一空间内，相同节点在不同时刻的AQI 数值相互关联。

1 问题描述

1.1 城市时空图

基于城市地理信息，将该城市区域划分成不相交的网格(1 km×1 km 的子区域)，并且每一个网格与随时间变化的AQI(Air Quality Index)相关联，如图3 所示。

将每个划分的网格看作一个节点，构建时空图G=(V；ε；A)，其中，V是节点的集合，|V|=N；ε 是边的集合，表示节点之间的连通性；A∈Rn×n为图G 的邻接矩阵。 时空图中，V可以表示为V=L∪U，其中，L表示为已建立空气质量监测站的节点集合，U表示为未建立空气质量监测站的节点集合。将L中的节点作为标签节点，U中的节点作为未标签节点。时空图的空间相关性通过同一时刻下节点之间的地理距离特征来反映，时间相关性通过同一节点相关联的不同时刻AQI 数值来反映。

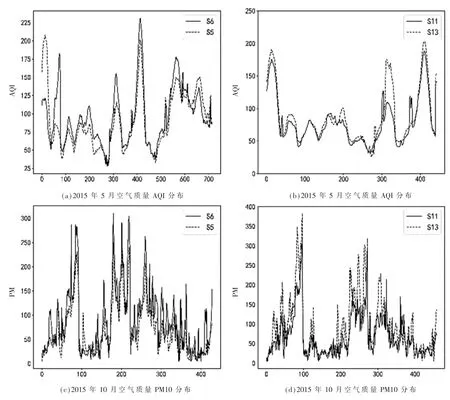
图2 不同监测站点的PM10，AQI 实时分布

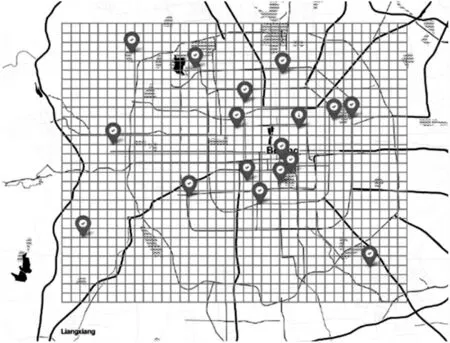
图3 城市区域网格划分

1.2 数据收集

收集与空气质量分布相关的外部影响因素，该外部影响因素主要包括气象数据、子区域POIs(Pointof-Interests)数目以及区域路网信息(如各区域高速路长度，主干道长度等[15]。 这些数据特征集合表示为F={f1，f2， …，fm}，fm表示收集到的第m个特征。POIs 类型如表1 所示。

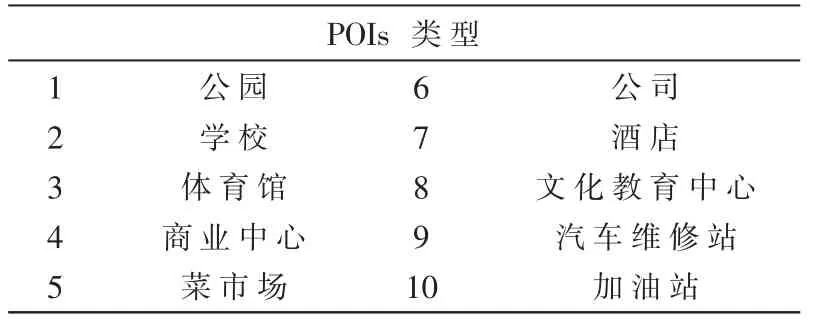
表1 POIs 类型列表

1.3 空气质量分布预测问题

问题：在{Ti|i=1，2，…，n}时刻，基于时空图G=(V；ε；A)，利用已观测区域节点L的空气质量分布fl∈R|L|×P来预测任意未观测区域U的空间细粒度空气质量分布fu∈R|U|×P。 空气质量分布预测任务主要是学习一个函数F(·)，将输入fl∈R|L|×P映射到输出fu∈R|U|×P：

其中，|L|为标签节点的数目，|U|为未标签节点的数目，P是每个节点特征的数目。

2 研究方法

2.1 图卷积网络

通用化卷积神经网络以处理任意图结构数据是近些年来研究的热点之一。BRUNA J 等[16]通过将滤波器和信号转换到傅里叶域，然后将相乘结果返回离散域从而实现图卷积。 信号变换是通过与图拉普拉斯图的特征向量相乘来实现的，需要对称拉普拉斯算子的二次特征分解。 然而，特征分解的低秩近似可以使Chebyshev 近似多项式来计算以降低计算复杂度[17-18]。 KIPF T N 等[19]通过局部频谱滤波器的一阶近似，设计了一种图卷积网络用于半监督学习。

作为图卷积的典型应用，SUN J 等[20]设计一种多视图图卷积网络用于预测城市不规则区域人群流量。 XU Z 等[21]设计一种时空图卷积多融合网络用于城市机动车排放预测。 CUI Z 等[22]设计了一种交通高阶图卷积循环神经网络，用于交通学习和预测。

2.2 高阶图卷积网络的设计

最近的一些研究[23-25]表明，对于图节点半监督学习， 用随机游走统计来学习表示的效果比较好，因为这样可以保留图结构的完整性。 在特殊条件下，如果图卷积网络的第一层激励函数是一个恒等函数，那么文献[19]中的GCN 模型也可以学习随机游走。 假设第一层的激励函数是一个恒等函数，即：

该GCN 模型可以进一步简化为：

可以发现，在特定条件下的GCN 模型实际上做了一步随机游走，可以将节点的信息传递到高阶邻居节点。 然而在Eq.2 中，信息特征在图边之间的传递呈缩减状态(左乘标准化邻接矩阵Aˆ，输出经过了非线性激励函数σ(·))。 因此，不能在原来的多层GCN 网络上直接对Aˆ取高阶， 否则会导致网络性能下降。 提高图卷积网络的阶数，同时减少网络的层数，并将每阶网络提取的特征进行融合从而得到最终特征表示：

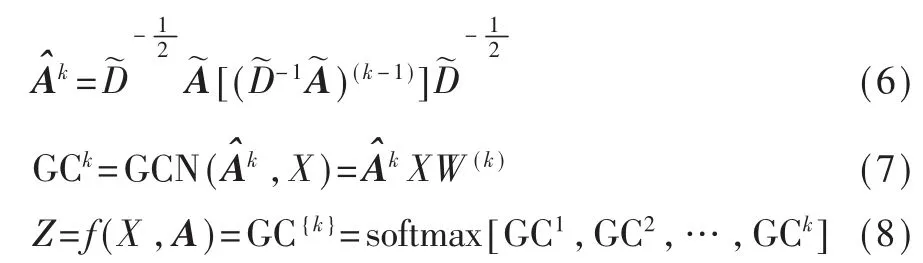
其中，W(k)为的权重参数，GCk表示图卷积网络提取到的k阶特征。

2.3 空气质量推断模型

首先定义时空图的高阶邻居矩阵，时空图的一阶邻居矩阵即为邻接矩阵A，K阶邻接矩阵可以通过A 的k次幂得到。 如图4 右边所示，一个节点(五角星)的K阶邻居节点为图中的黑色边可以到达的节点。

将高阶图卷积网络(High-order Graph Convolution，HGCN)应用到环境监测领域，并设计成空气质量推断模型(Air quality inference model based on High-order Graph Convolution，HGCNInf)，其中，HGCN 用来捕获空气质量分布的时空交互性，全连接神经网络(Fullyconnected Neural Network，FNN)用来提取复杂的外部影响因素特征，具体框架如图4 所示。 为了使模型更具有合理性和解释性，将Eq.7 的K阶卷积操作修改为如下形式：

图4 空气质量推断模型框架(图的右边为高阶图卷积网络构图)

将图卷积提取的K阶特征连接在一起，定义如下：

GCk∈RN×(K×P)是图卷积网络提取的K阶特征集合，这样就达到了提取输入数据高阶特征的目的。将GCk∈RN×(K×P)通过全连接网络ffc1，通过反向传播共同训练。 定义如下：

其中，空气质量分布特征GC ∈RN×P，可训练参数Wfc1∈RP×(K×P)。

然后用全连接网络FNN 来捕获外部影响因素特征，定义如下：

其中，fm∈RN×M为M个外部影响因素，可训练参数Wfc2∈RP×M，GCf∈RN×P。

将外部影响因素特征GCf∈RN×P与空气质量分布特征GC∈RN×P进行融合：

其中，可训练参数Wfc3∈RP×P，得到总特征GCall∈RN×P。

进一步，得到未标签节点的AQI 分布Fu：

其中，Fl∈R|L|×P为标签节点的空气质量分布输出，Fu∈R|U|×P为未标签节点的空气质量分布输出。

2.4 网络损失和训练

最小化模型的输出Fl和已知训练标签Y的交叉熵损失，交叉熵损失定义如下：

其中，*表示哈达玛积；diag(Vl)表示一个对角阵，该对角阵的元素，当(i，i)∈Vl时，设置为1，其余元素为0。

为了使图卷积特征更具有稳定性，在损失函数上面增加正则化项。 相邻节点对特定节点的影响必须通过两节点之间的所有节点传递，图卷积操作提取到的不同阶节点特征不应该有太大变化。 为了限制相邻阶特征之间的差异，将基于L2 范数的卷积特征正则化项添加到损失函数中。 定义如下：

总的损失函数如下：

其中，参数α 用于控制正则化项的权重大小。 最小化模型损失函数对网络进行训练：

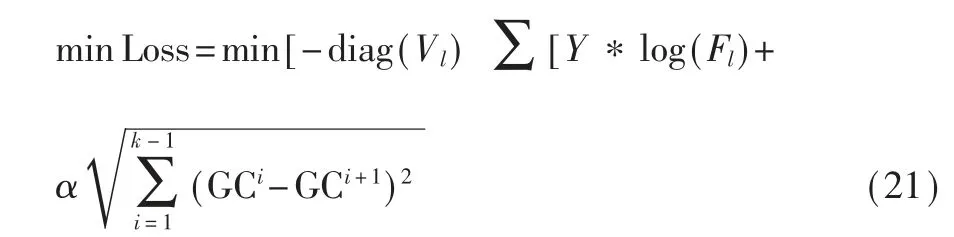
当网络训练结束时，从其未观测区域的AQI 分布Fu中找到量化概率最高的值，并定义为未标签节点的AQI 预测值：

3 实验结果

3.1 数据描述

采用北京市空气质量AQI 实时数据验证了提出的模型， 该数据收集于北京市生态环境监测中心，每小时收集一次，时间跨度从01/01/2015 到12/31/2015，包含17 个监测站点，总计共17×8 760 条数据。 在实验中，将北京主城区划分成30×38 个网格子区域(1 km×1 km)，其中17 个子区域建有空气质量监测站，剩余的1 123 个子区域的空气质量分布未知。

3.2 数据处理

本文的输入数据主要包含北京市空气质量数据和复杂的外部影响因素数据。 采用one-hot 编码来处理空气质量AQI 数据，采用Z-Score Normalization将外部影响因素数据进行线性变换，使其结果映射到[0，1]范围内。 北京城市时空图的邻接矩阵根据节点间的距离，通过阈值化高斯核加权函数[26]来计算，计算公式如下：

其中，dist(pi，pj)2表示节点pi和pj之间的欧式距离，σ2和ε 是阈值用来控制矩阵Wij的分布和稀疏性。本实验中，σ2和ε分别设置为10 和0.05。

3.3 实验设置

3.3.1 实验评价指标

为了评价和比较不同模型之间的性能，采用两个常用的指标： (1)Mean Absolute Percentage Error(MAPE)；(2)Root Mean Squared Error(RMSE)。

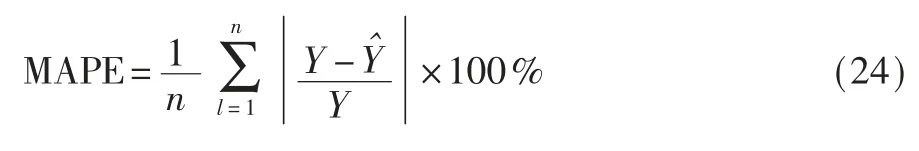
3.3.2 基准模型

通过以下基准模型和提出的模型进行了比较：

SVR：Support vector regression[27]。 SVR 利 用 监 测站点的历史数据作为训练数据用来预测未标签节点的空气质量数值。

AQInf：Affinity-based AQI inference model[13]。 对于城市空气质量预测而言，基于目前的知识，这是最先进的方法。 利用标签节点的历史数据，结合外部影响因素，用来预测未标签节点的空气质量分布。

GCNInf：GCN-Based AQI inference model。 设计了一个如文献[19]所描述的两层图卷积网络。 类似于AQInf，利用标签节点的历史数据，结合外部影响因素，用来预测未标签节点的空气质量分布。

所有的神经网络模型实施都是基于Pytorch version：1.1.0， 并且评价和训练都基于CPU Intel®CoreTMi5 -4210U CPU@1.70 GHz，NVIDIA GeForce 840M。

3.4 实验结果分析

在实验中，由于仅仅具有标签节点(已建立空气质量监测站的子区域)的真实数据，对于未标签节点(没有建立监测站的子区域)而言，没有真实数据可以验证空气质量推断模型的精度。 因此，采用交叉验证的方法，在17 个标签节点中随机选择12个节点作为训练节点，产生12×8 760 个训练数据，剩余的5 个标签节点用来作为验证节点，产生5×8 760个验证数据。

3.4.1 训练效率

考虑不同卷积阶数K对所提出来的HGCNInf推断性能的影响。 图5(a)、图5(b)和表2 是HGCNInf模型取不同阶数的性能比较。 对于北京市空气质量分布数据而言，在两个指标MAPE 和RMSE 上，当高阶图卷积网络阶数K=3 时，模型HGCNInf 的推断性能最好。 图5(c)和表3 为HGCNInf 网络取不同阶数时，在每个时刻训练1 000 次所消耗的平均时间，可以发现，随着HGCNInf 卷积网络阶数的增加，训练时间也随之增加；此外，当模型HGCNInf 考虑外部影响因素后，训练所消耗的时间将大幅度增加。

3.4.2 空气质量推断模型结果对比

综合模型预测精度和时间效率，选取K=3 作为HGCNInf 的阶数，其预测精度如表4 所示。

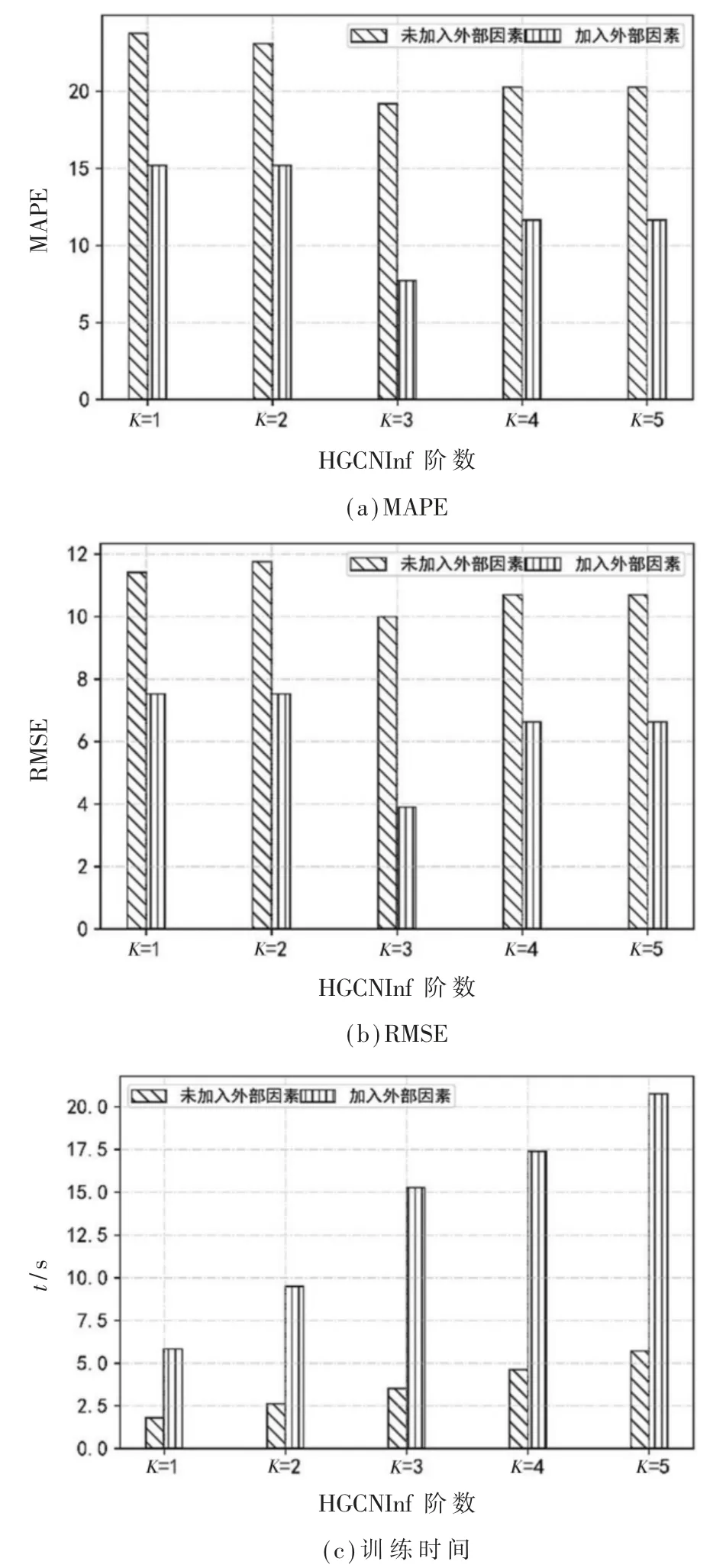
图5 不同阶数的HGCNInf 性能和训练时间

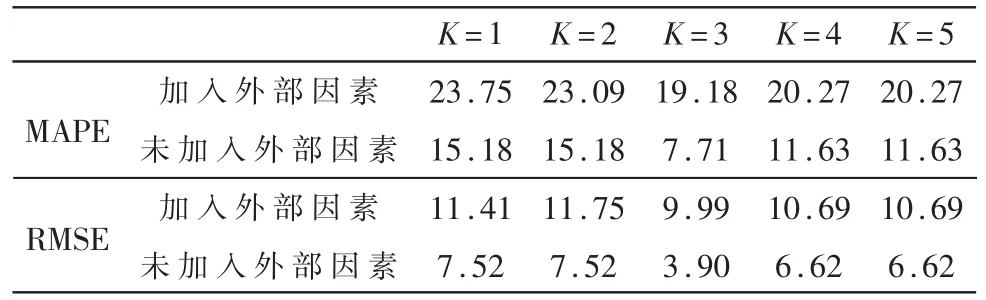
表2 不同阶数的HGCNInf 性能比较(%)

表3 不同阶数的HGCNInf 训练时间(s)

表4 空气质量推断模型的性能比较(%)

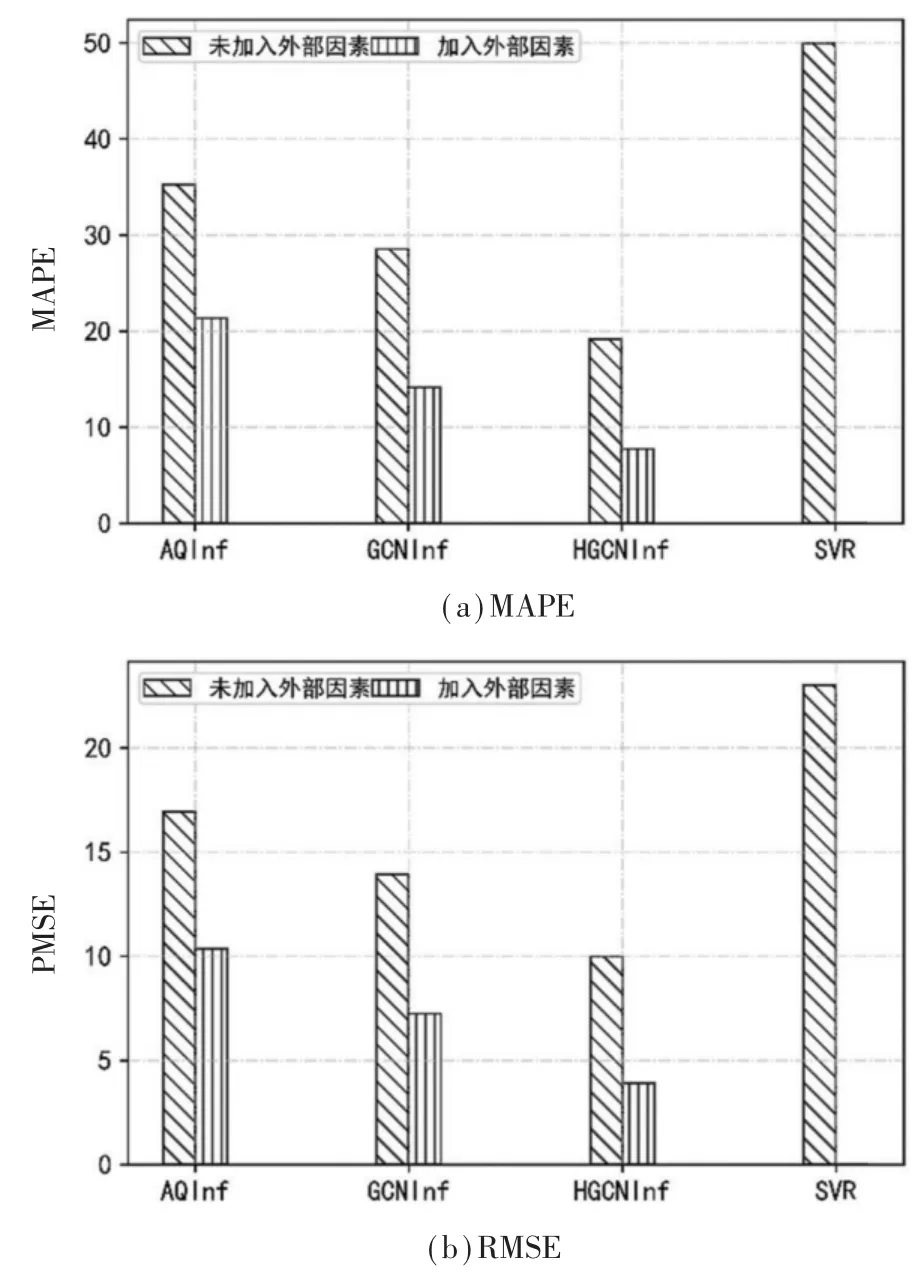
图6 空气质量推断模型的性能比较

对各个空气质量推断模型分别训练三次，每次训练10 000 次，然后取平均值作为最终结果。 表4和图6 展示了提出的模型HGCNInf 和其他基准模型在北京市空气质量分布上两个指标的评价对比。 可以发现， 提出的模型HGCNInf， 无论在指标MAPE上,还是指标RMSE 上，都远远优于其他基准模型。另外，对比空气质量推断模型在未加入外部影响因素和已加入外部影响因素在两个评价指标上的差异，同样的模型，在考虑了外部影响因素影响后，对于城市空气质量分布预测精度的提升有着显著的作用。因此，可以得出结论，复杂的外部影响因素与空气质量分布息息相关，这也很好地解释了图1 中地理位置很接近的监测站点，在空气质量数值上却常年差异较大的现象。

3.4.3 空气质量推断模型的鲁棒性

为了测试各个空气质量推断模型对标签节点数目的敏感性，随机丢弃相同的标签节点，观察各个空气质量推断模型预测性能的变化程度，具体结果如表5 和图7 所示。

从表5 和图7 中可以发现，当逐渐减少标签节点的数目时，所提出的模型HGCNInf 的预测精度在评价指标MAPE 和RMSE 上总是优于各个基准模型， 并且MAPE 和RMSE 增长速度相对缓慢。 这样的结果表明，模型HGCNInf 的鲁棒性要远远优于各个基准模型， 即使当只有非常少的标签节点可用时，模型HGCNInf 也同样是适用的。

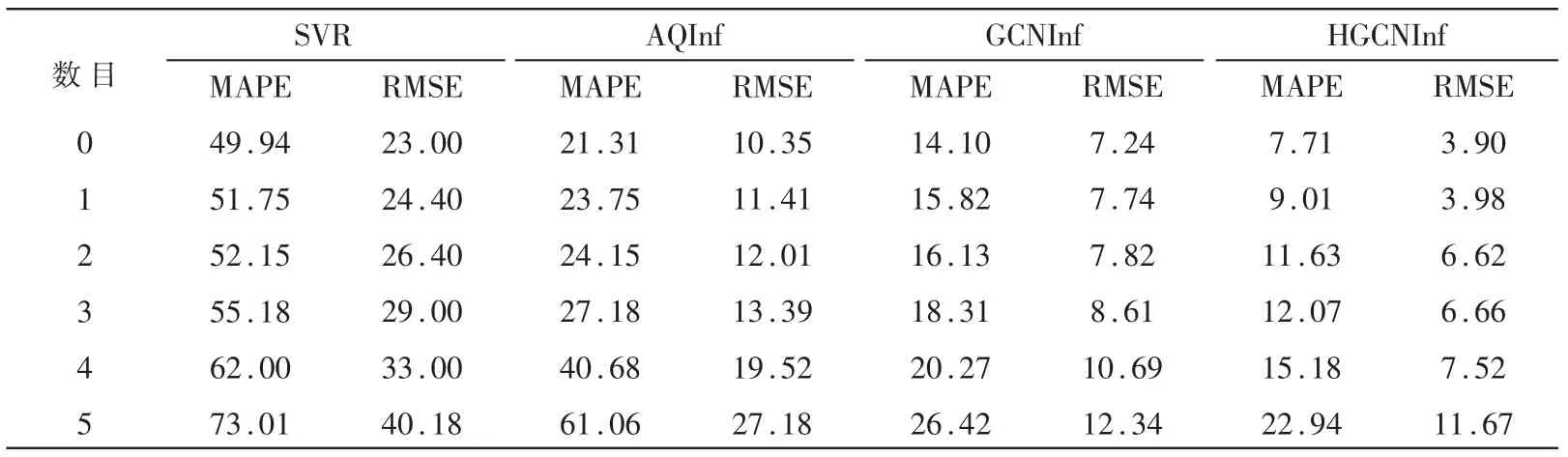
表5 空气质量推断模型的鲁棒性(%)

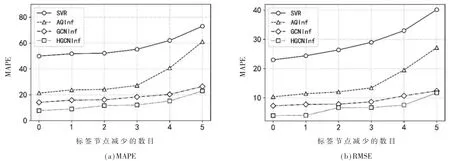
图7 空气质量推断模型的鲁棒性

4 结论

本文将城市空间细粒度空气质量预测问题转化为时空图预测问题，基于改进的高阶图卷积网络设计了一种有效的空气质量推断模型HGCNInf。HGCNInf 不仅可以捕获大气污染物分布的时空相互作用，还可以提取复杂的外部影响因素特征，从而可以准确地预测整个市区的细粒度空气质量分布。在接下来的工作中，将专注于通过并行化提高该模型的效率。此外，未来将寻求模型的更多应用，特别是在城市地区的空气质量监测站布点智能化选址领域。