基于TCN的时序数据研究

翟剑锋

（中国社会科学院大学计算机教研部 北京市 102488）

时序数据是以时间为先后顺序，记录各个时间点观测值的数据序列，反映了事物的发展变化规律。通过对时序数据进行建模分析，寻求新的预测模型和方法，探究数据的变化规律，提高时序数据预测的准确性，一直是学者的研究热点。时间序列分析在工程、金融、科技、生产生活等众多领域有着广泛的应用。通过将时间序列分析与机器学习相结合，可以更好的应用于数据检测、预测等场景。本文采用时序卷积神经网络对时序数据进行分析及预测，并在太阳黑子数据集上进行验证，同时与传统的时序数据分析方法及长短时记忆网络LSTM 的时序预测方法进行类比。

1 相关工作

时间序列数据的分析，主要有传统的基于统计的分析方法和以机器学习为基础的的分析方法。随着计算机计算能力的不断提升及深度学习的发展，深度神经网络模型能够更好的捕获数据间的潜在关联信息以提高模型的预测精度，国内外研究人员逐渐将深度神经网络引入到时间序列数据的分析中来，成为当前研究的热点问题。

在早期的基于统计的分析方法中，Yule 和Walker 分别提出自回归（AR）模型和移动平均（MA）模型，用于预测市场的变化规律和大气规律，奠定了基于统计的分析方法基础，一直沿用至今。1970年，由Box 和 Jenkins 提出了自回归差分移动平均（ARIMA）模型，并验证模型的有效性。进入本世纪以来，针对多变量、异方差等问题，Engle 提出自回归条件异方差(ARCH)模型，解决了具有波动性的时间序列预测问题，Bollerslov 进一步放宽了 ARCH模型的约束条件，提出广义自回归条件异方差(GARCH)模型。Granger 提出了格兰杰协整定理，主要用于处理协整和误差修正模型二者之间的关系。

以机器学习为基础的分析方法中，包括支持向量机、随机森林、集成学习等方法。主要是利用数据的自身特征，建立从自变量到预测值的映射关系，并采用一定的优化算法对代价函数进行优化，从而建立模型。Wang 等[1]利用支持向量机，构建了基于机器学习的预测方法，在其文中平均预测精度可以达到95%以上，远超传统的统计研究方法。

随着神经网络的引入，杨怡等[2]将BP 神经网络和SARIMA组合对电力负荷数据进行分析模拟，大量的实验结果表明其方法的有效性，有效地提高预测准确度。孔江涛等[3]人利用循环神经网络（RNN）解决城市路线规划问题，能够较容易的获得多个最优路线。周扬等[4]引入长短时记忆神经网络模型（LSTM），并验证基于LSRM 的方法在化肥价格预测中能够获得较高的准确程度。Bao等[5]结合小波变换和LSTM 模型预测股票第二天的收盘价。Karim等[6]将注意力机制和LSTM 模型相结合，基于Attention 的LSTM模型进行时间序列分类，很大程度上提升了分类的准确性。

2 时序卷积神经网络

由于序列中的数据之间具有一定的相关性，即当前的序列输出不是独立的，与先前的输出之间具有一定的关联。循环神经网络（RNN）能够很好的将当前输出和先前输出联系起来，广泛的运行于自然语言处理、语音识别等领域。但随着网络深度的增加，RNN会出现梯度消失和梯度爆炸的问题。

长短期记忆神经网络（LSTM）是由RNN 扩展而来，具有称为“门”的内部机制，可以调节信息流，用来解决循环神经网络较难保持长时间记忆的问题。LSTM 通过细胞状态让信息能够在序列链中传递下去，同时通过“门”结构来实现信息的添加和移除操作，可以有选择的让遗忘信息或接受信息。但由于每一个LSTM 的细胞里面都包含有4 个全连接层，如果LSTM 的时间跨度很大，并且网络又很深，计算量会非常大，训练时间过程，同时LSTM 自身无法用于并行计算。

时序卷积网络（TCN）以卷积神经网络（CNN）模型为基础，由具有相同输入和输出长度的扩张的、因果的1D 全卷积层组成。TCN 模型中的卷积为因果卷积，层层之间具有因果关系，从而保证不会错失历史信息或未来数据的情况发生。另外TCN 可以将任意长度的序列映射到相同长度的输出序列，利用残差模块和扩张卷积，以更好地控制模型的记忆长短，并提升预测能力。

2.1 一维全卷积

TCN 利用一维全卷积（1-D FCN）的结构，每一个隐层的输入输出的时间长度都相同，维持相同的时间步，具体来看，第一隐层不管kerel_size 为多少，输入若是n 个时间步，输出也是n 个时间步，同样第二隐层，第三隐层……的输入输出时间步长度都是n。对于第一个时间步，没有任何历史的信息，TCN 认为其历史数据全是0，图1中kernel_size 为3。

2.2 因果卷积

和传统的卷积神经网络的不同之处在于，因果卷积不能看到未来的数据，它是单向的结构，不是双向的。也就是说只有有了前面的因才有后面的果，是一种严格的时间约束模型，因此被成为因果卷积。

因果卷积对于上一层t 时刻的值，只依赖于下一层t 时刻及其之前的值。即输出序列中的元素只能依赖于输入序列中在它之前的元素。为了确保一个输出与输入具有相同的长度，需要进行零填充。如果只在输入数据的左侧填充零，那么就可以保证因果卷积。假设输入序列的右边没有填充，它所依赖的最后一个元素就是输入的最后一个元素。现在考虑输出序列中倒数第二个输出元素。与最后一个输出元素相比，它的内核窗口向左移动了1，这意味着它在输入序列中最右边的依赖项是输入序列中倒数第二个元素。根据归纳，对于输出序列中的每个元素，其在输入序列中的最新依赖项与其本身具有相同的索引。图2展示了一个输入序列长度为4，kernel_size 为3 的示例。

在输入数据左侧填充为零的情况下，可以获得相同的输出长度，同时遵守因果关系规则。在没有扩展的情况下，维持输入长度所需的零填充的数量总是等于kernel_size- 1。

2.3 扩张卷积

卷积神经网络通过卷积计算形成记忆，感受野的大小反映了使用多少数据生成记忆。一个传统的卷积层在输出中特定的值取决于输入中kernel_size 个数据，假如kernel_size 为3，那么输出中的第5 个元素将依赖于输入中的元素3、4 和5。当将多个层叠加在一起时，这个范围就会扩大，图3将kernel_size 为3 叠加两层，得到的感受野大小为5。

一般而言，具有n 层且kernel_size 为k 的一维卷积网络的感受野r 为r=1+n*(k-1)。即感受野大小与卷积核大小、卷积层数呈线性关系。因此，增加卷积层以及增大卷积核均能扩大感受野。在保持层数相对较小的情况下，增加感受野大小的一种方法是向卷积网络引入扩张系数。扩张系数是指输入序列的元素之间的距离，该元素用于计算输出序列的一个值。因此，传统的卷积层可以看作是膨胀值为1 的扩张层，图4展示一个扩张系数为2 的扩张层的示例，其输入数据长度为4，kernel_size 为3。

扩张卷积的计算公式定义为：

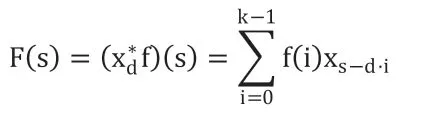
式中，d 表示扩张系数，k 表示卷积核大小。当 d 为1 时，扩张卷积退化为普通卷积，通过控制 d 的大小，从而在计算量不变的前提下拓宽感受野。

如果多从叠加的卷积层的扩张系数相同，可能使得部分时刻数据没有参与计算。这个问题可以通过在层中向上移动时，d 的值呈指数增加来解决。定义一个扩张基数b，利用层数i 来计算特定层的扩张系数d，即d=bi。图5显示了一个网络，其中输入长度为10，kernel_size 为3，扩张基数为2，这将确保3 个扩张的卷积层完全覆盖。

3 实验结果与分析

实验数据集来自比利时皇家天文台网站(http://www.sidc.be/silso/datafiles) 发布的太阳黑子13 个月平滑月度数据。从1749年6月到2021年1月，共包含3265 组数据，其中2010年至2021年的数据为测试集，其他数据为训练集。

实验所使用的模型有ARIMA、LSTM、TCN，在尽量公平的前提下，LSTM 与TCN 的时间步均为120，具体参数设置如下：(1)ARIMA 分别取p=2，d=1，q=2；(2)LSTM 包含两个隐藏层，隐藏层单元数为50；(3)TCN 每层的扩张系数分别为［1，2，4，8，16，32］，每层卷积核个数均为32，卷积核大小为2。

为了评价模型的优劣，采用均方根误差(RMSE)为主要评价指标，用于测量实际值和预测值之间的差异或残差，三个模型的均方根误差值分别为50.24，34.62 和28.36。

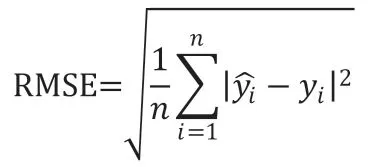
从评测结果可以看出，相对于其他对比模型，TCN 预测效果最好，在RMSE 指标上最低。LSTM 能获取数据序列的时序关系，预测效果优于传统的ARIMA 模型，但不如TCN 模型。

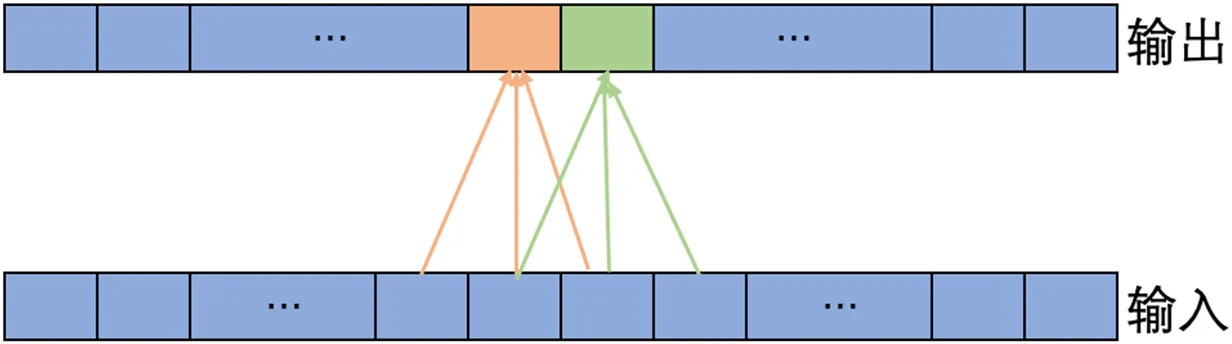
图1：一维全卷积简图

图2：因果卷积

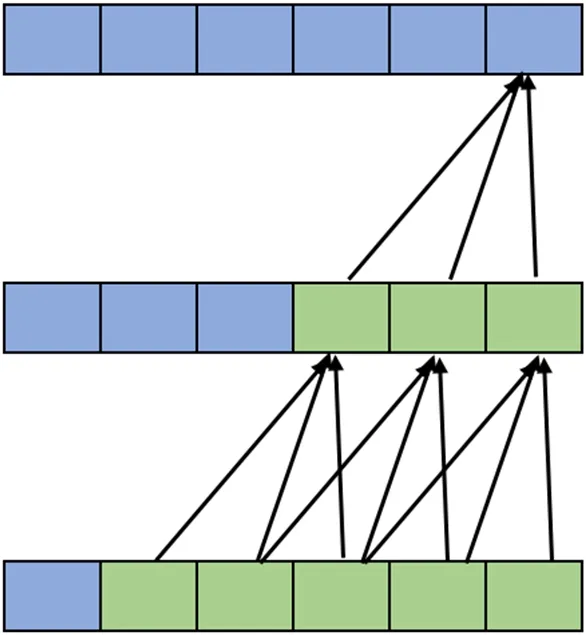
图3：感受野

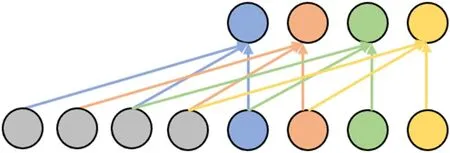
图4：扩张卷积

图5：扩张系数

4 结束语

本文研究时间卷积网络的基本思想，并将其应用于太阳黑子数据集上进行预测，同其他相关模型进行验证类比。TCN 由6 层卷积层堆叠而成，每层通过Padding 的方式实现因果卷积，扩张系数逐层呈指数增长。指数增长的扩张系数使得模型可以获取序列的长时记忆。实验结果表明，TCN 算法预测效果优于LSTM，证明了运用时间卷积神经网络进行时序数据分析的可行性。