基于ADAMS和ANSYS Workbench的AGV剪叉式升降机构的仿真分析研究
徐恒才, 李鹭扬
(扬州大学 机械工程学院,江苏 扬州225127)
0 引言
随着科技的不断发展,AGV开始广泛应用于各领域,提升机构作为AGV不可或缺的一部分,发挥着极其重要的作用。提升机构与AGV是一个整体结构,所以对提升机构的尺寸和稳定性有所要求。现有机构中,AGV提升机构普遍具有结构复杂、自身质量较大、稳定性弱等缺点,为了解决这些问题,剪叉提升机构开始进入人们的视野[1],但是一些剪叉式的提升机构在提升的时候载物板的重心会发生偏移,向一端转移,因此不适合质量分布不均的载物场合;还有一些剪式提升机构中虽然解决了重心偏移的问题,但是驱动单元是伴随提升机构升降的,这就意味着升降机构在举升的同时还要承载电动机的重力,并且电动机随升降机构升降就意味着电动机的线路也要随之上下运动,这样对电路损坏极大;提升机构的驱动单元采用液压或者电缸,这就导致提升机构会比较大、比较笨重,从而导致AGV整体尺寸变大,不适合在AGV上应用;其他一些提升机构结构复杂,不便于后期维护。
针对以上问题,设计了一种剪叉式AGV提升机构,包括固定底板、两个升降组件、升降板和驱动部件,解决了结构复杂不可靠的技术难题,结构简单,工作可靠,具有广阔的市场优势和前景。本文利用SolidWorks软件进行参数建模,并通过仿真软件ADAMS和ANSYS Workbench进行虚拟仿真分析,得到相关技术参数,为产品设计和优化提供参考和数据支持[2]。
1 仿真虚拟样机的建立
1.1 模型建立与简化
本研究设计的AGV剪叉式升降机构的基本参数如下:举升托板尺寸为500 mm×300 mm,提升高度行程至少为80 mm,剪支杆长为200 mm,采用SolidWorks软件建立模型。将举升托板的上表面至车架底板的上表面的距离调至140 mm,将装配好的三维模型导入到ADAMS中。
1.2 定义特征
将简化之后的机构,丝杆螺母的材料定义为轴承钢,密度为7.81 g/cm3,其它材料全部设置为铝合金,密度为2.74 g/cm3。AGV最大负载为100 kg,定义整个环境为理想状态,在举升托板的几何中心施加一个竖直向下100 kg的载荷。利用布尔和操作将车架底板、升降组件、滑轨组件、升降托板合为一体,然后根据实际运动状态添加相应的运动副及约束。
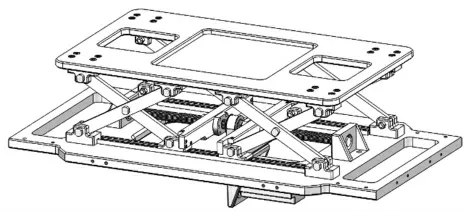
图1 升降机构三维模型图
2 剪叉升降机构仿真分析
2.1 升降机构丝杆螺母和托板运动学仿真分析
2.1.1 添加驱动
定义仿真的剪叉式升降机构托板上升和下降过程的行程至少为80 mm,为了更好地模拟仿真其运动过程,定义升降托板运动过程为:0~1 s加速,1~4 s匀速,4~5 s减速,最大速度即匀速阶段设置为20 mm/s,整个上升过程时间为5 s,现对托板升起过程进行运动学仿真分析,设置运动函数为
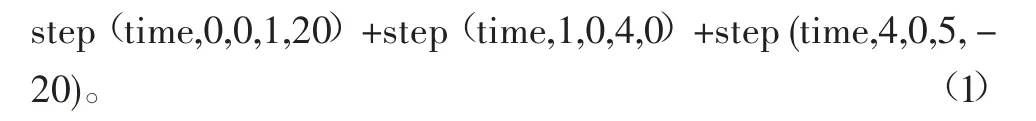
2.1.2 仿真分析
运行仿真使升降机构上升到工作高度并停止,得仿真变化曲线图,如图2~图5所示。
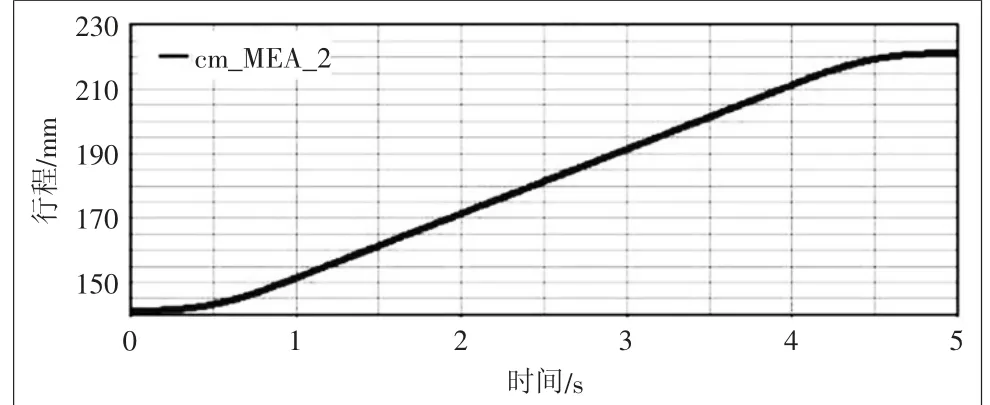
图2 升降托板行程
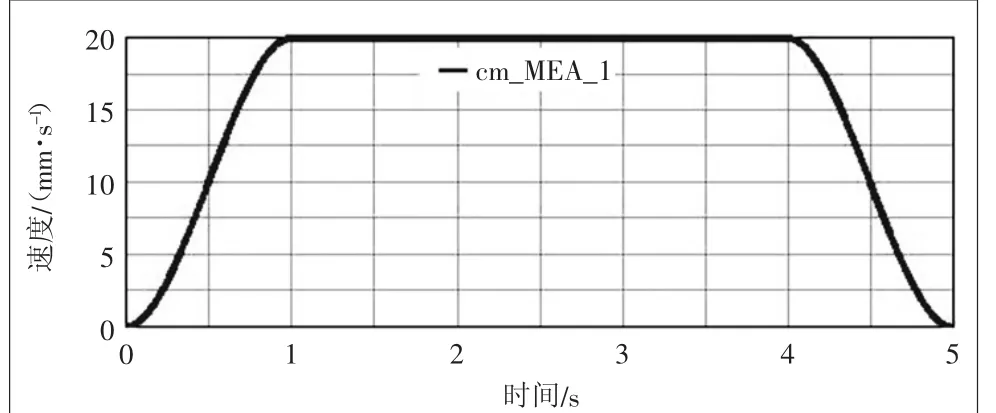
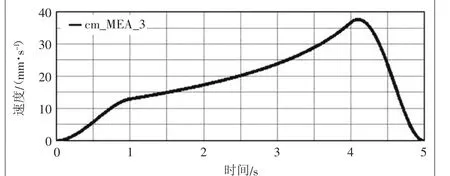
图4 升降机构丝杆螺母前进速度变化曲线
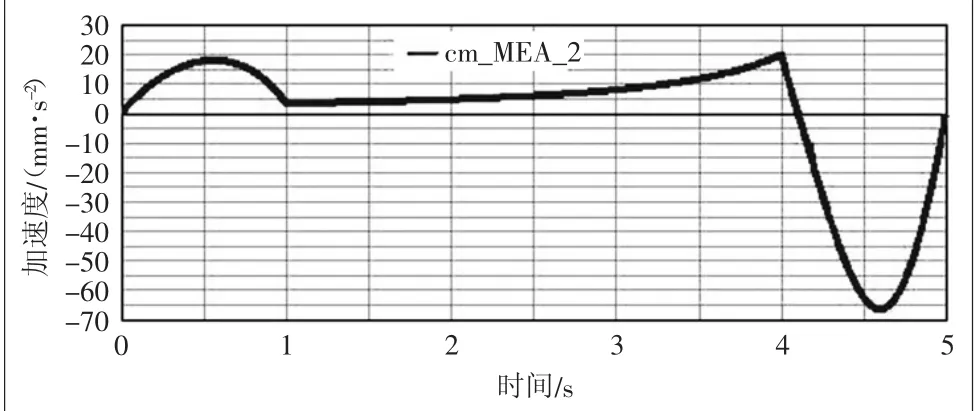
图5 升降机构丝杆螺母运动加速度变化曲线
从图2中得出托板的运行高度轨迹为141.4545~221.4545 mm,行程为80 mm,符合设计要求。从图4可以看出,升降机构在运行过程中丝杆螺母带动推杆前进的速度不断增加,在4.1 s左右达到峰值37.7043 mm/s,结合图5加速度曲线图可以看出,在0~4 s之间(即加速和匀速阶段),螺母最大加速度为20.2167 mm/s2,4~5 s减速阶段达到减速峰值66.2602 mm/s2,符合实际工况。
此仿真得到了升降机构丝杆的转速,进而可以得到电动机所需的转速,最终得到升降机构所需的控制程序。图3表示设定的初始条件,可以确定软件在初始条件设置的step函数的正确性。通过Adams仿真分析得到丝杆螺母的前进速度(如图4),从而可以间接通过公式计算出丝杆的转速,计算公式为

式中:V为丝杆转速;V1为丝杆螺母速度;d为丝杆导程。
得到丝杆的转速,即可根据齿形带的传送比确定电动机的转速,进而可以根据以上数据信息得到升降机构控制程序。
2.1.3 确定丝杆转速
在上述的仿真中已经得到丝杆螺母的前进速度曲线,现定义丝杆的导程d为4 mm。得到丝杆的转速曲线,如图6所示。
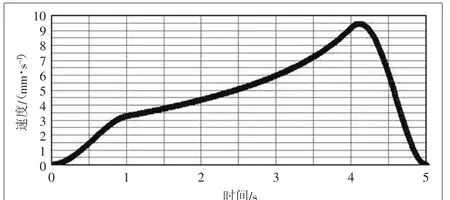
图6 丝杆转速曲线
由图6升降机构丝杆的转速曲线,即可得到升降机构电动机的转速,从而获取控制程序所需的数据参数,完成升降机构的整体控制,计算公式为

式中:n为电动机转速;n1为丝杆转速;i为传动比。
2.2 升降机构受力分析
2.2.1 添加驱动
运用Adams中motion调用外规划数据SPLINE驱动,将已经仿真出的丝杆螺母运动速度变化曲线导入到Adams中作为螺母运动的驱动。
2.2.2 仿真分析
仿真获得导轨耳座、固定耳座、两者间角度α变化的曲线图,如图7~图11所示。
根据图7可以看出,升降机构的推杆在初期水平受力最大为460.85 N,随着托板的上升推力逐渐减弱,最终达到95.64 N,这为丝杆螺母副和电动机的选型、推杆的安装方式提供了依据。图8和图9表示的是导轨耳座和固定耳座在垂直方向所受的力,从图中可以看出,在0~2.5 s期间,两者受力趋于平稳,分别在300 N和40 N附近,到2.5 s开始出现突变,在3.7 s分别达到最大最小值,这为优化升降剪支机构提供了参考依据。图10表示的是导轨耳座竖直方向的受力随角度α变化的曲线,可以看出α=91°时受力最大为298.2547 N,在α=70°时受力最小为188.4809 N。图11表示的是其水平方向所受的力与其角度变化,随着时间的增加,水平受力在逐渐减小。图10和图11仿真结果符合实际工况,将每个α角度、导轨耳座受力情况表达出来,可以为导轨、滑块和推杆的设计、选型和优化提供直观的数据支持。
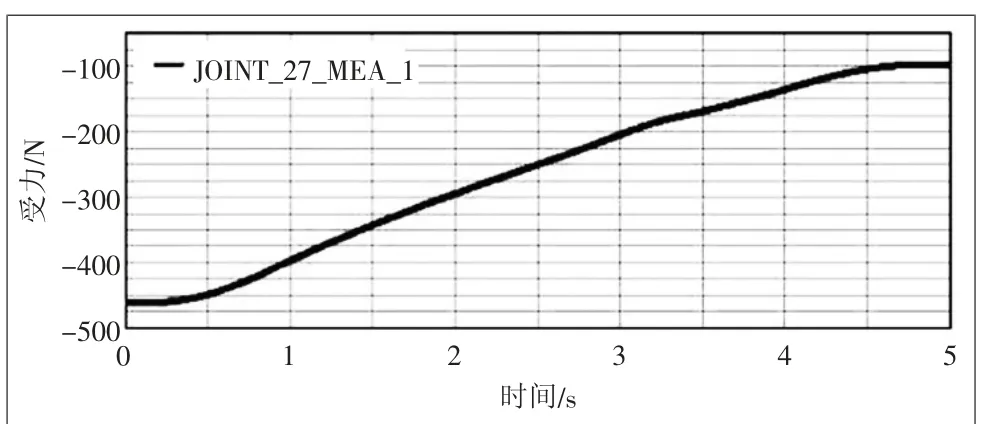
图7 导轨耳座X轴受力变化曲线图
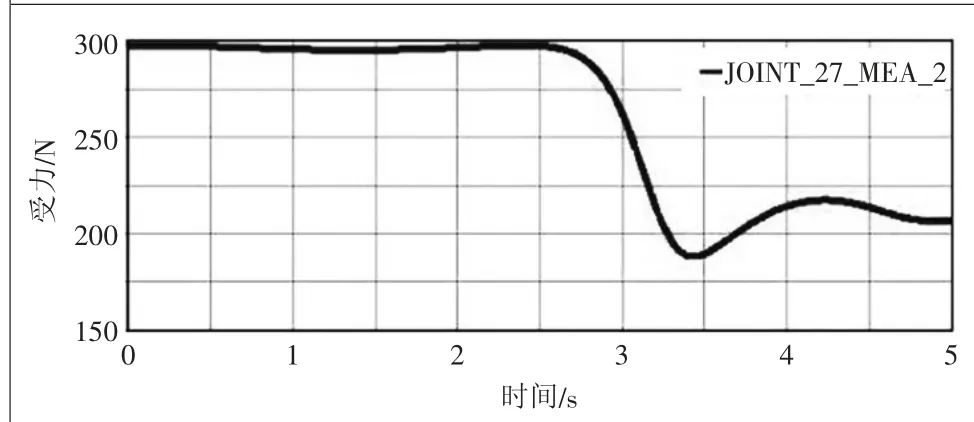
图8 导轨耳座Y轴受力变化曲线图
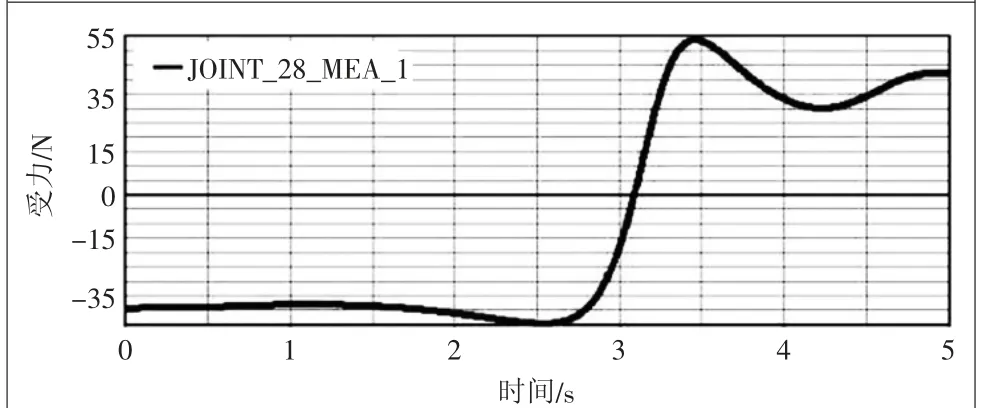
图9 固定耳座Y轴受力变化曲线图

图10 导轨耳座Y轴受力随角度α变化曲线图
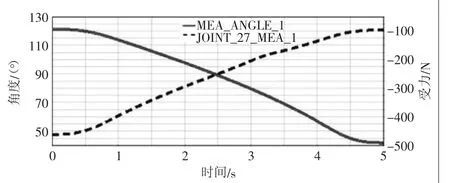
图11 导轨耳座X轴受力与角度α随时间变化曲线图
3 升降机构驱动部件有限元仿真
3.1 材料属性的定义与网格的划分
将升降机构的驱动部件的三维模型导入到ANSYS Workbench软件中,建立新材料轴承钢GCr15,其材料参数为:弹性模量为219 GPa,泊松比为0.3,密度为7.81 g/cm3,屈服强度为518.42 MPa。
3.2 静力学仿真
根据实际工况,在模拟部件添加相应的约束条件。根据前文2.2节中的受力分析得到推杆两端水平受力为460.85 N,由受力平衡条件在螺母内孔壁施加一个反向作用力,力的大小为921.7 N。得到求解的云图,如图12~图16所示。

图12 总变形

图13 等效应变

图14 等效应力

图15 最大主应力

图16 最大剪切应力
根据图12所示云图,得出最大变形量为6.2659×10-2mm,发生在推杆的中心位置;最大等效应变为4.6543×10-4mm(如图13),最大等效应力为38.551 MPa(如图14),最大主应力为34.875 MPa(如图15),最大剪切应力为20.892 MPa(如图16),都发生在推杆两端单独一处螺纹孔处,其次应力大小的位置在导轨滑块上表面与推杆的接触位置周围,对应力最大点进行强度计算,计算公式为

式中:[δ]为许用应力;δ1为极限应力值;n为安全系数。
因为导轨滑块产生的摩擦力很小,可以忽略不计,为了避免其影响,更好地保证强度要求,现取安全系数为2。由于最大应力远远小于许用应力[δ]=δ1/2=259.21 MPa,所以模拟的机构满足强度要求[5]。
通过对升降机构的力学仿真,可以通过仿真后的求解云图很直观地得到仿真部件的最大受力点和最大变形点,即危险点,并可以通过相关的数据参数计算判断机构的强度特性,为机构初期的设计和后期的优化起到了关键作用。
4 结语
利用SolidWorks建模和ADAMS、ANSYS Workbench软件对升降机构进行仿真分析,在保证升降拖板设计要求的同时,仿真计算出此升降机构设计与优化所需要的关键数据,模拟仿真结果与实际工况一致。通过仿真分析,得到每组剪支杆之间竖直方向的角度在42.07°~121.46°之间变化,丝杆螺母最大前进速度37.7043 mm/s,导轨耳座竖直方向最大受力为298.25 N, 水平最大受力460.85 N。推杆最大变形量为5.4001×10-2mm,最大应力为34.93 MPa,危险点发生在推杆两端单独一处螺纹孔处,其次是在导轨滑块上表面与推杆的接触位置边缘周围。整个仿真过程可作为丝杆螺母副和电动机的选型、升降机构导轨等机构的设计和优化提供参考与依据,同时可以为升降机构的疲劳强度分析提供数据支持。

