基于LSTM 网络模型的航天器热变形预测

王 丁， 罗文波， 吴 琼， 赵震波， 王云锋

（1.北京空间飞行器总体设计部， 北京 100094； 2.中机生产力促进中心， 北京100044）

0 引言

对于高精度测绘卫星来说，各测量载荷之间需要配合使用，并保持相对位置稳定。因此除测量载荷本身的精度外， 航天器结构尺寸稳定性对测量数据精度的影响也越来越不可忽略。目前，在国内外高精度和科学探测卫星中广泛应用的较为成熟的航天器结构热变形分析技术是基于在轨仿真分析温度场计算热变形。 游思梁等通过直接计算得到的温度场计算得到天线在轨热变形[1]；Stephen 等在针对LISA 卫星开展的光机热建模与分析中通过I-IDEAS 软件仿真得到热变形分析的温度场[2]；刘振宇等利用I-IDEAS 软件分析得到的在轨温度场完成了对空间太阳翼的变工况在轨热变形分析[3]；潘腾、张也驰等利用普通克里格法对温度实测点进行插值并以此计算了载荷结构热变形[4]；帅永等采用自适应算法和加权算法求解航天器热平衡试验中多热源非线性温度场反演问题[5]；罗文波等建立了一种基于模型和在轨测量数据的温度场反演方法，并以此分析了结构稳定性指标[6]。 但是目前方法均利用完整温度场对航天器热变形进行计算，计算量大、资源需求多。 工程需求的航天器在轨热变形分析一方面仅关注关键部位的变形情况； 另一方面卫星上可利用的资源和可测量的数据十分有限。 因此，由部分已知信息获取关键部位的变形情况具有重要的工程应用价值。 本文利用航天器上有限个测量点的温度测量数据， 通过长短期记忆网络 （Long Short-Term Memory，LSTM）对其热变形进行预测，并对结果进行了分析。

1 热变形预测方法

1.1 总体思路

本文采用神经网络的方法， 通过有限个测量点的温度测量数据对航天器结构热变形进行预测。 首先选取有限个航天器有限元模型节点的温度数据与变形数据作为神经网络训练的样本集； 然后采用贝叶斯优化算法对神经网络超参数进行优化； 最后对比选择优化后的神经网络用作航天器热变形预测。 具体流程如图1 所示。

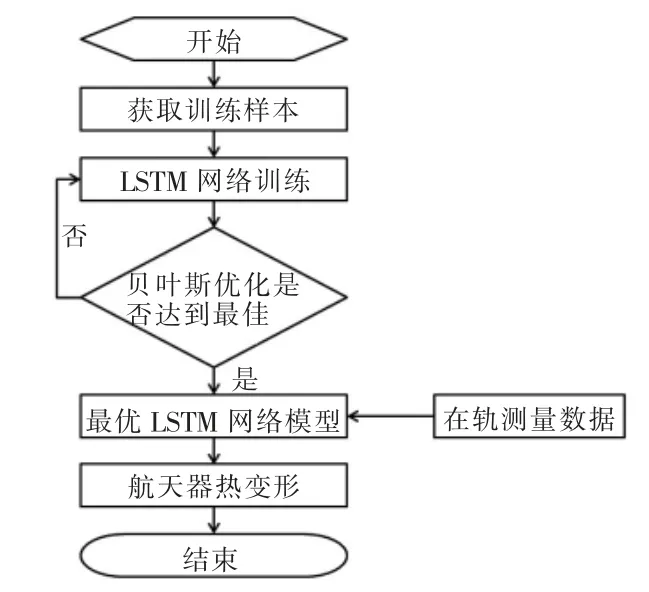
图1 热变形预测方法流程

1.2 数据选取与处理

高分七号是我国首颗亚微米级高分辨率光学传输型立体测绘卫星， 配置双线阵相机和2 束激光测高仪， 能获取高空间分辨率立体测绘遥感数据和高精度激光测高数据。本文采用文献[6]中方法，基于在轨温度测量数据反演出卫星结构在轨温度场。 输入数据为高分七号有限元模型节点温度，在本文中作为精确值；输出数据为高分七号两个相机与激光测高仪安装面拟合平面法线矢量之间的夹角，该夹角通过在有限元模型上施加完整温度场计算而得，变形计算采用的有限元模型根据地面热变形试验已完成模型修正， 在本文中作为精确值。用于神经网络训练的样本集记为：式中：xi—输入数据，组成输入空间X；yi—输出数据，组成输出空间Y。

为了使用较少的作为输入数据的节点， 即降低输入数据维度，需要对卫星有限元模型节点进行选择。高分七号完整有限元模型如图2 所示， 其中载荷模型及其安装结构认为是恒温，需人工筛去，只保留部分结构模型，如图3 所示。然后识别出与输入数据相关性高的节点，本文采 用 最 大 信 息 系 数[7]（Maximal Information Coefficient，MIC）作为相关性度量。

直接作为本文输出数据的是卫星载荷安装面法线矢量间的夹角， 需要对有限元方法计算得到的安装节点位移进行转化，转换方法为文献[8]中提出的点云数据平面拟合方法。 卫星三个载荷安装面法线矢量之间的夹角分别定义为O1、O2、O3。

为了消除数据数量级对神经网络训练精度的影响，需要对数据进行归一化。 设原始输入数据为：

同理，输出数据也在对原始数据进行归一化得到，并与输入数据组成样本集D。

1.3 基于LSTM 网络模型的热变形预测

图2 高分七号完整有限元模型

图3 高分七号部分结构有限元模型

卫星于轨道空间呈周期性运动， 其热环境具有一定的周期性， 因此其温度及热变形数据是与时间相关的时间序列。 循环神经网络（Recurrent Neural Network，RNN）将时序的概念引入到网络结构的设计中， 是一类具有短期记忆能力的神经网络。 循环神经网络的参数学习可以通过随时间反向传播算法（Backpropagation Through Time，BPTT）[9]来学习。 但是当输入序列比较长时，会存在梯度消失和梯度爆炸问题[10]，即长程依赖问题。 在众多RNN 的变体中，长短期记忆（Long Short-Term Memory，LSTM）模型引入了输入门、 遗忘门和输出门的门控机制[13]， 弥补了RNN 的长程依赖问题和长期记忆能力不足等问题，使得循环神经网络能够真正有效地利用长距离的时序信息。

设一个给定的输入序列为x1：T=（x1，x2，…，xt，…，xT），则LSTM 网络前向计算公式可以表示为：

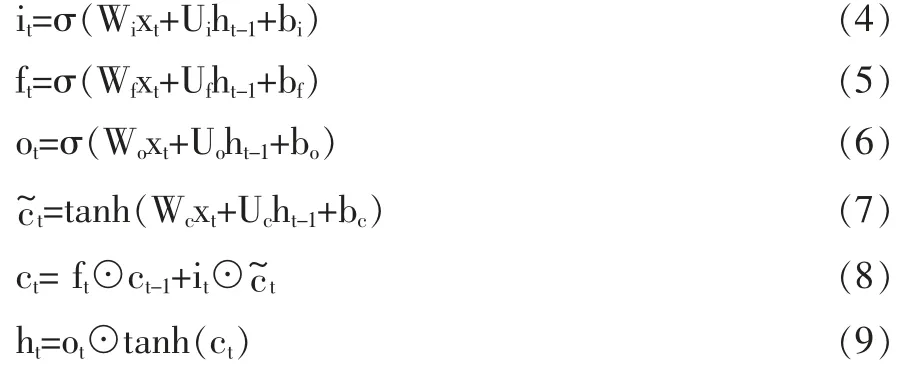
式中：ht、it、ft、ot、ct分别为t 时刻隐含层活性值、输入门、遗忘门、 输出门和细胞状态；W、U、b 为网络参数；σ 和tanh 分别为sigmoid 函数和双曲正切激活函数。

LSTM 网络参数学习采用的是与经典反向传播（Back Propagation，BP） 算法原理类似的BPTT 算法，其步骤为：①式（4）～式（9）计算LSTM 细胞的输出值；②反向计算每个LSTM 细胞的误差项； ③根据相应的误差项计算每个权重矩阵的梯度； ④应用基于梯度的优化算法更新权重矩阵。

目前， 深度神经网络的参数学习主要是通过梯度下降法来寻找一组最小化结构风险的参数， 可以分为批量梯度下降、 随机梯度下降和小批量梯度下降三种形式。 本文选用的是适应性动量估计（Adaptive moment estimation，Adam）算法[14]。 Adam 算法不但使用动量作为参数更新的方向，而且可以自适应调整学习率。 LSTM 网络模型训练过程中使用的损失函数为常用于回归问题的平方损失函数，其定义为：

式中：f（xi）为LSTM 网络模型预测值。

LSTM 网络结构包括输入层、隐含层和输出层。 本文对比两种不同隐含层的LSTM 网络模型，分别记为neta和netb，两种模型结构分别如图4、5 所示。 neta为单隐含层；netb两层LSTM 层中间加一层丢弃层。

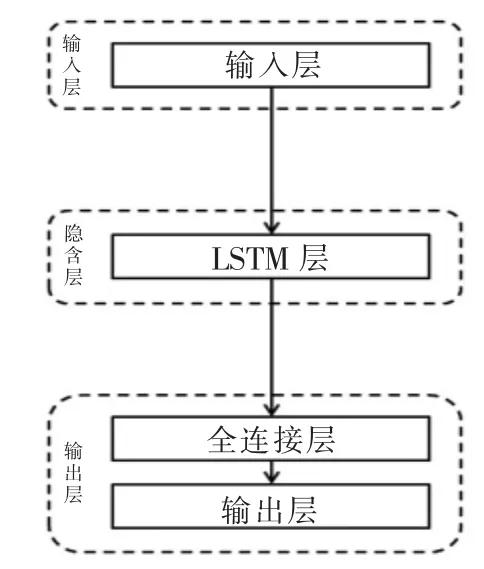
图4 LSTM 网络结构neta

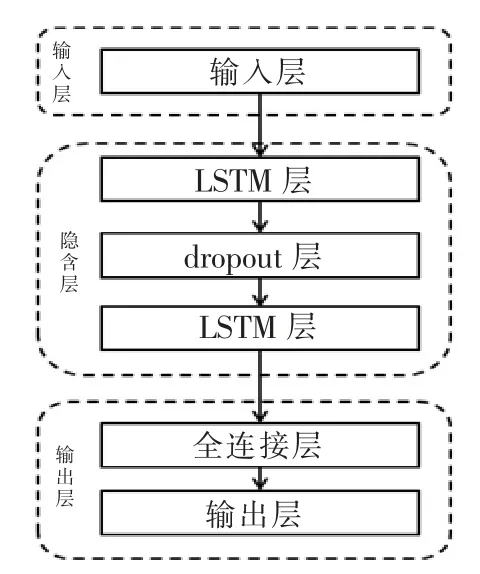
图5 LSTM 网络结构netb

LSTM 网络训练收敛判据为：①验证集最小均方误差连续6 次不更新；②训练集最小均方误差连续10 次不更新；③训练集均方误差减小幅度连续10 次小于ε，本文中令ε=10-5。 三个收敛判据满足其一，即停止网络训练并认为其收敛。

1.4 贝叶斯优化LSTM 网络模型超参数

在神经网络中，除了可学习参数外，还存在不能直接通过训练学习的超参数需优化。 常用的超参数优化方法有网格搜索、随机搜索、遗传算法、粒子群算法和贝叶斯优化等。 其中贝叶斯优化是一种以贝叶斯定理为理论基础的自适应的超参数优化算法[15-16]，其根据当前已经试验的超参数组合来预测下一个可能的最大收益组合，只需要较少次数的目标函数评估即可获得理想解，非常适用于求解目标函数未知、非凸、多峰和评价代价高的复杂优化问题[17-18]。 本文采用贝叶斯优化算法对LSTM 网络模型的超参数进行优化，待优化的变量及其约束条件如表1 所示。

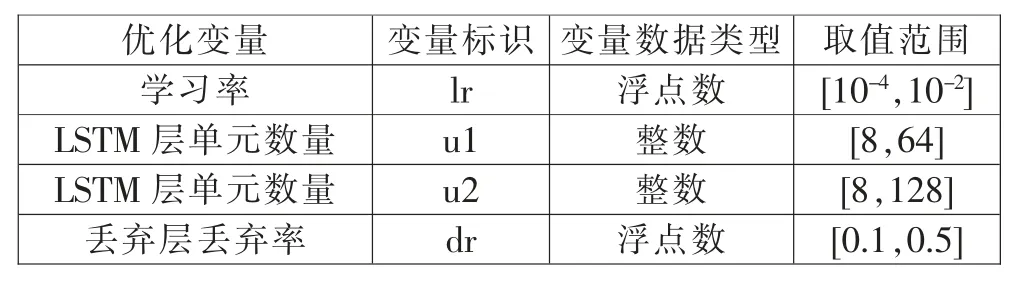
表1 待优化参数约束条件

2 度量指标

2.1 超参数优化目标函数

通过贝叶斯优化算法对LSTM 网络模型超参数进行优化， 优化过程中以测试集均方根误差 （Root Mean Square Error，RMSE）作为待优化目标函数。 RMSE 计算公式为：

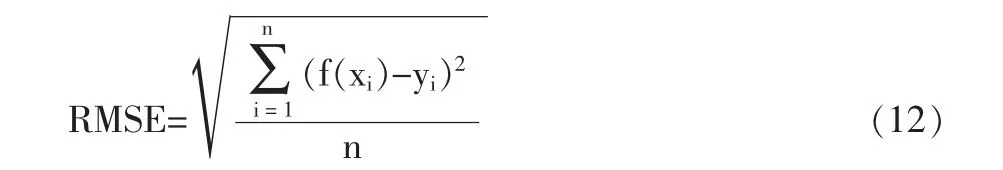
式中：f（xi）、yi分别为观测值和目标输出值，n 为样本数量。优化过程中， 满足优化次数大于50 次且15 次没有更新最小目标值的条件，即认为达到最优解。

2.2 LSTM 网络评价指标

RMSE 不仅可以作为优化超参数的目标函数， 而且可以对LSTM 网络模型的整体预测精度进行量化评价。除此之外，本文还分别选择平均绝对误差（MAE）、平均相对误差（MAPE）和最大绝对误差（MaxAE）从多角度对LSTM 网络模型进行精度量化评价，其计算公式分别如式（13）～式（15）所示。

式中：由于样本变化范围仅为其目标值10-6量级，因此在计算MAPE 时， 选取样本目标值的峰峰值P 作为计算时的分母，P= max（yi）-min（yi），i=1，2，…，n。

3 算例分析

结合高分七号温度测量在轨数据， 应用贝叶斯算法优化LSTM 网络模型并展开分析。样本原始数据来自高分七号在轨测量数据及有限元仿真分析热变形， 共20 轨，每轨包括190 个测量时刻，即共3800 组数据。将样本集D按70%、15%、15%的时序比例分为训练集、验证集和测试集，其中训练集用于LSTM 网络模型的参数学习，验证集用于防止训练过拟合，测试集用于模型预测结果检验。

3.1 实验设计

为探究不同影响因素对预测精度的影响， 设计了变量包括输入数据选取方法、输入维度、输出维度和LSTM网络结构的对照实验组，如表2 所示。其中输入数据选取方法为1.2 节中提到的MIC 方法，记mki为第i 个节点与第k 个夹角之间的MIC 值，其矩阵形式为：

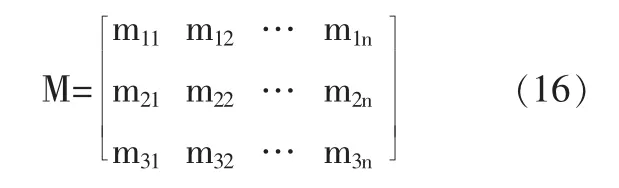
MIC 值越大，相关性越高。 本文中根据MIC 系数选取输入数据方法分为两类：一类是矩阵M 每列取均值并降序排列，按输入维度选取MIC 均值大的节点， 节点温度即为输入数据，记为方法M；另一类矩阵M 每行分别降序排列，分别选取每行MIC 系数大的节点，记为方法I。同时，由于有限元模型及温度场自身特性，相邻节点的MIC 值可能非常接近，因此从温度测点分布的角度考虑， 需要对选出的节点再进行一次相关性筛选。

为比较输出维度对预测精度影响，设置了输出维度分别为1 和3 的对照组， 相应需要训练的LSTM 网络模型数量分别为3 和1。

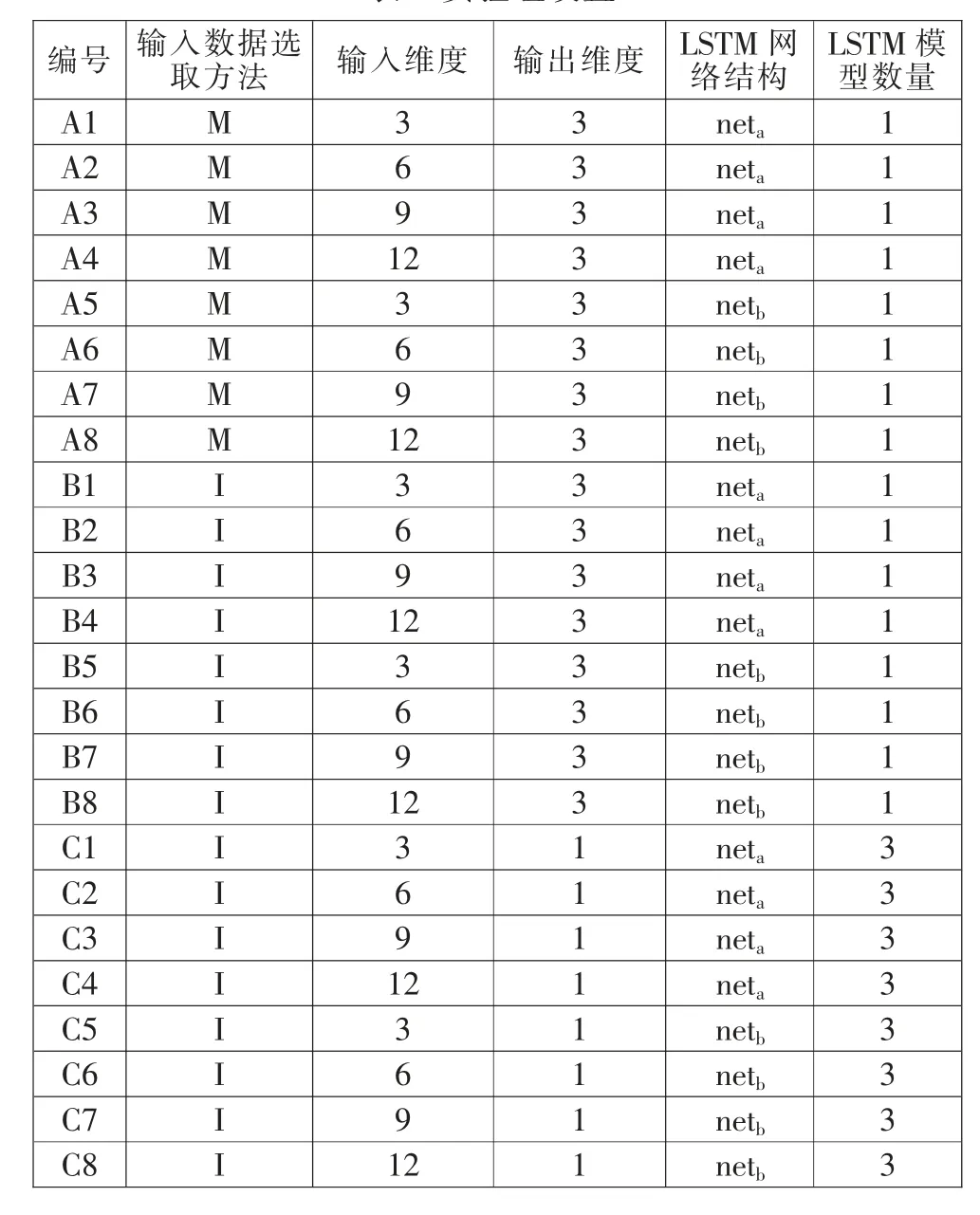
表2 实验组设置

3.2 结果分析

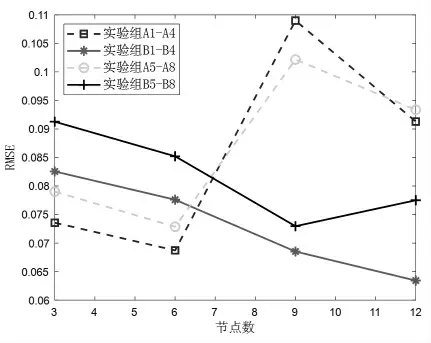
图6 实验组A1-A8 及B1-B8 贝叶斯优化结果

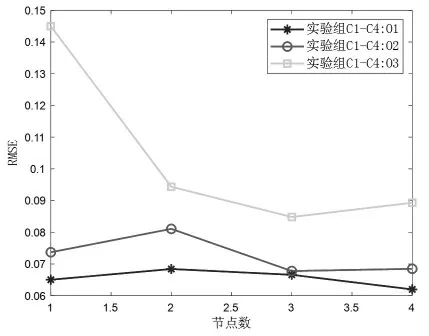
图7 实验组C1-C4 贝叶斯优化结果

贝叶斯优化算法对LSTM 网络模型超参数优化结果如图6-图8 所示。 图中所示横坐标为选取作为输入数据的节点数量，即输入维度；纵坐标为测试集RMSE，其值越小表示对测试集整体的预测精度越高。 根据结果进行分析可以得出如下结论：①整体上来说，RMSE 随输入维度增加呈下降趋势，其中实验组B4 输入维度为12，预测精度最高，RMSE值为0.0634。实验组B4 的LSTM 网络模型测试集预测结果与目标值对比情况， 见图9； ②对比输入数据选取方法M 和I， 方法M 在输入维度为3 和6 时，预测效果优于方法I； 但当输入维度较大， 即为9 和12时，方法I 预测效果优于方法M；③输入维度对多层结构网络netb预测精度的影响小于单层结构网络neta， 这与netb具有更好的泛化能力有关； ④实验组C1-C4 和C5-C8 整体随输入维度增加变化趋势相似， 其中对输出O3的预测精度随输入维度增加而更高的趋势最大， 变化幅值分别为0.0602 和0.1055， 这与卫星自身热变形有关，即沿某一方向变化较明显，其余两个方向变化较弱。

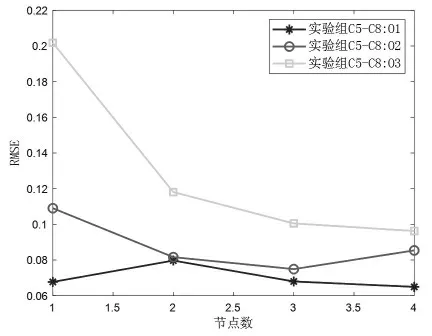
图8 实验组C5-C8 贝叶斯优化结果

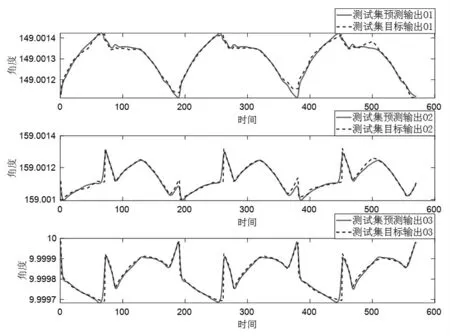
图9 实验组B4 贝叶斯优化结果

各实验组LSTM 网络模型测试集预测结果的MAE、MAPE 和MaxAE 如表3 所示。MAE 和MAPE 最小值均为实验组C2 和C3， 其中MAE 最小值分别为7.956×10-6、8.609×10-6和7.177×10-6，MAPE 最小值分别为2.60%、2.63%和2.45%，但两个实验组都出现对某一维度预测效果较差的现象，这与C 实验组采用三个独立的LSTM 网络模型分别对三个维度输出进行预测有关，即对三个维度输出的预测各自独立； 实验组A6 虽然对三维输出的预测效果在对比实验组中不是最小值，但是对三维输出整体预测效果较好。 MAPE 给出了LSTM 网络模型预测的最大绝对误差，其工程意义在于一定程度上给出了误差变化范围。

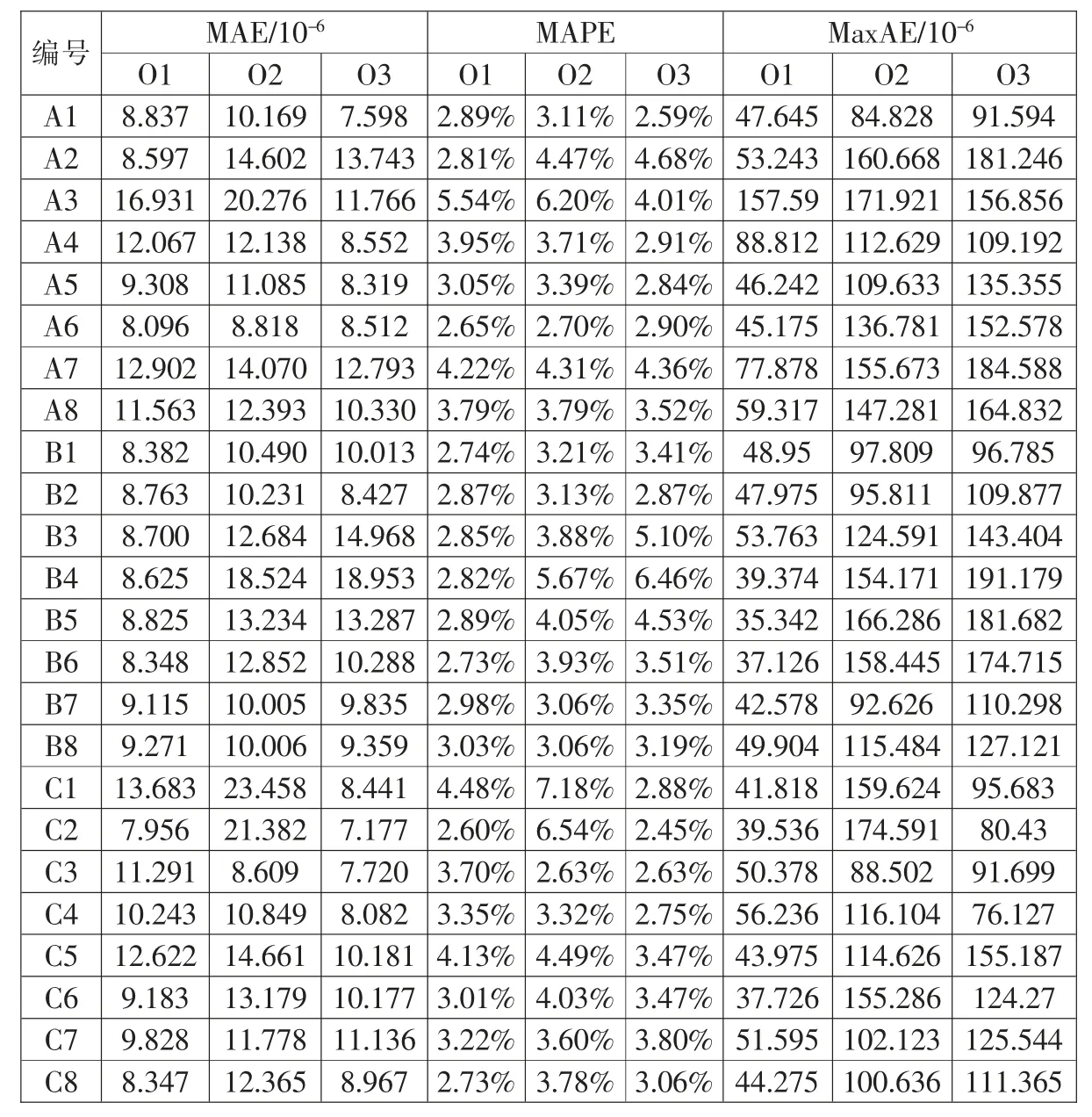
表3 LSTM 网络模型预测MAE、MAPE 和MaxAE

4 结论

本文针对高精度测绘卫星结构尺寸稳定性问题，提出了基于较少在轨温度测点和LSTM 网络模型的航天器热变形预测方法， 包括训练数据选取与处理、LSTM 网络模型预测以及超参数优化等内容。 原始在轨测量数据经过选取和预处理，提高了计算精度。设计了包含多个对照实验组的LSTM 网络模型预测实验。 采用贝叶斯优化算法对LSTM 网络模型超参数进行优化， 得到超参数的最优解。 实验验证表明：①单层结构LSTM 网络模型与多层结构相比， 单层结构网络对航天器热变形问题预测更准确，但是其受输入维度影响更大，预测精度随输入维度增大而更高；②输入数据选取方法根据不同维度输出分别选取，以达到更高的预测精度；③对不同维度输出分别做各自独立的LSTM 网络模型训练可以达到更高的精度，但资源占用更多。

本文探索了LSTM 网络模型在航天器热变形预测领域中的适用性，扩展了深度学习技术的应用范畴；分析了该方法在航天器热变形预测问题中的结果，验证了该方法的有效性。