基于二进制粒子群算法的母联闭合型电网重构策略

梁浩哲， 龚喜文

(上海船舶运输科学研究所 航运技术与安全国家重点实验室，上海 200135)

0 引 言

在设计海工平台中压电力系统时，通常要求其在保证用电经济性和灵活配置的同时，能在复杂条件下安全可靠运行。然而，海工平台电力系统在恶劣海况、人为操作失误和设计存在隐患等情况下都有可能发生故障，轻则降低系统的可信任度，重则引起设备损毁和供电通路阻滞[1-3]。因此，对电力系统在发生故障情况下的快速恢复策略进行研究具有重要意义。

1 母联闭合型电网故障恢复模型

深水半潜平台电力系统在DP-ER(Dynamic Positioning System with Enhanced Reliability)模式下工作时，各电站之间采用环形方式连接。当电网发生故障时，采取故障恢复策略的实质是对电力系统进行重新配置，构建一个新的供电网络[4],具体如下：

1)获取电网中各节点的开关状态信息；

2)通过控制备用供电支路供电开关的通断，隔离故障负载；

3)在满足负载容量、供电开关通断次数和发电机组效率均衡等约束条件的情况下，实现对重要负载的快速恢复供电。

1.1 母联闭合型电网结构

母联闭合型电网最早由挪威船级社提出，在DP-ER模式下，各电站之间采用环形方式连接，发电机连接主汇流板，在主汇流排下以辐射状连接负载，重要负载与次要负载相互分开连接[5]。母联闭合型电网结构见图1。

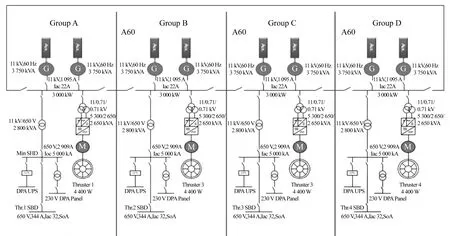
图1 母联闭合型电网结构

在该电网结构中，G1～G8是8台连接母联闭合型电网汇流排的发电机组，每台发电机组都能为所有负载线路供电。

1.2 目标函数

由于负载容量恢复值、供电支路开关通断次数和发电机效率平衡均为母联闭合型电网故障恢复效果的重要判定指标，因此本文所述模型采用这3种指标综合形成的故障恢复满意度作为目标函数，根据不同指标的重要程度设置不同的权值。

1)目标一：恢复负荷容量。

船舶电力系统通常根据承载的电路的不同分为3个级别，其中属于重要负载的船舶电力系统为一级和二级，有2条配电路线，分别为正常供电路线和备用供电路线[6]。考虑以故障发生后最大程度地恢复重要负荷的容量为目标，对不同负荷的重要程度进行划分，得到恢复负荷容量的目标函数为

(1)

式(1)中：Lg1为一级负载容量；Lg2为二级负载容量；Lg3为三级负载容量；xi、xj和xm取值为0或1，其中,1表示负载供电，0表示卸载；α、β和γ分别为一级负载、二级负载和三级负载的权重系数，可根据不同负载的重要性对其权重进行设定，本文所述模型定义α=1，β=0.1，γ=0.01；N1、N2和N3分别为一级负载、二级负载和三级负载的数量。

2)目标二：负荷供电支路开关通断次数。

系统故障恢复是指通过控制开关，找到最快、最合适的重构供电路线。开关通断次数的目标函数为

(2)

式(2)中：S1i、S2j和S3k分别为一级负载、二级负载和三级负载开关。

3)目标三：发电机效率均衡。

在重构电力系统网络时，要考虑发电机的工作效率，防止某台发电机的工作效率突然变得过低。因此，将发电机效率均衡作为目标函数之一，可表示为

(3)

式(3)中：PGi为发电机实际功率；PGm为发电机额定功率。

根据上述3个目标重要性的不同，对这3个目标设定不同的权值，进行归一化处理之后，可得故障恢复满意度(即目标函数)的表达式为

(4)

式(4)中：Fi max和Fi min分别为将第i(i=1,2,3)个目标作为独立的目标函数优化时，可得到的目标函数最大值和最小值；wi为第i个目标的权重。wi满足关系式

w1+w2+w3=1

(5)

本文选取w1=0.7，w2=0.2，w3=0.1，在修改w1、w2和w3的数值时，需视实际情况进行修改。

对于目标一，故障发生之后，系统期望能最大程度地恢复重要负荷的容量。因此，针对某种具体的配电网故障情况，在单独考虑目标一的情况下，可计算得到重要负载的最大恢复容量，而系统中重要负载最小恢复容量的情况为没有进行故障恢复，即最小值为0。

对于目标二和目标三，系统期望依靠最少的开关通断次数和最均衡的发电机效率得到最优解，优化结果期望其越小越好。因此，在单独考虑目标二或目标三时，能优化得到最小值，但最大值并不是优化得到的，开关通断次数最大值取为系统所有的开关数量。

1.3 约束条件

1.3.1 电力系统网络结构约束

对于拥有正常和备用2条供电路线的一级负载和二级负载，在同一时间点只能导通1条供电路线[7]。系统的连续性约束和辐射状限制为

(6)

式(6)中：δi为转换开关集合；zk和zl分别为同一负载在正常和备用2种状态下的开合状态，用 0、1变量表示。

1.3.2 系统容量限制

在重构过程中，要限制系统中支路的容量，不能造成支路容量过载[8]。

(7)

式(7)中：xij为负载i和支路j的开关状态，xij=0表示开关断开，xij=1表示开关闭合；si为负荷或支路用电量；Mj为支路j的容量限制值。

2 策略实现与求解流程

在母联闭合型电网故障恢复模型中，控制变量包括负载容量和支路开关的状态。若在求解该模型过程中同时优化这2个控制变量，会面临开关状态与供电容量不匹配的问题，大大降低求解效率。实际上在求解该模型过程中，供电负荷优化要在开关状态给定的情况下进行，因此本文将求解流程分为2个阶段，其中：第一阶段采用二进制粒子群算法优化各类开关状态变量；第二阶段在第一阶段的基础上,采用粒子群算法优化供电负荷。

2.1 第一阶段

母联闭合型电网故障恢复模型中的开关通断次数为离散变量，因此第一阶段可采用二进制粒子群算法对该离散变量进行求解。二进制粒子群算法的速度更新公式为

vi,t+1=vi,t+c1r1,t(pi,t-Xi,t)+c2r2,t(Pg,t-Xi,t)

(8)

式(8)中：vi,t=(v1,t,v2,t,…,vNp,t)为粒子i第t代的速度，其中Np为种群的粒子总数；Xi,t=(x1,t,x2,t,…,xNp,t)为粒子i第t代的位置；pi,t为第i个粒子迭代到第t代时计算所得个体极值；Pg,t为整个种群迭代到第t代时计算所得全局极值；c1和c2为学习因子；r1,t和r2,t为均匀分布于[0,1]范围内的随机数。

相比粒子群算法，二进制粒子群算法的改进之处在于通过给粒子的位置值设定一个阈值进行选择，超过阈值就设为1，否则设为0，该阈值采用sigmoid函数设定。因此，保持速度公式不变，重新定义粒子的位置公式，粒子位置更新公式为

(9)

式(9)中：Ui,d,t为第i个粒子第d维迭代到第t代时的位置；r为生成的随机数，位于[0,1]区间内；vi,d,t为第i个粒子第d维迭代到第t代时计算得到的速度。sigmoid函数的表达式为

(10)

第一阶段采用二进制粒子群算法的求解流程如下：

1)输入母联闭合型配电网的系统网架结构、故障点位置和节点负荷水平等数据。

2)对二进制粒子群算法进行初始化，初始化内容包括种群规模、最大迭代次数、学习因子和权重等。

3)调用第二阶段算法，计算得到发电机功率均衡率、供电负荷恢复情况和开关状态变化次数，根据相关计算结果求取此次优化结果的综合满意度。

4)根据式(8)～式(10)更新二进制粒子的速度、位置、pi,t和Pg,t等参数。

5)根据计算得到的全局最优解判断该最优解是否收敛。若收敛，则结束求解，同时给出相应的故障恢复方案；若不收敛，则返回流程3)，重新进行计算。

2.2 第二阶段

母联闭合型电网故障恢复模型中的负荷容量为连续变量，因此第二阶段可采用粒子群算法进行计算优化。普通粒子群算法的速度更新公式与式(8)相同，位置更新公式为

Xi,t+1=Xi,t+vi,t+1

(11)

第二阶段采用粒子群算法的求解流程如下：

1)输入故障恢复之后的系统网架结构、节点负荷水平和支路阻抗等数据。

2)对粒子群算法进行初始化，初始化内容包括种群规模、最大迭代次数、学习因子和权重。

3)对母联闭合型电网进行计算，得到发电机功率均衡率和供电负荷容量，并据此计算得到综合满意度指标。

4)根据式(8)和式(11)更新粒子的速度、位置、pi,t和Pg,t等参数。

5)根据计算得到的全局最优解判断结果是否收敛。若收敛，则结束求解，同时将计算得到的供电负荷恢复容量数据反馈给第一阶段算法；若不收敛，则重新进行计算。

2.3 粒子群的离散化处理

对于本文所述电网模型而言，为将算法应用到电网故障恢复中，需对连续的变量进行离散化处理[9-10]。根据式(11)得出对应的连续值，根据负载是否有备用供电线路和划分的区间，将连续的数值对应为不同的离散值。

1)有正常供电线路且有备用供电线路：(-∞,0.5)→0,[0.5,1.5]→1,(1.5,+∞)→2。

2)有正常供电线路但无备用供电线路：(-∞,0.25)→0,(0.25,+∞)→1。

在进行离散化处理时，将连续值转换为离散值，离散值代表开关的切换，并将相应的切换动作转换为负载供电状态：离散值为0，代表负载处于失电状态；离散值为1，代表负载处于正常供电状态；离散值为2，代表负载处于备用供电状态。

3 算例分析及对比

3.1 算例设置

根据母联闭合型电网的系统架构图对其网络进行分解、抽象之后，可得到其电力系统网络拓扑结构。母联闭合型电网拓扑图见图2,其中:G1～G8为8台连接主配电板的发电机组；L1～L20为网络中的供电负载；1～52为52条供电支路。平台电力系统中各负载的容量和相应等级见表1。

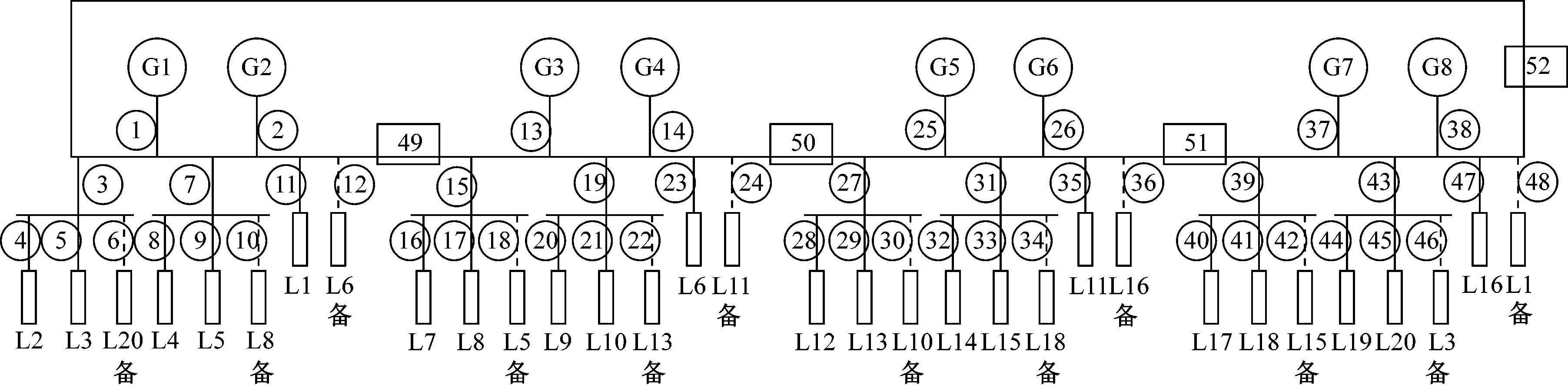
图2 母联闭合型电网拓扑图

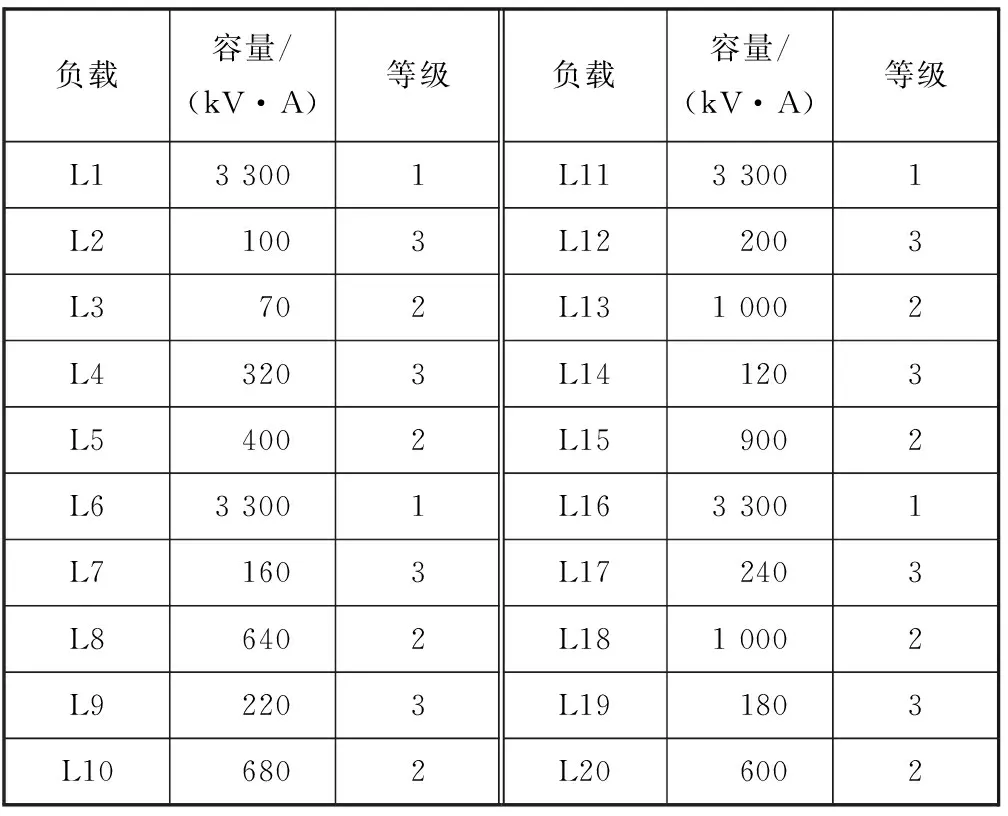
表1 平台电力系统中各负载的容量和相应等级

本文所述算例设定支路13、支路31、支路49和支路50等4条供电线路发生故障，模拟故障导致的孤岛运行情况。采用MATLAB语言编写故障恢复算法，对设置的故障情形进行模拟仿真;为对比采用不同算法得到的优化结果，输入相同的仿真参数，对该算法与混沌遗传算法和免疫克隆选择算法进行模拟仿真对比。

初始化参数设置：种群规模Np=100；最大迭代次数Tmax=100；学习因子c1=c2=2；权重系数α=1,β=0.1,γ=0.01。

3.2 算例仿真对比

根据本文建立的母联闭合型电力系统故障恢复模型，采用二进制粒子群算法、混沌遗传算法和免疫克隆算法对上述模型进行故障恢复仿真，3种算法的最优个体适应度变化情况见图3，故障恢复结果比较见表2。

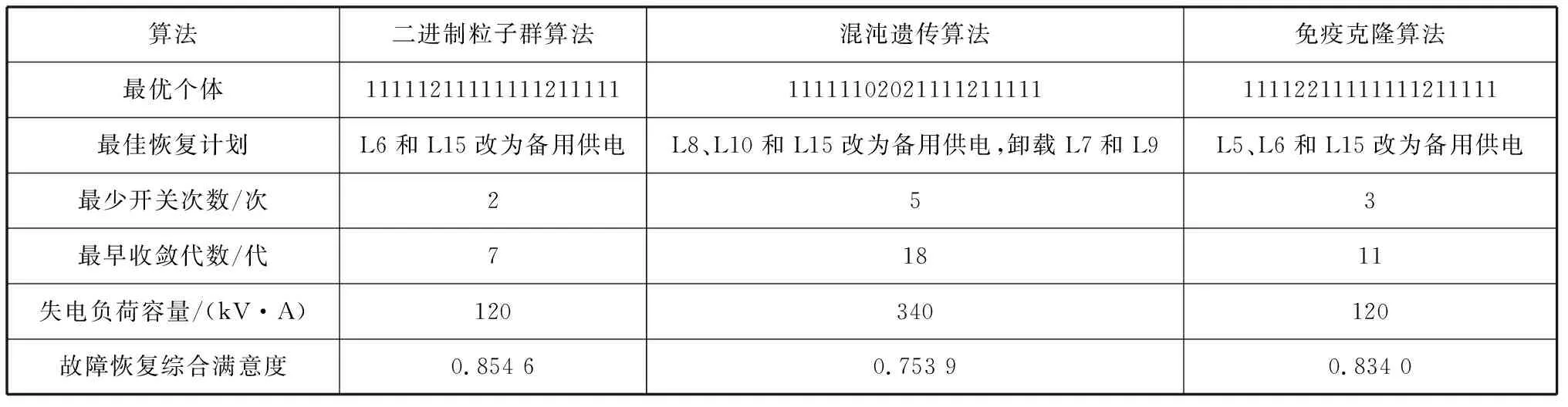
表2 3种算法的故障恢复结果比较

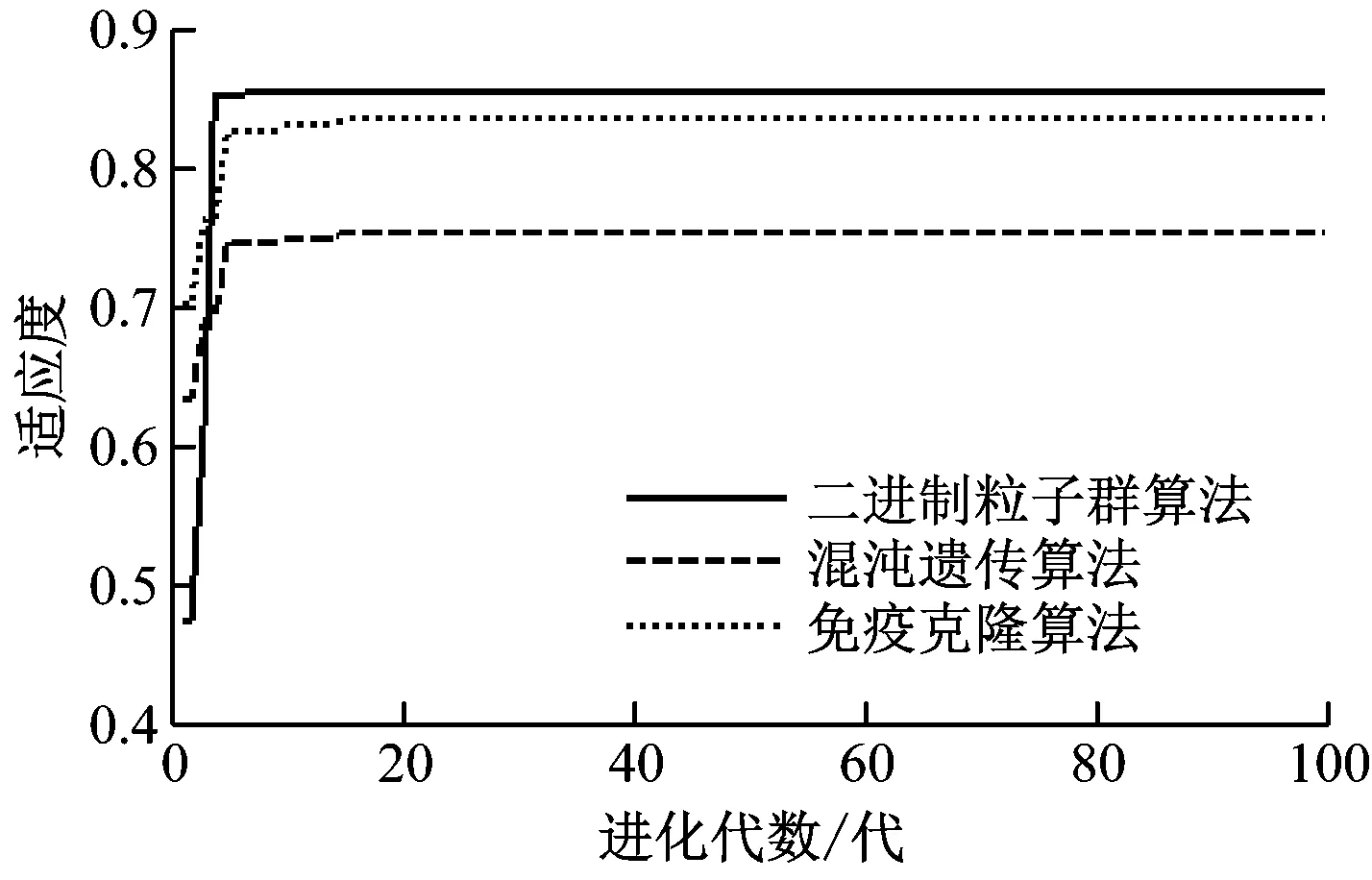
图3 3种算法的最优个体适应度变化情况

由图3可知：3种算法均可收敛，其中:两段式二进制粒子群算法和免疫克隆算法最终收敛结果的适应度较高;混沌遗传算法最终收敛结果的适应度相对较低。两段式二进制粒子群算法、混沌遗传算法和免疫克隆算法最终的适应度分别为0.854 6、0.753 9和0.834 0，收敛到各自的最优解的迭代次数分别为7次、18次和11次。通过比较可知，二进制粒子群算法相比另外2种算法迭代次数最少，收敛速度最快。

由表2可知：

1)二进制粒子群算法在第7代就找到了最佳适应度值，并趋于稳定，最优个体为11111211111111211111，最少开关次数为2次，其恢复计划为负载L6和负载L15改为备用供电。由拓扑图和负载等级表可知，负载L6为一级负载，重要程度最高，故障发生之后出现了孤岛情况，此时孤岛负载的容量已超出单台发电机的容量，因此将负载L6投切为共线母排供电是一种较好的恢复方案，而此时31支路发生故障导致负载L14和负载L15失电，负载L15改为备用供电，负载L14没有备用供电，被迫失电。该策略的故障恢复综合满意度为0.854 6。

2)混沌遗传算法在第18代找到了最佳适应度值，并趋于稳定，最优个体为11111102021111211111，最少开关次数为5次，其恢复计划为将负载L8、负载L10和负载L15改为备用供电，将负载L7和负载L9卸载。负载L6为一级负载，重要程度最高，该策略在出现孤岛情况之后保留了负载L6，将孤岛内的二级负载L8和负载L10改为了备用供电，负载L9因容量限制而被迫失电，负载L14因支路31发生故障而被迫失电。该策略的故障恢复综合满意度为0.753 9。

3)免疫克隆算法在第11代找到了最佳适应度值，并趋于稳定，最优个体为11112211111111211111，最少开关次数为3次，其恢复计划为将负载L5、负载L6和负载L15改为备用供电，该方案类似于二进制粒子群算法的策略，考虑到发电机功率平衡，增加了将负载L5改为备用供电的计划。该方案也具有较好的优化结果，但限于最少开关次数目标的权重高于发电机功率平衡目标的权重，该策略最后的故障恢复综合满意度略低于二进制粒子群算法故障重构策略的故障恢复综合满意度，其值为0.834 0。

通过以上对比可知，二进制粒子群算法的仿真结果具有最高的故障恢复综合满意度，该算法不仅收敛速度较快，而且从最后的故障恢复效果来看，具有最少的开关次数和最低的负载失电容量。因此，针对母联闭合型电网故障恢复，二进制粒子群算法具有很大优越性。

4 结 语

本文针对深水半潜平台母联闭合型电网的故障恢复问题，建立了母联闭合型配电网的故障恢复模型，提出了基于二进制粒子群算法的故障重构策略，通过二进制粒子群算法的两阶段优化求解流程，降低了多目标优化过程的求解难度，提高了算法的求解效率，提升了算法的寻优能力和收敛精度，保障了系统故障恢复的稳定性和快速性。通过算例仿真，对基于二进制粒子群算法、混沌遗传算法和免疫克隆算法的3种故障重构策略的仿真结果进行了对比，结果表明，本文提出的基于二进制粒子群算法的故障重构策略在收敛的快速性和故障恢复方案的综合满意度方面具有明显的优越性，可快速、稳定地提供一个较好的恢复方案。