冬季长江下游地区气温低频振荡和低温天气的延伸期预报研究

杨秋明 2

1 南京气象科技创新研究院，南京 210009

2 江苏省气象科学研究所，南京 210009

1 引言

冬季受东亚季风区各种不同时间尺度大尺度低频环流[主要是欧亚/太平洋型（EUP）低频流型等]的影响，位于我国东部沿海的长江下游地区（30.5°～32.0°N, 118.0°～122.5°E）的很多城市经常出现异常低温、雨雪和冰冻天气，持续时间长，严重影响经济、交通、电力、通讯和人们的正常生活。因此，详细分析冬季长江下游地区气温低频变化特征，研究该区域低温事件的10～30 d 延伸期预报，对于决策部门提前组织部署气象灾害防御，真正实现对完整天气事件的决策服务，高效有序应对气象灾害，明显降低雨雪冰冻等极端天气气候事件带来的损失具有很重要的意义。同时也为推进现代天气气候业务的发展提供有力的支撑，较好地适应互联网+、大数据和智能化的科技型现代气象业务发展新格局。

由于冬季东亚季风区大尺度低频环流型和温度型异常频繁活动，容易导致长江下游地区出现雨雪、强寒潮和低温冰冻灾害。每年欧亚中高纬度和低纬度环流的相互作用都有部分相同的特点，但更重要的是气候背景场与大尺度低频扰动之间的各种相互作用机制差异的复杂性[如对流层中的低频Rossby波的传播及高频瞬变涡动的反馈强迫作用（Bueh et al., 2011）、扰动的形态与急流位置之间的配置关系变化（Zeng, 1983）、冬季北半球各阻塞系统对大范围温度异常和极端低温事件的单独和协同影响（李亚飞和任荣彩, 2019）等]，导致这些热带外地区环流系统的突变与低频波列传播的多样性。所以，建立能够精确描述东亚地区冬季风系统主要成员活动与变化的“普适性”的动力学模型比较困难。由于气候数值预测的数学、物理基础理论尚不完善，较长时效的10～30 d 延伸期变化的动力预测误差较显著，数值模式的预报时效和性能目前仍不能满足延伸期业务的需求。但是，大量气象观测数据包含全局特有的多种宏观信息，我们可以间接地对宏观现象（如不同时间尺度的两半球热带或热带外地区大尺度低频流型的变化等）进行分析、建模和计算，实现有关知识的合成和预测（杨秋明,2015, 2018）。同时通过改进数据分析方法，可以提高从实时数据中提取这些大尺度低频信号的精度。因此，充分利用长序列气象数据资源，进一步识别各种时间尺度的大气低频信息，更精确地提取实时低频信号，明显减小初始时间滤波值的误差，分析低频信号强度的时间变化，由数据驱动构建各种更好的简化数据模型进行10～30 d 延伸期预报，是显著延长预报时效的重要途径之一。

10～30 d 延伸期尺度是天气尺度和气候尺度的衔接部分，因此延伸期过程问题既有初值问题也有外强迫问题，这正是延伸期预报方法研究的难点（丑纪范等, 2010; Hoskins, 2013）。不同于天气预报和短期气候预测，延伸期预测能力完全依赖于大气低频变化规律。1990 年以来，国内外很多气象学者从不同的角度对延伸期预报方法进行了大量研究（丁一汇和梁萍, 2010; 何金海等, 2013; Kondrashov et al, 2013; 杨 秋 明, 2015, 2016, 2018; Zhu and Li,2017a, 2017b, 2018; Sabeerali et al., 2017;Krishnamurthy, 2018; 章大全等, 2019），主要有集合数值模式（Vitart and Molteni, 2010; 郑志海等,2012; 韩世茹等, 2019）、动力—统计（陈官军等,2017; Sahai et al., 2017; Abhilash et al., 2018;Karpechko, 2018; Lavaysse et al., 2019）、 统 计（Xia et al, 2015; Székely et al., 2016; Wang et al.,2016; Zhu and Li, 2017a, 2017b, 2018; Sabeerali et al., 2017; Stan and Krishnamurthy, 2019）、大数据（杨秋明, 2015）等方法，其中，采用集合数值模式（Neena et al., 2014）或数据驱动的简化随机动力模式（Kondrashov et al., 2013; Chen et al., 2014;Chen and Majda, 2015）预测方法，热带大气30～60 d 振荡（谢义炳等, 1963）[国外学者称之为MJO（Madden and Julian, 1971）]的预测时效已逐步延长到12～25 d（Neena et al., 2014），ECMWF模式达到36 d（Lim et al., 2018），北半球夏季热带季节内振荡（Boreal summer intraseasonal oscillation,BSISO）（Lee et al., 2015）的预测时效也达到了20～25 d 左右。近年来，采用观测数据中的30～60 d 低频分量和历史信息，热带对流和强降水、中纬度地区低频环流、热带气旋活动和移动的预报技巧延长到3～4 周。与夏季区域强降水、高温和冬季低温过程密切联系的中国降水和气温10～80 d低频分量的延伸期预报时效已达5～6 候左右（Zhu and Li, 2017a, 2017b, 2018），但10～30 d 低 频 分量的预测时效仍小于3 候。关于长江下游地区夏季延伸期预报方法，近10 年来国内外的研究主要集中于多种时间尺度（10～20 d、20～30 d、30～50 d 和50～80 d 等）的季节内振荡（Intraseasonal Oscillation, ISO）的低频降水和暴雨（强降水）过程预测，采用动力、统计、大数据等多种方法（杨秋明, 2015），取得了很多有意义的成果，低频降水预报时效达到25～30 d 左右（Yang, 2018），特别是对于20～30 d 振荡（杨秋明, 2009）较强的年份，已延长到50 d 左右（杨秋明, 2014a）。另外，与夏季长江下游高温有密切联系的长江下游30～60 d 低频温度的预报时效达23 d 左右（杨秋明,2018）(http://www.lcjrerf30.org [2020-05-20])。但是，用长序列数据详细分析冬季长江下游地区极端低温天气和ISO 变化的联系和最相关的周期对应的低频振荡的研究仍然不多，用这些关键周期对应的低频分量构建预测模型进行延伸期预测的试验较少。此外，过去的很多延伸期预测方法研究中，采用经典的滤波方法[如，Butterworth 滤波（Murakami,1979）、小波分析（Torrence and Compo, 1998）、经验模态分析（Empirical mode decomposition, EMD）（Love et al., 2008）、奇异谱分析（singular spectrum analysis, SSA）（Ghil and Kingtse, 1991; Mo, 2001）等]，其右边界附近20～50 d 滤波值误差较大，或提取的ISO 信号明显偏弱。这种较大误差的实时滤波初始值会导致各种基于低频分量的延伸期预测模型的预报不稳定，明显缩短预报时效。因此，采用合适的数据分析和变换方法，抑制经典滤波方法的边界效应，更精确地从实时数据中提取低频信号，是需要研究的另一个主要问题。

本文将基于逐日长序列（1979 年1 月1 日至2018 年12 月31 日，14610 d）观测数据，分析各种次季节时间尺度的长江下游气温低频振荡和12～2 月低温日数的关系，研究长江下游地区气温主要低频分量和东亚850 hPa 温度的低频主成分之间的联系和时间变化特征，揭示与长江下游地区冬季低温过程最相关频段对应的关键周期；用奇异谱分析（SSA），得到长江下游气温和东亚850 hPa 温度的主要低频分量；并由动态数据来驱动各种复杂低频变化过程与系统的构建，建立扩展复自回归模型（Extended complex autoregressive model, ECAR）（杨秋明, 2014b; Yang, 2018）[低频分量预测模型LFCF2.0（杨秋明, 2015）]，对2001/2002～2017/2018 年12～2 月逐日长江下游地区的主要温度低频分量进行实时的独立延伸期预测试验。在预测试验中，采用实时SSA 滤波方法（Yang, 2018）提取低频分量，显著减弱经典SSA 滤波的边界效应，同时也讨论了冬季长江下游低频温度可预报性的年际变化。

2 数据和方法

长 江 下 游 地 区（ 30.5°～32.0°N, 118.0°～122.5°E）逐日气温采用1979 年1 月1 日至2018 年12 月31 日（共14610 d）期间的25 站平均值，东亚地区850 hPa 温度场选用同期NCEP/NCAR 逐日格点再分析资料（2.5°×2.5°），低频温度分量的独立预报试验时间是2001/2002～2017/2018 年每年12 月1 日至次年2 月28 日（共1530 d）。本文参 照ETCCDMI（Expert team on climate change detection, monitoring and indices）定义极端气候事件指数的方法（Alexander et al., 2006），通过温度百分位法定义极端低温日：对于长江下游地区，每年冬季（前一年12 月1 日至当年2 月28 日，1979 年至2018 年共39 个冬季）逐日的日平均温度距平的第10 个百分位的值（按由小到大的排列顺序）的平均作为定义低温日的阈值，将长江下游平均温度低于阈值的日期记为低温日。这样即建立起逐年冬季长江下游地区低温日数时间序列。首先，对每年12～2 月长江下游逐日气温进行非整数波功率谱分析（Schickedanz and Bowen, 1977），研究主要季节内周期振荡型及其强度的年际变化特征，分析不同时间尺度的温度ISO 强度与12～2 月长江下游地区低温日数之间的联系，并研究东亚850 hPa低频温度与长江下游主要温度低频分量的关系。然后，对长江下游逐日气温原始观测序列和由主成分分析（Principal Component Analysis, PCA），得到东亚（15°～60°N, 60°～150°E）850 hPa 温度场主要空间模态和时间系数分别应用SSA 滤波，重建长江下游气温和850 hPa 温度场各种主要的季节内振荡信号的分量序列。进一步选择这些低频分量中相关性较显著的分量序列组成扩展资料阵，建立扩展复数自回归模型（ECAR）（杨秋明, 2014b; Yang,2018）进行延伸期独立预测试验，预测温度低频分量次季节变化，并研究预报技巧的年际变化。在预测试验中，选择合适的子序列长度，滑动进行动态建模，适应经过数据变换后得到的复数低频分量之间相关的时间变化，显著提高ECAR 模型的预测稳定性。另外，本文在实时ISO 信号提取时，采用基于T-EOF 延拓的实时SSA 滤波，显著提高边界附近滤波值精度（实时滤波中只使用初始时间t0以前的数据），可以有效地抑制经典SSA 滤波的边界效应。这种全面反映原始序列信息的实时SSA 滤波方法（Yang, 2018）能较准确地提取ISO振幅和位相变化信息，十分适合于实时延伸期预测。

3 冬季长江下游地区气温季节内振荡与低温日数的关系

为了详细分析12～2 月长江下游逐日温度的ISO 型的年际变化特征，对1979/1980～2017/2018年逐年冬季12 月1 日至2 月28 日（39 个冬季）的逐日温度序列做非整数波功率谱分析，作二维的时间—周期图（图1a）。从图1a 可见，能通过0.01 显著性水平检验的主要周期为15～25 d、25～40 d、50～70 d。15～25 d 振荡除了1993/1994 年、2013/2014 年和2015/2016 年表现不显著外（其中2013/2014 年显著周期延长到26 d，2015/2016 年缩短为13 d），其余时间均显著存在，大多能通过0.01 显著性水平检验；25～40 d 的周期振荡主要明显存在于1979/1980～2017/2018 年期间的大部分冬季，但1994/1995～1995/1996 年、2006/2007～2007/2008 年振荡较弱；而50～70 d 周期在1988/1989～1990/1991 年、 1994/1995～1995/1996 年 和1999/2000～2001/2002 年期间振荡不明显，其余年份均较显著。因此，12～2 月长江下游逐日温度存在显著的多周期振荡，主要表现为15～25 d、25～40 d和50～70 d 的周期振荡，同时存在明显的年际变化。以上分析出的次季节时间尺度的长江下游冬季逐日气温各种振荡的变化，是冬季持续低温冰冻产生的基本条件之一。揭示其与长江下游地区冬季低温过程最相关频段对应的关键周期，并建立对应时间尺度的低频分量变化的模型进行预测，对于提高长江下游地区冬季低温过程的延伸期预测精度非常重要。

图1b 是1979/1980～2017/2018 年冬季12～2月长江下游地区低温日数的变化，其中1983/1984 年、1984/1985 年冬季最多（20 d），1994/1995年、2006/2007 年和2016/2017 年冬季无区域低温日数。从图1c 中可以发现长江下游地区冬季低温日数与周期为25～40 d 范围内的温度周期振荡强度均呈现一致的正相关，其中最显著的温度振荡周期是30 d，表现为极显著的正相关，相关系数是0.418（通过99%信度水平的显著性检验）。对于冬季25～40 d 左右的气温振荡增强的年份，长江下游地区低温日数明显偏多。这种25～40 d 左右的气温ISO 型的关键周期略长于夏季长江下游强降水（暴雨）过程显著相关的28 d 降水ISO 的周期（杨秋明, 2009），表明与冬季长江下游低温和夏季强降水密切相关的主要ISO 型变化特性有一定差异。由于冬季长江下游地区低温日数和气温25～40 d 低频振荡关系密切（对10 d 以上的低温天气过程预报具有更好的指示意义），本文主要针对25～40 d 时间尺度，基于上述39 个冬季的数据，构建预测模型预测冬季长江下游地区低频温度分量，为冬季长江下游地区持续低温冰冻过程的10～30 d延伸期报提供重要预报信息。

4 长江下游地区25～40 d 低频温度与东亚850 hPa 低频温度模态的联系

图1 1979/1980～2017/2018 年长江下游地区12～2 月（a）逐日气温主要周期的年际变化，（b）低温日数的年际变化以及（c）低温日数与周期为10 d、11 d、……、71 d 气温振荡强度的相关系数。图a 中横坐标表示各个周期（对应非整数波功率谱），黑色等值线表示不同周期功率谱对应的回归方程统计量变化，阴影区表示通过99%信度水平的显著性检验，图c 中红色水平虚线表示95%信度水平Fig.1 (a) Interannual variations of the main periods for the daily temperature, (b) interannual variations of low temperature days, (c) correlation coefficients between low temperature days and oscillation intensity of temperature from 10 to 71 days periods over the lower reaches of the Yangtze River (LYR) in December–February of 1979/1980–2017/2018. In Fig.a, black contours represent the variations of the statistical parameter for the regression equation corresponding to the non-integer period of power spectra (with the individual periods (non-integer) as the x-axis), shadings areas indicate periods are significant at the 99% confidence level; In Fig.c, the horizontal red dashed lines represent the 95% confidence level

欧亚和太平洋地区各环流系统之间相互作用、互为反馈，形成大尺度环流型和温度型异常活动（主要是西风带阻塞高压、西太平洋副热带高压以及东亚大槽和西伯利亚高压增强等），导致长江下游地区夏季极端降水（杨秋明等, 2012）和冬季极端低温事件的形成和异常发展，特别是各种时间尺度的冬季东亚低层大气大尺度低频温度型（伴随对应的大尺度低频环流型）的变化，是引起长江下游冬季持续低温雨雪和冰冻天气的主要原因之一。图2a（低频相关图）显示出明显的欧亚中高纬度地区经过长江下游地区向热带西太平洋地区传播的波列结构（相似于环流的EUP 低频波列），长江下游附近是最显著的正相关区（通过99%信度水平的显著性检验），同时较显著的负相关区位于欧亚大陆中纬度和西太平洋副热带地区[这些波列活动区域（主要是中国东部长江中下游及以南地区）也是方差贡献大值区（图2b）]，但热带地区不存在显著相关区（即与热带西太平洋地区25～40 d ISO 的变化的联系不显著）。它反映了冬季西太平洋副热带地区和东亚中高纬度低频系统对长江下游低频温度变化的作用，这种波列的作用也与中高纬度10～30 d 振荡的波列的作用相似（杨双艳等,2014; Yang at al., 2019）。为了详细分析东亚850 hPa 25～40 d 低频温度场的时空变化特征，经过PCA分析，得到7 个主要低频温度空间模态（由Butterworth 滤波得到东亚地区850 hPa 25～40 d低频温度场，资料时间是1979～2000 年，序列长度是8036 d），其解释方差分别是16.7%、14.6%、8.7%、7.3%、6.2%、4.5%和4.2%。进一步对1979～1997 年（19 年）和1979～1994 年（16 年）逐日东亚850 hPa 温度分别进行主成分分析，得到前7个空间模态，用不同样本长度得到的特征向量间的夹角余弦绝对值（杨秋明, 1993）考察空间分布型的时间稳定性，发现它们与上述1979～2000 年（22 年）得到的7 个空间模态夹角余弦绝对值均大于0.90（表略），表明这7 个温度模态具有很好的时间稳定性。这些模态表现为7 种不同的纬向和经向传播的东亚850 hPa 低频温度波列（其中图3a–d 分别给出了东亚850 hPa 25～40 d 低频温度场第1～4 空间模态），它们与东亚季风各种环流低频波列异常传播的关系密切，这些东亚地区大尺度低层温度波列是驱动冬季东亚各区域极端低温天气的主要低频系统。另外，上述7 个PC 与长江下游地区气温25～40 d 低频分量的相关系数分别是−0.18、−0.59、−0.28、−0.17、0.10、−0.03 和0.14，其中前4 个PC 对应相关均通过95%信度水平的显著性检验（考虑序列持续性的影响，当相关系数为0.16 时，其通过95%信度水平的显著性检验），其中与第2 模态的负相关最为显著（相关系数为−0.59，通过99%信度水平的显著性检验）。这4个与长江下游温度低频分量密切相关的850 hPa 低频温度模态是东亚地区热带内、外各种季风环流系统相互反馈和作用的结果，导致了欧亚中高纬地区和西太平洋副热带地区低频变化对冬季长江下游地区持续低温影响的复杂性。从图3a 和3b 可以发现，第1、2 模态的空间分布均表现为从欧亚中高纬向热带西太平洋传播的低频波列结构[类似于与长江下游地区气温与东亚850 hPa 温度的低频相关的低频波列（图2a）]，是影响长江下游地区冬季极端低温事件的重要低频系统（通过欧亚中高纬地区和热带太平洋地区环流的相互作用）。而第3、4 模态呈现东亚中纬度东西向传播的温度波列，主要与中高纬度大气内部动力过程有关。上述4 种不同的东亚850 hPa 温度ISO 型是驱动长江下游地区低温冰冻过程的主要低频系统（其变化具有多样性），也是冬季长江下游地区气温10～30 d 延伸期预测的可预报性重要来源。

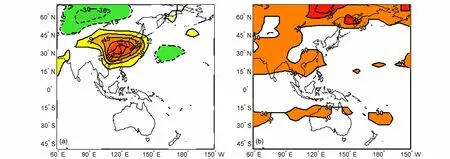
图2 （a）1979～2018 年长江下游地区25～40 d 低频气温与东亚850 hPa 25～40 d 低频温度的相关系数分布，图中相关系数值是原始值×100 后的结果，阴影表示通过95%信度水平显著性检验的区域；（b）850 hPa 低频温度场距平25～40 d 滤波序列与原始序列季节内方差比值的空间分布，图中数值是原始值×100 后的结果（单位：%），阴影区表示方差比值≥30 的区域Fig.2 (a) Correlation coefficients between the low-frequency air temperature over the LYR and 850-hPa low-frequency temperature in eastern Asia on the 25–40-day time scale from 1979 to 2018, in which values are multiplied by 100 and shadings indicate the correlation coefficients above 95%confidence level; (b) spatial distribution of ratio of the variance for the 850-hPa low-frequency temperature anomalies on the 25–40-day time scale to the total seasonal variability, in which values are multiplied by 100 and shadings indicate ratio of the variance greater than or equal to 30

此外，由于气候系统不同时间尺度的各种分量之间的非线性相互作用，长江下游25～40 d 温度低频分量与这4 个东亚850 hPa 温度主要低频分量之间的联系还存在年际变化[时间不稳定，可能与更长时间尺度（如60～90 d、90～180 d 和准2 年等）的低频环流背景变化有关]。图4a、b 和c 分别给出了2001 年7 月至2003 年6 月期间长江下游25～40 d 温度低频分量与东亚850 hPa 低频温度EOF 分析主要模态对应的时间系数PC1、PC2和PC3 之间365 天滑动相关的时间演变，图中显示出较明显的相关时段不规则的时间变化。与PC1 的滑动相关表现为2001 年和2003 年较稳定的负相关（图4a），但2002 年负相关显著减弱；与PC2 的滑动相关在2001 年7～8 月呈现负相关增强，并在2002～2003 年保持稳定的显著负相关（图4b）；但与PC3 的滑动相关在2003 年2～6 月显著负相关明显减弱，表现为较明显的相关不稳定（图4c）。另外，与PC4 的相关也显示类似的不规则时间变化（图略）。这种相关时间不稳定反映了在大气加热异常作用下（如海温、雪盖和土壤湿度等），东亚地区各种低频温度模态与长江下游低频温度相关存在较显著的年际变化。因此，构建预测模型时，考虑这种相关的时间变化信息是改进建模方案和提高预测精度的一个主要方面。另外，图5a、b 还给出了长江下游地区2001～2018 年期间逐日长江下游25～40 d 低频温度与基于T-EOF 延拓的SSA 滤波和无T-EOF 延拓的SSA 滤波25～40 d 低频温度的实时变化。从图中可以发现，基于T-EOF 延拓的SSA 滤波的实时温度低频信号（蓝色实线）变化精度明显优于经典SSA 滤波（无T-EOF 延拓）的实时信号[与真实的ISO 信号（对长序列的经典SSA 滤波，红色实线）的相关系数从0.606（图5b）提高到0.721（图5a）]，得到较高精度的用于低频模型预测的初始滤波值，更客观地反映观测数据中真实的ISO 强度和位相的实时变化。同时，对于东亚850 hPa 25～40 d 低频温度场的前4 个主成分PC1～4，用上述实时SSA 滤波提取这些850 hPa温度模态的实时温度低频主成分也得到类似的结果（图略）。因此，基于T-EOF 延拓的实时SSA 滤波的低频分量提取，对于准确反映实时低频分量之间的联系，提高预测模型低频分量初值精度和提高模型的预测性能十分重要。

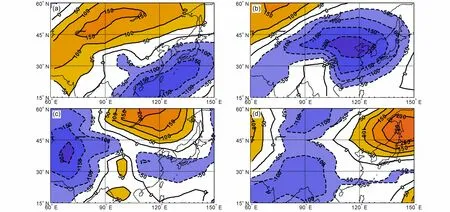
图3 1979～2000 年东亚850 hPa 25～40 d 低频温度场EOF 分解的（a–d）第1～4 空间模态，图中数值已乘以1000，实（虚）线表示正（负）值Fig.3 Principal spatial modes of the 850-hPa low-frequency temperature on the 25–40-day time scale in eastern Asia from 1979 to 2000, Figs. a–d correspond to modes 1–4 of EOF (empirical orthogonal functions). Values are multiplied by 1000, and the solid (dashed) lines represent positive(negative) values

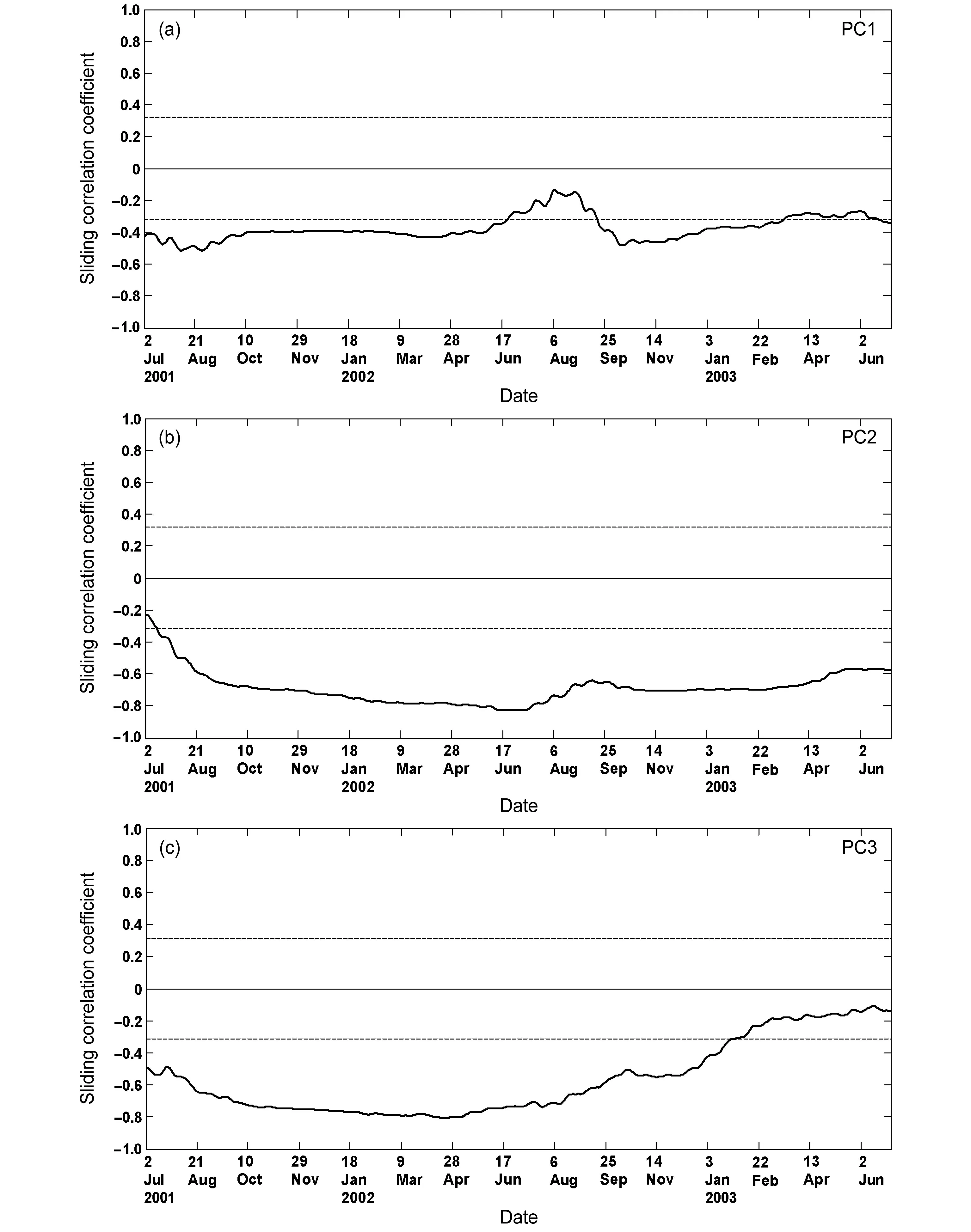
图4 2001～2003 年长江下游25～40 d 低频温度与东亚850 hPa 25～40 d 低频温度EOF 分析主要模态对应的时间系数的365 天滑动相关系数：（a）PC1；（b）PC2；（c）PC3。水平虚线表示95%信度水平Fig.4 Sliding correlation coefficients between the low-frequency temperature in the LYR and the principal components (PC) of 850-hPa lowfrequency temperature in eastern Asia on the 25–40-day time scale with a window length of 365 days during 2001–2003: (a) PC1; (b) PC2; (c) PC3.The horizontal dashed lines represent the 95% confidence level

5 预测试验

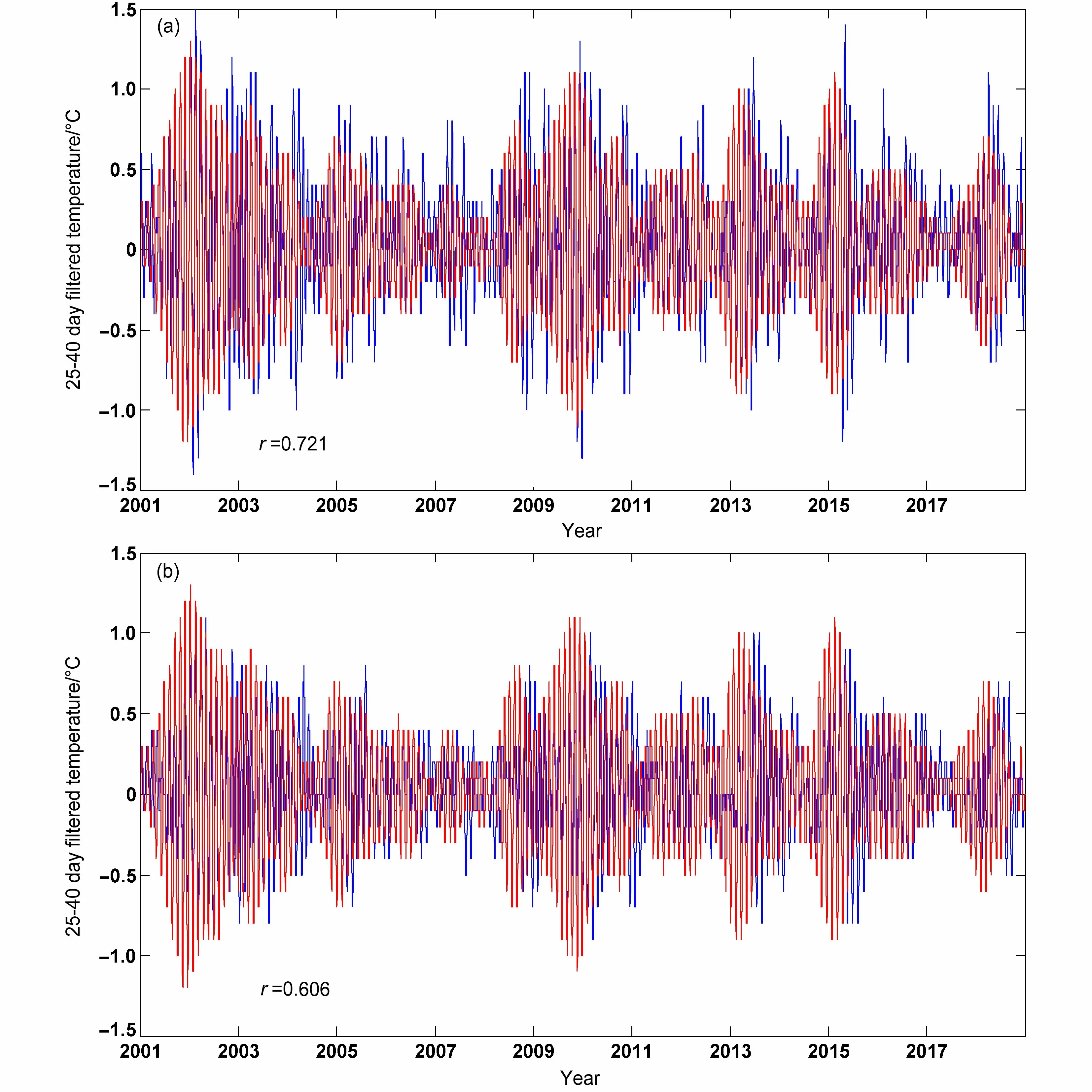
图5 2001～2018 年长江下游地区逐日25～40 d 低频温度（对长序列的经典SSA 滤波，红线）与（a）基于T-EOF 延拓的SSA 滤波和（b）无T-EOF 延拓的SSA 滤波的实时低频温度（蓝线）的变化。r 是它们之间的相关系数Fig.5 Time series of the 25–40-day low-frequency temperature [SSA (singular spectrum analysis) filtered, red lines] in the LYR and real lowfrequency temperature (blue lines) with the (a) T-EOF (temporal empirical orthogonal functions) extension and (b) without the T-EOF extension from 2001 to 2018. r indicates their correlation coefficients

本文用22 年（1979 年1 月1 日至2000 年12月31 日，8036 d）资料，得到长江下游地区逐日低频温度和东亚850 hPa 25～40 d 低频温度场的前4 个低频主成分，构建ECAR 模型对2001/2002～2017/2018 年 每 年12 月1 日 至 次 年2 月28 日（1530 d）的长江下游地区17 个冬季逐日低频温度进行历史回报试验。在这些回报试验中，用限定记忆法，建立时变ECAR 滑动进行独立样本预测试验[其中子序列长度M0=365 d，复自回归模型的阶数p=2，预报时间K=30 d（初始时间是2001/2002～2017/2018 年每年11 月1 日至次年2月27 日，预报未来30 d）]。以上建模方案有利于适应各个低频分量之间的相关随时间的改变（主要是低频相关的年际变化，图4a、b、c），还能适当地反映气候系统分量之间时滞相关的一些非预期的时间变化，提高预报模型的稳定性。

在独立预测试验中，首先将2001～2018 年逐日观测的东亚850 hPa 温度场投影到前L 个（L =4）25～40 d 低频空间分布型（由1979～2000 年的逐日数据计算），得到前L 个主成分的观测值；然后将这L 个观测的850 hPa 温度主成分和同期的长江下游逐日气温分别投影到各自经SSA 后的对应于25～40 d 振荡的T-EOF 上（由1979～2000 年的逐日数据计算850 hPa 温度主成分和长江下游地区气温各自的T-EOF），得到2001～2018 年期间的逐日850 hPa 温度的25～40 d 重构分量T1,T2,···,TL和长江下游地区气温重构分量 tlcj，构建扩展资料矩阵（F）：

图7a 给出了用限定记忆法（其中子序列长度M0=365 d），建立的时变ECAR 模型计算的2001/2002～2017/2018 年每年12～2 月（17 个冬季）长江下游地区逐日气温低频分量的未来30 d 预报与观测的相关系数（即相关预报技巧）。这些预测的初始时间分别是每年11 月1 日到次年2 月27 日，17 个冬季共2023 次预报。从图7a 中可以看出，冬季长江下游25～40 d 气温低频分量的预报时效达26 d（相关预报技巧大于0.5，通过95%信度水平的显著性检验，考虑序列持续性的影响）。另外，低频温度分量预报的均方根误差（Root-meansquare error, RMSE）也 在26～27 d 左 右 增 大 到1.0 σ（ σ:低频分量的标准差）以上（图7b）。这表明简化的时变ECAR 可以较好地预报未来3～4周冬季长江下游地区低频温度分量的变化。图8是2001/2002～2017/2018 年期间12～2 月的11 d、14 d、17 d 和20 d 预报技巧的年际变化，表明了大部分年份ECAR 的预报技巧在未来20 d 预报时效内呈现显著的正相关（预报技巧大于0.50），能较好地预测这些25～40 d 振荡活跃年份冬季长江下游低频温度的变化。仅2006/2007 年和2016/2017年冬季分别在14 d 和11 d 以后的预报技巧出现较明显降低，但相关预报技巧仍然达到0.25 左右，这2 年冬季是预报技巧偏低的时期。另外，直接用观测的长江下游温度低频分量建立自回归模型（AR）滑动进行独立样本预测试验，预报时效只有7 d 左右（图7a、b 中虚线），即预报技巧在1 周后迅速下降（子序列长度M0=365 d）。它表明AR模型预测稳定性明显减小，预报时效显著缩短（由于经典的AR 模型不能体现东亚地区冬季多种低频温度模态的协同作用）。

图6 时变ECAR 预测模式构建示意图。T850：实时东亚850 hPa 温度；T1，T2，T3，T4：实时东亚850 hPa 温度低频主成分（PC）； tlcj：实时长江下游低频温度；F：扩展资料矩阵， t0 ：初始时间； M0：子序列长度；TE1，TE2，TE3，TE4：1979 年1 月1 日至2000 年12 月31日25～40 d 东亚850 hPa 温度主要模态前4 个主模态V1，V2，V3，V4 的T-EOFs；TEt：1979 年1 月1 日至2000 年12 月31 日25～40 d 长江下游温度的T-EOFsFig.6 Schematic representation of the time-varying ECAR (Extended complex autoregressive) forecasting model. T850: Real-time 850-hPa temperature in eastern Asia; T1, T2, ···, T4: Real-time low-frequency principal components (PC) of the 850-hPa temperature in eastern Asia; tlcj: Realtime low-frequency temperature over the LYR; F: Extended data matrix; t0 : Initial time; M0: Length of the subsequence; TE1, TE2, ···, TE4: Respective T-EOFs (temporal empirical orthogonal functions) of the principal components of the 850-hPa temperature in eastern Asia on the 25–40-day time scale for the first fourth modes V1, V2, ···, V4 from 1 January 1979 to 31 December 2000; TEt: T-EOFs of the daily temperature over the LYR on the time scale of 25–40 days from 1 January 1979 to 31 December 2000

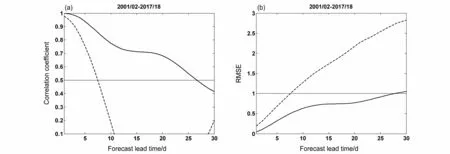
图7 2001/2002～2017/2018 年12～2 月长江下游温度低频分量1～30 d 预报与观测的（a）相关系数、（b）标准化均方根误差。实线：ECAR 模型；虚线：AR 模型。图a、b 中水平实线分别表示95%的信度水平和1 σ （ σ表示标准差）Fig.7 (a) Correlation coefficients and (b) RMSE (root-mean-square error) between the observation and the 1- to 30-day forecast for the lowfrequency temperature component over the LYR in December–February of 2001/2002–2017/2018. Solid line: ECAR model; dashed line: AR model.The horizontal solid lines in Fig.a and Fig.b represent the 95% confidence level and 1 σ( σindicates standard deviation), respectively

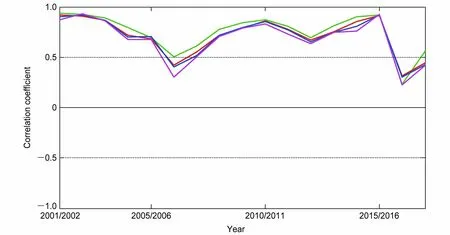
图8 2001/2002～2017/2018 年12～2 月长江下游温度低频分量预测和实况之间相关系数的年际变化。绿、红、蓝、紫线分别表示11 d、14 d、17 d 和20 d 预报，水平虚线表示95%信度水平Fig.8 Interannual variations of the correlation coefficient between the forecast and the observation of the low-frequency temperature component over the LYR in December–February during 2001/2002–2017/2018. The lead times are 11 days (green line), 14 days (red line), 17 days (blue line), and 20 days (purple line). The horizontal dashed lines represent the 95% confidence level

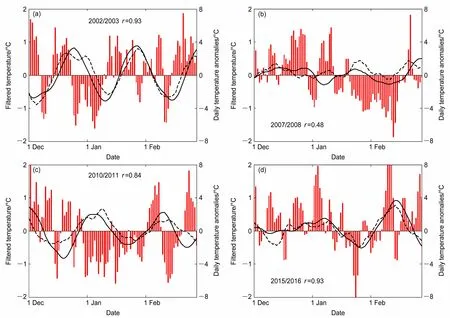
图9 （a）2002/2003 年、（b）2007/2008 年、（c）2010/2011 年、（d）2015/2016 年12～2 月长江下游地区25～40 d 温度低频分量的实况（实线）和ECAR 模型的20 d 预报（虚线）。柱状表示逐日气温距平（单位：°C），r 是预测和实况之间的相关系数，预报的初始时间分别是11 月11 日、11 月12 日……、2 月8 日Fig.9 Observation (solid lines) and forecast (dashed lines) of the ECAR model at a lead time of 20 days for the low-frequency temperature component over the LYR from December to February of (a) 2002/2003, (b) 2007/2008, (c) 2010/2011, and (d) 2015/2016. The bars represent the daily temperature anomalies (units: °C), r is the correlation coefficient between the forecast and the observation, the initial date of forecast is 11 November,12 November,..., 8 February, respectively

图9 进一步给出2002/2003 年、2007/2008 年、2010/2011 年和2015/2016 年冬季的长江下游逐日低频温度分量20 d 预报和观测的逐日变化曲线，其中25～40 d 振荡较强的2002/2003 年（图9a），2010/2011 年（图9c）和2015/2016 年（图9d）的相关预报技巧分别达到0.93、0.84 和0.93（每个冬季的90 次预报，初始时间分别是11 月11 日、11月12 日、…、2 月8 日），其显著性水平为0.01（考虑序列持续性的影响）。从图中可以看出，ECAR 能较准确地预测上述年份中长江下游12～2月的2～3 个主要持续低温集中期对应的显著低频温度负位相变化和低温期，尤其是与2002 年12 月下旬和2003 年2 月中旬（图9a）、2011 年2 月上旬末到中旬（图9c）和2016 年1 月下旬（图9d）的4 次负温度距平伴随的持续低温过程对应的低频温度分量位相变化（正的峰值位相转负位相过程，即低频升温向低频降温的位相转换）能较好地预测，其预报的负位相变化与实况基本一致。但是2008 年1 月下旬到2 月中旬前期长江下游较长时间的持续温度负距平（持续28 d），与更长时间尺度的70 d左右的低频振荡有关（图1a）。ECAR 模型仅预测出与1 月中旬和2 月上旬持续负温度距平对应的较弱的25～40 d 振荡低频正负位相变化（图9b），需要进一步构建时间尺度是70 d 左右的低频温度分量预测模型进行预测，才能提高这种由多个周期的低频振荡共同作用产生的长江下游持续4 周左右的持续低温冰冻过程的预报能力。此外，2016/2017 年的20 d 预报技巧明显下降（图8），主要原因是这一年冬季25～40 d 振荡较弱，月内主要强振荡周期大约在13 d 左右（图1a），所以25～40 d 低频振荡的ECAR 预测模型出现一些不稳定。类似地，2006/2007 年主要强低频振荡周期是20 d左右（图1a），冬季25～40 d 振荡不显著，ECAR模型的预测技巧下降（预报时效小于14 d，图8）。以上大量独立预报试验表明，简化的ECAR 模型能有效描述这17 个冬季中的大部分冬季（25～40 d振荡活跃的冬季）主要低频温度分量之间多种时滞相关变化信息，同时也包含一些非预期的相关信息，所以能比较精确地预测这些低频变化。因此，这种数据驱动的ECAR（LFCF2.0），基于SSA，从观测的时间序列的动力重构出发，滤去序列中的高频噪声，能精确地提取东亚850 hPa 温度和长江下游地区气温中的主要低频模态的非均匀的时间变化分量；在实时预报中，由于实时SSA 滤波明显减弱了经典SSA 滤波的边界效应，得到的观测数据中真实的ISO 信号明显增强，从而使得实时分量的重建序列分别成为单一和稳定的具有不同周期的主要低频信号序列，随机干扰得到了有效的衰减，显著增强了可预报性。然后基于主要复数低频分量的协同演化过程（通过数据变换生成复数空间中的虚拟数据，扩展有效数据规模），由数据驱动构建能描述更多大气低频分量相互作用过程的简化复数自回归预测模型（杨秋明，2014b），可以将长江下游地区冬季低温冰冻时段的预报时效延长到3～4 周。

ECAR 预测方法基于实数据和虚数据之间的协同演化新规律，在一定程度上，突破了物理世界资源有限的约束，可以更有效地描述气候系统中主要低频模态时空变化的多样性（杨秋明, 2014b）。通过适当的数据变换，减少预测的不确定性、将多样化为归一、使复杂变简单。上述基于长序列历史数据的独立预报试验表明，与长江下游冬季低温密切相关的25～40 d 温度低频分量的时变ECAR 模型的预报时效可达26 d 左右，大于与夏季长江下游高温密切相关的30～60 d 低频温度的23 d 的预报时效（杨秋明, 2018）。它表明简化的时变ECAR模型均能有效预报冬季和夏季不同时间尺度的温度ISO 分量未来3～4 周的变化，其中冬季的预报时效更长。ECAR 模型在大于3 周的预报时效中具有很好的温度低频分量预报稳定性，能为长江下游地区极端温度变化过程的实时延伸期预测提供较可靠的预报信息，但这些不同时间尺度的温度ISO型强度的季节和年际变化机制是需要进一步研究的问题。详细揭示缓变下垫面各种外强迫调控大气次季节变化过程的机理，更好地综合考虑热带低纬度和两半球中高纬度的不同低频信息的作用，将是提高东亚冬季风ISO 预测时间上限的关键。同时基于长江下游地区冬季低温日数与一定周期ISO 的稳定的关系及其相关的年际变化，进一步改进数据分析方法，更精确地提取实时ISO 信号，构建时变简化数据模型可以进一步延长冬季10～30 d 延伸期极端气候事件的预报时效并提高月温度距平气候预测精度。另外，数据驱动的低频信号提取和构建ECAR 模型方法也可以广泛应用于年际变化分量（如准2 年振荡，3～4 年振荡等）和年代际变化分量（如20～30 年振荡等）的预测。进一步综合次季节、年际和年代际变化信息，全方位实时监测不同时间尺度低频信号的变化，对关键数据进行多层次多角度的分析，构建这种实时简化气候预测模型，更好地反映气候系统中多时间尺度的相互作用，可以显著提高气候预测的整体水平。

6 结论和讨论

本文基于1979～2018 年逐日长序列资料，研究了39 年冬季（1979/1980～2017/2018 年）长江下游地区气温主要季节内变化周期与12～2 月低温日数的联系，同时研究主要气温低频分量与东亚主要的850 hPa 温度模态变化的关系。采用SSA，从观测数据中提取东亚地区850 hPa 温度和长江下游冬季气温和主要低频分量（季节内时间尺度），通过Fourier 变换生成的复低频分量组成扩展复数据阵,构建时变扩展复数自回归模型（ECAR）（即LFCF2.0），对冬季长江下游地区低频温度分量进行延伸期预报试验并研究可预报性的年际变化，得到以下结论：

（1）冬季长江下游逐日气温存在较显著的季节内振荡周期（15～25 d、25～40 d 和50～70d 振荡），其中与12～2 月低温日数关系最密切的是25～40d 振荡。这种25～40 d 振荡与东亚热带外850 hPa 温度前4 个主要25～40 d 低频模态的变化密切相关，其中最相关的是第2 模态（EUP 波列），但与热带西太平洋地区ISO 的变化的联系不显著。它反映了冬季欧亚中高纬度地区大气加热异常和大气内部动力过程产生的各种低频模态变化对长江下游地区冬季气温低频变化的影响，这些东亚低层25～40 d 温度波列是驱动冬季长江下游地区极端低温天气的主要低频系统。

（2）基于1979～2000 年长江下游地区逐日温度和东亚850 hPa 温度场25～40 d 低频主要模态，通过Fourier 变换，在复空间上构建的时变ECAR预报模型（LFCF2.0）能较好地预测2001/2002～2017/2018 年12～2 月长江下游逐日气温25～40 d低频分量未来26 d 左右的变化，可以提前3～4 周左右预测冬季长江下游持续低温事件，能为长江下游地区冬季低温冰冻过程（对应于25～40 d ISO变化）的实时延伸期预报提供稳定的预报信号。但是，用经典AR 模型预测低频温度分量的预报时效仅7 d 左右，预报时效明显缩短。因此，基于复空间包含更多低频信号构建的复数自回归模型预测技巧显著高于原始实空间低频分量自回归模型。

（3）长江下游地区冬季气温25～40 d 振荡活跃的年份，其低频分量的ECAR 模型预报时效较长（大于25 d）。但在25～40 d 振荡较弱的年份（2006/2007 年和2016/2017 年）预报技巧显著减小，这时振荡周期较短的10～20 d 振荡或较长的50～70 d 振荡可能起主导作用，可以选择相应的关键区域的温度低频主成分构建对应的ECAR 模型预测它们未来30 d 的变化，由预测的低频分量的位相变化估计长江下游地区冬季持续低温时段。

大量气象观测资料具有高度数据相关性和多重数据属性，反映和表征着复杂的自然现象与关系。本文对长序列观测数据进行变换和分解，提取长江下游地区冬季气温低频变化和东亚中高纬度和副热带地区850 hPa 温度主要低频模态对应的低频主成分，分析这些低频分量之间的联系，并将这些主要低频分量视为气候数据多样化演变过程的主要数据解，通过Fourier 变换生成的复低频分量，反演出可预报性较大的简化的时变复数据模型ECAR。这种预报方法显著减小了计算误差，较好地反映主要低频分量之间的相互作用，并延长了预报时效。这些数据驱动的气候预测方法不受数值预报时效的可预报性限制,不预设各种物理条件。同时，基于TEOF 延拓的实时SSA 滤波，可以很好地抑制滤波边界效应得到稳定的实时ISO 信号。这种实时SSA 滤波能快速、精准反映观测数据中实时ISO信号的位相和强度变化，更全面反映复杂气候系统自然变化信息。进一步优化各种数据分析方法，更好地整合数据的力量，基于实数据和虚数据之间的协同变化过程，可以建立预测稳定性更好的各种简化数据模型，让预报模式从根本上摆脱可预报性的束缚，实现模式的1～10 d 短中期和10～30 d 延伸期以及短期气候无缝隙预报的能力。